что такое равенство треугольников

Треугольник. Признаки равенства треугольников.

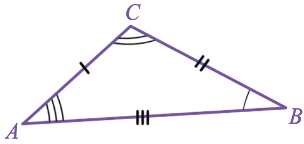
Треугольник – геометрическая фигура, сформированная тремя отрезками, которые соединяют три точки, не принадлежащие одной прямой.

Стороны треугольника формируют в вершинах треугольника три угла. Перефразируя, треугольник – это многоугольник, у которого три угла.

Практическое значение признаков равенства треугольников сводится к нижеследующему: согласно формулировке треугольники равны, в случае когда получается их наложить друг на друга так, чтобы они совпали; однако реализовать наложение треугольников иногда бывает трудно, а иногда и невозможно.

Признаки равенства треугольников позволяют заменить наложение треугольников нахождением и сопоставлением отдельных основополагающих компонентов (сторон и углов) и таким образом обосновать равенство треугольников.

У равных треугольников тождественны и их соответствующие элементы.

И так треугольники равны, если у них соответственно равны:

1. Две стороны и угол между ними:

2. Сторона и прилежащие к ней два угла:

Еще выделяют четвертый признак, который не так широко освещен в школьном курсе математики как предыдущие три. Он формулируется следующим образом:

Если две стороны первого треугольника соответственно равны двум сторонам второго треугольника и угол, противолежащий большей из этих сторон в первом треугольнике, равен углу, противолежащему соответственно равной ей стороне во втором треугольнике, то эти треугольники равны.

Источник

Что такое равенство треугольников

Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.

Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.

Медиана, биссектриса и высота треугольника

Равные треугольники

Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.

Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.

Признаки равенства треугольников

Дополнительные признаки равенства
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.

Это конспект по теме «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:

Источник

Признаки равенства треугольников

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

Равенство треугольников

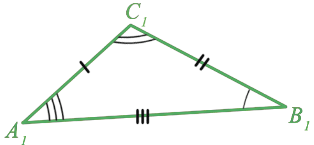
Мы знаем, что две геометрические фигуры считаются равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы, значит, если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

Пример:

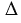
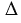
Равенство треугольников ABC и A₁B₁C₁ обозначается так: ABC = A₁B₁C₁

В равных треугольниках против соответственно равных сторон лежат равные углы и обратно: против соответственно равных углов лежат равные стороны.

Для примера рассмотрим одну из пар сторон треугольников: BC = B₁C₁, значит, 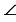A = A₁ и наоборот: из того что A = A₁, следует, что BC = B₁C₁.

Поделись с друзьями в социальных сетях:

Источник

Геометрия. 7 класс

Конспект урока

Повторение. Треугольник. Равенство треугольников

Перечень вопросов, рассматриваемых в теме:

Треугольник – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Сумма углов треугольника равна 180°.

Признаки равенства треугольников.

1 признак. Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2 признак. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3 признак. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Теоретический материал для самостоятельного изучения

Треугольник – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

В любом треугольнике:

Два треугольника называются равными, если их можно совместить наложением.

На рисунке изображены равные треугольники ABC и А₁В₁С₁. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины, стороны и углы.

Первый признак равенства треугольников:

По двум сторонам и угол между ними.

Второй признак равенства треугольников:

По стороне и двум прилежащим к ней углам.

Третий признак равенства треугольников:

Признаки равенства прямоугольных треугольников.

Свойства прямоугольных треугольников.

Разбор решения заданий тренировочного модуля.

Решение задач по теме: «Прямоугольный треугольник».

Дано: ∠C = 44°.Найдите: ∠ABD.

Помним, что сумма острых углов равна 90°. Равные углы отмечены на рисунке. ∠ABD = 44°.

Дано: AB = 6. Найдите: AC.

Указания к решению: помним, что против угла 30° лежит катет, равный половине гипотенузы. На рисунке найдите три треугольника, в каждом из которых, есть угол 30°.

В треугольнике ABC против угла С = 30°, лежит катет AB = ½AC. Значит, AC = 12.

Задача 3. В ∆АВС: ∠А = 30°, ∠В = 80°. Биссектрисы углов А и С пересекаются в точке О. Найти величину ∠АОВ.

Сумма углов А и В равна 110°. Сумма их половинок равна 55°. Тогда: ∠АОВ = 180° – 55° = 125°.

Может ли существовать треугольник со сторонами: 14 см, 17 см, 10 см?

Источник