что такое процентиль в статистике
Процентили
— это характеристики набора данных, которые выражают ранги элементов массива в виде чисел от 1 до 100, и являются показателем того, какой процент значений находится ниже определенного уровня.
Например, значение 30-й процентили указывает, что 30% значений располагается ниже этого уровня.
На конкретном примере поясним понятие процентиля:
Решение.
Формула процентиля
Процентиль = n(x≤X)/N*100
Для удобства вычислений ранжируем выборку балов от максимального значения до минимального ( в порядке убывания): 5,5,5,4,4,4,4,4,4,4,4,3,3,3,3,3,3,2,2,2
Допустим нам необходимо определить процентиль студента Иванова получившего на экзамене 5 баллов:
Процентиль (Иванова) = 20/20*100=100
Допустим необходимо определить процентиль студента Петрова получившего на экзамене 4 балла:
Процентиль (Петрова) = 17/20*100=85
Допустим необходимо определить процентиль студента Сидорова получившего на экзамене 3 балла:
Процентиль (Иванова) = 9/20*100=45
После расчета процентиля можно составить таблицу стандартизации. Для наших баллов она будет выглядеть следующим образом:
| Бал | Процентили |
| 5 | 100 |
| 4 | 85 |
| 3 | 45 |
| 2 | 15 |
Алгоритм расчета процентилей
1. Для каждого человека посчитать, какое количество человек набрало столько же или меньше баллов.
2. Посчитать сколько процентов составляет это количество от всей выборки.
Процентиль – это процент людей из выборки, набравших столько же или меньше баллов, чем конкретный человек.
Процентиль является достаточно распространенной шкалой стандартизации, среди психологов, социологов, биологов, медиков и т.д., т.к. очень удобен и понятен. Его диапазон от 1 до 100.
Процентили указывают на относительное положение индивида в выборке стандартизации. Их также можно рассматривать, как ранговые градации, общее число которых равно 100, с той лишь разницей, что при ранжировании принято начинать отсчет сверху, т.е. с лучшего члена группы, получающего ранг 1. В случае же процентилей отсчет ведется снизу, поэтому, чем ниже процентиль, тем хуже позиция индивида.
Процентиль может использоваться для стандартизации как нормально распределенных случайных величин СВ, так и данных с ненормальным распределением.
Расчет процентилей в Excel
Для расчета процентилей нам понадобится функция СЧЕТЕСЛИ.
Для расчета, для каждого значения нужно ввести формулу:
Описательные статистики
Упорядочим эти величины по возрастанию, иными словами, построим вариационный ряд:
Х(1) x более важны, чем другие. Мы присоединяем вес wi к каждому из значений xi в нашей выборке для того, чтобы учесть эту важность.
Например, предположим, что мы заинтересованы в определении средней продолжительности госпитализации в каком-либо районе и знаем средний реабилитационный период больных в каждой больнице. Учитываем количество информации, в первом приближении принимая за вес каждого наблюдения число больных в больнице.
Взвешенное среднее и среднее арифметическое идентичны, если каждый вес равен единице.
Размах (интервал изменения)
Размах — это разность между максимальным и минимальным значениями переменной в наборе данных; этими двумя величинами обозначают их разность. Обратите внимание, что размах вводит в заблуждение, если одно из значений есть выброс (см. раздел 3).
Размах, полученный из процентилей
Что такое процентили
Предположим, что мы расположим наши данные упорядоченно от самой маленькой величины переменной X и до самой большой величины. Величина X, до которой расположен 1% наблюдений (и выше которой расположены 99% наблюдений), называется первым процентилем.
Величина X, до которой находится 2% наблюдений, называется 2-м процентилем, и т. д.
Применение процентилей
Мы можем добиться такой формы описания рассеяния, на которую не повлияет выброс (аномальное значение), исключая экстремальные величины и определяя размах остающихся наблюдений.
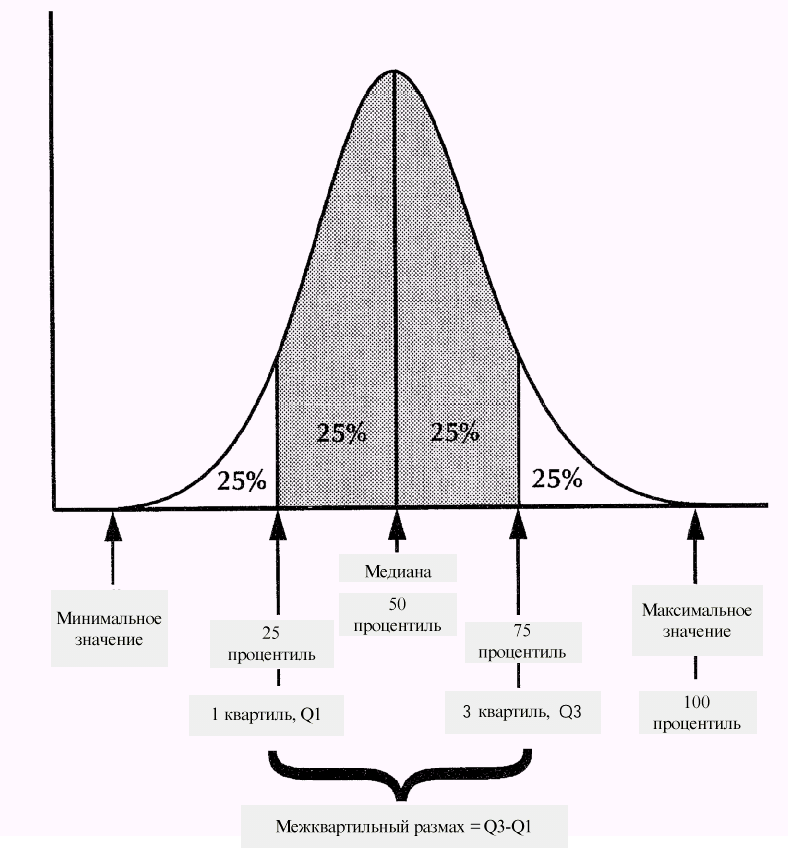
Межквартильный размах — это разница между 1-м и 3-м квартилями, т.е. между 25-м и 75-м процентилями. В него входят центральные 50% наблюдений в упорядоченном наборе, где 25% наблюдений находятся ниже центральной точки и 25% — выше.
Интердецильный размах содержит в себе центральные 80% наблюдений, т. е. те наблюдения, которые располагаются между 10-м и 90-м процентилями.
Мы часто используем размах, который содержит 95% наблюдений, т.е. он исключает 2,5% наблюдений снизу и 2,5% сверху. Указание такого интервала актуально, например, для осуществления диагностики болезни. Такой интервал называется референтный интервал, референтный размах или нормальный размах.
Дисперсия
Один из способов измерения рассеяния данных заключается в том, чтобы определить степень отклонения каждого наблюдения от средней арифметической. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений.
Однако мы не можем использовать среднее этих отклонений как меру рассеяния, потому что положительные отклонения компенсируют отрицательные отклонения (их сумма равна нулю). Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений; эта величина называется вариацией, или дисперсией.
В случае, если мы имеем дело не с генеральной совокупностью, а с выборкой, то вычисляется выборочная дисперсия:
Теоретически можно показать, что получится более точная дисперсия по выборке, если разделить не на n, а на (n-1).
Единицы измерения (размерность) вариации — это квадрат единиц измерения первоначальных наблюдений.
Например, если измерения производятся в килограммах, то единица измерения вариации будет килограмм в квадрате.
Среднеквадратическое отклонение, стандартное отклонение выборки
Среднеквадратическое отклонение — это положительный квадратный корень из дисперсии.
Мы можем представить себе стандартное отклонение как своего рода среднее отклонение наблюдений от среднего. Оно вычисляется в тех же единицах (размерностях), что и исходные данные.
Если разделить стандартное отклонение на среднее арифметическое и выразить результат в процентах, получится коэффициент вариации.
Он является мерой рассеяния, не зависит от единиц измерения (безразмерный), но имеет некоторые теоретические неудобства и поэтому не очень одобряется статистиками.
Вариация в пределах субъектов и между субъектами
Если провести повторные измерения непрерывной переменной у исследуемого объекта, то можно увидеть ее изменения (внутрисубъектные изменения). Это можно объяснить тем, что объект не всегда может дать точные и те же самые ответы, и/или ошибкой, погрешностью измерения. Однако при измерениях у одного объекта вариация обычно меньше, чем вариация единичного измерения в группе (межсубъектные изменения).
Например, вместимость легкого 17-летнего мальчика составляет от 3,60 до 3,87 л, когда измерения повторяются не менее 10 раз; если провести однократное измерение у 10 мальчиков того же возраста, то объем будет между 2,98 и 4,33 л. Эти концепции важны в плане исследования.
Что такое процентиль?
Что такое процентиль?
Термин ″процентиль″ (percentile) часто встречается в зарубежной литературе про инвестиции и вообще в статистических исследованиях – одно из таких исследований я упоминал в этой статье. Другими вариантами русских названий являются ″персентиль″ и ″перцентиль″. Думаю, что небольшая известность термина в России не вполне заслужена, поскольку нередко именно в процентилях удобно выразить полученные результаты.
Процентиль это определенная часть выборки данных
Возьмем простой пример. Группа студентов из 200 человек пишет тест, состоящий из 100 вопросов. Проходной порог, когда тест считается сданным, составляет 2/3 правильных ответов, т.е. не менее 66. Что получается с точки зрения отдельного студента?
Допустим, Иван правильно ответил на 70 вопросов. Задачу он выполнил — тест засчитан. Результат каждого участника теста также сравнивается с числом 66: если правильных ответов больше, тест сдан. В результате формируется список сдавших и не сдавших: каждый студент проходил через это. Пока ничего нового.
Но задачу можно поставить и по-другому: нужно сравнить результаты студентов не с проходным баллом в 66 пунктов, а между собой. Зачем это нужно? В данном случае, например, для объективной оценки сложность теста, что достигается группировкой результатов.
Вернемся к Ивану, который получил 70 правильных ответов. Много это или мало по сравнению с остальными? Это и покажет процентиль.
Процентили делят всю выборку на определенные части. Например, пятый процентиль охватывает 5% объема выборки. Предположим, показатель Ивана равен пятому процентилю. Это означает, что Иван написал тест лучше, чем 5% студентов (10 человек из 200 получили от нуля до 70 баллов). Не густо, поскольку в этом случае остальные 190 человек набрали больше, чем 70. Значит, тест был очень легкий и порог в 66 баллов можно и повысить.
Но в том же самом тесте может быть и обратная ситуация: результат Ивана равен 90-ому процентилю. Это значит, что Иван написал тест лучше, чем 90% студентов. Или по другому: только 10% (20 человек) набрали более 70 правильных ответов. Следовательно, тест был весьма трудным. Преимущество метода еще и в том, что разбивкой на процентили можно сравнивать тесты с разным числом участников.
Функция Гаусса
Чем более высок процентиль, тем больше данных он включает
Расчет процентиля в Excel
Процентиль несложно вычислить по формуле:
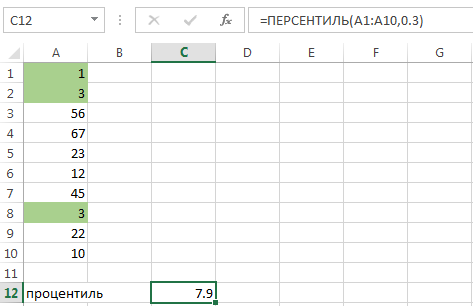
но проще обрабатывать массив данных одноименной функцией Excel. Для примера возьмем произвольную выборку полученных баллов и рассчитаем в ней процентили:
Функция PERCENTILE (ПЕРСЕНТИЛЬ) включает в себя ввод диапазона ячеек данных (А1:А10) и значения процентиля К, деленного на 100%. Т.е. в данном случае ввод 0.3 означает нахождение тридцатого процентиля. Смысл расчета: к 30-му процентилю будут относиться все результаты, меньше или равные 7.9.
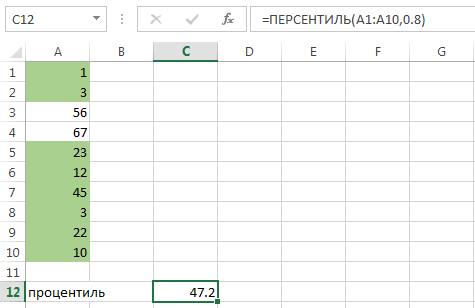
Если мы хотим узнать процентиль участника, получившего 10 баллов, то это несложно сделать, варьируя значение К до тех пор, пока значение в ячейке С12 не станет близким 10. Получится примерно 34-ый процентиль. При увеличении процентиля в выборку попадает больше табличных значений:
Итого, в 80-ый процентиль попадает уже 8 табличных значений из 10, которые меньше или равны 47.2. При этом подчеркнуть результат можно диапазоном процентилей — например, между восьмидесятым и сотым. В этом случае значения будут лежать между 47.2 и 67 (максимальным числом выборки).
Процентиль, Процентиль и Процентиль: Определение и примеры
Статистика Определения > Проценты, Процентный рейтинг и Процентный диапазон
Как найти процентиль
Что такое “Процентиль”?
“Процентиль” используется в обычном употреблении, однако для него нет определения “все включено”. Самое распространенное значение перцентиля – это когда конкретный уровень баллов падает ниже этого числа. Вы можете понять, что вы набрали 67 баллов из 90 на тесте. В любом случае, эта цифра не имеет никакого значения, за исключением того, что вы узнаете, в какой перцентиль вы попадаете. Если вы осознаете, что ваш результат находится на 90-м процентиле, это означает, что вы набрали более высокий балл по сравнению с 90 процентилями тех, кто прошел тест.
Процентили, как правило, используются для отчета о результатах тестов, похожих на SAT, GRE и LSAT. Например, 70-ый процентиль на GRE 2013 года был 156. Это означает, что, если вы набрали 156 баллов в тесте, то ваш результат был выше, чем у 70 процентов испытуемых.
25-й процентиль дополнительно называется первичным квартилем.
Пятидесятым процентилем обычно является средний (в случае, если вы используете третье определение – см. ниже).
75-й процентиль также называется третьим квартилем.
Контраст между третьим и первым квартилем – это межквартильный пробег.
2. Процентное ранжирование
“Процентиль” случайно используется в вышеуказанном определении. Подобным образом использование “процентиля” обычно показывает, что под этим процентилем находится конкретная ставка. Например, если вы набрали 25-й процентиль, то в этот момент 25% участников теста находятся под вашим показателем. 25″ называется процентилем. При измерениях он может быть несколько более запутанным, так как на самом деле существует три значения “процентиля”. Вот первые два (см. ниже определение 3), в свете субъективного “25-го процентиля”:
Определение 1: “n-й процентиль” – это самый минимальный показатель, который является более значимым, чем конкретный показатель (“n”). В этой модели наше n – 25, поэтому мы ищем самую минимальную оценку, которая более заметна, чем 25%.
Определение 2: n-й процентиль – это самая маленькая оценка, которая более заметна, чем определенный уровень баллов, или эквивалентна ему. Чтобы переосмыслить это настоящее, это уровень информации, который падает на или ниже определенного восприятия. Именно это определение используется при оценке ПД. В этой модели 25-й процентиль – это показатель, который является более примечательным или эквивалентным 25 процентилям баллов.
Может показаться, что они в основном те же самые, но в то же время они могут вызвать огромные контрасты в результатах, несмотря на то, что они оба находятся на 25-м процентиле. Возьмите сопровождающий список тестовых баллов, запрошенных по рангу:
| SCORE | RANK |
| 30 | 1 |
| 33 | 2 |
| 43 | 3 |
| 53 | 4 |
| 56 | 5 |
| 67 | 6 |
| 68 | 7 |
| 72 | 8 |
3. Наиболее эффективный метод Открытия Процентиля
Тестовый вопрос: Узнайте, где 25-й процентиль находится в приведенном выше обзоре.
Этап 1: Узнайте, какое место занимает 25-й процентиль. Используйте прилагаемый рецепт:
Звание = Процентиль/100 * (количество вещей + 1)
Звание = 25/100 * (8 + 1) = 0.25 * 9 = 2.25.
Позиция 2.25 находится на 25 процентиле. Как бы то ни было, позиции 2.25 точно не существует (в любой момент известной о среднем школьном звании 2.25? Я не знаю!), поэтому вы должны либо собраться вместе, либо округлить вниз. Так как 2.25 ближе к 2, чем 3, я приспосабливаюсь к позиции 2.
Этап 2: Выберите определение 1 или 2:
Определение 1: Самый минимальный балл заслуживает большего внимания, чем 25% баллов. Это эквивалентно 43 баллам (позиция 3).
Определение 2: Самая маленькая оценка, которая заслуживает большего внимания, чем 25% баллов, или эквивалентна им. Это эквивалентно 33 баллам (позиция 2).
В зависимости от того, какое определение вы используете, 25-й процентиль может быть равен 33 или 43! Третье определение пытается устранить эту возможную ошибку:
Определение 3: Средневзвешенное значение перцентилей из двух первоначальных определений.
В вышеприведенной модели приведены средства, с помощью которых можно было бы рассчитать процентиль с использованием средневзвешенного значения:
Дублировать контраст между баллами на 0,25 (часть ранга, которую мы определили ранее). Баллы были 43 и 33, что дает нам различие в 10:
Добавьте результат к более низкому баллу. 2.5 + 33 = 35.5
Для этой ситуации 25-й процентиль равен 35,5, что сулит нам хорошие результаты, как и в 43 и 33.
По большому счету, процентиль – это, как правило, определение №1. Тем не менее, есть смысл обратить внимание на то, что любые измерения перцентилей производятся с использованием этого первого определения.
4. Процентный диапазон
Процентный диапазон – это контраст между двумя определенными перцентилями. гипотетически это могут быть любые два перцентиля, но наиболее известным является диапазон 10-90 перцентилей. Чтобы определить местонахождение пробега 10-90 процентилей:
Определите десятый процентиль, используя вышеуказанные достижения.
Рассчитайте 90-ый процентиль, используя вышеуказанные достижения.
Вычитайте 1-й этап (десятый процентиль) из 2-го этапа (90-ый процентиль).
Статистика — это грамматика науки о данных. Часть 3
Mar 30, 2019 · 4 min read
Повторение статистики для начала путешествия по науке о данных
Меры расположения
Процентили
Процентили делят упорядоченные данные на сто равных частей. В рассортированных данных процентиль — это точка, показывающая процентное отношение значений в наборе данных, находящихся ниже данной точки.
50-й процентиль — это медиана.
Например, на графике ниже показано развитие ребенка от рождения до 2 лет. Получается, что 98% развития ребенка за первый год жизни составляет в весе меньше 11,5 кг.
Другим примером является ра с пределение доходов в стране. 99-й процентиль — это уровень дохода, при котором 99% населения зарабатывают меньше этого значения и 1% — больше. Так в Великобритании, как показано на графике ниже, 99-й процентиль составляет 75.000 фунтов стерлингов.
Квартили
Квартили — это процентили, которые делят набор данных на четверти. Первый квартиль, Q1, равен 25-ому процентилю, третий квартиль, Q3, равен 75-ому процентилю. Медиана может быть обозначена либо вторым квартилем, Q2, либо 50-ым процентилем.
Интерквартильный размах (IQR)
IQR — число, которое показывает разброс средней половины (т.е. средние 50%) набора данных и помогает определить выбросы. IQR — это разница между Q3 и Q1.
Выбросы — это, проще говоря, те значения данных, которые находятся за пределами следующих интервалов: Q1–1.5 x IQR и Q3 + 1.5 x IQR.
Диаграмма «ящик с усами»
Диаграмма «ящик с усами» показывает:
Ящик с усами имеет горизонтальную и вертикальную оси и прямоугольный ящик.
«Усы» (выделенные фиолетовым цветом) начинаются с концов ящика и заканчиваются на самом минимальном или максимальном значениях данных. Также бывают ящики с усами, у которых есть отмеченные значения выбросов (выделены красным цветом). В таких случаях, усы не достигают минимального и максимального значений.
Ящики с усами на графике нормального распределения Ящики с усами на нормальных распределениях имеют некоторые особенности: Несмотря на то, что первый и третий квартили (Q1 и Q3) имеют такие названия, они, на самом деле, не составляют 25% от числа данных! Они показывают 34,135%. Также второй квартиль (Q2) составляет не 50%, а 68,27%.
Моменты случайной величины
Моменты случайно величины описывают различные аспекты характера и формы нашего распределения.
#1 — первый момент случайной величины — среднее значение данных, которое показывает место распределения.
#2 — второй момент случайной величины — дисперсия, которая показывает разброс распределения. Большие значения имеют больший размах, чем маленькие.
#3 — третий момент случайной величины — коэффициент асимметрии — мера того, насколько неравномерным является распределение. Коэффициент асимметрии положителен, если распределение наклонено влево и левый хвост короче правого. То есть среднее значение находится правее. И наоборот:
#4 — четвертый момент случайной величины — коэффициент эксцесса, который описывает то, насколько толстый хвост и насколько острый пик распределения. Этот коэффициент показывает, насколько вероятно найти точки экстремума в данных. Чем выше значение, тем вероятнее выбросы. Это похоже на разброс (дисперсию), но между ними есть отличия.
Как видно на графике, чем выше значение пики, тем выше коэффициент эксцесса, т.е. у верхней кривой коэффициент эксцесса выше, чем у нижней.