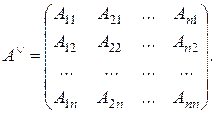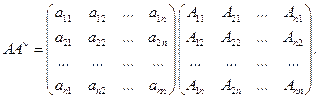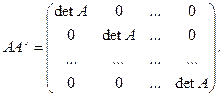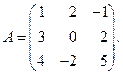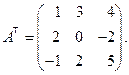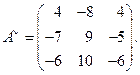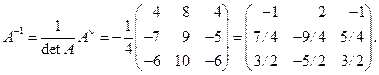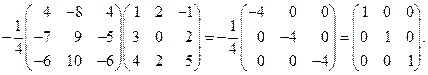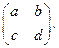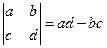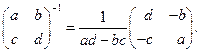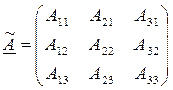Что такое присоединенная матрица

Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.

Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.

Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.

Метод присоединённой (союзной) матрицы

Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.

Итак, обратная матрица найдена:

$$A^<-1>=\left( \begin -8/103 & 7/103\\ 9/103 & 5/103 \end\right).$$

Составляем матрицу из алгебраических дополнений и транспонируем её:

Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.

Например, для первой строки получим:

А далее продолжаем находить алгебраические дополнения:

Матрица из алгебраических дополнений:

Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.

Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

Обратная матрица

Содержание

Обратимость в алгебре [ править ]

[math]xz=e, \ x[/math] — левый обратный

[math]zy=e, \ y[/math] — правый обратный.

Факт 2. Пусть [math]\exists z^<-1>, \ \tilde^<-1>[/math]

Критерий обратимости матрицы [ править ]

Предположим [math]\exists C: CA=E \Rightarrow \sum\limits_^ \gamma_^\alpha_^=\delta_^[/math]

Свойства обратной матрицы [ править ]

Методы нахождения обратной матрицы [ править ]

Метод Гаусса для нахождения обратной матрицы [ править ]

Пример [ править ]

Найдем обратную матрицу для матрицы

Метод присоединенной матрицы [ править ]

Алгебраическим дополнением элемента [math]\ a_[/math] матрицы [math]\ A[/math] называется число

[math]M_ = det\begin a_ <11>& a_ <12>& \cdots & a_ <1(j-1)>& a_ <1(j+1)>& \cdots & a_ <1n>\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_ <(i-1)1>& a_ <(i-1)2>& \cdots & a_ <(i-1)(j-1)>& a_ <(i-1)(j+1)>& \cdots & a_ <(i-1)n>\\ a_ <(i+1)1>& a_ <(i+1)2>& \cdots & a_ <(i+1)(j-1)>& a_ <(i+1)(j+1)>& \cdots & a_ <(i+1)n>\\ \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ & a_ & \cdots & a_ \\ \end[/math]

Источник

Метод присоединенной матрицы

Определение обратной матрицы

ОБРАТНЫЕ МАТРИЦЫ

ЛЕКЦИЯ 3

Обратная матрица Метод присоединенной матрицы. Матричные уравнения. Матричный способ решения систем линейных уравнений. Ранг матрицы. Метод окаймляющих миноров. Метод элементарных преобразований. Теорема о базисном миноре.

Матрица А –1 называется обратной матрицей по отношению к матрице А, если выполняется равенство

Из данного определения следует, что взаимообратные матрицы перестановочны. Это означает, что только квадратные матрицы могут иметь обратные. Однако не каждая квадратная матрица имеет обратную. Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля: detA¹0.

% Действительно, из определения обратной матрицы и свойств определителей получаем: det(A –1 A)=detA –1 detA=detE=1, откуда следует необходимое условие существования обратной матрицы: detA¹0 или detA –1 ¹0. Вопрос о доказательстве достаточности этого условия несколько сложнее. Для этого нужно указать алгоритм построения такой матрицы. Поэтому мы вернемся к этому вопросу позднее (см. метод присоединенной матрицы).

Отметим, что если обратная матрица существует, то такая матрица только одна. Действительно, пусть существует еще одна матрица В, удовлетворяющая условию АВ=ВА=Е, тогда можно написать:

Матрица, определитель которой отличен от нуля, называется невырожденной, или неособенной; в противном случае она называется вырожденной, или особенной. Необходимое и достаточное условие существования обратной матрицы можно сформулировать следующим образом: обратная матрица существует, причем только одна, тогда и только тогда, когда исходная матрица невырожденная.

Для невырожденных матриц справедливы следующие свойства:

Матрица A Ú называется присоединенной к матрице A, если она является транспонированной к матрице A, а вместо элементоввзяты их алгебраические дополнения, т.е.

Теорема 3.1. Обратная и присоединенная матрицы связаны соотношением

(3.2)

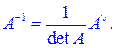
% Действительно, рассмотрим произведение матриц

При этом учтем, что сумма произведений элементов некоторой строки или столбца на их алгебраические дополнения равно определителю матрицы (см. теорему о разложении определителя по строке или столбцу).Дополнительно мы воспользуемся еще одним свойством определителей: сумма произведений алгебраических дополнений некоторой строки или столбца на соответствующие элементы другой строки или столбца равно нулю. Это связано с тем, что такая сумма эквивалентна определителю, у которого две одинаковые строки или столбца, и, следовательно, он будет равен нулю. Таким образом, перемножая рассматриваемые матрицы, получим

Отсюда следует справедливость приведенной теоремы. Более того, фактически мы указали алгоритм построения обратной матрицы при помощи присоединенной матрицы и тем самым доказали достаточное условие существования обратной матрицы. &

Общая схема нахождения обратной матрицы
(метод присоединенной матрицы):

1) Вычисляем определитель заданной матрицы, если он равен нулю, то обратной матрицы не существует.

2) Транспонируем заданную матрицу.

3) Вычисляем все алгебраические дополнения транспонированной матрицы.

4) Составляем присоединенную матрицу, т.е. вместо элементов транспонированной матрицы ставим их алгебраические дополнения.

5) Записываем обратную матрицу. Для этого каждый элемент присоединенной матрицы делим на определитель исходной матрицы.

Решение. 1) detA = –4.

2)

3) Ищем алгебраические дополнения транспонированной матрицы (не забывать учитывать знаки алгебраических дополнений!):

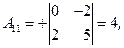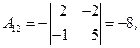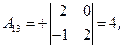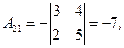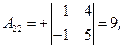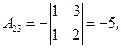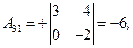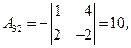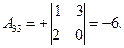4) Составляем присоединенную матрицу:

5) Записываем обратную матрицу:

6) Делаем проверку: AA –1 = A –1 A = E:

Следовательно, обратная матрица найдена правильно. à

Пример 3.2. Найти обратную матрицу

Решение. Поскольку

Эту формулу можно использовать для нахождения обратных матриц второго порядка. à

Источник

Присоединенная матрица и алгоритм ее составления

Дата добавления: 2015-07-23 ; просмотров: 9564 ; Нарушение авторских прав

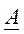
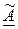
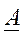
Для любой квадратной матрицы можно составить другую квадратную матрицу такого же порядка, называемую присоединенной к матрице , если каждый элемент a_ij исходной матрицы заменить его алгебраическим дополнением A_ij , а затем полученную матрицу этих алгебраических дополнений транспонировать.

Ex. Пусть дана исходная матрица порядка (3 ´ 3)

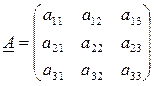Чтобы составить присоединенную к ней матрицу 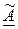, необходимо:

1. Найти для каждого элемента a_ij исходной матрицы их алгебраические дополнения A_ij и составить из них матрицу алгебраических дополнений

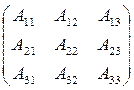2. Транспонировать полученную матрицу алгебраических дополнений

12. Обратная матрица: условия ее существования
и алгоритм составления

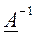
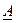
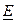
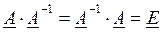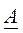
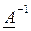
Def. Матрица называется обратной по отношению к квадратной матрице , если при перемножении этих матриц получается единичная матрица той же размерности, т.е.

Def. Матрица называется обратимой, если для нее существует обратная матрица .

Теорема. Матрица 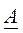будет обратимой тогда и только тогда, когда она является квадратной и невырожденной матрицей

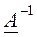
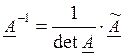Обратная матрица определяется из соотношения

т.е. алгоритм ее составления включает следующие шаги:

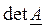
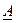
1. вычисляем определитель исходной матрицы , если он не равен нулю, то матрица является обратимой и можно переходить к следующему шагу;

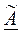
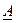
2. используя п.10 данной темы составляем матрицу , присоединенную к исходной матрице ;

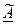
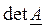
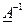
3. делим каждый элемент присоединенной матрицы на число , в результате получим искомую обратную матрицу .

Свойства обратной матрицы

1. Для взаимно обратных матриц выполняется переместительный закон умножения

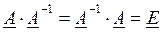
2. При обращении обратной матрицы получается исходная матрица

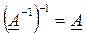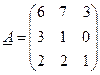Ex. Составить матрицу, обратную для

1.Составим и вычислим определитель исходной матрицы

2.Вычислим алгебраические дополнения A_ij для каждого элемента a_ij исходной матрицы и составим промежуточную матрицу алгебраических дополнений

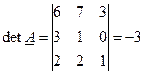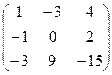
3.Транспонируя матрицу алгебраических дополнений, получим матрицу

, присоединенную к исходной матрице

4.Делим каждый элемент присоединенной матрицы на

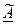
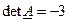
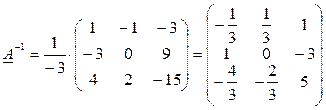Чтобы убедится в правильности выполненных расчетов, перемножим исходную и обратную ей матрицы, при этом получится единичная матрица

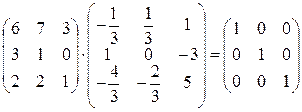Обратные матрицы широко используются при решении систем линейных уравнений в матричной форме, при статистическом анализе массивов информации и решении других практических задач. Естественно, что составление обратных матриц связано с большими объемами арифметических вычислений и реализуется на ЭВМ при помощи специальных программ и процедур.

Не нашли то, что искали? Google вам в помощь!

Источник

Теорема. Опр. Матрица называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы

Обратная матрица

= (3.1)

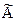
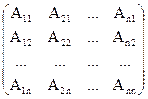
Опр. Квадратная матрица А называется вырожденной (особенной), если ее определитель |A|=0, и невырожденной, если ее определитель |A|¹0.

Пусть матрица А – невырожденная, то есть |A|¹0. Тогда, по правилу умножения матриц, по теореме Лапласа и по свойству 9 определителей, получим

А× = × = =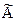

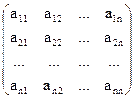
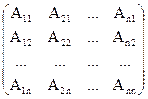
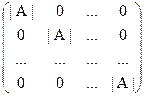
= |A|× 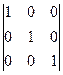= |A|×E

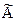
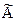
Следовательно, А× = |A|×E. Аналогично доказывается, что ×А = |A|×E.

Свойства обратной матрицы:

Источник