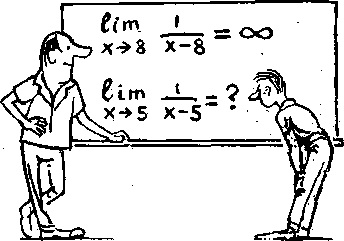Что такое пределы в математике

Что такое предел функции

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

Знаменатель () изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на ():

5. Остается только подставить число 1 в выражение, получившееся под пределом:

Источник

Как решать пределы для чайников?

Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.

Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.

Примеры решений

Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Внимание «чайникам» 🙂 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать:

Продолжаем решать учитывая вышеприведенное преобразование:

Используя определение из примера 2 и подставляя в место х бесконечность получаем:

Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем.

Алгоритм вычисления лимитов

В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.

Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!

Источник

Предел функции: основные понятия и определения

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

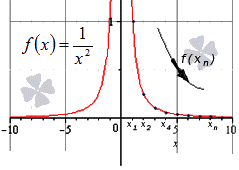
В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

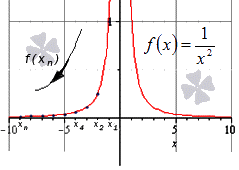
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

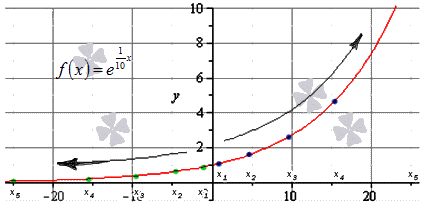
Решение

Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник

Предел (математика)

Предел — это математический термин, обозначающий некое предельное число, к которому стремится бесконечная последовательность или функция. Соответственно, различают предел последовательности и предел функции (в точке, «на бесконечности»). Считается также, что предел может быть равен «бесконечности».

Интуитивно понятно, что бывает стремление одного предмета к другому, например птица стремится к гнезду. Отсюда проистекает интуитивное понятие стремления последовательности или функции к чему-то, в рамках математического анализа это понятие стремления находит свою формализацию в математических определениях предела функции и предела последовательности.

Содержание

[править] Предел последовательности

Пределом числовой последовательности n> называется число A, в ε-окрестность которого попадают все члены последовательности с номером больше номера N(ε).

[math]\lim\limits_x_n = A \Leftrightarrow \forall \varepsilon \gt 0 \ \exists N(\varepsilon) \in \mathbb \text < такое, что >\forall n \gt N(\varepsilon) \Rightarrow \left|x_n-A\right| \lt \varepsilon[/math]

[править] Виды пределов

[править] Свойства пределов

[править] Предел функции

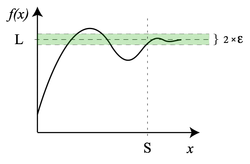
Пределом функции f в точке a называется число A, в ε-окрестность которого попадают все значения функции в точках из δ-окрестности точки a.

[math]\lim\limits_f(x)= A \Leftrightarrow \forall \varepsilon \gt 0 \ \exists \delta(\varepsilon) \gt 0 \text < такое, что >\forall x \in \mathbb, \ \left|x-a\right| \lt \delta \Rightarrow \left|f(x)-A\right| \lt \varepsilon[/math]

[править] Виды пределов

[править] Свойства пределов

Для функций u=f(x) и v=g(x) верны правила:

Источник

Предел (математика)

Понятие предела на интуитивном уровне использовалось ещё во второй половине XVII века Ньютоном, а также математиками XVIII века, такими как Эйлер и Лагранж. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.

Предел последовательности

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.

Предел функции

Функция имеет предел в точке , если для всех значений , достаточно близких к , значение близко к .

См. также

Полезное

Смотреть что такое «Предел (математика)» в других словарях:

Предел — объект, представляющий собой воображаемую или реальную границу для другого объекта. В математическом анализе см. Предел (математика), а также: Предел последовательности Предел функции Предел категории Частичный предел Проективный предел Банаховы… … Википедия

Предел вдоль фильтра — обобщение понятия предела. Содержание 1 Определение фильтра 2 Определение предела … Википедия

Предел Человеческого Разума — Предел Человеческого Разума ♦ Bornes de L’esprit Humain Традиционное выражение, стремящееся подчеркнуть, что мы не Бог и не способны к абсолютному познанию абсолюта. Оспаривать этого я, разумеется, не стану. Но насколько подходит сюда слово… … Философский словарь Спонвиля

МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера

МАТЕМАТИКА — уч. предмет в школе, в содержание к рого входят элементы арифметики, алгебры, начал анализа, евклидовой геометрии плоскости и пространства, аналитич. геометрии, тригонометрии. Преподавание М. направлено на овладение учащимися системой матем.… … Российская педагогическая энциклопедия

Предел — одно из основных понятий математики. П. постоянная, к которой неограниченно приближается некоторая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие П. числовой … Большая советская энциклопедия

Математика инков — Кипукамайок из книги Гуамана Пома де Айяла «Первая Новая Хроника и Доброе Правление». Слева у ног кипукамайока юпана, содержащая вычисления священного числа для песни «Сумак Ньюста» (в оригинале рукописи рисунок не цветной, а чёрно белый;… … Википедия

Предел (теория категорий) — У этого термина существуют и другие значения, см. Предел. В теории категорий предел диаграммы это конструкция, обобщающая многие универсальные диаграммы самой теории категорий. Примеры Уравнитель Произведение Коуниверсальный квадрат… … Википедия

Источник