Что такое предельная точка

ПРЕДЕЛЬНАЯ ТОЧКА

Лит.:[1] Александров II. С., Введение в теорию множеств и общую топологию, М., 1977; [2] Xаусдорф Ф., Теория множеств, пер. с нем., М.- Л., 1937.

Смотреть что такое «ПРЕДЕЛЬНАЯ ТОЧКА» в других словарях:

предельная точка — точка накопления Словарь русских синонимов … Словарь синонимов

Предельная точка — множества в общей топологии это такая точка, любая проколотая окрестность которой пересекается с этим множеством. Содержание 1 Определение 2 Связанные понятия и свойства … Википедия

предельная точка — ribinis taškas statusas T sritis fizika atitikmenys: angl. limit point; limiting point vok. Grenzpunkt, m rus. граничная точка, f; предельная точка, f pranc. point limite, m … Fizikos terminų žodynas

Предельная точка — множества А, такая точка ξ пространства, сколь угодно близко от которой имеются отличные от ξ точки множества А, т. е. в любой окрестности (См. Окрестность) которой содержится бесконечное множество точек из А. Характеристическим свойством … Большая советская энциклопедия

предельная точка — Syn: точка накопления … Тезаурус русской деловой лексики

предельная точка профиля зуба — предельная точка профиля Точка пересечения теоретического профиля зуба с предельной линией его теоретической поверхности. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины понятия, относящиеся к зубчатому колесупрофиль зуба Синонимы… … Справочник технического переводчика

предельная точка действующей линии теоретической поверхности зуба — предельная точка действующей линии Каждая из точек, ограничивающих действующую линию теоретической поверхности зуба. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины объемные элементы и поверхности зубапонятия, относящиеся к… … Справочник технического переводчика

предельная точка линии зацепления — Каждая из точек, ограничивающих линию зацепления зубчатой передачи и соответствующих предельным точкам действующей линии теоретической поверхности зуба, которая при линейном контакте является точкой пересечения линии зацепления с предельной… … Справочник технического переводчика

Точка (матем.) — Точка (математическая), одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых состоят… … Большая советская энциклопедия

Источник

Предельная точка

Смотреть что такое «Предельная точка» в других словарях:

предельная точка — точка накопления Словарь русских синонимов … Словарь синонимов

Предельная точка — множества в общей топологии это такая точка, любая проколотая окрестность которой пересекается с этим множеством. Содержание 1 Определение 2 Связанные понятия и свойства … Википедия

предельная точка — ribinis taškas statusas T sritis fizika atitikmenys: angl. limit point; limiting point vok. Grenzpunkt, m rus. граничная точка, f; предельная точка, f pranc. point limite, m … Fizikos terminų žodynas

ПРЕДЕЛЬНАЯ ТОЧКА — множества точка, в любой окрестности к рой содержится по крайней мере одна точка данного множества, отличная от нее самой. Рассматриваемые множества и точка предполагаются принадлежащими нек рому топологич. пространству. Множество, содержащее все … Математическая энциклопедия

предельная точка — Syn: точка накопления … Тезаурус русской деловой лексики

предельная точка профиля зуба — предельная точка профиля Точка пересечения теоретического профиля зуба с предельной линией его теоретической поверхности. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины понятия, относящиеся к зубчатому колесупрофиль зуба Синонимы… … Справочник технического переводчика

предельная точка действующей линии теоретической поверхности зуба — предельная точка действующей линии Каждая из точек, ограничивающих действующую линию теоретической поверхности зуба. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины объемные элементы и поверхности зубапонятия, относящиеся к… … Справочник технического переводчика

предельная точка линии зацепления — Каждая из точек, ограничивающих линию зацепления зубчатой передачи и соответствующих предельным точкам действующей линии теоретической поверхности зуба, которая при линейном контакте является точкой пересечения линии зацепления с предельной… … Справочник технического переводчика

Точка (матем.) — Точка (математическая), одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых состоят… … Большая советская энциклопедия

Источник

Математика, физика на «отлично»

Предельная точка

Понятие предельной точки уже очень близко к понятию предел последовательности, но пока что операции мы всё равно проводим над множествами. Для того, чтобы более наглядно представлять себе нижеизложенные теоремы, старайтесь ситуацию изобразить на рисунке.

В теории множеств выделяют предельные и изолированные точки множества. Перед тем, как дать точные определения и доказательства, приведём пример на числовой оси. Пусть М = (3;10) ∪ <20>. В данном случае точки m = [3;10] являются предельными, а точка m = 20 — изолированной.

Существует 2 эквивалентных определения предельной точки:

Определение:
х ∈ М ⊂ Е является предельной точкой М, если:
1) ∀ε > 0 в U_ε(x) содержится бесконечное число точек из М
2) ∀ε > 0 в Uº_ε(x) содержится хотя бы одна точка из М

Теорема 2. Из 2) следует 1)
Доказательство: Предположим, что если утверждение 2) верно, то утверждение 1) — неверно, то есть в окрестности х по ε содержится конечное число точек. Пусть x_i∈ М, x_i ≠ х. Тогда учитывая конечность выбранного множества мы можем определить ω = min|x — x_i|
Рассмотрим проколотую окрестность х по ε = ω. Но тогда:
U_ω(х) ∩ М = х, откуда следует, что
Uº_ω(х) ∩ М = ∅, что противоречит условию 2). Наше предположение неверно, утверждение 1) является верным, ч.т.д.

Докажем ещё одну теорему связанную с предельной точкой.
Теорема 3. Если точка принадлежит граничному множеству и не является изолированной, то она является предельной.
Доказательство: Предположим, что произвольно выбранная граничная точка не является предельной. Тогда существует такое ε > 0 что Uº_ε(x) ∩ М= ∅ (не является предельной) и для любого ε > 0 выполняется, что Uº_ε(x) ∩ М ≠ ∅ (определение граничной точки).
∃ε > 0 : Uº_ε(x) ∩ М= ∅
∀ε > 0 ⇒ Uº_ε(x) ∩ М ≠ ∅
Однако эти 2 полученных вывода противоречат друг другу, а значит наше предположение неверно, граничная точка является предельной, ч.т.д.

Удачи и положительных оценок на контрольных, зачётах и экзаменах!

Источник

ПРЕДЕЛЬНАЯ ТОЧКА

(1) (a-предельная точка) или

(2)

(w-предельная точка), где <t k >, kN,- последовательность такая, что при в (1) или при в (2) и пределы (1) или (2) существуют.

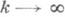
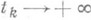
Лит.:[1] Немыцкий В. В., Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М., 1949. В. М. Миллионщиков.

Смотреть что такое «ПРЕДЕЛЬНАЯ ТОЧКА» в других словарях:

предельная точка — точка накопления Словарь русских синонимов … Словарь синонимов

Предельная точка — множества в общей топологии это такая точка, любая проколотая окрестность которой пересекается с этим множеством. Содержание 1 Определение 2 Связанные понятия и свойства … Википедия

предельная точка — ribinis taškas statusas T sritis fizika atitikmenys: angl. limit point; limiting point vok. Grenzpunkt, m rus. граничная точка, f; предельная точка, f pranc. point limite, m … Fizikos terminų žodynas

ПРЕДЕЛЬНАЯ ТОЧКА — множества точка, в любой окрестности к рой содержится по крайней мере одна точка данного множества, отличная от нее самой. Рассматриваемые множества и точка предполагаются принадлежащими нек рому топологич. пространству. Множество, содержащее все … Математическая энциклопедия

Предельная точка — множества А, такая точка ξ пространства, сколь угодно близко от которой имеются отличные от ξ точки множества А, т. е. в любой окрестности (См. Окрестность) которой содержится бесконечное множество точек из А. Характеристическим свойством … Большая советская энциклопедия

предельная точка — Syn: точка накопления … Тезаурус русской деловой лексики

предельная точка профиля зуба — предельная точка профиля Точка пересечения теоретического профиля зуба с предельной линией его теоретической поверхности. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины понятия, относящиеся к зубчатому колесупрофиль зуба Синонимы… … Справочник технического переводчика

предельная точка действующей линии теоретической поверхности зуба — предельная точка действующей линии Каждая из точек, ограничивающих действующую линию теоретической поверхности зуба. [ГОСТ 16530 83] Тематики передачи зубчатые Обобщающие термины объемные элементы и поверхности зубапонятия, относящиеся к… … Справочник технического переводчика

предельная точка линии зацепления — Каждая из точек, ограничивающих линию зацепления зубчатой передачи и соответствующих предельным точкам действующей линии теоретической поверхности зуба, которая при линейном контакте является точкой пересечения линии зацепления с предельной… … Справочник технического переводчика

Точка (матем.) — Точка (математическая), одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых состоят… … Большая советская энциклопедия

Источник

Предельные точки последовательности. Числовая прямая

По этой ссылке вы найдёте полный курс лекций по математике:

Поэтому достаточно очевидно следующее утверждение. Утверждение б.б. Если lim = 6 6 R, то b — единственная предельная точка последовательности <хп>. Действительно, в силу определения 6.3 предела последовательности все ее элементы начиная с некоторого номера попадают в любую сколь угодно малую окрестность точки 6, а потому в окрестность никакой другой точки не могут попасть элементы с произвольно большими номерами.

Следовательно, условие определения 6.7 выполнимо лишь для единственной точки 6. Однако не всякая предельная точка (иногда ее называют тонкой сгущенил) последовательности является ее пределом. Так, последовательность (б.б) не имеет предела (см. пример 6.5), но имеет две предельные точки х = 1 и х = — 1. Последовательность <(-1)пп>в качестве предельных имеет две бесконечные точки +оо и —со расширенной числовой прямой, объединение которых обозначают одним символом оо.

Очевидно, что если имеет пределом число 6, то любая ее подпоследовательность имеет тот же самый предел, поскольку начиная с некоторого номера все элементы как исходной последовательности, так и любой ее подпоследовательности попадают в любую выбранную окрестность точки 6. В то же время любая предельная точка подпоследовательности является предельной и для последовательности. Теорема в.9. Из любой последовательности, имеющей предельную точку, можно выбрать подпоследовательность, имеющую своим пределом эту предельную’точку. Пусть b — предельная точка последовательности <хп>.

Теорема 8.10. Если некоторая последовательность имеет подпоследовательность с пределом 6, то Ь есть предельная точка этой последовательности. Из определения 6.3 предела последовательности следует, что начиная с некоторого номера все элементы подпоследовательности с пределом b попадают в окрестность U(b, е) произвольного радиуса е. Поскольку элементы подпоследовательности являются одновременно элементами последовательности <хп>> внутрь этой окрестности попадают элементы хп со сколь угодно большими номерами, а это в силу определения 6.7 означает, что Ь — предельная точка последовательности <яп>.

Возможно вам будут полезны данные страницы:

Замечание 0.2. Теоремы 6.9 и 6.10 справедливы и в случае, когда предельная точка является бесконечной, если при доказательстве вмерто окрестности U(6, 1 /п) рассматривать окрестность (или окрестности Условие, при котором из последовательности можно выделить сходящуюся подпоследовательность, устанавливает следующая теорема. Теорема 6.11 (Больцано — Веиерштрасса). Всякая ограниченная последовательность содержит подпоследовательность, сходящуюся к конечному пределу.

Пусть все элементы последовательности <ап>заключены между числами а и 6, т.е. хп € [а, b] Vn € N. Разделим отрезок [а, Ь] пополам. Тогда хотя бы одна из его половин будет содержать бесконечное множество элементов последовательности, так как в противном случае и весь отрезок [а, Ь] содержал бы конечное их число, что невозможно. Пусть ] будет та из половин отрезка [а, 6], которая содержит бесконечное множество элементов последовательности <жп>(или если обе половины таковы, то любая из них). Аналогично из отрезка [ai, b<\ выделим его половину [a2) 62], содержащую бесконечное множество элементов последовательности, и т.д.

Согласно определению 6.7 х — предельная точка этой последовательности. Тогда в силу теоремы 6.9 существует подпоследовательность, сходящаяся к точке х. Метод рассуждений, использованный при доказательстве этой теоремы (ее иногда называют леммой Больцано — Вейер-штрасса) и связанный с последовательным делением пополам рассматриваемых отрезков, известен под названием метода Больцано. Эта теорема значительно упрощает доказательство многих сложных теорем.

Она позволяет доказать иным (иногда более простым) путем ряд ключевых теорем.

Дополнение 6.2. Доказательство признака Вейерштрасса и критерия Коши Сначала докажем утверждение 6.1 (признак Вейерштрасса сходимости ограниченной монотонной последовательности). Предположим, что последовательность <яп>неубывающая. Тогда множество ее значений ограничено сверху и по теореме 2.1 имеет точную верхнюю граньу которую обозначим sup be R. В силу свойств точной верхней грани (см. 2.7) Предельные точки последовательности числовая прямая Доказательство признака Вейерштрасса и критерия Коши.

Согласно определению 6.1 для неубывающей последовательности имеем или Тогда > Ny а с учетом (6.34) получим что соответствует определению 6.3 предела последовательности, т.е. 31im и lim = 66R. Если последовательность <хп>невозрастающая, то ход доказательства аналогичен. Теперь перейдем к доказательству достаточности критерия Кохии сходимости последовательности (см. утверждение 6.3), поскольку необходимость условия критерия следует из теоремы 6.7.

Обозначим ее через Ь. Таким образом, при Из сравнения (6.36) и (6.37) в итоге получим что соответствует определению 6.3 предела последовательности, т.е. 31im и lim = 6 6 R. Фундаментальные последовательности начал изучать Боль-цано. Но он не располагал строгой теорией действительных чисел, и поэтому ему не удалось доказать сходимость фундаментальной последовательности. Это сделал Коши, приняв за очевидное принцип вложенных отрезков, который позднее обосновал Кантор.

Имя Коши получил не только критерий сходимости последовательности, но и фундаментальную последовательность часто именуют последовательностью Коши, а имя Кантора носит принцип вложенных отрезков. Вопросы и задачи 8.1. Доказать, что: 6.2. Привести примеры несходящихся последовательностей с элементами, принадлежащими множествам Q и R\Q. 0.3. При каких условиях члены арифметической и геометрической прогрессий образуют убывающую и возрастающую последовательности? 6.4. Доказать соотношения, которые следуют из табл. 6.1. 6.5.

Являются ли монотонными последовательности <-хп>, <1>и <х£>, если последовательность <хп>возрастающая? Могут ли быть первые три последовательности монотонными, если последовательность <хп>немонотонная? в.14. Доказать, что если сходящаяся последовательность <хп>возрастает, то lim = sup. 6.15. Пусть <хп>и <уп>— возрастающие последовательности и Vn 6 N х„ ^ уп. Доказать, что: Предельные точки последовательности числовая прямая.

и критерия Коши. 1) если <уп>сходится, то и <хп>сходится; 2) если <хп>расходится, то и <уп>расходится. 6.16. Доказать, что существует единственная точка г, принадлежащая любому из отрезков, левым концом которого является элемент возрастающей последовательности <яп>, а правым — элемент с тем же номером убывающей последовательности <уп>> причем уп-£п-»0 при п-»оо. в.17.

Последовательности <хп>и <уп>определены заданием элементов х\ и у\ при условии 0 и рекуррентными формулами хп+1 = (хп + уп)/2 и Уп+1 = 2хпуп/(х п «Ь Уп)* Доказать, что эти последовательности строго монотонные и сходятся к одному и тому же пределу. Найти этот предел. в.18. Доказать сходимость и вычислить предел последовательностей: 6.19. Привести примеры последовательностей, не являющихся фундаментальными. 6.20.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник