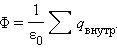Что такое поток вектора напряженности

Что такое поток вектора напряженности

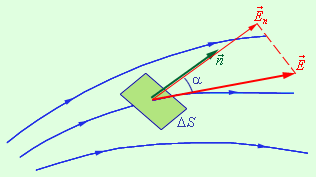
Итак, на примерах мы показали, что, если силовые линии однородного электрического поля напряженностью пронизывают некоторую площадку S, то поток вектора напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой:

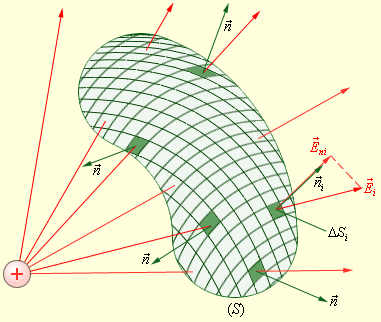
Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф_Е через эту поверхность.

В векторной форме можно записать – скалярное произведение двух векторов, где вектор .

Таким образом, поток вектора есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.

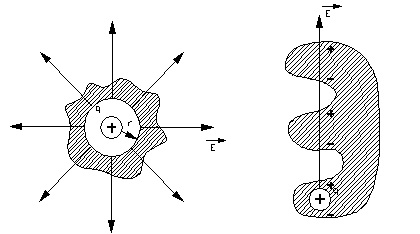
Рассмотрим примеры, изображенные на рисунках 2.6 и 2.7.

Для рисунка 2.6 – поверхность А₁ окружает положительный заряд и поток здесь направлен наружу, т.е. Поверхность А₂ – окружает отрицательный заряд, здесь и направлен внутрь. Общий поток через поверхность А равен нулю.

Для рисунка 2.7 – поток будет не равен нулю, если суммарный заряд внутри поверхности не равен нулю. Для этой конфигурации поток через поверхность А отрицательный (подсчитайте число силовых линий).

Таким образом, поток вектора напряженности зависит от заряда. В этом смысл теоремы Остроградского-Гаусса.

Источник

Теорема Гаусса

Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.

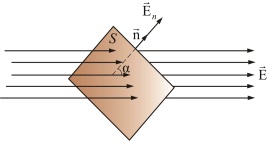
Поток вектора напряженности

Δ Φ = E Δ S cos α = E n Δ S.

Φ = ∑ ∆ Φ i = ∑ E m ∆ S i

Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.

Теорема Гаусса. Доказательство

Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.

Уравнение Гаусса имеет вид:

Φ = 1 ε 0 ∑ q в н у т р

где R является радиусом сферы.

Так, мы доказали теорему Гаусса.

Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.

Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).

Применение теоремы Гаусса

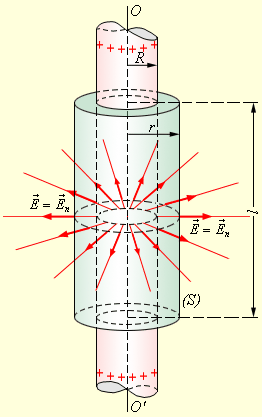
Если r ≥ R , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2 π r l . Применим закон Гаусса и получим:

В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:

Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.

Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.

К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).

При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.

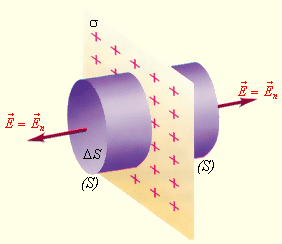
Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:

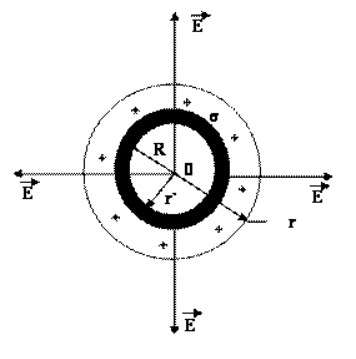
Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.

Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.

Источник

Поток вектора напряженности электростатического поля

Понятие потока вектора напряженности электростатического поля

Полноценно описать электростатическое поле заданной системы зарядов в вакуумной среде можно с помощью эксперимента, подтверждением которого служит закон Кулона, и принципа суперпозиции. При этом есть возможность представить свойства электростатического поля в обобщенном виде без применения утверждения о кулоновском поле точечного заряда. В этом случае целесообразно обратиться к теореме, которая была выведена немецким ученым К. Гауссом, определяющей поток вектора напряженности сквозь произвольную замкнутую поверхность.

Поток вектора представляет собой поверхностный интеграл от нормальной составляющей этого вектора.

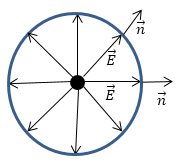
Представим, что через некую площадь S проходят силовые линии однородного электрического поля, напряженность которого равна:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Тогда поток напряженности или количество силовых линий, проходящих через площадку, будет рассчитываться по формуле:

Где En является произведением вектора \(\vec\) и нормали \(\vec\) к данной площадке.

Поток вектора напряженности \(\Phi _\) через заданную поверхность представляет собой полное число силовых линий, которые проходят через эту поверхность площадью S.

Формула расчета

Утверждение можно записать в векторной форме. Тогда уравнение будет являться скалярным произведением двух векторов:

Где вектор \(\vec\) равен:

Таким образом, поток вектора \(\vec\) является скалярной величиной, которая в зависимости от угла α может обладать положительным или отрицательным значением. Утверждения можно представить схематично.

На первом изображении поверхность А1 расположена вокруг положительного заряда, поток направлен наружу, то есть:

Поверхность А2 окружает отрицательный заряд, поток направлен внутрь, то есть:

Общий поток А обладает нулевым значением.

На втором рисунке при условии отличия суммарного заряда внутри поверхности от нуля, поток также не равен нулю. В данной системе поток через поверхность А характеризуется отрицательной величиной. Таким образом, поток вектора напряженности связан с зарядом. В этом заключается смысл теоремы Островского-Гаусса.

Доказательство теоремы Гаусса

Согласно данной закономерности, поток вектора напряженности электростатического поля сквозь произвольную поверхность определяют поток вектора. В единицах измерения СИ \(\Phi _\) = 1 В´м. Вначале необходимо выполнить расчет потока вектора напряженности сквозь сферическую поверхность радиуса r, которая охватывает точечный заряд q, размещенный в ее центральной точке. Формула будет иметь следующий вид:

Уравнение применимо в случае замкнутой поверхности разной формы. Если выделить сферу с помощью произвольной замкнутой поверхности, то каждая линия напряженности, которая пронизывает сферу, будет проходить через эту поверхность.

Можно представить, что заряд q охватывает какая-то замкнутая поверхность. В случае, когда линии напряженности будут выходить из поверхности, поток станет положительным. Если линии напряженности входят в поверхность, то поток напряженности будет обладать отрицательным значением. Нечетное количество пересечений в процессе расчета потока приводят к одному пересечению.

В виде формулы утверждение можно записать в следующем виде:

Данную теорему вывел математически для векторного поля любой природы русский математик М.В. Остроградский, а затем независимо от него для электростатического поля — К. Гаусс. В случае, когда заряд не проходит через замкнутую поверхность, то поток будет иметь нулевое значение. Можно представить произвольную поверхность, окруженную N зарядами, тогда

Поток вектора напряженности:

Представленное уравнение демонстрирует поток вектора напряженности через произвольную замкнутую поверхность, которая включает совокупность N зарядов, для электростатического поля в вакуумной среде. Для общего случая характерно распределение электрических зарядов с объемной плотностью r, которая неодинакова в разных точках пространства. В таком случае теорема Гаусса будет иметь следующий вид:

Когда поле Е определяется конфигурацией всех зарядов, поток вектора Е через произвольную замкнутую поверхность S зависит от алгебраической суммы зарядов, которые расположены внутри поверхности S. При передвижении зарядов без пересечения поверхности S поток вектора Е сквозь эту поверхность останется прежним.

Применение теоремы Гаусса

Решения формул можно получить с помощью интегрирования уравнения:

Где V является объемом, для которого r не равен нулю.

Но, благодаря использованию теоремы Гаусса, решение задач упрощается. Однако данный метод не всегда можно применить. Он эффективен лишь для ситуаций, когда поле характеризуется специальной симметрией:

Условия применения теоремы Гаусса:

В случае, когда данные условия не выполнимы, расчет Е поля производят другими методами, к примеру, ДИ-дифференцирование и интегрирование. При дискретном распределении зарядов формула будет иметь следующий вид:

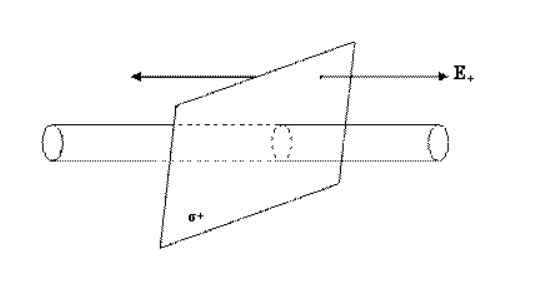
Применение теоремы Гаусса для расчета напряженности поля равномерно заряженной бесконечной плоскости

Можно представить бесконечную плоскость. Она заряжена с поверхностной плотностью зарядов:

Линии напряженности расположены перпендикулярно относительно плоскости и направлены в обе стороны от плоскости. Поверхность цилиндра можно представить в роли замкнутой поверхности. Основания этой фигуры находятся параллельно по отношению к бесконечной плоскости, а ее ось — перпендикулярна плоскости.

Образующие цилиндрической фигуры расположены параллельно, относительно линий напряженности:

Поток вектора напряженности через боковую поверхность равен нулю, а полный поток через цилиндр определяется совокупностью потоков, которые проходят через его основания. Для основания:

Заряд, который заключен внутри постоянной замкнутой поверхности, определяется, как:

Численная характеристика потока равна:

Согласно теореме Гаусса:

Исходя из данного уравнения, следует:

Напряжение электростатического поля, которое образовано с помощью равномерно заряженной бесконечной плоскости, составляет:

В этом случае напряжение электростатического поля не определяется длиной цилиндра. При любом расстоянии от плоскости напряжение будет одинаково по модулю. Поле равномерно заряженной плоскости отличается однородностью.

Применение теоремы Гаусса для расчета напряженности поля двух разноименно заряженных плоскостей, которые бесконечно параллельны друг относительно друга

Схематичное представление таких плоскостей представлено на рисунке. Можно представить, что левая плоскость заряжена e + s, а правая с – s.

Суммарное поле можно рассчитать с помощью определения суперпозиции полей, каждую из которых создают плоскости:

Таким образом, определяется результирующая напряженность поля в области, отделяющей две плоскости. За пределами рассматриваемого объема, который ограничен этими плоскостями, результирующая напряженность поля будет равна нулю.

Применение теоремы Гаусса для расчета напряженности поля равномерно заряженной сферической поверхности

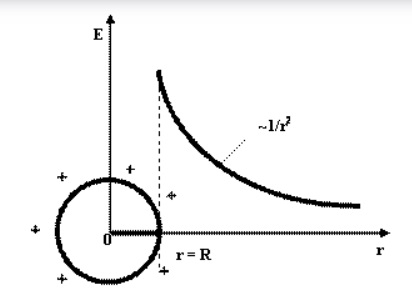
Можно представить сферу, которая равномерно заряжена и обладает радиусом R. Поверхностная плотность заряда равна +s. Для данного поля характерна сферическая симметрия и радиальное направление линий напряженности. Мысленно можно выделить сферу, радиус которой равен r, а центр совпадает с центральной точкой заряженной сферы. Предположим, что r>R. В этом случае справедлива формула:

Рисунок демонстрирует график зависимости E = f (r)

Пример расчета напряженности поля объемно заряженного шара

Допустим, что шарообразный объект обладает радиусом R. Шар равномерно заряжен, а объемная плотность заряда составляет:

Для данного поля характерна сферическая симметрия. Можно представить сферу замкнутой поверхностью. Когда r>R,

В случае, когда r \(q_=q\left( \frac>\right)^<3>\)

Данное уравнение справедливо, так как заряды относятся, как объемы, а объемы, как кубы радиусов. В таком случае, исходя из теоремы Гаусса, следует уравнение:

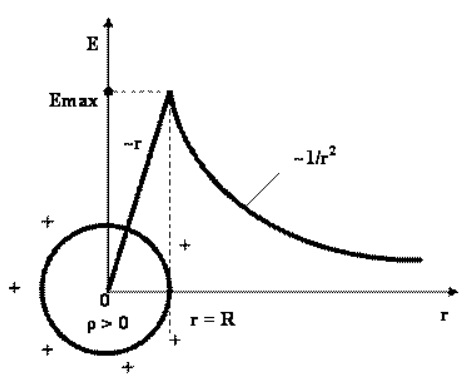
График демонстрирует зависимость E = f (r)

Внутри шара, который заряжен равномерно, напряженность увеличивается линейно с расстоянием r от его центра. Вне шара напряженность будет уменьшаться обратно пропорционально r2.

Пример расчета напряженности поля бесконечного круглого цилиндра, который заряжен и обладает линейной плотностью заряда I

Имеется объект цилиндрической формы с радиусом R. Линии напряженности обладают одинаковой густотой и направлены вдоль радиусов круговых сечений цилиндра. Замкнутая поверхность будет представлена в виде цилиндра, радиус которого равен r, а высота — h. Поток вектора через торцы фигуры обладает нулевым значением, а через боковые поверхности составляет:

Следует учитывать, что:

В случае, когда l > 0, получаем E > 0, то есть вектор Е будет ориентирован от цилиндра. Если l

Источник

Что такое поток вектора напряженности

Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.

Теорема Гаусса утверждает:

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀.

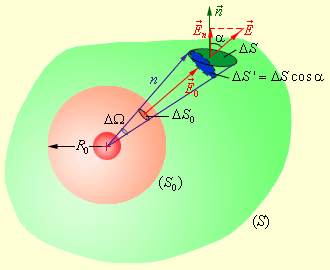
Окружим теперь точечный заряд произвольной замкнутой поверхностью и рассмотрим вспомогательную сферу радиуса (рис. 1.3.3).

Таким образом, теорема Гаусса доказана.

Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.

Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.

Этот результат не зависит от радиуса заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.

Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.

Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).

Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.

Источник

Поток вектора напряженности электрического поля

Вы будете перенаправлены на Автор24

Элементарный поток вектора напряженности

\[dФ_E=EdScos\alpha =\overrightarrow\cdot d\overrightarrow\ \left(2\right),\]

\[Ф_E=\int\limits_S<\overrightarrow\cdot d\overrightarrow>\ \ \left(4\right).\]

Направление нормали

Принято считать, что если имеют дело с замкнутой поверхностью, то нормаль имеет положительное направление наружу. Поток вектора напряженности в случае замкнутой поверхности записывают через криволинейный интеграл по замкнутой поверхности:

\[Ф_E=\oint\limits_S<\overrightarrow\cdot d\overrightarrow>\ \ \left(5\right).\]

Задание: Напряженность электростатического поля задана формулой в декартовых координатах:

В качестве основы для решения используем определение потока вектора напряженности, а именно:

\[Ф_E=\int\limits_S<\overrightarrow\cdot d\overrightarrow>\ \ \left(1.1\right),\ \]

Запишем выражение для нормали к поверхности сферы, в виде:

Готовые работы на аналогичную тему

В качестве основы для решения можно взять формулу для потока вектора напряженности в виде:

\[Ф_E=\overrightarrow\cdot S\overrightarrow=EScos\alpha \ \left(2.1\right),\]

Результирующая напряженность поля может быть найдена в соответствии с принципом суперпозиции полей двух зарядов, с учетом знаков.

Запишем выражение для модуля напряженности поля, которое создает первый заряд:

Для второго заряда:

Если мы ищем поток через сферу, которая имеет радиус R, то выражение (2.4) примет вид:

Площадь поверхности сферы (S) заданного радиуса равна:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 12 2021

Источник