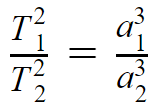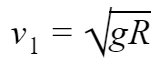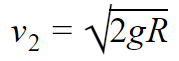Что такое полуось в астрономии

Большая полуось

Большая полуось — это один из основных геометрических параметров объектов, образованных посредством конического сечения.

Содержание

Эллипс

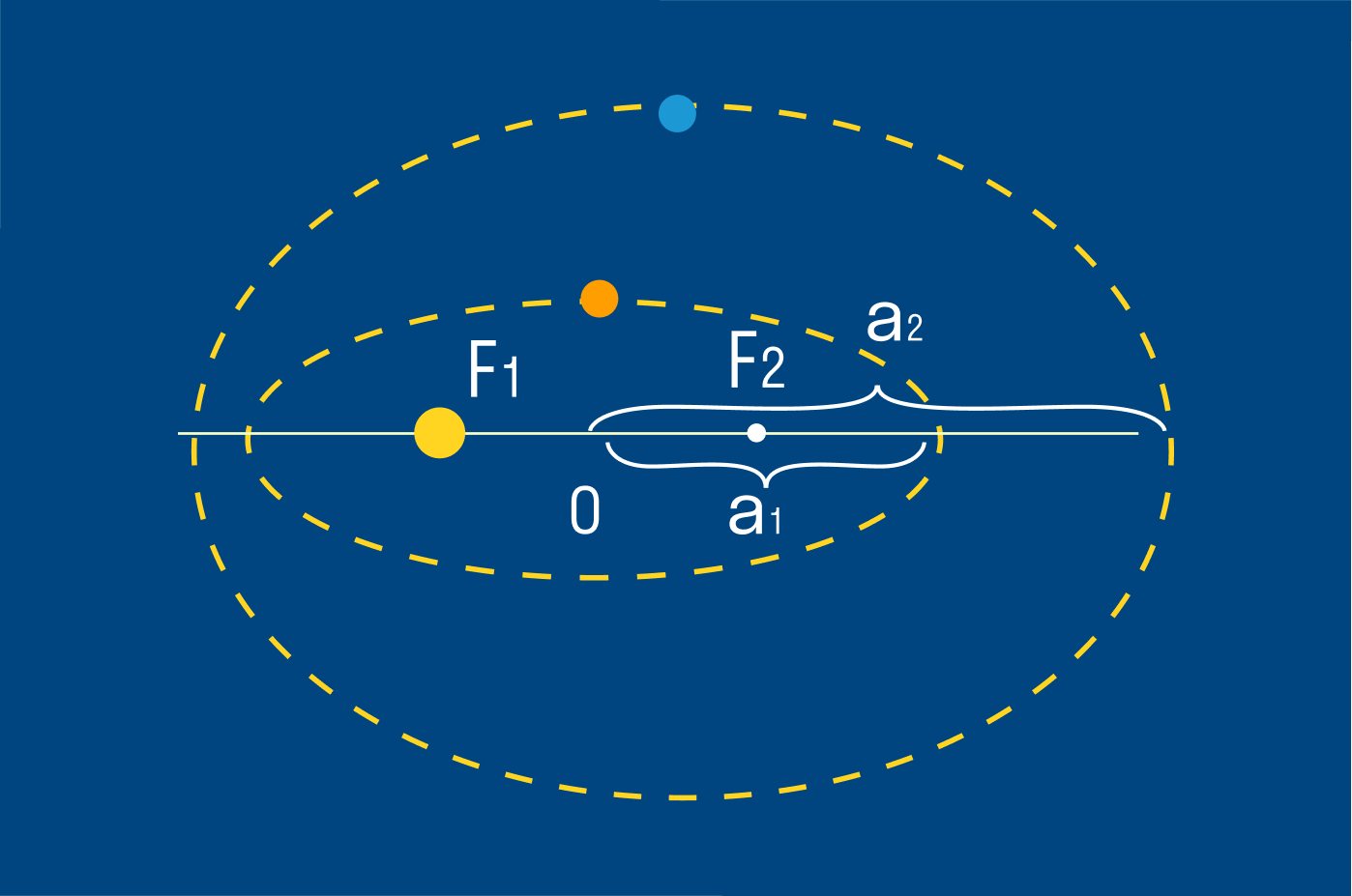
Большой осью эллипса называется его наибольший диаметр, прямая проходящая через центр и два фокуса. А большая полуось составляет половину этого расстояния, и таким образом, идёт от центра, через фокус, и на край эллипса. А под углом в 90° к большой полуоси располагается малая полуось — это минимальное расстояние от центра эллипса до его края. Для частного случая круга, большая и малая полуоси равны и являются радиусами. Таким образом, можно думать о большой и малой полуосях как о, своего рода, радиусах эллипса.

Длина большой полуоси связана с длиной малой полуоси через эксцентриситет и коническое сечение , следующим образом:

Большая полуось представляет собой среднее значение наибольшего и наименьшего расстояния от точки эллипса до его фокусов. Рассмотрим теперь уравнение в полярных координатах, с точкой в начале координат (полюс) и лучом, начинающейся из этой точки (полярная ось):

Получим средние значения и и большую полуось

Парабола

Параболу можно получить как предел последовательности эллипсов, где один фокус остаётся постоянным, а другой отодвигается в назад, сохраняя постоянным. Таким образом и стремятся к бесконечности, причём быстрее, чем .

Гипербола

Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:

Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:

.

Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы. [1]

Астрономия

Орбитальный период

В небесной механике орбитальный период обращения малых тел по эллиптической или круговой орбите вокруг более крупного центрального тела рассчитывается по формуле:

— это размер большой полуоси орбиты — это стандартный гравитационный параметр (en:standard gravitational parameter)

Следует обратить внимание, что в данной формуле для всех эллипсов период обращения определяется значением большой полуоси, независимо от эксцентриситета.

Для объектов Солнечной системы большая полуось связана с орбитальным периодом по третьему закону Кеплера.

— орбитальный период в годах; — большая полуось в астрономических единицах.

Это выражение является частным случаем общего решения задачи двух тел Исаака Ньютона:

— гравитационная постоянная — масса центрального тела — масса обращающегося вокруг него спутника. Как правило, масса спутника настолько мала по сравнению с массой центрального тела, что ею можно пренебречь. Поэтому, сделав соответствующие упрощения в этой формуле, получим данную формулу в упрощённом виде, который приведён выше.

Орбита движения спутника вокруг общего с центральным телом центра масс (барицентра), представляет собой эллипс. Большая полуось используется в астрономии всегда применительно к среднему расстоянию между планетой и звездой, в результате орбиты планет Солнечной системы приведены к гелиоцентрической системе, а не к системе движения вокруг центра масс. Эту разницу удобнее всего проиллюстрировать на примере системы Земля-Луна. Отношение масс в этом случае составляет 81,30059. Большая полуось геоцентрической орбиты Луны составляет 384400 км. В то время как расстояние до Луны относительно центра масс системы Земля-Луна составляет 379700 км, из-за влияния массы Луны центр масс находится не в центре Земли, а в 4700 км от него. В итоге средняя орбитальная скорость Луны относительно центра масс составляет 1,010 км/с, а средняя скорость Земли 0,012 км/с. А общая сумма этих скоростей даёт орбитальную скорость Луны 1,022 км/с; тоже самое значение можно получить, рассматривая движение Луны относительно центра Земли, а не центра масс.

Среднее расстояние

Часто говорят, что большая полуось является средним расстоянием между центральным и орбитальным телом. Это не совсем верно, так как под средним расстоянием можно понимать разные значения – в зависимости от величины, по которой производят усреднение:

Энергия; расчёт большой полуоси методом векторов состояния

В небесной механике большая полуось может быть рассчитана методом векторов орбитального состояния:

для эллиптических орбит

для гиперболической траектории

(стандартный гравитационный параметр), где:

— орбитальная скорость спутника, на основе вектора скорости, — вектор положения спутника в координатах системы отсчёта, относительно которой должны быть вычислены элементы орбиты (например, геоцентрический в плоскости экватора — на орбите вокруг Земли, или гелиоцентрический в плоскости эклиптики — на орбите вокруг Солнца), — гравитационная постоянная, и — массы тел.

Большая полуось рассчитывается на основе общей массы и удельной энергии, независимо от значения эксцентриситета орбиты.

См. также

Примечания

Ссылки

Это заготовка статьи о науке. Вы можете помочь проекту, исправив и дополнив её. Это примечание по возможности следует заменить более точным.

Классические	Наклонение · Долгота восходящего узла · Эксцентриситет · Аргумент перицентра · Большая полуось · Средняя аномалия на эпоху
Другие	Истинная аномалия · Малая полуось · Эксцентрическая аномалия · Средняя долгота · Истинная долгота · Период обращения

Небесная механика
Законы и задачи	Законы Ньютона • Закон всемирного тяготения • Законы Кеплера • Задача двух тел • Задача трёх тел • Гравитационная задача N тел • Задача Бертрана • Уравнение Кеплера
Небесная сфера	Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая • Международная небесная система координат • Сферическая система координат • Ось мира • Небесный экватор • Прямое восхождение • Склонение • Эклиптика • Равноденствие • Солнцестояние • Фундаментальная плоскость
Параметры орбит	Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра • Апоцентр и перицентр • Орбитальная скорость • Узел орбиты • Эпоха
Движение небесных тел	Движение Солнца и планет по небесной сфере • Эфемериды Конфигурации планет: противостояние • квадратура • парад планет • Кульминация • Сидерический период • Орбитальный резонанс • Период вращения • Предварение равноденствий • Синодический период • Сближение Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл • Покрытие • Прохождение • Либрация • Элонгация • Эффект Козаи • Эффект Ярковского • Эффект Джанибекова
Астродинамика
Космический полёт	Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая Формула Циолковского • Гравитационный манёвр • Гомановская траектория • Метод оскулирующих элементов • Приливное ускорение • Изменение наклонения орбиты • Стыковка • Точки Лагранжа • Эффект «Пионера»
Орбиты КА	Геостационарная орбита • Гелиоцентрическая орбита • Геосинхронная орбита • Геоцентрическая орбита • Геопереходная орбита • Низкая опорная орбита • Полярная орбита • Тундра-орбита • Солнечно-синхронная орбита • Молния-орбита • Оскулирующая орбита

Полезное

Смотреть что такое «Большая полуось» в других словарях:

большая полуось — didysis pusašis statusas T sritis fizika atitikmenys: angl. semi major axis vok. große Halbachse, f rus. большая полуось, f pranc. demi grand axe, m … Fizikos terminų žodynas

большая полуось а — 3.2 большая полуось а: Максимальный радиус эллипсоида. Примечание Для эллипсоида, представляющего Землю, это радиус экватора. Источник: ГОСТ Р 52572 2006: Географические информационные системы. Координатная основа. Общие требования … Словарь-справочник терминов нормативно-технической документации

большая полуось эллипсоида — 2.1.1 большая полуось эллипсоида : Параметр, характеризующий размер эллипсоида. Источник … Словарь-справочник терминов нормативно-технической документации

Большая полуось орбиты — величина (элемент орбиты (См. Элементы орбиты)), определяющая вместе с эксцентриситетом орбиты (См. Эксцентриситет орбиты) её размеры … Большая советская энциклопедия

Большая — постоянное или часто повторяющееся воздействие жидкостей на покрытие пола. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зданий с применением материалов фирмы «Хенкель Баутехник» … Словарь-справочник терминов нормативно-технической документации

Большая комета 1811 года — C/1811 F1 (Большая комета) Открытие Первооткрыватель: Оноре Флагерье Дата открытия: 25 марта 1811 Альтернативные обозначения: 1811 I 1811a Характеристики орбиты Афелий: 424 а. е. Перигелий: 1,035412 а. е. Большая полуось … Википедия

Большая мартовская комета 1843 года — C/1843 D1 (Большая мартовская комета) Зарисовка Большой мартовской кометы 1843, сделанная в Тасмании. Открытие Дата открытия: 5 февраля 1843 Альтернативные обозначения: 1843 I 1843a Характеристики орбиты Афелий: 129 а. е … Википедия

Большая комета 1843 года — C/1843 D1 (Большая мартовская комета) Зарисовка Большой мартовской кометы 1843, сделанная в Тасмании. Открытие Дата открытия: 5 февраля 1843 Альтернативные обозначения: 1843 I 1843a Характеристики орбиты Афелий: 129 а. е … Википедия

Большая комета 1965 года — C/1965 S1 (Икея Секи) Открытие Первооткрыватель: Каору Икея, Цуоми Секи Дата открытия: 18 сентября 1965 Альтернативные обозначения: 1965 VIII; 1965f Характеристики орбиты Эпоха: 7 октября 1965 … Википедия

Малая полуось — Не следует путать с термином «Эллипсис». Эллипс и его фокусы Эллипс (др. греч. ἔλλειψις недостаток, в смысле недостатка эксцентриситета до 1) геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1… … Википедия

Источник

Закон Кеплера

Форма Земли

Сейчас нам сложно представить, что раньше люди верили, будто Земля плоская. У греков, например, плоскость просто парила в воздухе и была окружена ледниками. А в Индии верили, что планета покоится на трех слонах, которые стоят на черепахе. Впрочем, кое-кто до сих пор так думает. Доказательств того, что наша планета на самом деле не плоская — много, но вот вам парочка, чтобы можно было поддержать светскую беседу.

Гравитация

Гравитация всегда притягивает все в сторону центра масс. Наша Земля — сферической формы, а центр масс сферы находится как раз в ее центре.

Гравитация притягивает все объекты на поверхности в направлении ядра Земли, то есть вниз, независимо от их местоположения — что мы всегда и наблюдаем.

Если представить, что Земля плоская, то гравитация должна будет притягивать все, что на поверхности, к центру плоскости. То есть если вы окажетесь у края плоской Земли, гравитация будет тянуть вас не вниз, а к центру диска.

Чтобы доказать свою точку зрения, сторонникам плоской Земли придется поискать на планете место, где вещи падают не вниз, а вбок.

Если бы Земля была плоской, да еще и со слонами и черепахой, то при лунном затмении мы бы видели не равномерно растущую тень, а примерно такую картину:

Но, пожалуй, это сильно отличается от реальности.

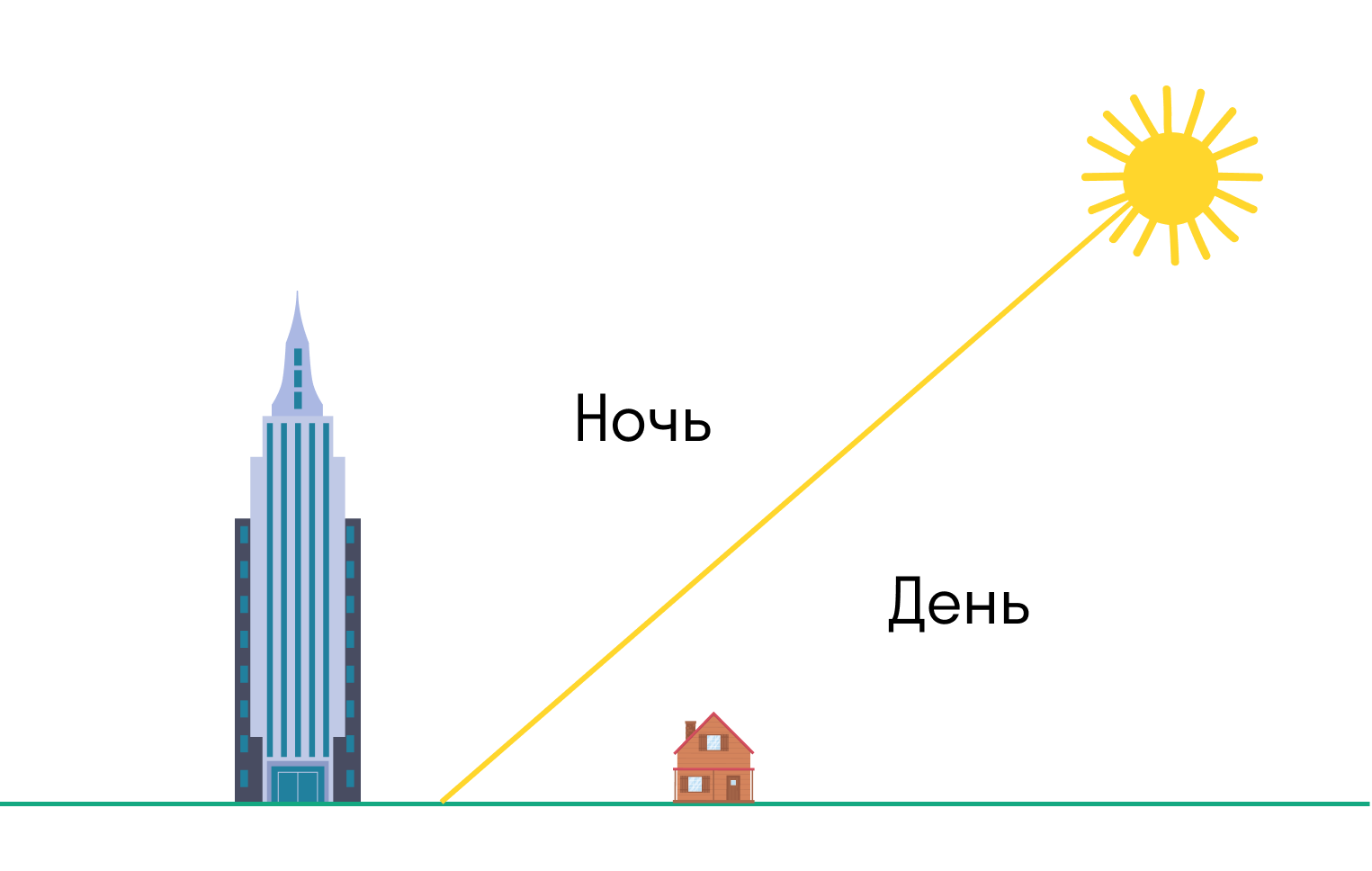
На плоскую Землю свет от Солнца падал бы, как свет от фонаря. То есть высокие объекты в противоположном от Солнца направлении после заката оставались бы в тени.

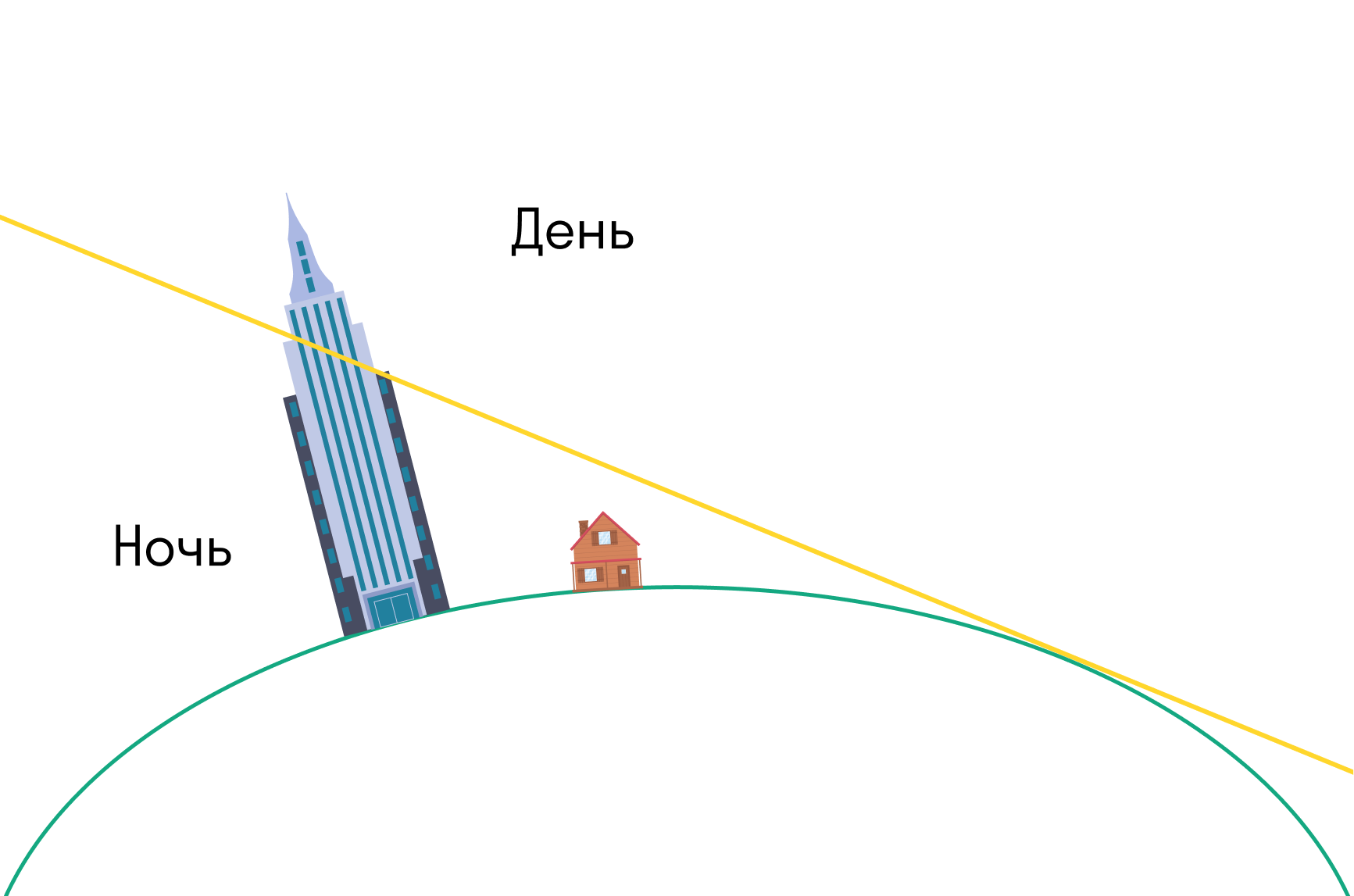
А на шарообразной Земле небоскребы или горы будут освещены Солнцем после заката или перед рассветом.

Именно это вы увидите, если застанете рассвет или закат в горах — или посмотрите на фотографии.

Окей, Земля все-таки не плоская — с этим разобрались. Но и шаром ее назвать нельзя: Земля имеет форму эллипсоида.

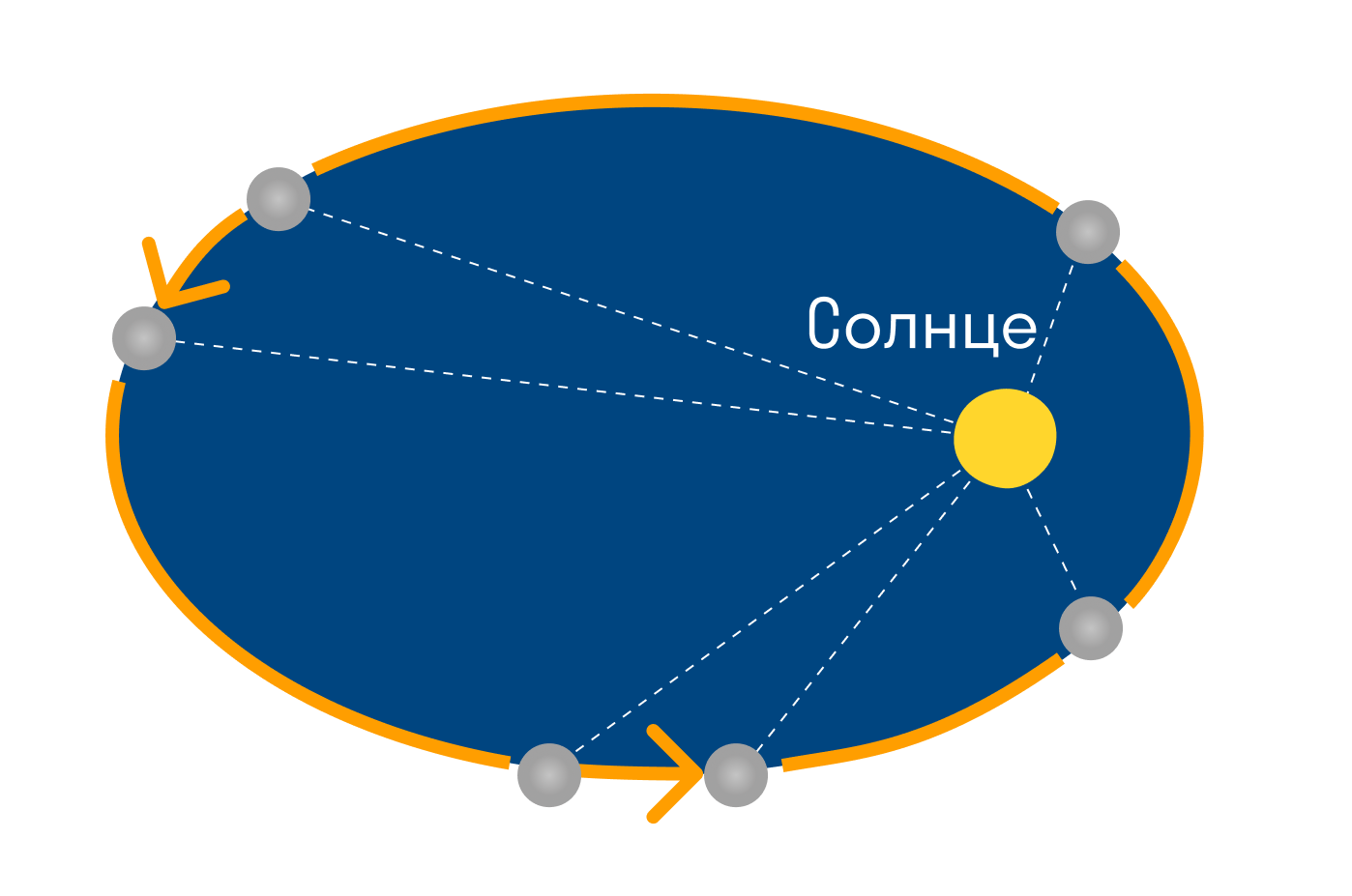
Эллипсоид — это такой приплюснутый шар, в сечении у которого эллипс. Именно по траектории эллипса вращаются все спутники.

Эллипс

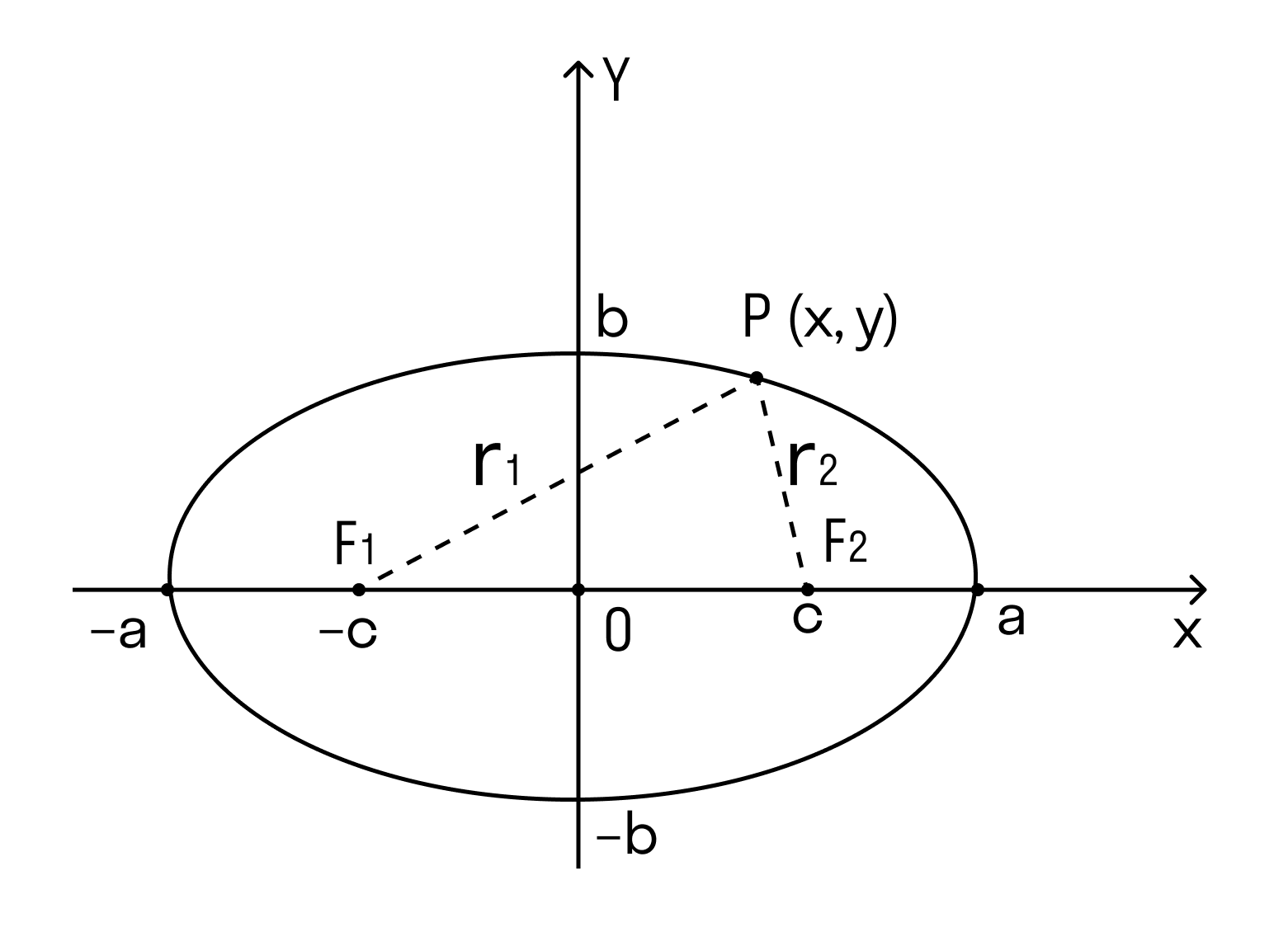
Эллипс — это замкнутая прямая на плоскости, частный случай овала. У эллипса две оси симметрии — горизонтальная и вертикальная, которые состоят из двух полуосей.

А еще у эллипса два фокуса — это такие точки, сумма расстояний от которых до любой точки P(x,y) является постоянной величиной.

Эллипс

F₁ и F₂ — фокусы

с — половина расстояния между F₁ и F₂

a — большая полуось

b — малая полуось

r₁ и r₂ — фокальные радиусы

Теперь мы знаем все необходимые понятия, чтобы разобраться, в чем состоят законы Кеплера.

Первый закон Кеплера

Каждая планета солнечной системы вращается вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.

Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка B траектории называется перигелием, а точка A, наиболее удаленная от Солнца — афелием.

Первый закон Кеплера достаточно простой, но важный, так как в свое время он сильно продвинул астрономию. До этого открытия астрономы считали, что планеты движутся исключительно по круговым орбитам. Если же наблюдения противоречили этому убеждению, ученые дополняли главное круговое движение малыми кругами, которые планеты описывали вокруг точек основной круговой орбиты. Кеплер получил доступ к огромной базе наблюдений Тихо Браге и, изучив их, перешагнул старые идеи.

Второй закон Кеплера (закон площадей)

Радиус-вектор планеты описывает в равные промежутки времени равные площади.

Каждая планета перемещается в плоскости, проходящей через центр Солнца. В одно и то же время радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Таким образом, тела движутся вокруг Солнца неравномерно: в перигелии они имеют максимальную скорость, а в афелии — минимальную.

На практике это можно заметить по движению Земли. Ежегодно в начале января наша планета проходит через перигелий и перемещается быстрее. Из-за этого движение Солнца по эклиптике также происходит быстрее, чем в другое время года. В начале июля Земля движется через афелий, из-за чего Солнце по эклиптике перемещается медленнее. Поэтому световой день летом длиннее, чем зимой.

Третий закон Кеплера

Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.

Согласно третьему закону Кеплера, между периодом обращения планет вокруг Солнца и средним расстоянием от Солнца до планеты или спутника устанавливается связь. Этот закон выполняется как для планет, так и для спутников с погрешно­стью менее 1%.

Третий закон Кеплера

T₁ и T₂ — периоды обращения двух планет [c]

a₁ и a₂ — большие полуоси орбит планет [м]

На основании этого закона можно вычис­лить продолжительность года (времени полного оборота вокруг Солнца) любой планеты, если известно ее расстояние до Солнца.

Также можно проделать обратное — рассчитать орбиту, зная период обращения.

Закон всемирного тяготения

Законы Кеплера — это результаты наблюдений и обобщений. Теоретически их обосновал Исаак Ньютон в законе всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

Ньютон был первым исследователем, который пришел к выводу, что между любыми телами в космосе действуют гравитационные силы, и именно они определяют характер движения этих тел.

Первая и вторая космические скорости

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

В серии книг Дугласа Адамса «‎Автостопом по Галактике»‎ говорится, что летать — это просто промахиваться мимо Земли. Если ты промахнулся мимо Земли и достиг первой космической скорости 7,9 км/с, то ты стал искусственным спутником нашей планеты.

Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него это получалось, аппарат должен иметь начальную скорость, которая равна или больше первой космической.

Первая космическая скорость

v₁ — первая космическая скорость [м/с]

g — ускорение свободного падения на данной планете [м/с 2 ]

R — радиус планеты [м]

Есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.

Вторая космическая скорость

v₂ — вторая космическая скорость [м/с]

g — ускорение свободного падения на данной планете [м/с 2 ]

Источник

• ← что такое фуфыкс процессор
• какая буква флажковой азбуки изображена на рисунке →