Что такое положение равновесия
Равновесие тел. Виды равновесия тел
Виды равновесия тел
Это происходит, если при небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. Например, шарик, лежащий на дне сферического углубления (рис.1 а).
В данном случае при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Примером может служить шарик, находящийся в верхней точке выпуклой сферической поверхности (ри.1 б).
В этом случае при небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю. Например, шарик, лежащий на плоской поверхности (рис.1,в).
Рис.1. Различные типы равновесия тела на опоре: а) устойчивое равновесие; б) неустойчивое равновесие; в) безразличное равновесие.
Статическое и динамическое равновесие тел
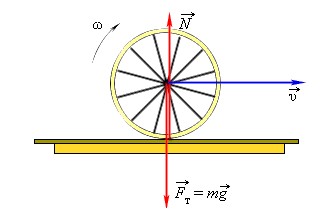
Если в результате действия сил тело не получает ускорения, оно может находиться в состоянии покоя или двигаться равномерно прямолинейно. Поэтому можно говорить о статическом и динамическом равновесии.
Динамическое равновесие — это такое равновесие, когда по действием сил тело не изменяет своего движения.
В состоянии статического равновесия находится подвешенный на тросах фонарь, любое строительное сооружение. В качестве примера динамического равновесия можно рассматривать колесо, которое катится по плоской поверхности при отсутствии сил трения.
Равновесие
Понятие равновесия — одно из самых универсальных в естественных науках. Оно применимо к любой системе, будь то система планет, движущихся по стационарным орбитам вокруг звезды, или популяция тропических рыбок в лагуне атолла. Но проще всего понять концепцию равновесного состояния системы на примере механических систем. В механике считается, что система находится в равновесии, если все действующие на нее силы полностью уравновешены между собой, то есть гасят друг друга. Если вы читаете эту книгу, например, сидя в кресле, то вы как раз и находитесь в состоянии равновесия, поскольку сила земного притяжения, тянущая вас вниз, полностью компенсирована силой давления кресла на ваше тело, действующей снизу вверх. Вы не проваливаетесь и не взлетаете именно потому, что пребываете в состоянии равновесия.
Различают три типа равновесия, соответствующие трем физическим ситуациям.
Устойчивое равновесие
Именно его большинство людей обычно и понимают под «равновесием». Представьте себе шар на дне сферической чаши. В состоянии покоя он находится строго в центре чаши, где действие силы гравитационного притяжения Земли уравновешено силой реакции опоры, направленной строго вверх, и шар покоится там подобно тому, как вы покоитесь в своем кресле. Если сместить шар в сторону от центра, откатив его вбок и вверх в направлении края чаши, то, стоит его отпустить, как он тут же устремится обратно к самой глубокой точке в центре чаши — в направлении положения устойчивого равновесия.
Вы, сидя в кресле, находитесь в состоянии покоя благодаря тому, что система, состоящая из вашего тела и кресла, находится в состоянии устойчивого равновесия. Поэтому при изменении каких-то параметров этой системы — например, при увеличении вашего веса, если, предположим, вам на колени сел ребенок, — кресло, будучи материальным объектом, изменит свою конфигурацию таким образом, что сила реакции опоры возрастет, — и вы останетесь в положении устойчивого равновесия (самое большее, что может произойти, — подушка под вами промнется чуть глубже).
В природе имеется множество примеров устойчивого равновесия в различных системах (и не только механических). Рассмотрим, например, отношения хищник—жертва в экосистеме. Соотношение численностей замкнутых популяций хищников и их жертв достаточно быстро приходит в равновесное состояние — столько-то зайцев в лесу из года в год стабильно приходится на столько-то лис, условно говоря. Если по каким-либо причинам численность популяции жертв резко изменяется (из-за всплеска рождаемости зайцев, например), экологическое равновесие будет очень скоро восстановлено за счет быстрого прироста поголовья хищников, которые начнут истреблять зайцев ускоренными темпами, пока не приведут поголовье зайцев в норму и не начнут сами вымирать от голода, приводя в норму и собственное поголовье, в результате чего численности популяций и зайцев, и лис придут к норме, которая наблюдалась до всплеска рождаемости у зайцев. То есть в устойчивой экосистеме также действуют внутренние силы (хотя и не в физическом понимании этого слова), стремящиеся вернуть систему в состояние устойчивого равновесия в случае отклонения системы от него.
Аналогичные эффекты можно наблюдать и в экономических системах. Резкое падение цены товара приводит к всплеску спроса со стороны охотников за дешевизной, последующему сокращению товарных запасов и, как следствие, росту цены и падению спроса на товар — и так до тех пор, пока система не вернется в состояние устойчивого ценового равновесия спроса и предложения. (Естественно, в реальных системах, и в экологических, и в экономических, могут действовать внешние факторы, отклоняющие систему от равновесного состояния — например, сезонный отстрел лис и/или зайцев или государственное ценовое регулирование и/или квотирование потребления. Такое вмешательство приводит к смещению равновесия, аналогом которого в механике будет, например, деформация или наклон чаши.)
Неустойчивое равновесие
Не всякое равновесие, однако, является устойчивым. Представьте себе шар, балансирующий на лезвии ножа. Направленная строго вниз сила земного притяжения в этом случае, очевидно, также полностью уравновешена направленной вверх силой реакции опоры. Но стоит отклонить центр шара в сторону от точки покоя, приходящейся на линию лезвия хоть на долю миллиметра (а для этого достаточно мизерного силового воздействия), как равновесие будет мгновенно нарушено и сила земного притяжения начнет увлекать шар всё дальше от него.
Примером неустойчивого природного равновесия служит тепловой баланс Земли при смене периодов глобального потепления новыми ледниковыми периодами и наоборот (см. Циклы Миланковича). Среднегодовая температура поверхности нашей планеты определяется энергетическим балансом между суммарным солнечным излучением, достигающим поверхности, и суммарным тепловым излучением Земли в космическое пространство. Неустойчивым этот тепловой баланс становится следующим образом. В какую-то зиму выпадает больше снега, чем обычно. На следующее лето тепла не хватает, чтобы растопить излишки снега, и лето оказывается также холоднее обычного вследствие того, что из-за переизбытка снега поверхность Земли отражает обратно в космос большую долю солнечных лучей, чем прежде. Из-за этого следующая зима оказывается еще более снежной и холодной, чем предыдущая, а следующим за ней летом на поверхности остается еще больше снега и льда, отражающего солнечную энергию в космос. Нетрудно увидеть, что чем больше такая глобальная климатическая система отклоняется от исходной точки теплового равновесия, тем быстрее нарастают процессы, уводящие климат еще дальше от нее. В конечном итоге, на поверхности Земли в приполярных областях за долгие годы глобального похолодания образуются многокилометровые напластования ледников, которые неумолимо продвигаются в направлении всё более низких широт, принося с собой на планету очередной ледниковый период. Так что трудно себе представить более шаткое равновесие, чем глобально-климатическое.
Особого упоминания заслуживает разновидность неустойчивого равновесия, называющаяся метастабильным, или квазиустойчивым равновесием. Представьте себе шар в узкой и неглубокой канавке — например, на повернутом острием вверх лезвии фигурного конька. Незначительное — на миллиметр-другой — отклонение от точки равновесия приведет к возникновению сил, которые вернут шар в равновесное состояние в центре канавки. Однако уже чуть большей силы хватит для того, чтобы вывести шар за пределы зоны метастабильного равновесия, и он свалится с лезвия конька. Метастабильные системы, как правило, обладают свойством пребывать какое-то время в состоянии равновесия, после чего «срываются» из него в результате какой-либо флуктуации внешних воздействий и «сваливаются» в необратимый процесс, характерный для нестабильных систем.
Типичный пример квазиустойчивого равновесия наблюдается в атомах рабочего вещества некоторых типов лазерных установок. Электроны в атомах рабочего тела лазера занимают метастабильные атомные орбиты и остаются на них до пролета первого же светового кванта, который «сбивает» их с метастабильной орбиты на более низкую стабильную, испуская при этом новый квант света, когерентный пролетающему, который, в свою очередь, сбивает с метастабильной орбиты электрон следующего атома и т. д. В результате запускается лавинообразная реакция излучения когерентных фотонов, образующих лазерный луч, которая, собственно, и лежит в основе действия любого лазера.
Безразличное равновесие
Промежуточный случай между устойчивым и неустойчивым равновесием — так называемое безразличное равновесие, при котором любая точка системы является точкой равновесия, и отклонение системы от исходной точки покоя ничего не изменяет в раскладе сил внутри нее. Представьте себе шар на абсолютно гладком горизонтальном столе — куда бы вы его ни сместили, он останется в состоянии равновесия.
Условия равновесия тел
Равновесие тела
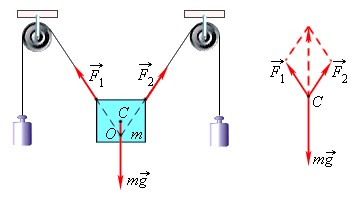
Тело находится в состоянии покоя (или движется равномерно и прямолинейно), если векторная сумма всех сил, действующих на него, равна нулю. Говорят, что силы уравновешивают друг друга. Когда мы имеем дело с телом определенной геометрической формы, при вычислении равнодействующей силы можно все силы прикладывать к центру масс тела.
Условие равновесия тел
Чтобы тело, которое не вращается, находилось в равновесии, необходимо, чтобы равнодействующая всех сил, действующий на него, была равна нулю.
Равновесие вращающегося тела. Правило моментов
Условия равенства нулю равнодействующей всех сил недостаточно, если тело может вращаться вокруг некоторой оси.
Определение. Правило моментов
Если алгебраическая сумма всех моментов, приложенных к телу относительно неподвижной оси вращения, равна нулю, то тело находится в состоянии равновесия.
В общем случае для равновесия тел необходимо выполнение двух условий: равенство нулю равнодействующей силы и соблюдение правила моментов.
Безразличное, устойчивое и неустойчивое равновесие
В механике есть разные виды равновесия. Так, различают устойчивое и неустойчивое, а также безразличное равновесие.
Линия, проведенная из центра масс башни пересекает основание приблизительно в 2,3 м от его центра.
Равновесие тел
Урок 35. Физика 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Равновесие тел»
Все вы отлично знаете значение слова «равновесия». Например, в равновесии могут находиться весы, равновесие может держать едущий велосипедист или бегущий человек.
В физике под равновесием понимается состояние покоя. Например, дом и большинство его частей покоятся относительно Земли, несмотря на то, что этот дом находится под воздействием различных сил. Любое реальное тело деформируется под воздействием тех или иных сил. Если эти силы вызывают значительные деформации, такие, как растяжение пружины или изгиб металлической линейки, ни в коем случае нельзя считать, что эти тела находятся в равновесии. Если тело двигается и при этом существенно деформируется, то, по мере его движения, меняется его форма и, некоторые силы начинают действовать на данное тело по-разному. Кроме того, с изменением формы постоянно меняется модуль и направление внутренних сил. Вы можете себе представить, насколько сложно описать такое движение математически.
Однако, во многих случаях на практике эти деформации незначительны. В таких случаях мы можем говорить о равновесии абсолютно твердых тел, тем самым пренебрегая их деформацией.
Скажем, бревенчатый дом, находясь на Земле, разумеется, находится в состоянии равновесия.
Каждое бревно, балка или кусок шифера не двигаются относительно Земли. Хотя, если присмотреться, то можно обнаружить, что некоторые бревна деформировались под действием веса других бревен. Мы можем увидеть какие-то незначительные изменения формы бревен или досок. Но, как правило, этими изменениями можно пренебречь. Поэтому, дом можно считать абсолютно твердым телом, находящимся в равновесии.
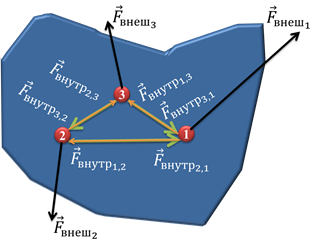
Возьмем некое произвольное тело и выберем несколько произвольных элементов этого тела. На каждый элемент тела может действовать несколько внешних и несколько внутренних сил.
В данном примере мы будем рассматривать равнодействующие внешних сил и равнодействующие внутренних сил. Черными стрелочками обозначены равнодействующие некоторых сил, которые действуют извне на различные элементы тела. Оранжевыми стрелочками обозначены воздействия элементов тела друг на друга посредством внутренних сил. Но, как вы знаете, всякое действие имеет противодействие. Противодействие каждого элемента обозначено зелеными стрелочками. Так вот, если тело находится в состоянии покоя, то ускорение каждого элемента должно быть равно нулю. Следовательно, равнодействующая сила, действующая на каждый из элементов, равна нулю.
Таким образом, можно утверждать, что если равнодействующая сила внутренних и внешних сил, действующих на каждый элемент тела, равна нулю, то тело находится в равновесии.
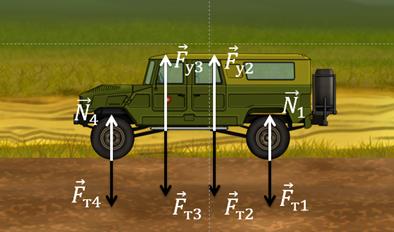
Рассмотрим несколько простых примеров. На каждую точку припаркованной машины действует сила тяжести. Эту силу тяжести уравновешивает реакция опоры в тех точках, которые взаимодействуют с опорой. В точках, которые не соприкасаются с опорой, силу тяжести уравновешивает сила упругости, препятствующая деформации.
В действительности мы знаем, что если машину как следует нагрузить, то она немного просядет, но этой деформацией можно пренебречь, поскольку изменение формы машины весьма незначительно.
Также можно привести в пример лодку, находящуюся на воде. При мертвом штиле и выключенном моторе лодка будет находиться в равновесии. На каждую её точку будет действовать сила тяжести и сила Архимеда. Сумма этих сил будет равна нулю.
Раздел механики, изучающий равновесие и условия равновесия абсолютно твердых тел, называется статикой. В этом разделе мы будем считать все тела абсолютно твердыми и рассматривать случаи, когда эти тела находятся в состоянии покоя.
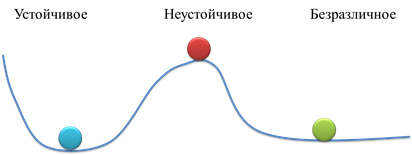
Необходимо отметить, что существует три вида равновесия: устойчивое, неустойчивое и безразличное.
Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.
Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.
Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.
Условия равновесия в механике
Равновесие в статике – это отсутствие движения. Чтобы объект находился в равновесии, нужно, чтобы выполнялись некоторые условия, рассмотрим их.
Условие равновесия материальной точки
Чтобы материальная точка находилась в равновесии, нужно, чтобы она не двигалась поступательно.
Примечания:
Материальная точка будет находиться в равновесии, когда выполняются два условия:
1. Векторная cумма сил, действующих на точку, должна равняться нулю.
Примечание: При выполнении этого условия, точка будет либо покоиться, либо двигаться вдоль прямой с одной и той же скоростью. Это следует из первого закона Ньютона.
2. Систему отсчета дополнительно выберем так, чтобы координаты точки в системе не менялись при выполнении условия 1.
Примечание: Такая система отсчета будет называться инерциальной, а точка будет покоиться относительно этой системы.
Условие равновесия тела
Чтобы тело находилось в равновесии, нужно, чтобы оно не двигалось поступательно и не вращалось.
Примечание: Тело, состоящее из нескольких точек, может вращаться вокруг оси, проходящей через центр этого тела. Поэтому, для тела условия равновесия нужно дополнить еще одним пунктом. Таким образом, получим три условия.
1. Алгебраическая cумма моментов сил, действующих на тело, должна равняться нулю.
\[ \large \boxed < M_<1>+ M_ <2>+ M_ <3>+ \ldots + M_
Примечания:
2. Векторная cумма сил, действующих на тело, должна равняться нулю.
Примечания:
3. Систему отсчета выберем так, чтобы координаты всех точек тела не менялись в ней при равенстве нулю векторной суммы сил.
Условия равновесия применяются для решения задач статики, связанных с моментами сил.
Виды равновесия
Различают такие виды равновесия:
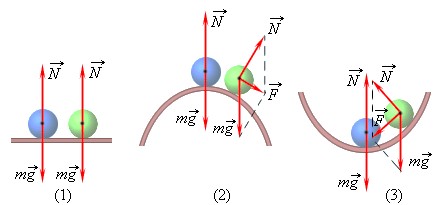
Рассмотрим однородный шар (или, например, мяч), который покоится (рис. 1) на горке – а), на горизонтальном участке – б), и в ложбинке – в).
Неустойчивое равновесие
На вершине горы мяч находится в неустойчивом равновесии, потому, что стоит нам подтолкнуть мяч и, он скатится с горки (рис. 1а).
Равновесие неустойчивое:
при малом отклонении
потенциальная энергия тела уменьшается
силы и моменты сил
еще больше уводят тело от положения равновесия.
В состоянии неустойчивого равновесия потенциальная энергия тела максимальна!
Безразличное равновесие
На горизонтальном участке мяч будет покоиться в любом месте, в которое мы его поместим (рис. 1б). Подтолкнем мяч, он перекатится в другое положение и там будет оставаться в безразличном равновесии.
Если потенциальная энергия тела при его перемещении из одной точки пространства в другую точку остается постоянной, равновесие можно назвать безразличным.
Устойчивое равновесие
Мяч находится в ложбинке в устойчивом равновесии (рис. 1в). Легонько подтолкнув мяч, мы выведем его из равновесия, но через непродолжительное время мяч опять вернется в ложбинку.
Равновесие устойчивое:
при малом отклонении от равновесия
потенциальная энергия тела увеличивается
силы и моменты сил
возвращают тело в положение равновесия.
Примечание: Потенциальная энергия тела будет минимально возможной, когда тело находится в устойчивом равновесии!
Равновесие тела, могущего вращаться вокруг горизонтальной оси
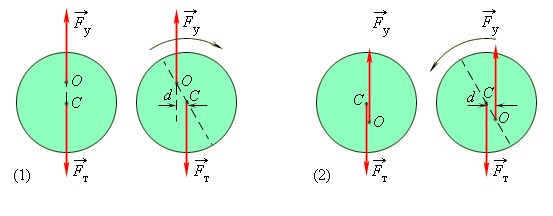
Рассмотрим однородный шар, изготовленный, к примеру, из пенопласта. Проткнем его спицей, после закрепим ее горизонтально, подобно перекладине на двух опорах (рис. 2).
Спица будет являться неподвижной осью вращения.
Рассмотрим три случая для тела, могущего вращаться вокруг оси. Ось вращения
Примечание для случаев устойчивого и неустойчивого равновесия:
центр масс расположен на вертикальной линии (пунктир на рисунках 2б и 2в), проходящей через ось вращения.
Вокруг неподвижной оси может вращаться любое тело, в том числе, продолговатое, например, рычаг. В задачах статики для него применяют условия равновесия рычага.
Тело опирается на площадь поверхности
Условие равновесия для такого тела:
Проекция центра масс должна лежать внутри площади основания.
Допустим, зодчий захотел построить наклонную башню. Заменим для упрощения башню однородным наклонным цилиндром (рис. 3).
Упадет ли наклонная башня?
На рисунке 3а проекция центра масс попадает внутрь площади основания. Поэтому, башня, обладающая таким наклоном, не упадет.
Если центр масс выйдет за пределы площади, на которую тело опирается, то башня опрокинется (рис 3б).
Примечание: Башня своим весом давит на площадь основания – круг. Сила давления распределяется по всему основанию тела.