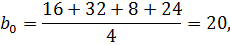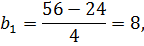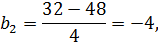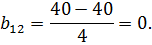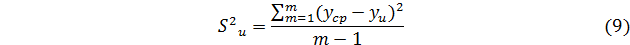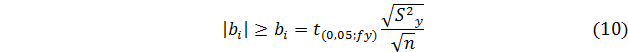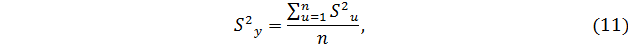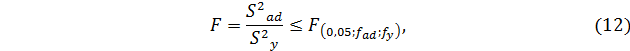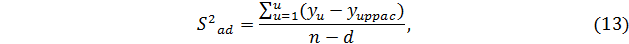Что такое полный факторный эксперимент

Теория Планирования Эксперимента

Главная

Полный факторный эксперимент

Нетрудно написать все сочетания уровней в экспе­рименте с двумя факторами. Напомним, что в планиро­вании эксперимента используются кодированные значения факторов: +1 и –1 (часто для простоты записи единицы опускают). Условия эксперимента можно записать в виде таблицы, где строки соответствуют различным опытам, а столбцы – значениям факторов. Будем называть такие таблицы матрицами планирования эксперимента.

Матрица планирования для двух факторов приведена ниже

Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку – вектор-строкой. Таким образом, мы имеем 2 вектор-столбца независимых переменных и один вектор-столбец парамет­ра оптимизации.

Если для двух факторов все возможные комбинации уровней легко найти прямым перебором (или просто запомнить), то с ростом числа факторов возникает необ­ходимость в некотором приеме построения матриц. Из многих возможных обычно используется три приема, основанные на переходе от матриц меньшей размерности к матри­цам большей размерности. Рассмотрим первый. При добав­лении нового фактора каждая комбинация уровней исход­ного плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Отсюда естественно появляется прием: записать исходный план для одного уровня нового фактора, а затем повторить его для другого уровня. Вот как это выглядит при переходе от экспери­мента 2 2 к 2 3 :

Этот прием распространяется на построение матриц любой размерности.

Рассмотрим второй прием. Для этого введем правило перемножения столбцов матрицы. При построчном перемно­жении двух столбцов матрицы произведение единиц с одноименными знаками дает +1, а с разноименными –1. Воспользовавшись этим правилом, получим для случая, который мы рассматриваем, вектор-столбец произведения x ₁ x ₂ в исходном плане. Далее повторим еще раз исходный план, а у столбца произведений знаки поменяем на обрат­ные. Этот прием тоже можно перенести на построение матриц любой размерности, однако он сложнее, тем первый.

Третий прием основан на правиле чередования знаков. В первом столбце знаки меняются поочередно, во втором столбце они чередуются через два, в третьем – через 4, в четвертом – через 8 и т. д. по степеням двойки.

Свойства полного факторного эксперимента типа 2 k

Мы научились строить матрицы планирования полных факторных экспериментов с факторами на двух уровнях. Теперь выясним, какими общими свойствами эти матрицы обладают независимо от числа факторов. Говоря о свойствах матриц, мы имеем в виду те из них, которые определяют качество модели. Ведь эксперимент и плани­руется для того, чтобы получить модель, обладающую некоторыми оптимальными свойствами. Это значит, что оценки коэффициентов модели должны быть наилучшими и что точность предсказания параметра оптимизации не должна зависеть от направления в факторном пространстве, ибо заранее неясно, куда предстоит двигаться в поисках оптимума.

Второе свойство – так называемое условие нормировки – формулируется следующим образом: сумма квадратов элементов каждого столбца равна числу опытов, или 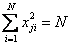. Это следствие того, что значения факторов в матрице задаются +1 и –1.

Это свойства отдельных столбцов матрицы планирования. Теперь остановимся на свойстве совокупности столбцов. Сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю, или

.

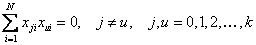
Это важное свойство называется ортогональностью матрицы планирования.

Последнее, четвертое свойство называется ротатабельностью, т. е. точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.

Полный факторный эксперимент и математическая модель

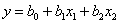
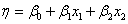
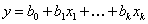
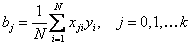
Для движения к точке оптимума нам нужна линейная модель . Наша цель – найти по результатам эксперимента значения неизвестных коэффициентов модели. До сих пор, говоря о линейной модели, мы не останавливались на важном вопросе о статистической оценке ее коэффициентов. Теперь необходимо сделать ряд замечаний по этому поводу. Можно утверждать, что эксперимент проводится для проверки гипотезы о том, что линейная модель адекватна. Греческие буквы использованы для обозначения «истинных» генеральных значений соответствующих неизвестных. Эксперимент, содержащий конечное число опытов, позволяет только получить выборочные оценки для коэффициентов уравнения . Их точность и надежность зависят от свойств выборки и нуждаются в статистической проверке. Как производится такая проверка, будет показано ниже. А пока займемся вычислением оценок коэффициентов. Их можно вычислить по простой формуле

,

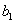
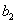
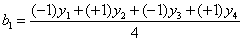
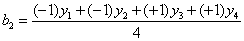
обоснование которой будет приведено ниже. Воспользуемся этой формулой для подсчёта коэффициентов и :

,

.

Теперь у нас есть все необходимое, чтобы найти неизвестные коэффициенты линейной модели

.

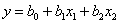
Коэффициенты при независимых переменных указывают на силу влияния факторов. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет знак плюс, то с увеличением зна­чения фактора параметр оптимизации увеличивается, а если минус, то уменьшается. Величина коэффициента соответ­ствует вкладу данного фактора в величину параметра опти­мизации при переходе фактора с нулевого уровня на верх­ний или нижний.

Иногда у добно оценивать вклад фактора при переходе от нижнего уровня к верхнему уровню. Вклад, определенный таким образом, называется вкладом фактора (иногда его называют основным или главным эффектом). Он численно равен удвоенному коэффициенту. Для качественных факторов, варьируемых на двух уровнях, основной уровень не имеет физического смысла. Поэтому понятие «эффект фактора» является здесь естественным.

Планируя эксперимент, на первом этапе мы стремимся получить линейную модель. Однако у нас нет гарантии, что в выбранных интервалах варьирования процесс описывается линейной моделью. Существуют способы проверки пригодности линейной модели (проверка адекватности). А если модель нелинейна, как количественно оценить нелинейность, пользуясь полным факторным экспериментом?

Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор. В этом случае гово­рят, что имеет место эффект взаимодействия двух факторов. Полный факторный эксперимент позволяет количественно оценивать эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, получить стол­бец произведения двух факторов. При вычислении коэффициента, соответствующего эффекту взаимодействия, с новым вектор-столбцом можно обращаться так же, как с вектор-столбцом любого фактора. Для полного факторного эксперимента 2 2 матрица планирования с учетом эффекта взаимодействия будет иметь вид

Источник

Полный факторный эксперимент

Полный факторный эксперимент (ПФЭ) – совокупность нескольких измерений, удовлетворяющих следующим условиям:

Преимуществами полного факторного эксперимента являются

Содержание

Предварительные сведения

Оценка параметров системы

В практической деятельности часто требуется оценить параметры некоторой системы, то есть построить её математическую модель и найти численные значения параметров этой модели. В качестве исходных данных для построения модели служат результаты эксперимента, который представляет собой совокупность нескольких измерений, выполненных по определённому плану. В простейшем случае план является описанием условий проведения измерений, то есть значения входных параметров (факторов) во время измерения.

В качестве примера систем, оценка параметров которых актуальна с практической точки зрения, могут служить различные технологические процессы. Для иллюстрации рассмотрим процесс фотолитографии.

Фотолитография представляет собой нанесение рисунка на поверхность фотографическим методом. Она состоит из следующих этапов: подготовка поверхности, нанесение фоточувствительной эмульсии (фоторезиста), сушка, установка трафарета или пластины с негативным рисунком, экспозиция (засвечивание) ультрафиолетовыми лучами, травление (проявление). Поскольку технологические тонкости фотолитографии в данном контексте не важны, в качестве основных факторов, влияющих на процесс литографии, будем считать толщину фоточувствительной эмульсии d(в микронах) и время экспозиции t(в секундах). Выходным параметром (откликом) процесса будем считать его разрешение R, то есть максимальное количество различимых линий, которые возможно провести на одном миллиметре поверхности. Эта величина определяется путём нанесения на поверхность специального тестового изображения.

Итак, технологический процесс фотолитографии описывается некоторой функцией вида

Построение модели технологического процесса позволяет выявить поведение отклика системы в зависимости от изменения факторов и тем самый найти пути для оптимизации технологии. Для данного конкретного случая — выбрать такую толщину эмульсии и время экспозиции, которые обеспечат наилучшее качество изображения.

В общем случае отклик системы описывается некоторой функцией переменных

Математическая модель системы получается в результате апроксимации этой функции какой-либо другой функцией, например линейной

,

где – искомые параметры модели.

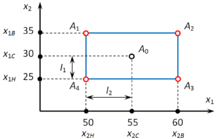
На рисунке в графическом виде представлен процесс построения линейной модели процесса фотолитографии, где – толщина плёнки фотоэмульсии, – время экспонирования, — разрешение, полученное в данных условиях. Функция нелинейна, однако в достаточной близости от точки её можно заменить касательной плоскостью . В показанной на рисунке области максимальная ошибка модели составляет .

Зная коэффициенты модели , можно с определённой точностью предсказывать значение функции (а значит и поведение системы) в окрестностях точки . В определении значений коэффициентов и состоит цель эксперимента.

Матрица эксперимента

Предположим, исходные параметры технологического процесса составляют: толщина плёнки 55 мкм, время экспозиции – 30 с, то есть

Возьмём верхние и нижние значения обоих факторов так, чтобы они располагались симметрично относительно текущего значения, например

Составим таблицу, в которой значения обоих факторов находятся во всех возможных сочетаниях и проведём измерения в этих точках (значения отклика даны условно):

Полагая, что линейная модель процесса имеет вид

,

на основании полученных результатов можно составить систему четырёх уравнений с двумя переменными. Ниже показана эта система, а также её сокращённая запись в виде матрицы. Матрицу данного вида назовём матрицей эксперимента.

В матрице эксперимента второй и третий столбцы представляют собой значения факторов, четвёртый столбец – значения отклика системы, а первый столбец содержит единицы, соответствующие единичным коэффициентам свободного члена модели . Будем считать этот столбец некоторым виртуальным фактором , который всегда принимает единичные значения.

Решение системы

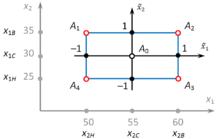
Чтобы облегчить решение системы, проведём нормировку факторов. Верхним значениям факторов присвоим нормированное значение +1, нижним значениям – нормированное значение –1, среднему значению – нормированное значение 0. В общем виде нормировка фактора выражается формулой

С учётом нормировки факторов система уравнений и матрица эксперимента примут следующий вид:

Поскольку сумма членов во втором и третьем столбце матрицы равны нулю, свободный член модели можно найти, сложив все четыре уравнения:

Чтобы найти какой-либо другой коэффициент модели, нужно изменить знаки в уравнениях таким образом, чтобы в соответствующем столбце оказались одни единицы, после чего сложить все четыре уравнения:

Таким образом, линейная модель технологического процесса в окрестностях точки (55, 30) имеет вид

В общем случае решение системы будет выглядеть как

Возврат к ненормированным факторам

Переход от нормированных к ненормированным факторам осуществляется обратным преобразованием

Чтобы найти параметры модели для ненормированных координат, подставим выражения для нормированных координат в уравнение модели:

Cравнивая последнее выражение с выражением для линейной модели в ненормированных координатах

,

получим выражения для параметров модели:

Для приведённого выше примера

Окончательно получаем модель в естественных координатах:

.

Полный факторный эксперимент

Матрица ПФЭ в общем виде

В общем виде матрица полного факторного эксперимента с n факторами имеет вид

Свойства матрицы ПФЭ

Матрица ПФЭ обладает следующими свойствами:

где – единичная матрица, ;

Вычисление коэффициентов линейной модели

Коэффициенты линейной модели в нормированных координатах вычисляются по формулам:

Коэффициенты линейной модели в естественных (ненормированных) координатах вычисляются по формулам:

Источник

Полный и дробный факторные эксперименты

Полным факторным экспериментом (ПФЭ) называется такой эксперимент, при реализации которого определяется значение параметра оптимизации при всех возможных сочетаниях уровней варьирования факторов. Если мы имеем дело с k факторами, каждый из которых устанавливается на q уровнях, то для осуществления полного факторного эксперимента необходимо произвести n=qk опытов.

Наибольшее распространение получили эксперименты, в которых факторы варьируют на 2-х уровнях, то есть n=2k, менее популярны эксперименты типа n=3k так как с ростом числа уровней факторов резко взрастает количество опытов.

Планирование, проведение и обработка результатов ПФЭ состоит из следующих обязательных этапов:

1) кодирование факторов;

2) составление план-матрицы эксперимента;

3) рандомизация опытов;

4) реализация планов эксперимента;

5) проверка воспроизводимости опытов;

6) проверка адекватности линейной модели;

7) оценка значимости коэффициентов уравнения.

Пример: Исследуем процесс повреждения семян в комбайне.

Цель эксперимента – определить зависимость повреждаемости семян подсолнечника от частоты вращения барабана и зазоров на входе между барабаном и подбарабаньем.

Предварительные исследования позволили установить технологически разумные пределы, в которых могут изменятся факторы:

1. Частота вращения n = 350…1350 об/мин;

2. Зазор между барабаном и подбарабаньем на входе

В таблице 1 представлены факторы в закодированном виде.

Нулевой уровень x₀ – выбирают обычно в центре интервала, в котором предполагается вести эксперимент.

Таблица 1 – Кодирование факторов

Интервал варьирования и уровни факторов	Частота вращения n, об/мин	Зазор δ, мм
Нулевой уровень хi=0	850	23
Интервал варьирования δi	400	4
Нижний уровень xi= –1	450	19
Верхний уровень xi= +1	1250	27
Кодовое обозначение	x1	x2

При выборе интервала варьирования необходимо учитывать, что при оптимизации процесса вначале целесообразно описать его линейным уравнением и поэтому интервал варьирования должен быть достаточно мал для получения линейных уравнений, и в то же время достаточно велик, чтобы не получить ошибочного вывода о незначимом влиянии какого либо из факторов.

Связь между кодовым и натуральным выражением фактора задаётся формулой:

(1)

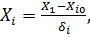
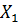
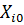
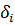
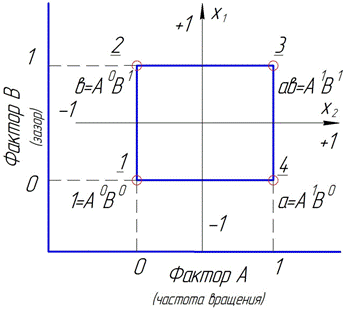
где – натуральное значение фактора;

– значение i-го фактора на нулевом уровне;

– интервал варьирования i-го фактора.

При постановке полного факторного эксперимента каждый уровень одного фактора сочетается с каждым уровнем другого. Такой план называют ортогональным планом первого порядка (рис. 1). Основным преимуществом такого плана является раздельная независимая оценка коэффициентов уравнения регрессии. Допустим, имеется двухфакторный эксперимент, в котором фактор А-(х₁) варьирует на двух уровнях: (-1) и (+1), столько же уровней имеет и фактор В-(х₂). В данном примере возможны 4 комбинации уровней, не считая повторностей каждой комбинации. Эти комбинации представлены графически вершинами квадрата, как показано на рисунке 1.

Рисунок 1 – Схема ортогонального плана первого порядка:

1, 2, 3, 4 – комбинации уровней.

Когда факторы А и В приняты на нижнем уровне, то их обозначают А₀В₀=(1) или, обозначая строчными латинскими буквами, пишут а₀b₀=(1). В этих случаях символ (1) есть отклик в испытании, где оба фактора на нижнем уровне.

Запись а₀b₁=b соответствует условию, что фактор В на верхнем уровне, а фактор А – на нижнем уровне. Запись а₁b₀=а показывает, что фактор А принят на верхнем, а фактор В – на нижнем уровне и а₁b₁=аb – оба фактора на верхних уровнях.

Комбинации условий эксперимента 22 можно выразить в виде таблицы, если обозначить нижний уровень фактора –1, а верхний +1. Такая таблица называется матрицей планирования эксперимента.

Матрицей планирования эксперимента называется таблица, содержащая условия проведения всех опытов в соответствии с выбранным планом.

Таблица 2 – Матрица планирования ПФЭ типа 2 2

Опыт	x1	x2
1	-1	-1
2	+1	-1
3	-1	+ 1
4	+1	+ 1

План эксперимента, приведенный в таблице 2, называют ортогональным планом первого порядка. Основное преимущество такого плана является раздельная (независимая) оценка коэффициентов регрессии.

Рандомизация опытов. На процесс дробления семян оказывают влияние не только факторы x₁ и x₂, но еще целый ряд факторов, которые могут быть вообще неизвестны исследователю.

Для того, чтобы внести элемент случайности влияния этих факторов на результат эксперимента, а это необходимо для обоснованного использования аппарата математической статистики, устанавливается случайный порядок постановки опытов во времени. Эта процедура называется рандомизацией. Для её осуществления используют таблицу случайных чисел или извлечения номеров из урны.

В рассматриваемом примере получили следующую последовательность проведения опытов: 2, 3, 1, 2, 4, 1, 3, 4. В этой последовательности каждое сочетание уровней (номера опытов) встречаются дважды.

Параллельные опыты предусматриваются для оценки воспроизводимости процесса и проведения статистических оценок.

Реализация плана эксперимента. Так как условились функцию отклика разложить в степенной ряд (Тейлора), то уравнение регрессии принимает вид (при k = 2):

Итак, при k=2 (x₁,x₂) количество опытов n=2k=22=4 опыта, то есть в данном случае 4 строки.

Число столбцов і примем равным числу членов в уравнении.

Таблица 3 – Полная план-матрица эксперимента

012345x₀x₁x₂x₁x₂x₁2x₂21+——+++2++——++3+—+—++4++++++

После построения плана-матрицы это количество уточняется.

1. В данном примере получилось лишь 4 различных столбца. Столбцы, соответствующие квадратам факторов, неотличимы от столбца x₀.

Это общий результат для планов ПФЭ 2k – они не позволяют определить коэффициенты при x_i 2 эти коэффициенты входят в коэффициент b₀. Поэтому ПФЭ 2k называют планом первого порядка и позволяют определить только коэффициенты при x₀ факторах x₁…x_k и взаимодействиях x_ij. Важно отметить, что при этом апроксимирующая поверхность пройдёт через все n точек, по которым она построена.

Такие планы-матрицы ещё называют ортогональными, а планирование называется ортогональным планированием.

Основное условие ортогональности – любое произведение суммы двух различных столбцов в матрице должно быть равно 0.

Определение коэффициентов уравнения регрессии при ортогональном планировании осуществляется по следующей формуле:

(2)

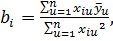
Таблица 4 – Стандартные планы

х₁х₂х₃х₄x₁x₂x₁x₃x₁x₄x₂x₃x₂x₄x₃x₄х₁₂₃х₁₂₄х₂₃₄х₁₃₄х₁₂₃₄1————+++2+——————3—+———++4++——+——5——+—+—+6+—+——+—7—++———8+++—+—9———+++10+——+——11—+—+—+12++—++—13——+++—14+—++—+15—+++——

При сопоставлении планов для различных значений k привлекает внимание то обстоятельство, что включение каждого нового фактора приводит к удвоению числа опытов в плане при k=6 число опытов n=64, 2 7 =128 и т.д.

Реализация таких планов становится трудной, дорогостоящей задачей и требующей больших затрат времени эффективность ПФЭ заметно снижается. Это обстоятельство привело к идее дробного факторного эксперимента (ДФЭ) или дробной реплики ПФЭ – ДФЭ.

Даже такая информация о процессе даёт возможность предположить, что некоторые из взаимодействующих факторов незначимы в той ограниченной части факторного пространства, в которой предполагается проведение эксперимента.

Если влияние некоторого взаимодействия признаётся пренебрежимо малым, то естественно, что коэффициент регрессии при таком взаимодействии не будет значимо отличаться от нуля. Это даёт возможность использовать соответствующий столбец расширенной матрицы для оценки влияния дополнительного фактора.

Опыт	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3
1	+	—	—	+	+	—	—	+
2	+	+	—	—	—	—	+	+
3	+	—	+	—	—	+	—	+
4	+	+	+	+	+	+	+	+

То есть строится план ПФЭ для меньшего числа факторов:

где р – количество взаимодействий в ПФЭ заменённое новыми факторами.

В полученной матрице имеются одинаковые столбцы, а это значит, что соответствующие коэффициенты неразличимы и можно судить лишь об их совместной величине. В данном случае b₀ неотличим от b₁₂₃, b₁ от b₂₃, b₂ от b₁₃ и b₃ от b₁₂. Получены смешанные оценки коэффициентов. Это не представляет опасности, если есть уверенность в том, что эффекты взаимодействия факторов равны нулю и тогда найдено то, что искали. Если же такой уверенности нет, то необходимо перейти к плану ПФЭ.

ДФЭ 2 3-1 – полуреплика.

2 5-2 – четверть реплика.

ДФЭ очень удобны при большом числе факторов (k > = 5).

Планы ПФЭ и ДФЭ позволяют найти коэффициенты в уравнении регрессии, если аппроксимируется поверхность хорошо описывается полиномом без квадратичных членов. Полученную модель можно использовать для прогнозирования значения отклика, и при любых значениях факторов, сходящихся внутри области определения факторов.

Для пояснения сказанного вернёмся к предыдущему примеру, то есть определим зависимость повреждаемости семян в комбайне от частоты вращения барабана и зазора между барабаном и подбарабаньем на входе при обмолоте подсолнечника.

Были приняты уровни факторов согласно таблице 1 и получены в результате проведения опытов значения функции отклика (таблица 5).

y

Опыт	х0	х1	х2	х12	у1	у2	у3	y
1	+	—	—	+	12	18	18	16	16
2	+	+	—	—	36	30	30	32	32
3	+	—	+	—	5	7	12	8	8
4	+	+	+	+	16	30	26	24	24

Вид уравнения регрессии необходимо получить следующий:

Определяем коэффициенты уравнения регрессии по известному соотношению (3):

таким образом, получен полином:

Решая уравнение относительно x₁ и x₂, получаем значение y, предсказанное уравнением, и видим, что получаемые значения равны экспериментальным. То есть, полученное уравнение адекватно описывает аппроксимируемую поверхность. Для проверки этого положения необходимо провести опыт в центре плана при х₁ и х₂ = 0.

Если полученный результат будет равен b₀ или иметь малые расхождения, то модель приемлема и на этом заканчивается первый этап исследований.

Если необходимо получить уравнение регрессии в натуральных переменных, необходимо раскодировать уравнение (6) с учётом соотношения (7.2):

В результате преобразований получим:

Проводится проверка воспроизводимости опытов, оценка значимости коэффициентов регрессии, а также проверка адекватности линейной модели:

а) проверка воспроизводимости опытов осуществляется по критерию Кохрена:

(8)

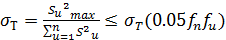
f_u = m–1 – число степеней свободы;

S_u 2 – дисперсия, характеризующая рассеяние результатов опытов;

Процесс воспроизводим, если выполняется неравенство по критерию Кохрена (8).

б) оценка значимости коэффициентов регрессии производится с помощью критерия Стьюдента:

где – табличное значение коэффициента Стьюдента;

S_y 2 – дисперсия воспроизводимости (ошибки опыта) определяется по формуле:

Полученные по расчету коэффициенты регрессии значимы, если выполняется условие по критерию Стьюдента (7.12).

в) проверка адекватности линейной модели выполняется с помощью критерия Фишера:

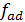
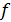
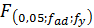
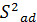
где — число степеней свободы дисперсии адекватности;

— число степеней свободы дисперсии воспроизводимости;

— табличное значение критерия Фишера при 5% уровне значимости;

– дисперсия адекватности.

где 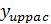– расчетное значение отклика в u-м опыте;

Модель адекватна, если выполняется условие по критерию Фишера.

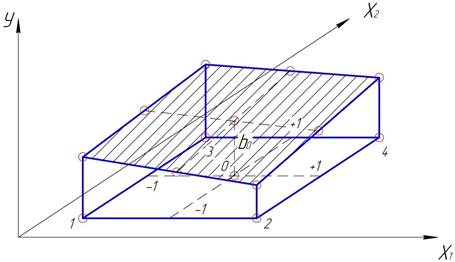
Рисунок 2 – Графическая интерпретация: гиперплоскость в

(k+1)-мерном факторном пространстве, когда k=2.

Как видно из рисунка 2, свободный член b₀ в линейном уравнении регрессии численно равен значению отклика при х₁=х₂=0.

В этом случае аппроксимация неполным квадратичным уравнением может оказаться неудовлетворительной. Это можно обнаружить, поставив дополнительный опыт в нулевой точке.

Итак, признак невозможности использования плана ПФЭ – нелинейность каких-либо сечений поверхности отклика.

Косвенный сигнал об этом несоответствии – расхождение между значениями и в нулевой точке плана.

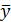
1.Что такое планирование эксперимента?

2.Какова цель планирования эксперимента?

3.Какие существуют основные методы планирования?

4.Что такое полный факторный эксперимент?

5.Как проводится кодирование факторов?

6.Как составить матрицу планирования?

7.Как проводится реализация плана эксперимента?

8.Как определяются коэффициенты регрессии при ортогональном планировании?

9.Что такое дробный факторный эксперимент?

10.Что такое уравнение регрессии?

11. Какие требования к факторам?

12. Какие требования к функции отклика?

Уважаемые обучающиеся, в процессе изучения дисциплины Вам необходимо выполнить расчетно-графическую работу «Планирование, проведение и обработка результатов многофакторного эксперимента».
Методические указания по которой представлены отдельным файлом.

Источник