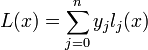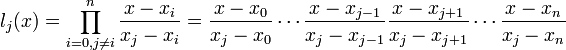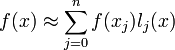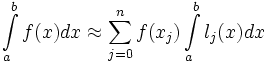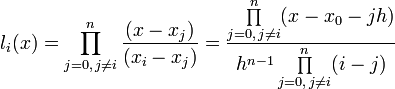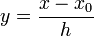Что такое полином лагранжа

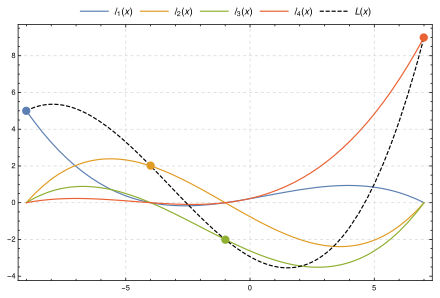
Полином Лагранжа

В простейшем случае ( n = 1 ) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Содержание

Определение

Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

Применения

Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.

Пусть для функции f(x) известны значения y_j = f(x_j) в некоторых точках. Тогда мы можем интерполировать эту функцию как

Для случая равномерного распределения по отрезку узлов интерполяции

В указанном случае можно выразить x_i через расстояние между узлами интерполяции h и начальную точку x₀ :

,

.

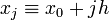
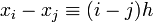
Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим

Теперь можно ввести замену переменной

Внешние ссылки

Полезное

Смотреть что такое «Полином Лагранжа» в других словарях:

ЛАГРАНЖА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — форма записи многочлена степени п(интерполяционного многочлена Лагранжа), интерполирующего заданную функцию f(х).в узлах х 0, x1. х п: В случае, когда значения х i являются равноотстоящими, т. е. с помощью обозначений (х x0)/h=t формула (1)… … Математическая энциклопедия

Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Полином Бернштейна — В вычислительной математике многочлены Бернштейна это алгебраические многочлены, представляющие собой линейную комбинацию базисных многочленов Бернштейна. [1] [2] Устойчивым алгоритмом вычисления многочленов в форме Бернштейна является алгоритм… … Википедия

Интерполирование — О функции, см.: Интерполянт. Интерполяция в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто … Википедия

Интерполяция (матем.) — О функции, см.: Интерполянт. Интерполяция в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто … Википедия

Интерполяция — О функции, см.: Интерполянт. Интерполяция, интерполирование в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и… … Википедия

Источник

Многочлен Лагранжа

В простейшем случае ( n = 1 ) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Содержание

Определение

Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

Применения

Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.

Пусть для функции f(x) известны значения y_j = f(x_j) в некоторых точках. Тогда мы можем интерполировать эту функцию как

Для случая равномерного распределения по отрезку узлов интерполяции

В указанном случае можно выразить x_i через расстояние между узлами интерполяции h и начальную точку x₀ :

,

.

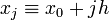
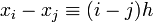
Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим

Теперь можно ввести замену переменной

Внешние ссылки

Полезное

Смотреть что такое «Многочлен Лагранжа» в других словарях:

Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Многочлен Бернштейна — В вычислительной математике многочлены Бернштейна это алгебраические многочлены, представляющие собой линейную комбинацию базисных многочленов Бернштейна. [1] [2] Устойчивым алгоритмом вычисления многочленов в форме Бернштейна является алгоритм… … Википедия

Многочлен Тейлора — Ряд Тейлора разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а также Ньютон. Ряды… … Википедия

Список объектов, названных в честь Лагранжа — Существует несколько математических и физических объектов, носящих имя французского математика XVIII века Луи Жозефа Лагранжа: Теоремы Теорема Лагранжа в математическом анализе см. формула конечных приращений Теорема Лагранжа (теория групп) … Википедия

Интерполяционный многочлен — Интерполяционный многочлен: Интерполяционный многочлен Лагранжа Интерполяционный многочлен Ньютона Интерполяция алгебраическими многочленами … Википедия

Источник

Интерполяционный многочлен в форме Лагранжа

1. Интерполяционная формула Лагранжа

В общем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде:

где ˗ степень полинома ;

˗ значение значения интерполирующей функции в точке ;

˗ базисные полиномы (множитель Лагранжа), которые определяются по формуле:

Так, например, интерполяционный многочлен в форме Лагранжа, проходящий через три заданных точки , будет записываться в следующем виде:

Многочлен в форме Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что при построении полинома степени n+1 полностью теряется информация о предыдущем полиноме степени n, т.е. с изменением числа узлов приходится все вычисление выполнить заново.

2. Погрешность интерполяционного полинома в форме Лагранжа

Рассмотрим функцию f ( x ), которая непрерывна и дифференцируема на рассматриваемом отрезке [a, b]. Интерполяционный полином L (x) в форме Лагранжа принимает в точках заданные значения функции . В остальных точках интерполяционный полином L (x) отличается от значения функции f ( x ) на величину остаточного члена, который определяет абсолютную погрешность интерполяционной формулы Лагранжа:

А бсолютную погрешность интерполяционной формулы Лагранжа определяют следующим образом:

где n ˗ степень полинома

Переменная представляет собой верхнюю границу значения модуля (n +1)-й производной функции f(x) на заданном интервале [a, b]

Погрешность интерполяции методом Лагранжа зависит от свойств функции f ( x ), а также от расположения узлов интерполяции и точки x. В случае если погрешность не достигает нужной точности, то нужно разбить отрезок на части и интерполировать каждую часть в отдельности – кусочная интерполяция.

Выбор узлов интерполяции

С помощью корректного выбора узлов можно минимизировать значение в оценке погрешности, тем самым повысить точность интерполяции. Данная задача может быть решена с помощью многочлена Чебышева:

В качестве узлов следует взять корни этого многочлена, то есть точки:

3. Методика вычисления полинома в форме Лагранжа

Алгоритм вычисления полинома в форме Лагранжа позволяет разделить задачи определения коэффициентов и вычисления значений полинома при различных значениях аргумента:

2. Выполняется вычисление полинома n-степени в форме Лагранжа по следующей формуле:

Алгоритм вычисления полинома в форме Лагранжа представлен на рисунке 1.

Методика вычисления полинома в форме Лагранжа

В качестве примера рассмотрим следующую практическую задачу. В рамках задачи известен набор шести значений, которые получены методом случайной выборки для различных моментов времени. Следует отметить, что данная выборка значений описывает функция на интервале [0, 10]. Необходимо построить многочлен в форме Лагранжа для представленного набора значений. С помощью интерполяционной формулы вычислить приближенное значение функции в точке , а также определить оценку погрешности результата вычислений.

Многочлен в форме Лагранжа, который строится на основании шести значений, представляет собой полином 5 степени. Результат построения полинома в форме Лагранжа показан в графическом виде.

С помощью найденного полинома можно определить значение функции в любой точке заданного интервала. Определение промежуточных значений величины по имеющемуся дискретному набору известных значений называется «интерполяцией». В соответствии с условиями задачи полином в форме Лагранжа в точке x =9,5 принимает следующее значение: L (9,5)= – 4,121. Из графика видно, что полученное значение не совпадает c о значением функции f ( x ) на величину абсолютной погрешности интерполяционной формулы Лагранжа.

Интерполяционный полином в форме Лагранжа часто оказывается удобным для проведения различных теоретических исследований в области вычислительной математики. Так, например, полином в форме Лагранжа используются для интерполяции, а также для численного интегрирования таблично-заданной функцией.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Источник

Лагранжа полином

В простейшем случае ( n = 1 ) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Содержание

Определение

Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

Применения

Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.

Пусть для функции f(x) известны значения y_j = f(x_j) в некоторых точках. Тогда мы можем интерполировать эту функцию как

Для случая равномерного распределения по отрезку узлов интерполяции

В указанном случае можно выразить x_i через расстояние между узлами интерполяции h и начальную точку x₀ :

,

.

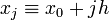
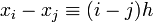
Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим

Теперь можно ввести замену переменной

Внешние ссылки

Полезное

Смотреть что такое «Лагранжа полином» в других словарях:

ЛАГРАНЖА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — форма записи многочлена степени п(интерполяционного многочлена Лагранжа), интерполирующего заданную функцию f(х).в узлах х 0, x1. х п: В случае, когда значения х i являются равноотстоящими, т. е. с помощью обозначений (х x0)/h=t формула (1)… … Математическая энциклопедия

Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Полином Бернштейна — В вычислительной математике многочлены Бернштейна это алгебраические многочлены, представляющие собой линейную комбинацию базисных многочленов Бернштейна. [1] [2] Устойчивым алгоритмом вычисления многочленов в форме Бернштейна является алгоритм… … Википедия

ИНТЕРПОЛИРОВАНИЕ — интерполяция, в простейшем, классическом смысле конструктивное восстановление (быть может, приближенное) функции определенного класса по известным ее значениям или значениям ее производных в данных точках. Пусть даны n+l точек сегмента D=[ а, b] … Математическая энциклопедия

ИНТЕРПОЛИРОВАНИЕ — в вычислительной математике способ приближенного или точного нахождения какой либо величины по известным отдельным значениям этой же или других величин, связанных с ней. На основе И. построен ряд приближенных методов решения математич. задач.… … Математическая энциклопедия

Интерполирование — О функции, см.: Интерполянт. Интерполяция в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто … Википедия

Источник

Полином Лагранжа

СОДЕРЖАНИЕ

Определение [ править ]

Учитывая набор из k + 1 точек данных

где нет двух одинаковых, интерполяционный полином в форме Лагранжа представляет собой линейную комбинацию Икс j <\ displaystyle x_ >

базисных многочленов Лагранжа

∀ ( j ≠ i ) : ℓ j ( x i ) = ∏ m ≠ j x i − x m x j − x m = ( x i − x 0 ) ( x j − x 0 ) ⋯ ( x i − x i ) ( x j − x i ) ⋯ ( x i − x k ) ( x j − x k ) = 0. <\displaystyle \forall ():\ell _(x_)=\prod _<\frac -x_>-x_>>=<\frac <(x_-x_<0>)><(x_-x_<0>)>>\cdots <\frac <(x_-x_)><(x_-x_)>>\cdots <\frac <(x_-x_)><(x_-x_)>>=0.>

Доказательство [ править ]

Искомая функция L ( x ) является полиномом от x наименьшей степени, который интерполирует данный набор данных; то есть, он принимает значение y _j в соответствующем x _j для всех точек данных j :

Также верно и то, что:

∑ j = 0 k ℓ j ( x ) = 1 ∀ x <\displaystyle \sum _^\ell _(x)=1\qquad \forall x>

поскольку он должен быть полиномом степени не выше k и проходить через все эти k + 1 точки данных:

Перспектива из линейной алгебры [ править ]

Кроме того, при большом порядке можно использовать быстрое преобразование Фурье для определения коэффициентов интерполированного полинома.

Примеры [ править ]

Пример 1 [ править ]

Мы хотим интерполировать ƒ ( x ) = x 2 в диапазоне 1 ≤ x ≤ 3, учитывая эти три точки:

x 0 = 1 f ( x 0 ) = 1 x 1 = 2 f ( x 1 ) = 4 x 2 = 3 f ( x 2 ) = 9. <\displaystyle <\beginx_<0>&=1&&&f(x_<0>)&=1\\x_<1>&=2&&&f(x_<1>)&=4\\x_<2>&=3&&&f(x_<2>)&=9.\end>>

Пример 2 [ править ]

Мы хотим интерполировать ƒ ( x ) = x 3 в диапазоне 1 ≤ x ≤ 4, учитывая эти четыре точки:

L ( x ) = 1 ⋅ x − 2 1 − 2 ⋅ x − 3 1 − 3 ⋅ x − 4 1 − 4 + 8 ⋅ x − 1 2 − 1 ⋅ x − 3 2 − 3 ⋅ x − 4 2 − 4 + 27 ⋅ x − 1 3 − 1 ⋅ x − 2 3 − 2 ⋅ x − 4 3 − 4 + 64 ⋅ x − 1 4 − 1 ⋅ x − 2 4 − 2 ⋅ x − 3 4 − 3 = x 3 <\displaystyle <\beginL(x)&=<1>\cdot \cdot \cdot +<8>\cdot \cdot \cdot +<27>\cdot \cdot \cdot +<64>\cdot \cdot \cdot \\[8pt]&=x^<3>\end>>

Заметки [ править ]

Барицентрическая форма [ править ]

мы можем переписать базисные полиномы Лагранжа как

ℓ j ( x ) = ℓ ( x ) ℓ ′ ( x j ) ( x − x j ) <\displaystyle \ell _(x)=<\frac <\ell (x)><\ell '(x_)(x-x_)>>>

или, определяя барицентрические веса [4]

мы можем просто написать

ℓ j ( x ) = ℓ ( x ) w j x − x j <\displaystyle \ell _(x)=\ell (x)<\frac >>>>

которую обычно называют первой формой формулы барицентрической интерполяции.

Преимущество этого представления состоит в том, что полином интерполяции теперь может быть оценен как

L ( x ) = ℓ ( x ) ∑ j = 0 k w j x − x j y j <\displaystyle L(x)=\ell (x)\sum _^<\frac >>>y_>

L ( x ) = ∑ j = 0 k w j x − x j y j ∑ j = 0 k w j x − x j <\displaystyle L(x)=<\frac <\sum _^<\frac >>>y_><\sum _^<\frac >>>>>>

Остаток в формуле интерполяции Лагранжа [ править ]

Остаток можно связать как

Вывод [6] [ править ]

Уравнение можно переписать как

Производные [ править ]

L ( d ) ( x ) := ∑ j = 0 k y j ℓ j ( d ) ( x ) <\displaystyle L^<(d)>(x):=\sum _^y_\ell _^<(d)>(x)> .

Для первой производной коэффициенты имеют вид

а для второй производной

С помощью рекурсии можно вычислить формулы для высших производных.

Конечные поля [ править ]

Источник