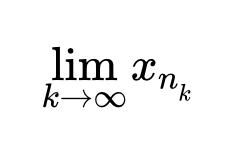Что такое подпоследовательность последовательности

Подпоследовательности. Частичные пределы.

Подпоследовательность.

Пусть задана последовательность \(\\>\). Рассмотрим строго возрастающую последовательность \(\\) натуральных чисел, то есть такую, что
$$
n_ <1>Теорема.

Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

\(\circ\) Пусть \(\\>\) — ограниченная последовательность, тогда все члены последовательности принадлежат некоторому отрезку, то есть
$$
\exists a, \ b:\forall n\in\mathbb\rightarrow x_\in\Delta=[a, \ b].\label
$$

Разобьем отрезок \(\Delta=[a, \ b]\) пополам точкой d. Тогда по крайней мере один из отрезков \([a, \ d], \ [d, \ b]\) содержит бесконечное число членов последовательности \(\\>\). Если оба отрезка обладают этим свойством, возьмем, например, правый отрезок (и будем так поступать в дальнейшем). Выбранный отрезок, содержащий бесконечное число членов данной последовательности, обозначим \(\Delta_1=[a_<1>, \ b_<1>]\), его длина равна
$$
b_<1>-a_<1>=\frac<2>.\nonumber
$$

Разделив отрезок \(\Delta_<1>\) пополам, выберем указанным выше способом из двух получившихся отрезков отрезок \(\Delta_<2>=[a_<2>,b_<2>]\), содержащий бесконечное число членов последовательности \(\\>\).

Продолжая эти рассуждения, получим последовательность \(\<\Delta_n=[a_n, \ b_n]\>\) отрезков таких, что:

Следовательно, \(\Delta_n\) — стягивающаяся последовательность отрезков. По теореме Кантора существует единственная точка c, принадлежащая всем отрезкам, то есть
$$
\exists c:\forall k\in\mathbb\rightarrow c\in\Delta_.\label
$$

Покажем, что найдется подпоследовательность \(\>\>\) последовательности \(\\>\) такая, что
$$
\lim_x_>=c.\label
$$

Так как отрезок \(\Delta_<1>\) содержит бесконечное число членов последовательности \(\\), то
$$
\exists n_<1>\in\mathbb:x_>\in\Delta_<1>.\nonumber
$$

Отрезок \(\Delta_<2>\) также содержит бесконечное число членов данной последовательности, и поэтому
$$
\exists n_2>n_1: x_\in\Delta_2.\nonumber
$$
Вообще, можно записать, что
$$
\forall k\in\mathbb\quad\exists n_k: \ x_\in\Delta_k, \ где \ n_1 Замечание.

Теорему Больцано-Вейерштрасса можно сформулировать так: любая ограниченная последовательность имеет хотя бы один частичный предел.

Источник

Как понимать подпоследовательность?

Это любая последовательность, состоящая из подмножества элементов последовательности, сохраняющая их порядок.

Как придумаете, так и будет работать. Вектором или массивом логических значений можно задать, какие элементы последовательности выбираются для участия в подпоследовательности. Или множеством индексов элементов. Или возрастающим массивом/вектором индексов.

Последовательность:
│10 20 30 40 50│
Трафарет:
│ ██ ██│
Накладываем трафарет, получаем подпоследовательность:
│10 ██ 30 40 ██│
Или, схлопнув вычеркнутое:
│10 30 40│

Трафарет, задающий подпоследовательность, можно задать как множество. Множество можно задать массивом логических значений:
[true, false, true, true, false]
Или множеством индексов
[2, 0, 3]
Если это множество упорядочить, получится массив индексов
[0, 2, 3]
Первый элемент подпоследовательности имеет индекс 0, а в последовательности под этим индексом находится 10. Второй элемент подпоследовательности имеет индекс 2, и по этому индексу 30. Аналогично 40.

Дана последовательность пар.
В этой последовательности могут встречаться непрерывные подпоследовательности.

Александр, В последовательности длины n можно разглядеть O(n²) непрерывных подпоследовательностей. Предложение выглядит так, будто обрывается на середине, а дальше должно было быть написано какое-нибудь интересное свойство этих подпоследовательностей.

Наиболее логичное предположение о том, что же это за свойство, — это то, что второй элемент пары равен первому элементу следующей за ним пары, и так по цепочке.

OCTAGRAM, Полный текст такой.
Дана последовательность пар (int Х : int Y). Пары упорядочены по значениям Х.

В этой последовательности могут встречаться непрерывные подпоследовательности, состоящие из идентичных отсчетов. Идентичные отсчеты имеют одинаковые значения Y.

Александр, а, ну тогда всё ясно. Тогда проще всего задать непрерывную подпоследовательность краями, либо началом и длиной.

Могут встречаться — значит, они не заданы, а их можно, наоборот, найти. И, скорее всего, интерес представляют только подпоследовательности наибольшей длины.

Делается проход от начала до конца, и пока Y сохраняется, увеличивать длину, а как поменялся, так зарегистрировать подпоследовательность и сбросить длину. И после прохода по всей последовательности регистрируется подпоследовательность, которая была в конце.

А, может, то обстоятельство, что что-то встречается, дано просто для справки, то есть, используется косвенно.

Источник

Математический анализ
Записки лекций

Илья Щуров (НИУ ВШЭ)

9 Подпоследовательности, предельные точки и теорема Больцано — Вейерштрасса

9.1 Подпоследовательности и предельные точки

9.1.1 Подпоследовательности

Доказательство первых двух пунктов этого утверждения простое и я советую его провести самостоятельно. Третий пункт вынесен в качестве задачи на семинары. Обратное неверно: если подпоследовательность обладает каким-нибудь из этих свойств (скажем, ограничена), это ничего не говорит про аналогичное свойство исходной последовательности (приведите примеры).

Неверный ответ. Попробуйте доказать 🙂

9.1.2 Предельные точки

При решении некоторых задач удобным оказывается другое определение предельной точки.

Сравните это определение с определением предела — в чём ключевое различие?

Есть ли последовательности, не имеющие предельных точек? Тут легко привести пример — скажем, последовательность a n = n обладает таким свойством: она посещает каждое натуральное число ровно один раз, а потом уходит от него на расстояние как минимум 1.

Заметим, что последовательсноть a n = n неограничена. Бывают ли ограниченные последовательности без предельных точек? Прежде, чем читать дальше, попробуйте придумать такую.

9.2 Теорема Больцано — Вейерштрасса

Для доказательства этой теоремы нам понадобится вспомогательная лемма, которая представляет и самостоятельный интерес — она пригодится нам ещё несколько раз.

9.2.1 Лемма о вложенных отрезках

Потребуем также, чтобы длины отрезков стремились к нулю:

Неверный ответ. Какие же это?

9.2.2 Деление отрезка пополам

Источник

Подпоследовательности и частичные пределы последовательностей

Определение подпоследовательности

Свойства подпоследовательностей

Свойство 3 является следствием свойств 1 и 2.

Частичный предел последовательности

Произвольная последовательность может иметь конечное или бесконечное число частичных пределов ⇑.

5. Свойство частичного предела последовательности
Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.
Доказательство ⇓

Верхний и нижний частичные пределы

Рассмотрим множество частичных пределов последовательности. Эта теорема утверждает, что верхняя и нижняя грани этого множества являются ее элементами. То есть множество частичных пределов последовательности замкнуто, оно содержит свою границу. Для произвольного множества это может не выполняться. Например, для открытого интервала не существует наибольшего и наименьшего элемента, поскольку и верхняя грань b и нижняя a не принадлежит этому множеству.

Если последовательность не ограничена сверху, то ее верхний частичный предел равен плюс бесконечности:
.
Соответственно, если последовательность не ограничена снизу, то
.

Если последовательность ограничена, то ее верхний и нижний частичные пределы конечны.

8. Теорема о неравенстве между верхним и нижним частичными пределами
Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.
Доказательство ⇓

9. Связь верхних и нижних пределов между последовательностями n> и <–x_n>.
Имеет место очевидное равенство:
.

10. Свойства верхних и нижних пределов суммы последовательностей
Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.
Доказательство ⇓

11. Свойство верхних пределов произведения последовательностей
Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.
Доказательство ⇓

Применяя равенство
,
можно получить другие подобные соотношения.

Доказательство свойств и теорем

Далее перечислены определения и свойства, которые мы будем использовать при доказательстве свойств подпоследовательностей.

1. Свойство подпоследовательностей сходящейся последовательности

2. Свойство последовательности, все подпоследовательности которой сходятся к одному числу

5. Свойство частичного предела последовательности

Все свойства ⇑ Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.

Возьмем произвольную окрестность точки a : ⇑. В качестве первого члена подпоследовательности возьмем любой член последовательности, принадлежащий этой окрестности.

6. Теорема о существовании верхнего и нижнего частичных пределов

В этом случае точка является верхним частичным пределом последовательности.

Пусть последовательность ограничена сверху и при этом любой отрезок содержит только конечное число членов последовательности.

Поскольку мы выбирали самые правые отрезки с бесконечным числом членов, то точка c является верхним частичным пределом последовательности.

7. Свойство верхнего и нижнего частичных пределов

8. Теорема о неравенстве между верхним и нижним частичными пределами

Все свойства ⇑ Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.

10. Свойства верхних и нижних пределов суммы последовательностей

Все свойства ⇑ Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.

Докажем второе неравенство:
.
Умножим первое неравенство на – 1 :
.
Применим свойство 8 ⇑:
.

11. Свойство верхних пределов произведения последовательностей

Все свойства ⇑ Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.

Из (10.1) и (10.2) следует, что
.
Свойство доказано.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Задача о наибольшей общей подпоследовательности

Содержание

Наивное решение [ править ]

Переберем все различные подпоследовательности обеих строк и сравним их. Тогда искомая [math]LCS[/math] гарантированно найдётся, однако время работы алгоритма будет экспоненциально зависеть от длины исходных последовательностей.

Динамическое программирование [ править ]

Для решения данной задачи используем Принцип оптимальности на префиксе.

Доказательство оптимальности [ править ]

Решение [ править ]

Обозначим как [math] lcs[i][j] [/math] [math]LCS[/math] префиксов данных последовательностей, заканчивающихся в элементах с номерами [math] i [/math] и [math] j [/math] соответственно. Получается следующее рекуррентное соотношение:

Построение подпоследовательности [ править ]

Псевдокод [ править ]

Оптимизация для вычисления только длины [math]LCS[/math] [ править ]

Длина кратчайшей общей суперпоследовательности [ править ]

Решение для случая k строк [ править ]

Найдем решение для 3 строк.

Наивное решение подсчёта [math]LCS[/math] нескольких строк при помощи последовательного нахождения [math]LCS[/math] двух строк и уменьшением набора строк на единицу, не срабатывает. Это доказывается следующим контрпримером. Даны три последовательности:

[math]X = \left \langle A, B, C, D, E\right \rangle [/math]

[math]Y = \left \langle D, E, A, B, C\right \rangle [/math]

[math]Z = \left \langle D, E, F, G, H\right \rangle [/math]

Подсчитаем [math]V = LCS(X,Y) = \left \langle A, B, C \right \rangle[/math]

Это неверно, так как [math]LCS(X,Y,Z) = \left \langle D, E \right \rangle[/math]

Доказательство:[math]\triangleright[/math]Доказательство аналогично доказательству для двух последовательностей.[math]\triangleleft[/math]

Решение [ править ]

Алгоритм Хиршберга [ править ]

Алгоритм [ править ]

Псевдокод [ править ]

Доказательство корректности [ править ]

Асимптотика [ править ]

Источник