Что такое плоский многоугольник
Многоугольник
Многоуго́льник — это геометрическая фигура, обычно определяется как замкнутая ломаная,имеющая больше одного угла.
Существуют три различных варианта определения многоугольника:
В любом случае, вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Содержание
Связанные определения
Виды многоугольников
Свойства
Вариации и обобщения
Планигон
Полезное
Смотреть что такое «Многоугольник» в других словарях:
многоугольник — многоугольник … Орфографический словарь-справочник
МНОГОУГОЛЬНИК — (на плоскости) геометрическая фигура, ограниченная замкнутой ломаной линией, звенья которой называются сторонами многоугольника, а их концы вершинами многоугольника. По числу вершин различают треугольники, четырехугольники и т. д. Многоугольник… … Большой Энциклопедический словарь
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, плоская геометрическая фигура с тремя или более сторонами, пересекающимися в трех или более точках (вершинах). Они называются в соответствии с числом сторон или вершин: ТРЕУГОЛЬНИК (трехсторонний); ЧЕТЫРЕХУГОЛЬНИК… … Научно-технический энциклопедический словарь
многоугольник — полигон Словарь русских синонимов. многоугольник сущ., кол во синонимов: 12 • восьмиугольник (3) • … Словарь синонимов
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, многоугольника, муж. (мат.). Плоская фигура, ограниченная тремя, четырьмя и т.д. прямыми линиями. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, а, муж. В математике: геометрическая фигура, ограниченная замкнутой ломаной линией. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Многоугольник — Многоугольник. В элементарной геометрии М. называется фигура,ограниченная прямыми линиями, называемыми сторонами. Точки, в которыхстороны пересекаются, называются вершинами. Число вершин равняется числусторон. Смотря по этому числу, М. называются … Энциклопедия Брокгауза и Ефрона
многоугольник — (напр. сил) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN polygon … Справочник технического переводчика
многоугольник — а; м. Геометрическая фигура, ограниченная ломаной линией, звенья которой образуют более четырёх углов. Правильный м. Сторона многоугольника. * * * многоугольник (на плоскости), геометрическая фигура, ограниченная замкнутой ломаной линией, звенья… … Энциклопедический словарь
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
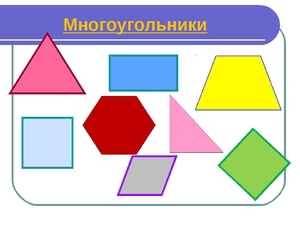
Виды многоугольников
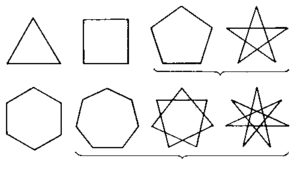
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
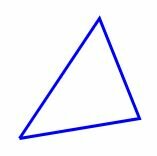 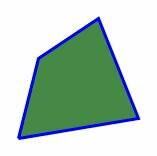 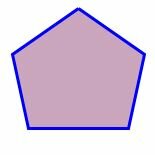  |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
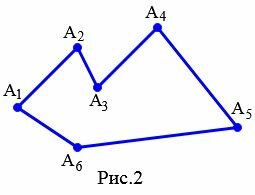 |
На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
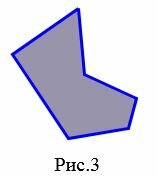 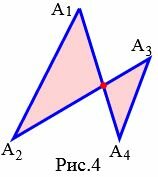 |
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
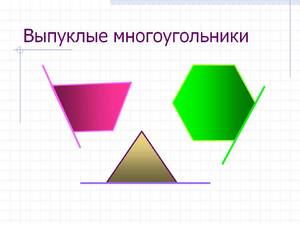
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
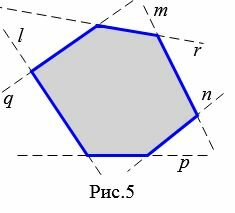 |
На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
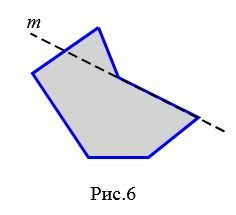 |
На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
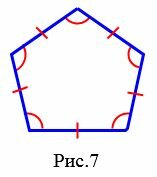 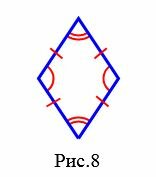 |
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
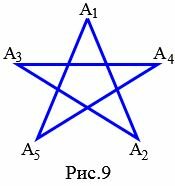 |
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
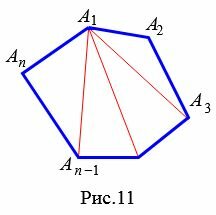 |
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
Геометрическая фигура многоугольник
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
Виды фигур
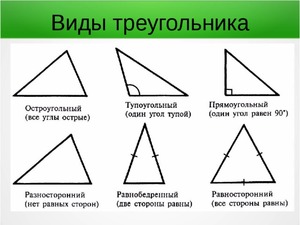
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
Кроме того, принято различать следующие треугольники:
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
» width=»560″ height=»314″ allowfullscreen=»allowfullscreen»>Многоугольники (ЕГЭ 2022)
Никогда не было интересно, почему в треугольнике 180 градусов?
А в других фигурах сколько? Да постой, положи транспортир!
Сейчас ты узнаешь много нового о такой, казалось бы, простой теме, как многоугольники.
Многоугольники — коротко о главном
Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,
Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.
Например: многоугольник c \( \displaystyle 4\) сторонами называют четырехугольником, многоугольник с \( \displaystyle 6\) сторонами — шестиугольником и так далее по аналогии.
Выпуклый многоугольник – многоугольник лежащий по одну сторону от любой прямой, соединяющей его соседние вершины.
Сумма внутренних углов выпуклого n-угольника равна \( \displaystyle 180<>^\circ \cdot (n-2)\) или \( \displaystyle <<\alpha >_<1>>+<<\alpha >_<2>>+\text< >…
Правильный выпуклый многоугольник – многоугольник все стороны и внутренние углы которого равны.
Внутренний угол правильного \( \displaystyle n\)-угольника равен \( \displaystyle \alpha =\frac
\cdot 180<>^\circ \).
Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.
Центры вписанной в правильный многоугольник окружности и окружности, описанной около него, совпадают.
Если многоугольник такой, что в него можно вписать окружность, то его площадь выражается формулой: \( \displaystyle S=pr\), где \( \displaystyle p=\frac<<_<1>><_<2>>+<_<2>><_<3>>+…+<_
><_<1>>><2>\).
Многоугольник — подробнее
Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,
При этом смежные стороны (имеющие общую вершину) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (то есть не должны пересекаться).
Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.
Произвольные многоугольники
Давай-ка нарисуем, какие бывают многоугольники.
А теперь вопрос: какой из этих многоугольников выпадает из ряда?
Посмотри внимательно на второй многоугольник — он отличается от всех остальных. Чем же?
Это не выпуклый многоугольник. Это, конечно, математическое название, но с человеческой интуицией не расходится.
Ну вот, а мы будем рассматривать только выпуклые многоугольники, то есть такие, как 1),3),4) и т.п.
Итак, основной факт:
В любом многоугольнике сумма внутренних углов равна \( \displaystyle 180^o(n-2)\), где буква «\( \displaystyle n\)» означает число углов многоугольника.
Давай сразу к примерам:
Четырехугольник
Пятиугольник
Шестиугольник
Ах да, про треугольник забыли.
Треугольник
Сумма углов многоугольника. Доказательство.
А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника \( \displaystyle 180^\circ(n-2)\).
Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.
Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.
Итак, давай разделим многоугольник на треугольники.
Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:
Всего вершин: \( \displaystyle n\)
Из вершины \( \displaystyle B\) можем провести диагонали во все вершины, кроме:
Значит всего диагоналей \( \displaystyle (n-3)\). А на сколько треугольников распался наш многоугольник?
Представь себе: на \( \displaystyle n-2\). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.
Итак, у нас ровно \( \displaystyle n-2\) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.
Чему равна сумма углов треугольника? Помнишь? Конечно \( \displaystyle 180<>^\circ \).
Ну вот, \( \displaystyle n-2\) треугольника, в каждом по \( \displaystyle 180<>^\circ \), значит:
Сумма углов многоугольника равна \( \displaystyle 180<>^\circ \)\( \displaystyle (n-2)\)
Что же из этого может оказаться полезным? Два момента:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Правильные многоугольники
Многоугольник называется правильным, если все его углы и все его стороны равны.
Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.
Первый вопрос:
А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?
Давай посмотрим на примере.
Пусть есть, скажем, правильный восьмиугольник:
Сумма всех его углов равна \( \displaystyle 180<>^\circ \left( 8-2 \right)=1080<>^\circ \).
А сколько всего углов? Восемь конечно, и они все одинаковые.
Значит любой угол, скажем \( \displaystyle \angle A\) можно найти:
\( \displaystyle \angle A=\frac<1080<>^\circ ><8>=135<>^\circ \).
Что мы еще должны знать?
Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.
При этом центры этих окружностей совпадают.
Смотри, как это выглядит!
И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.
Давай опять на примере восьмиугольника.
Посмотри на \( \displaystyle \Delta OKG\). В нем \( \displaystyle OK=r,OG=R.\)
Значит, \( \displaystyle \frac
Чему же равен в нашем случае \( \displaystyle \angle x\)?
Ровно половине \( \displaystyle \angle G\), представь себе!
Значит \( \displaystyle \angle x=\frac<135<>^\circ ><2>=67,5<>^\circ \).
Смешно? Но так и есть! Поэтому для восьмиугольника \( \displaystyle \frac
Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки \( \displaystyle O\)?
И тот же ответ: конечно можно!
Опять рассмотрим наш восьмиугольник. Вот мы хотим найти \( \displaystyle \angle \alpha\) (то есть \( \displaystyle \angle HOG\)).
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
И так можно все находить не только для восьмиугольника, но и для любого правильного многоугольника.
Бонус. Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 6. Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.
Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
А теперь твоя очередь!
Теперь ты знаешь все о многоугольниках!
Особенно эти знания пригодятся тебе, когда будешь решать задачи про окружности. Задачи олимпиадного уровня. Да и просто так знать полезно 🙂
А сейчас мы хотим услышать тебя. Понравилась ли тебе статья? Ты во всем разобрался?
Кстати, пытался строить многоугольники циркулем?
Напиши в комментариях ниже!
И задай любые вопросы, если они возникли! Мы непременно ответим!
Добавить комментарий Отменить ответ
3 комментария
Як разбить чатырох угольник так, чтоб палучился трохвугольник и чатырохвугольник
Даша, например, можно провести отрезок из вершины в середину противоположной стороны.
Некоторые комментарии прошлых лет к этой статье:
Сергей
19 февраля 2018
Просто огромное спасибо. Хоть что-то начал понимать.
Александр (админ)
19 февраля 2018
Просто огромное пожалуйста. 🙂 Очень приятно слышать от вас такие слова.
Вероника
18 марта 2020
Спасибо большое, а то на карантине приходится самим разбирать темы!
Александр (админ)
18 марта 2020
Отлично, Вероника! Круто, что ты сама пытаешься разобраться с математикой! Этот навык ой как пригодится в будущем. Я всегда говорю: «В жизни репетитора и учителя рядом не будет». И я рад, что наш скромный сайт в этом помогает. Удачи на экзаменах! Все будет хорошо!
Сима
01 июля 2020
Блин, действительно очень круто изложили. А главное- понятно и просто. Начала подготовку к егэ, в следующем году сдавать. Очень помогли разобраться с этой темой! Спасибо)
Александр (админ)
01 июля 2020
Блин, Сима, до чертиков приятно слышать такие слова! 🙂 Если начала подготовку к ЕГЭ, то будь на связи, мы сейчас делаем крутейший курс подготовки к ЕГЭ, где вот так вот просто все будет объяснять Алексей Шевчук.