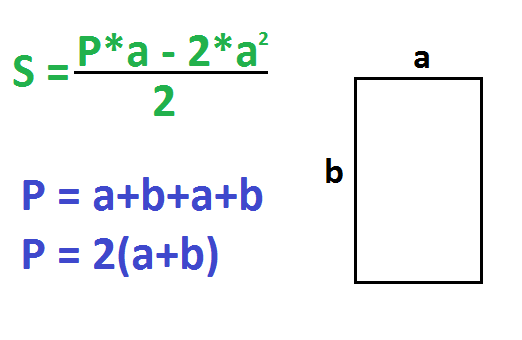Что такое площадь прямоугольника 2 класс правило
Как найти площадь прямоугольника – 9 способов с формулами и примерами
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
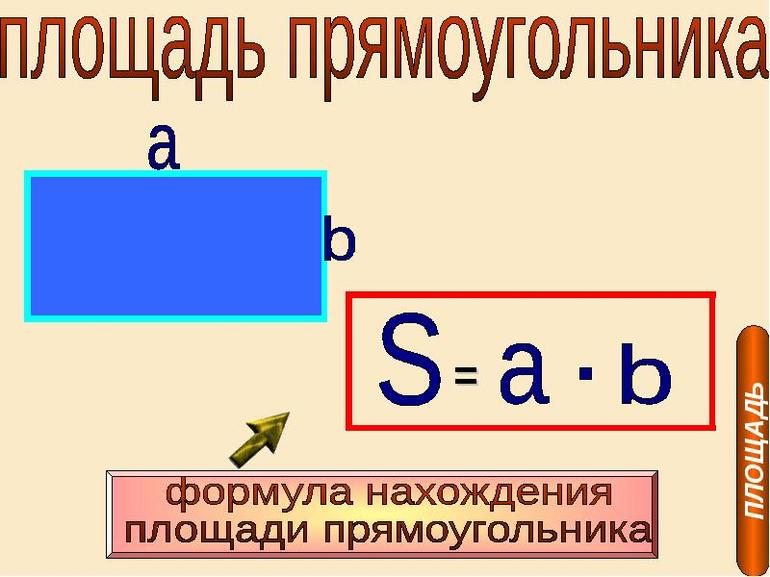
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
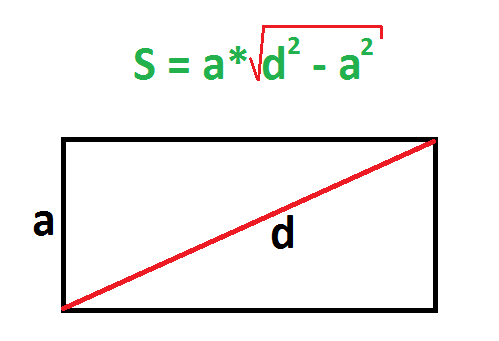
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
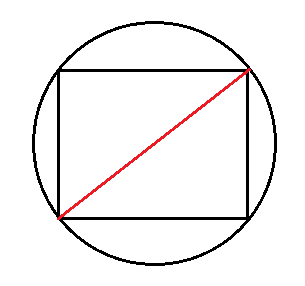
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
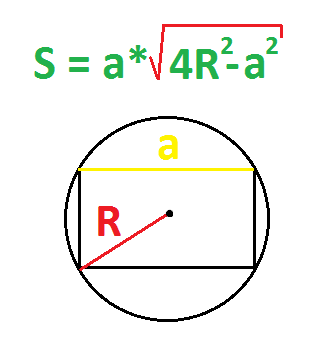
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
По стороне и периметру – 2 способ
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
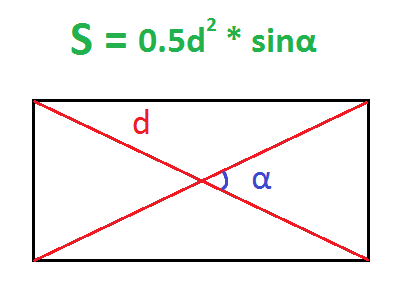
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
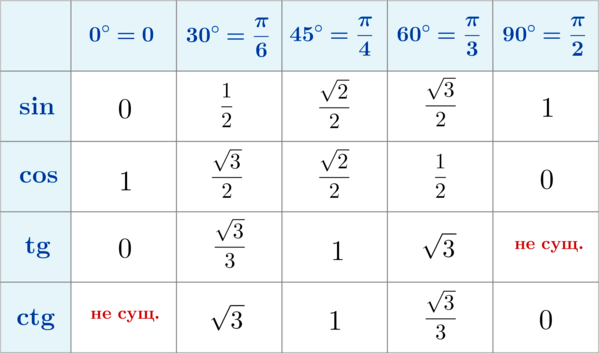
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
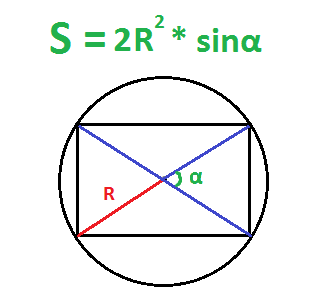
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
По радиусу описанной окружности и углу между диагоналями – второй способ
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
Урок математики во 2-м классе по теме: «Площадь прямоугольника»
ХОД УРОКА
1. Самоопределение к деятельности
а) – Проследите глазками по моим командам. “Соберите” буквы – расшифруйте мое пожелание.
– Улыбнитесь и пожелайте удачи друг другу, ведь “С маленькой удачи начинается большой успех!”
б) – Какие две большие темы мы изучили на предыдущих уроках? (Единицы площади. Умножение.)
– Чему мы учились в теме: “Единицы площади”? (Измерять площадь фигур с помощью мерок)
– А что такое умножение? (Сложение одинаковых слагаемых)
– Сегодня эти знания нам очень пригодятся.
2. Актуализация знаний и фиксация затруднения в деятельности
а) – На какие группы можно разделить данные именованные числа:
(– однозначные, двузначные и трехзначные числа;
– круглые и некруглые числа;
– с нулем и без нуля;
– единицы длины и единицы площади)
– Назовите результаты измерения площади.
б) – Замените сумму произведением:
– Как называются компоненты при умножении?
– Что обозначает первый множитель?
– Что обозначает второй множитель?
– Что интересного заметили в произведениях? (Первый множитель уменьшается на 10)
в) – Найдите лишнее выражение в данной записи. Объясните свой выбор.
a·b (буквенное, остальные – числовые)
– Прочитайте по-разному второе выражение.
– Найдите его значение. (12)
г) – работа в тетради
Решим задачи. Запишите только выражение.
1) В одной коробке 6 карандашей. Сколько карандашей в 4 таких коробках? (6•4)
2) В одной вазе 9 цветов. Сколько цветов в 5 таких вазах? (9•5)
3) Одна сторона прямоугольника равна 4см, а вторая – 3см. Чему равна площадь прямоугольника?
(Дети решают задачи самостоятельно, затем – проверка)
3. Постановка учебной задачи
– Какое задание вызвало наибольшее затруднение?
– Почему вы не смогли решить эту задачу? (Не знаем, как найти площадь)
– Что же мы должны узнать на уроке? Какова цель урока? (Узнать, как вычислять площадь прямоугольника)
– Сформулируйте тему урока. (Площадь прямоугольника)
4. “Открытие” нового знания
– Как вы предлагаете решить задачу?
– Как мы находили площадь фигур на прошлых уроках? (Измеряли с помощью мерок)
– Какую мерку мы выбирали? (см 2 )
– Можем мы воспользоваться этим способом для решения задачи? (Да)
– Будем работать в группах. (Каждой группе из 4–5 человек дается карточка:
Длины сторон прямоугольника 4 см и 3 см. Чему равна его площадь?)
– На сколько строчек (столбиков) разбит прямоугольник?
– Сколько см 2 умещается в каждой из них?
– Как же узнать, сколько всего кв. см помещается в прямоугольнике, т.е. какова площадь этого прямоугольника? (3•4=12(см 2 ) или 4•3=12(см 2 ))
– Проверим работу в группах.(Вызывается к доске капитан первой команды).
– Кто решал таким же способом? Сравните. Все ли верно?
– А кто решал по-другому? Объясните.
– Каким же действием узнавали площадь прямоугольника? (Умножением)
– Какие числа перемножали? (3 и 4)
– Что выражают эти числа? (длины сторон; длину и ширину)
– Сделайте вывод, как же найти площадь прямоугольника? (Чтобы найти площадь прямоугольника, надо умножить длины сторон)
– Как можно сказать по-другому, чему равна площадь прямоугольника? (Площадь прямоугольника равна произведению длин сторон)
– Как это правило можно записать в виде буквенного равенства? (S = a•b)
– Сравните ваш вывод с правилом в учебнике, с.73. Согласны с нашим выводом авторы учебника?
– Это равенство в математике называют формулой. Ее можно использовать для вычисления площади любого прямоугольника.
– Как удобнее узнавать площадь прямоугольника: с помощью мерок или пользуясь формулой? Почему? (С помощью формулы быстрее; если длины сторон выражены в метрах, то не сможем начертить)
5. Первичное закрепление во внешней речи
Работа по учебнику с.73 №2
а) с комментированием хором
(Длина прямоугольника 4см. Пишу a=4 см. Ширина прямоугольника 2 см. Пишу b=2 см. площадь прямоугольника равна произведению длин его сторон. Пишу S= 4•2=8 (см 2 )
б) с комментированием сильный ученик с.74 №3(а) – в парах, проговаривая друг другу
(Одна пара работает у доски)
– Какие были ошибки? Почему?
– Над чем стоит поработать?
Дети встают в 2 колонны и кладут друг другу руки на плечи. По сигналу учителя выполняют следующие команды:
– присесть
– встать
– встать на цыпочки
– наклониться влево
– наклониться вправо
– шаг вперед
– наклон вперед
– прогнуться назад
– прыгнуть
– постоять на правой ноге, согнув левую в колене
– поворот влево
– согнуть правую ногу
– “волна”
6. Самостоятельная работа с самопроверкой
– Кто решил, встаньте.
(При проверке записи открываются по частям)
2•3 – У кого нет ошибок в записи выражения, поднимите правую руку.
=6 – Если вычислили верно, поднимите левую руку.
(м 2 ) – Если верно записали единицы площади, хлопните.
– У кого были ошибки? Какие? Исправьте. Очень хорошо, что вы их увидели. Значит, нам есть над чем работать на следующем уроке.
7. Включение в систему знаний
Стороны одного прямоугольника 12 см и 25 см, а другого – 16 см и 28 см. Площадь какого прямоугольника больше?
(S первого прямоугольника 12•25
S второго прямоугольника 16•28
S второго прямоугольника больше, чем S первого прямоугольника, т.к. чем больше множители, тем больше произведение)
8. Рефлексия деятельности
– Что нового узнали на уроке?
– Чему же равна площадь прямоугольника?
– Кто доволен своей работой?
– Кого и за что сегодня можно похвалить?
– Я тоже хочу вам что-то сказать, но я зашифровала свое слово. Чтобы его отгадать, нужно расположить бабочек в том порядке, в котором идут цвета радуги. (Спасибо)
Д/З начертить любой прямоугольник и найти его площадь
Общие сведения
В различных задачах с физико-математическим уклоном приходится вычислять площадь прямоугольника. Однако формула расчета применяется не только в математике и физике, но и во время ремонтных работ. Например, следует посчитать количество расходных материалов, которое зависит от квадратуры комнаты или здания.
Очень важно не только знать основные соотношения, но и корректно переводить единицы измерения из одной в другую. От знаний полностью зависит экономия денежных средств. Например, при клейке обоев в комнате требуется определенное количество рулонов. Это количество можно купить в строительном магазине «на глаз» или рассчитать квадратуру комнаты. Во втором случае можно существенно сэкономить. Для того чтобы посчитать квадратные метры помещения, нужно вычислить его площадь.
Площадь фигуры
Для вычисления значения двухплоскостной размерности фигуры применяется интегральный метод. Однако бывают частные случаи, когда вычислять интеграл необязательно. Существуют определенные формулы, полученные с помощью интегрального метода. Чтобы ими воспользоваться, нужно просто подставить числовые значения сторон.
Нахождение площади получило широкое распространение в физике. Например, для вычисления электрического сопротивления нужно найти площадь поперечного сечения проводника. Она зависит от его формы. Площадь можно вычислить и у объемной поверхности, но для этого применяется интегрирование.
Единицы измерения
При решении задач на нахождение значения площади нужно знать единицы ее измерения. Кроме того, следует правильно выполнять перевод одной единицы в другую. В системе исчисления используются квадратичные единицы измерения. За основу следует брать размер стороны прямоугольника. Например, при указании площади в кв. м нужно измерять в метраже стороны объекта. Это стандартная единица измерения площади.
Существуют также производные единицы. Самой маленькой из них является квадратный миллиметр (кв. мм или мм 2 ). В некоторой литературе или программировании можно встретить такую запись: sqr (m), которая означает квадратный метр. Основные производные единицы площади:
Последние применяются для измерения земельного участка. Однако необязательно их все помнить. Они легко выводятся при помощи простейших математических вычислений. Например, для выполнения расчетов нужно перевести кв. м в кв. см. Однако человек мог забыть, сколько см 2 в квадратном метре. Следует взять метрическую форму (1 м = 100 см). Затем нужно возвести обе части выражения в квадрат: 1 м 2 = 100 * 100 = 10000 (см 2 ).
Информация о прямоугольнике
Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.
Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.
Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.
Свойства и признаки
Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:
Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают. Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:
Однако свойств и признаков фигуры недостаточно для решения задач. Следует знать основные соотношения и формулы.

Периметр и размерность
Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + [2 * (2d 2 — 2a 2 )]^(1/2) и P = 2b + [2 * (2d 2 — 2b 2 )]^(1/2).
Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.
Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * [p * (p — a) * (p — b) * (p — d)]^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.
Примеры решения
Задачи на нахождение площади применяются в нескольких дисциплинах. В геометрии применяются различные комбинации, при которых известны некоторые величины:
Для расчета расходных материалов и площади поперечного сечения проводника можно всегда измерить стороны прямоугольника. Существует два способа нахождения: автоматизированный и ручной. В первом случае используется специализированное программное обеспечение. Однако вовсе не обязательно применять сложные алгоритмы и программные модули, поскольку формула является очень простой. Для расчета специалисты рекомендуют применять онлайн-калькулятор.
При ручном режиме расчета нужно подставлять значения в формулу. После этого выполнять вычисления. Возможна и оптимизация процесса вычисления. Для этой цели рекомендуется использовать Excel. Приложение входит в состав стандартного офисного пакета MS Office.

Геометрия на плоскости
Задача сводится к тому, что необходимо высчитать S, зная размеры сторон (a = 25 и b = 10). В этом случае следует воспользоваться базовой формулой: S = a * b = 25 * 10 = 250 (ед 2 ). В ответе указывается условная единица измерения, поскольку явная не указана в условии задачи.
Еще один вариант задания немного сложнее предыдущего. Он имеет следующее условие: одна из сторон прямоугольника равна 6 м и диагональ 10 м. Нужно найти площадь прямоугольника. Формулой в этом случае является теорема Пифагора. Треугольник, который образуется при проведении диагонали, считается прямоугольный (неравносторонний, а разносторонний). Решается задача следующим образом:
Находится неизвестная сторона: b =(d 2 — a 2 )^(1/2) = (100 — 36)^(1/2) = 8 (м).
Площадь (произведение сторон): S = 6 * 8 = 48 (м 2 ).
Можно использовать двойную формулу Герона, однако метод усложняет вычисления. Для сравнения скорости и объема вычислений следует решить задачу вторым способом:
Значение площади будет вычисляться таким образом: S = 2 * [12 * (12−6) * (12−8) * (12−10)]^(1/2) = 2 * 24 = 48 (м 2 ).
Второй способ считается неправильным, поскольку необходимо во всех задачах оптимизировать вычисления. Сложным типом задачи, кроме интегрирования, считается нахождение площади, когда неизвестны стороны, а известна только диагональ (10). Известно также, что одна из сторон больше другой на 3 метра. В этом случае надо выражать одну сторону через другую. Алгоритм решения следующий:
Раскрыть скобки: x 2 — 3x — 10 = 0.
Нахождение дискриминанта: D = b 2 — 4* a * c = 9 — (4 * 10) 2 ). Однако берется не исходное значение, а приближенное. Его нужно округлять только в большую сторону, т. е. править 3,75 на значение 4. Следует руководствоваться таким правилом: результат округляется в большую сторону.
Таким образом, для расчета площади прямоугольника можно воспользоваться формулой, а не выполнять интегрирование. Однако перед этим нужно внимательно изучить основные понятия и математические отношения.

Урок математики для 2 класса «Площадь прямоугольника»
(Образовательная система «Школа 2100»)
учитель начальных классов
МАОУ «СОШ № 102 с углубленным отдельных изучением предметов»
Еремеева Наталья Николаевна
Тип урока Урок открытия нового знания (технология деятельностного метода)
Дидактическая цель
Деятельностная цель : формирование способности учащихся к новому способу действия: использование правила для вычисления площади прямоугольника (квадрата).
Образовательная цель:
1.сформировать умение находить площадь прямоугольника и квадрата;
2. углубить и расширить представление детей о плоскостных фигурах;
3. совершенствовать вычислительные навыки, умение решать текстовые задачи.
Учебные задачи, направленные на достижение личностных результатов обучения:
формирование уважительного отношения к иному мнению, к иной точке зрения;
формирование логическое мышление, наблюдательности, интуиции, упорства, воли для достижения цели, самостоятельность
формирование умения обобщать, конкретизировать.
Учебные задачи, направленные на достижение метапредметных результатов обучения:
формирование умения работать с новой информацией по теме (отбирать, выделять, обобщать);
формирование умения выстраивать речевые высказывания;
формирование умений работать в статичных группах и парах (коммуникативные УУД);
формирование чувства коллективизма
формирование начальных форм рефлексии (регулятивные УУД).
Учебные задачи, направленные на достижение предметных результатов обучения:
освоение знаний по теме: «Площадь прямоугольника».
вывести правило для нахождения площади прямоугольника
научиться применять правило для решения задач
совершенствовать вычислительные навыки
научиться применять правило для расчета площади поверхности прямоугольной формы
Оборудование: проектор, компьютер, линейка у каждого ученика, рулетка на группу.
Материал ведения урока
УУД на этапах урока
1. Организационный момент.
2. Формулирование темы, цели урока, планирование.
3. Актуализация опорных знаний.
4.Работа над новым материалом.
4. Исследовательская работа.
5. Применение знаний в жизненных ситуациях.
7. Итог урока. Рефлексия.
Наш урок мне бы хотелось начать со слов:
«Только то и приятно, что трудно достать» М.Твен
Как эти слова можно отнести к нашему уроку математики?
Я думаю, мы сегодня испытаем удовольствие от работы.
Вам известен автор этих слов?
Внимательно посмотрите на экран.
Кто из вас догадался, какая тема нашего урока?
(нахождение площади прямоугольника)
Тема: Площадь прямоугольника.
Тема совершенно новая для нас?
Что знаете о площади?
Как мы находили площадь фигуры?
Может им воспользоваться Том?
Какую цель поставим на урок?
Цель известна, как будем достигать?
Составим план достижения цели.
У вас на парте в папке две геометрические фигуры. Рассмотрите их. Что можете сказать?
(2 прямоугольника разного цвета,
с размерами 5 и 6 см; 8 и 4 см)
Что можно сказать об их площади?
Площадь какого больше?
Может им воспользоваться Том?
Может быть, кто-то догадался, как найти площадь более удобным способом?
Посчитайте количество квадратных см по длине.
Посчитайте количество квадратных см по ширине.
(учитель проецирует через веб камеру на экран)
Каждый составьте алгоритм нахождения площади прямоугольника. Подумайте секунду.
Сравните свой алгоритм с эталоном.
Согласно плану, какой следующий шаг?
Найдите площадь поверхности
учебника математики и папки с заданиями.
Сравни свою работу с эталоном.
Перенесемся примерно на 150 лет назад в американскую школу, в которой учится Том Сойер.
Сравните работу с эталоном
Наш урок близится к концу, что бы каждый смог ответить на вопрос: достиг ли он цели, предлагаю выполнить небольшую самостоятельную работу.
Выбери для себя задание по силам и выполни его
Вернемся к цели урока. Достиг ли каждый из вас цели?
Как вы чувствовали себя на уроке?
Какие задания вызвали большую сложность?
Над чем вам еще нужно поработать?
У кого можно попросить помощи?
Устные ответы детей.
(мы испытываем удовлетворение от своей работы, когда самостоятельно преодолеваем трудности и достигаем цели)
«Приключения Тома Сойера»
Высказывания детей, устные ответы.
Тема не новая, мы умеем находить площадь фигуры.
Научиться находить площадь удобным способом;
Применять эти знания в жизни.
Составление плана на урок.
Сразу ответить на вопрос нельзя, т.к на глаз определить невозможно и методом наложения не получается.
Разбить на см квадратные.
Разбивают на квадратные см и сравнивают площади.
Предположения высказывают устно.
Что бы найти площадь нужно длину умножить на ширину.
Работа в группе над алгоритмом.
Сравнивают свой алгоритм с эталоном.
Капитан подводит итог по этой работе.
Справилась группа или нет и почему, где ошибка в работе.
Ребята находят площадь поверхности предметов.
Анализируют результат своей работы.
Получилось, потому что мы правильно измерили,
Не получилось, потому что….
Распределяют роли, составляют план решения.
Производят измерения(с помощью рулетки).
Анализируют результат работы в группе.
Получилось, потому что мы правильно составили план,
Не получилось, потому что….
Самостоятельная работа по уровням.
Самопроверка по образцу.
Не достиг, потому что…
1.Формируем умение слушать и понимать других.
2.Формируем умение строить речевое высказывание в соответствии с поставленными задачами.
3.Проговаривание последовательности действий на уроке.
1.Умение слушать и вступать в диалог с учителем, сверстниками.
2.Умение выражать свои мысли.
1.Распознавать и соотносить реальные объекты с моделями пространственных геометрических фигур.
3.Строить продуктивное взаимодействие и сотрудничество со сверстниками.
4.Формируем и отрабатываем умение согласованно работать в микро группах и коллективе.
1.Распознавать геометрические фигуры.
2.Выделять признаки этих фигур.
3.Обобщать способы сравнения площади фигур.
4.Нахождение площади, способом разбиения на квадратные см.
Умение структурировать знания.
Умение строить речевое высказывание.
Выбор наиболее эффективных способов решения.
Контроль и оценка процесса и результатов действия.
Проговаривание последовательности действий.
Совместная эмоциональная оценка деятельности группы на уроке.
Отличие верно выполненного задания от неверного.
1.Научатся вычислять площадь фигуры.
2.Совершенствуют умение измерять длину и ширину предметов
Различать длину и ширину
3.Примененять правило для решения задачи.
Формируем эмоциональное отношение к школе и учебной деятельности.
Формируем общее представление о моральных нормах поведения.
1.Научатся анализировать задачу, устанавливать связь между величинами,взаимосвязь между условием и вопросом задачи.
2.Решать задачи в 2 действия арифметическим способом.
3.Планировать ход решения задачи.
4.Оценивать правильность хода решения задачи и реальность ответа на вопрос задачи.
1.Умение слушать и вступать в диалог.
2.Умение выражать свои мысли
строить продуктивное взаимодействие и сотрудничество со сверстниками.
3.Планировать совместную деятельность.
1.Применение полученных знаний в жизненных ситуациях
2.Учимся адекватно себя оценивать
1.Умение ориентироваться в социальных ролях и межличностных отношениях
2.Проговаривание последовательности действий.
3. Совместная эмоциональная оценка деятельности группы на уроке.
4.Отличие верно выполненного задания от неверного.
1.Применение полученных знаний в жизненных ситуациях.
2.Учимся адекватно себя оценивать.
1.Совместная эмоциональная оценка деятельности класса на уроке.
2.Отличие верно выполненного задания от неверного.
3.Рефлексия, которая тесно связана с целью урока.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
«Выдержка из материала:
Урок математики «Площадь прямоугольника»
Наш урок мне бы хотелось начать со слов: «Только то и приятно, что трудно достать» М. Твен
Как эти слова можно отнести к нашему уроку математики? Я думаю, мы сегодня испытаем удовольствие от работы. Вам известен автор этих слов? Внимательно посмотрите на экран. Слайд с эпизодом. Кто из вас догадался, какая тема нашего урока? (нахождение площади прямоугольника)
Тема: Площадь прямоугольника.
Тема совершенно новая для нас? Что знаете о площади? Как мы находили площадь фигуры? Удобный способ? Может им воспользоваться Том? Какую цель поставим на урок?
Цель известна, как будем достигать? Составим план достижения цели.
У вас на парте в папке две геометрические фигуры. Рассмотрите их. Что можете сказать? (2 прямоугольника разного цвета, с размерами 5 и 6 см; 8 и 4 см) Что можно сказать об их площади? Площадь какого больше? Как сравнить? Удобный способ? Может им воспользоваться Том?
Может быть, кто-то догадался, как найти площадь более удобным способом? Посчитайте количество квадратных см по длине. Чему равно? Посчитайте количество квадратных см по ширине. Чему равно? (учитель проецирует через веб камеру на экран) Каждый составьте алгоритм нахождения площади прямоугольника. Подумайте секунду. Обсудите в группе. Сравните свой алгоритм с эталоном.
Согласно плану, какой следующий шаг? Найдите площадь поверхности учебника математики и папки с заданиями.
Сравни свою работу с эталоном.
Перенесемся примерно на 150 лет назад в американскую школу, в которой учится Том Сойер.
Сравните работу с эталоном
Наш урок близится к концу, что бы каждый смог ответить на вопрос: достиг ли он цели, предлагаю выполнить небольшую самостоятельную работу. Выбери для себя задание по силам и выполни его Проверь себя.
Вернемся к цели урока. Достиг ли каждый из вас цели? Как вы чувствовали себя на уроке? Какие задания вызвали большую сложность? Над чем вам еще нужно поработать? У кого можно попросить помощи? Устные ответы детей. (мы испытываем удовлетворение от своей работы, когда самостоятельно преодолеваем трудности и достигаем цели) М. Твен автор книги «Приключения Тома Сойера»
Высказывания детей, устные ответы. Устная работа. Тема не новая, мы умеем находить площадь фигуры.
Цель:
«Устная работа. Составление плана на урок. Работа в парах. Устно.
Это прямоугольники, т. к у них противоположные стороны равны а углы прямые. Сразу ответить на вопрос нельзя, т. к на глаз определить невозможно и методом наложения не получается. Разбить на см квадратные. Разбивают на квадратные см и сравнивают площади. Предположения высказывают устно. Равно длине. Равно ширине. Что бы найти площадь нужно длину умножить на ширину. Работа в группе над алгоритмом.
Сравнивают свой алгоритм с эталоном. Капитан подводит итог по этой работе. Справилась группа или нет и почему, где ошибка в работе. Применение алгоритма. Работа в паре. Ребята находят площадь поверхности предметов. Анализируют результат своей работы.
Делают ввод: Получилось, потому что мы правильно измерили, посчитали. Не получилось, потому что…. Работа в группе. Распределяют роли, составляют план решения. Производят измерения(с помощью рулетки). Вычисляют площади. Анализируют результат работы в группе.
Делают ввод: Получилось, потому что мы правильно составили план, измерили, посчитали, сравнили. Работали слаженно. Не получилось, потому что….
Самостоятельная работа по уровням.
Самопроверка по образцу.
Устные ответы. Достиг, потому что… Не достиг, потому что…
Коммуникативные УУД
Регулятивные УУД
Коммуникативные УУД
Предметные результаты
Предметные результаты
Познавательные УУД
Регулятивные УУД
Предметные
Личностные УУД
Предметные
Коммуникативные УУД
Личностные УУД
Регулятивные УУД
Личностные УУД
Регулятивные УУД