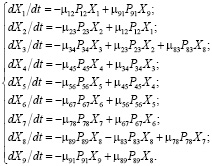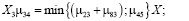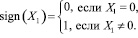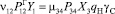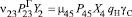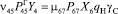Что такое плечо в перевозках

Логистическое плечо (часть 1)

Логистическое плечо

Логистическое плечо – расстояние от места хранения товара или от пункта загрузки до пункта выгрузки или получения товара. Различают «короткое плечо» и «длинное плечо».

«Длинное плечо» означает перевозку грузов на большие расстояния, которые груз проходит в течение нескольких дней, например, международные грузовые перевозки (https://www.shneider.by/).

Длительность хранения груза определяет длину плеча в днях. В связи с чем скоропортящиеся грузы (с.-х. продукция, молочные продукты и фруктовые концентраты) перевозят на длину плеча с учетом времени дозревания фруктов, сроков хранения других продуктов.

Кроме того на скорость поставки несырьевых товаров влияет технология их перевозки (https://portnews.ru/):

— альтернативой для сыпучих грузов (сахара-сырца и т.д.) является их перевозка в универсальных крупнотоннажных контейнерах с использованием вкладыша.

— альтернативой для наливных грузов (растительных масел и т.д.) является их перевозка во флекситанках.

Грамотно выстроенная логистика (от управления складскими запасами до их доставки покупателю) существенно снижает издержки в цепочке поставок (https://www.trn.ua/, https://sys4tec.com/).

Определение маршрута международной перевозки

Подобрать маршрут международной перевозки можно с использованием транспортно-логистической платформы на сайте http://webcomtrans.com/, а стоимость международной перевозки (авиа-, море, авто-) на сайте http://www.ecargoworld.com/.

Определить стоимость перевозки, место нахождения морского судна (контейнера) и иное можно на сайте http://advanceshipping.ru/.

Подобрать плечо доставки автомобильным транспортом с учетом оптимизации его стоимости, а также контролировать всю цепь поставки груза с момента подтверждения водителем рейса до полной выгрузки машины с передачей документов напрямую от водителя можно с использованием приложения «Умная логистика» (https://b2b-logist.com/, https://plus.rbc.ru/).

Авиаперевозки – самый быстрый и дорогой способ доставки.

Автомобильные грузоперевозки – это компромисс между ценой и скоростью доставки. Они присутствуют в большинстве логистических схем и являются неотъемлемой частью доставки от двери до двери.

Морские грузоперевозки – наиболее дешевый и медленный способ доставить груз. Перевозка по морю позволяет обойти несколько таможенных постов, что значительно удешевляет процесс, однако доставка груза в порт, складские процессы, непосредственно перемещение и выгрузка товара занимают большой объем времени. Морские перевозки часто используются при доставке груза из Европы в Азию и обратно, так как судно проходит через крупные порты, на которых может забрать дополнительный груз.

Подробнее о совместимости внешнеэкономической поставки и договора перевозки, особенностях базисов поставки в редакциях Инкотермс 2010 и Инкотермс 2020 см. в статьях Базисы поставки (часть 1) и Базисы поставки (часть 2).

Мультимодальные перевозки

При мультимодальной перевозке транспортировка грузов по одному договору выполняется двумя и более видами транспорта; перевозчик несёт ответственность за всю перевозку, даже если эта транспортировка производится разными видами транспорта.

Развитость транспортных коридоров, наличие ж.-д. и автомобильных подходов к морским портам и аэропортам позволяет организовать на их базе мультимодальные грузовые хабы.

В свою очередь это позволяет перевозить контейнерные грузы, а также уменьшает накопление грузов на складах временного хранения до объема требуемой партии, простои в портах и на узловых ж.-д. станциях (https://rg.ru/, https://plus.rbc.ru/, https://www.popmech.ru/).

Таможенные перевозчики, брокеры и портовые стивидоры

Перечень транспортно-логистических компаний (таможенных перевозчиков), выполняющих перевозку экспорт-импортных грузов представлен на сайтах https://customsforum.ru/, https://www.tks.ru/.

Одними из крупнейших таможенных перевозчиков являются:

Перечень логистических компаний России см. по ссылке https://logirus.ru/.

Как правило таможенные перевозчики выполняют также экспедирование груза, являясь таможенными брокерами. Перечень таможенных брокеров российского реестра представлен на сайтах https://www.tks.ru/, https://customsforum.ru/.

Перечень стивидорных компаний, оказывающих перевалку грузов в российских морских портах можно увидеть по ссылкам:

Источник

Что такое транспортное плечо?

Это понятие вводится при перевозке/доставке грузов. Пользуются им компании-перевозчики (логистические компании), отделы снабжения и сбыта предприятий и др.

Транспортным плечом называется расстояние между начальным и конечным пунктами доставки груза.

Зная транспортное плечо, вид транспорта, можно рассчитать время и стоимость доставки товара.

Транспортное плечо, это расстояние перевозки грузов. Как правило, этот термин употребляется, при перевозке грузов по постоянному маршруту. Например, гравий перевозится от горного карьера до растворо-бетонного узла, или руда перевозится от шахты к горнообогатительному комбинату.

Термин транспортное число очень часто можно встретить в статьях о логистике, о планировании перевозок и бизнеса и журналах.

Транспортное плечо бывает короткое и большое. Это всего-навсего расстояние от пункта А до пункта Б: от поставщика до потребителя, обычно.

Этот термин из логистики. Обозначает расстояние между пунктом отправления товара и пунктом назначения. Также в экономике часто выражается в стоимостном эквиваленте, чтобы можно было проводить сравнительную характеристику и выбирать наиболее оптимальный и выгодный вариант.

Уже ни первый день многие спорят, что лучше и какой сервис заказа удобнее в целом.

Что же попробуем выделить их плюсы и минусы и постараться понять, чем же лучше пользоваться и можно ли вот так быстро определить, какой из многомиллионных брендов удобнее и технологичнее.

По моему скромному мнению дизайн мобильного приложения компании убер уже навевает на что-то из 90х, хотя и может показаться современным, но очень даже не удобен, это явно стоит отнести к его основным минусам.

Если же говорить именно о качестве сервиса, то скоре всего в Яндексе работают те самые гастрабайтеры, и не понятные личности, поэтому о качестве обслуживания там если и можно судить, то оно явно будет ниже, чем в убере, потому что там к подбору водителей относятся более трепетно.

Опять же в компании Убер реже скачут цены, и нет такого, что как в Яндексе в час-пик, ценник повышается в 2 или 3 раза.

Но все же минусов хватает, если же отбросить минус дизайна приложения убер и в целом доступности в нем различных функций, то скорее всего старый добрый Убер лучше и удобнее, так что я бы выбрал его, отличия я описал уже выше.

Также благодаря повышенной мощности и увеличенной секционности поезд нового поколения «Ермак» способен перевозить удлинённые и сверхтяжёлые составы, что делает его практически незаменимым во многих регионах России.

Источник

транспортное плечо

3.13 транспортное плечо : Расстояние между начальным и конечным пунктами доставки груза.

Смотреть что такое «транспортное плечо» в других словарях:

Газпром нефть — (Gazprom neft) Компания Газпром нефть, собственники и руководство компании, создание и развитие Газпром нефти Информация о компании Газпром нефть, собственники и руководство компании, создание и развитие Газпром нефти Содержание Содержание «»… … Энциклопедия инвестора

СП 105.13330.2012: Здания и помещения для хранения и переработки сельскохозяйственной продукции — Терминология СП 105.13330.2012: Здания и помещения для хранения и переработки сельскохозяйственной продукции: 3.1 бункер : Саморазгружающееся емкостное сооружение с высотой вертикальной части, не превышающей полуторного минимального размера в… … Словарь-справочник терминов нормативно-технической документации

Энакин Скайуокер — Персонаж «Звёздных войн» Энакин Скайуокер Деятельность Рыцарь Джедай, член Совета Джедаев, Командор Республиканской а … Википедия

Франция — (France) Французская Республика (République Française). I. Общие сведения Ф. государство в Западной Европе. На С. территория Ф. омывается Северным морем, проливами Па де Кале и Ла Манш, на З. Бискайским заливом… … Большая советская энциклопедия

Силовая неоднородность шины — Силовая неоднородность шины это динамически механические свойства пневматических шин, которые четко обозначены набором стандартов измерений и условий проведения испытаний, принятых производителями шин и автомобилей по всему миру. Эти… … Википедия

1.1.1.1. — 1.1.1.1. Предложения, отображающие ситуацию однонаправленного движения, ориентированного относительно исходного и конечного пунктов Типовая семантика Человек, группа лиц, живое существо (животное, птица, рыба, насекомое), транспортное средство,… … Экспериментальный синтаксический словарь

Велосипед — Привод Мускульная сила водителя П … Википедия

Велик — Велосипед Привод Мускульная сила водителя Период с середины XIX века Скорость 268 км/ч на ровной поверхности в воздушном колоколе (рекорд)[1] Область применения … Википедия

Велосипеды — Велосипед Привод Мускульная сила водителя Период с середины XIX века Скорость 268 км/ч на ровной поверхности в воздушном колоколе (рекорд)[1] Область применения … Википедия

Костотряс — Велосипед Привод Мускульная сила водителя Период с середины XIX века Скорость 268 км/ч на ровной поверхности в воздушном колоколе (рекорд)[1] Область применения … Википедия

Источник

Что такое плечо в перевозках

Своевременные бесперебойные массовые автомобильные перевозки различных грузов предполагают наличие надежного автомобильного подвижного состава [1]. Вопросы его эксплуатационной надежности определяются различными факторами [3], в том числе структурой и свойствами материалов деталей и элементов конструкций автомобилей 4.

При этом в процессе решения многих задач автомобильного транспорта, связанных с обоснованием и выбором рациональной организации перевозок, приходится сталкиваться с ситуацией, когда исследуемая система оказывается настолько сложна, что обычное решение задачи невозможно, а проведение экспериментальных исследований или натуральных испытаний требует больших затрат времени и средств. Одной из эффективных мер по преодолению указанных выше трудностей является применение методов математического моделирования, позволяющих решать широкий круг задач автомобильного транспорта.

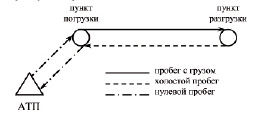
В качестве объекта моделирования примем работу группы автомобилей, снабжающих некоторым видом груза склад клиента-потребителя, на маятниковом маршруте с обратным незагруженным пробегом. В этом случае моделированию подлежат два взаимосвязанных процесса: процесс перемещения автомобилей по маршруту и процесс перемещения единиц груза со склада клиента-поставщика на склад клиента-потребителя, а также процесс накопления и расходования груза на этом складе.

Построение имитационной математической модели

Построение имитационной математической модели транспортного процесса начнем с той ее части, которая моделирует перемещение автомобилей по маршруту. Отметим, что в процессе выполнения сменно-суточного задания любой автомобиль в любой момент времени может находиться в одном из девяти состояний (рис. 1):

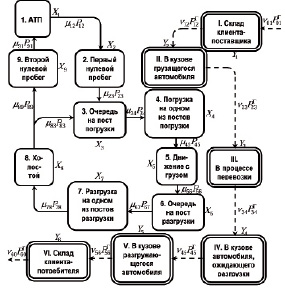
Реальному процессу перемещения автомобилей по маршруту в модели будет соответствовать последовательный переход автомобилей из одного состояния в другое. Тогда данному процессу можно поставить в соответствие некоторый марковский процесс перехода объекта управления (автомобилей и единиц груза) из одного состояния в другое [8], определяемый графом переходов анализируемой системы, представленном на рис. 2.

Рис. 1. Схема работы маятникового маршрута с обратным незагруженным пробегом

Рис. 2. Совмещенный граф перемещения автомобилей и единиц груза

Блоками с одинарным контуром на рис. 2 обозначены возможные состояния автомобилей, а сплошными стрелками направления перехода из одного состояния в другое. Через Х_i (i = 1,2. 9) на рис. 2 обозначено мгновенное количество автомобилей в соответствующем i-ом состоянии, через m – интенсивность перехода одного автомобиля из данного i-гo в последующее j-ое состояние, а через Р_ij– вероятность такого перехода. Под интенсивностью перехода одного автомобиля из данного состояния в последующее будем понимать величину, обратную времени пребывания автомобиля в i-ом состоянии, т.е.

, (1)

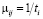
где t_i – время пребывания автомобиля в i-ом состоянии.

Каждому состоянию графа переходов системы будет соответствовать дифференциальное уравнение вида

. (2)

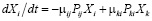
Это уравнение определяет скорость изменения количества автомобилей в рассматриваемом состоянии (dX_i/dt) как разность между суммарной интенсивностью перехода автомобилей в данное i-ое состояние из предыдущего k-го и суммарной интенсивностью перехода из данного i-гo в последующее j-ое состояние [2]. Тогда рассматриваемому графу переходов будет соответствовать система из девяти дифференциальных уравнений:

Для интегрирования этой системы необходимо задать значения вероятностей Р_ij и интенсивностей μ_ij переходов из одного состояния в другое, а также начальные условия интегрирования.

Вероятности переходов автомобилей из одного состояния в другое используем для управления движением автомобилей. Для этого будем рассматривать их как булевы переменные, принимающие значение 0, если данный переход из одного состояния в другое необходимо запретить, и 1, если такой переход разрешен.

Будем считать, что вероятности переходов P₂₃, P₃₄, P₄₅, P₅₆, P₆₇, P₇₈ и P₉₁ всегда равны единице. Вероятности P₁₂, P₈₃ и P₈₉ могут принимать значения 0 или 1 и связаны между собой следующей зависимостью: если P₁₂ = 0, то P₈₉ может принимать значения 0 или 1, если P₈₃ = 1, то P₈₉ может иметь только нулевое значение, и наоборот. Для вероятностей P₈₃ и P₈₉ установим следующую зависимость: P₈₃ = 0, если P₈₉ = 1, и P₈₃ = 1, если P₈₉ = 0.

Перейдем теперь к определению интенсивностей переходов из одного состояния в другое μ_ij. Отметив, что интенсивность перехода автомобиля из какого-либо состояния есть величина обратная времени пребывания автомобиля в этом состоянии, выразим ее через значения параметров транспортного процесса [2]. Проще всего это сделать для состояний, отражающих процесс перемещения автомобиля по маршруту (состояния 2, 5, 8, 9). При этом соответствующие интенсивности примут следующие значения:

(4)

где l₀ – длина нулевого пробега (расстояние от склада поставщика до автотранспортного предприятия);

l_М – длина маршрута (расстояние от склада поставщика до склада потребителя);

v_ТГ – скорость движения автомобиля с грузом;

v_ТХ– скорость движения автомобиля без груза.

Несколько сложнее определить интенсивности μ₄₅ и μ₇₈ переходов из состояний погрузки и выгрузки. В общем случае с увеличением числа автомобилей в этих состояниях в пределах от X_i = 0 до X_i = mi (где m_i – число постов погрузки или выгрузки в рассматриваемом состоянии) суммарная интенсивность перехода μ_ij X_i растет от нуля до значения

, (5)

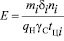
где δ_i – грузоподъемность погрузочной (или разгрузочной) машины в рассматриваемом состоянии;

n_i – количество погрузочных (или разгрузочных) машин на одном посту;

q_Н – грузоподъемность автомобиля;

γ_C – коэффициент использования грузоподъемности автомобиля;

t_Цi – время цикла погрузочной (или разгрузочной) машины.

При дальнейшем увеличении числа автомобилей в соответствующем состоянии появляется очередь (простой в ожидании погрузки или выгрузки) и величина X_i μ_ij остается неизменной, как показано на рис. 3.

Рис. 3. График зависимости суммарной интенсивности переходов автомобилей из состояния погрузки или выгрузки от числа автомобилей

Приведенному на рис. 3. графику соответствует уравнение:

. (6)

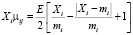
Подставляя сюда значение Е и производя несложные преобразования, получим:

.(7)

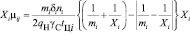
Тогда интенсивности μ₄₅ и μ₇₈ переходов из состояний погрузки и выгрузки примут вид:

. (8)

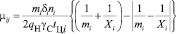
Однако, поскольку ожидание погрузки и разгрузки мы выделили в отдельные состояния, количество автомобилей в них не будет превышать число постов в этих состояниях, и интенсивности μ₄₅ и μ₇₈ окончательно примут значения:

; . (9)

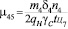
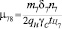
Так как на посты погрузки или выгрузки автомобили будут поступать либо по мере освобождения постов (при наличии очереди), либо по мере прибытия в пункт погрузки-выгрузки (при отсутствии очередей в этих состояниях), то суммарные интенсивности переходов автомобилей из состояний ожидания погрузки и выгрузки в данном случае могут быть определены следующим образом:

. (10)

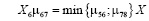
Интенсивность перехода автомобилей из состояния 1 (в АТП) в состояние 2 (в первом нулевом пробеге) будет зависеть от графика выпуска автомобилей на линию и может быть вычислена по формуле:

, (11)

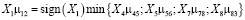
где

Подставляя полученные значения интенсивностей и вероятностей в систему дифференциальных уравнений перемещения автомобилей по маршруту (3), получим в окончательном виде математическую модель перемещения автомобилей. Процесс непрерывного интегрирования приведенной системы дифференциальных уравнений (3) соответствует процессу последовательного перемещения автомобилей из одного состояния в другое. Точность моделирования при этом определяется величиной выбранного периода интегрирования: чем меньше этот период, тем точнее моделирование.

Одновременно с перемещением автомобилей по маршруту происходит процесс перемещения груза, определяющий выполнение сменно-суточного задания. Математическая модель перемещения груза строится способом, аналогичным тому, что был применен для моделирования перемещения автомобилей [8].

Каждая единица груза может находиться в любой момент времени в одном из шести состояний:

Реальному процессу перемещения единиц груза в модели будет соответствовать последовательный переход из одного состояния в другое [2]. Граф переходов анализируемой системы представлен на рис. 2. Блоками с двойным контуром обозначены возможные состояния единиц груза, а пунктирными стрелками направления перехода из одного состояния в другое.

На этом графе римскими цифрами обозначены возможные состояния единиц перевозимого груза в соответствии с приведенным перечнем состояний. 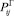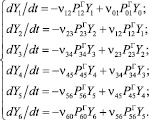Через Y_i обозначено количество единиц груза в i-ом состоянии (под состоянием с индексом i = 0 подразумевается любое внешнее по отношению к рассматриваемой системе состояние), через v_ij – интенсивность перехода единицы груза из данного i-го в последующее j-e состояние, а через – вероятность такого перехода. Отметим, что интенсивности v₀₁ и v₆₀ определяют соответственно скорость поступления груза на склад клиента-поставщика и расходование груза со склада клиента-потребителя; они должны быть заданы в исходных данных. Тогда той части обобщенного графа переходов (рис. 2), которая описывает перемещение единиц груза, можно поставить в соответствие следующую систему из шести дифференциальных уравнений:

(12)

Для возможности совместного решения обоих полученных систем уравнений отметим, что перемещение груза определяется перемещением автомобилей. Произведем следующую замену:

(13)

.

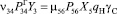
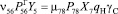
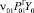
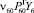
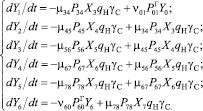
Величины и аналогичным образом через параметры системы уравнений перемещения автомобилей выражены быть не могут и, как уже отмечалось, должны быть определены в исходных данных. Тогда вторая система уравнений примет следующий вид:

(14)

Эти две системы дифференциальных уравнений (3), (15) и составляют основу создаваемой математической модели, а при совместном интегрировании имитируют перемещение по маршруту автомобилей и единиц груза.

Выводы

Предложенная математическая модель хотя и достаточно точна, но обладает рядом существенных недостатков:

Поэтому здесь необходимо применять метод имитационного моделирования, сущность которого в последовательной обработке описанных выше состояний с помощью математического аппарата и алгоритмов, реализуемых на ЭВМ.

Рецензенты:

Панов А.Ю., д.т.н., профессор, директор ИПТМ, Нижегородский государственный технический университет им. Р.Е. Алексеева (НГТУ), г. Нижний Новгород;

Молев Ю.И., д.т.н., профессор кафедры «Строительные и дорожные машины» (СДМ), Нижегородский государственный технический университет им. Р.Е. Алексеева (НГТУ), г. Нижний Новгород.

Источник