Что такое перемещение материальной точки

Кинематика. Перемещение и путь.

Перемещением в механике называют вектор (направленный отрезок прямой), соединяющий начальное и последующее положения тела.

Понятие вектора перемещения вводится для решения задачи кинематики – определить положение тела в пространстве в данный момент времени, если известно его начальное положение.

Допустим, точка М движется по криволинейной траектории и в некоторые моменты времени t₁ и t₂ оказывается в точках М₁ и М₂ соответственно. Вектор соединяет эти два положения и является вектором перемещения. Если точку М₁ задать радиус-вектором , а точка М₂ – радиус-вектором , то вектор перемещения будет равен разности этих двух векторов:

Путь – это длина участка траектории, пройденного телом за данный промежуток времени. В общем случае модуль вектора перемещения не равен длине пути, пройденного телом за некоторый промежуток времени, поскольку траектория может быть криволинейной, а тело может менять направление движения.

Модуль вектора перемещения и путь могут быть равны только при прямолинейном движении в одном направлении. При изменении направления прямолинейного движения модуль вектора перемещения будет меньше пути.

При криволинейном движении модуль вектора перемещения тоже меньше пути, поскольку хорда всегда меньше дуги, которую она стягивает.

Источник

Механическое движение. Траектория. Путь. Перемещение

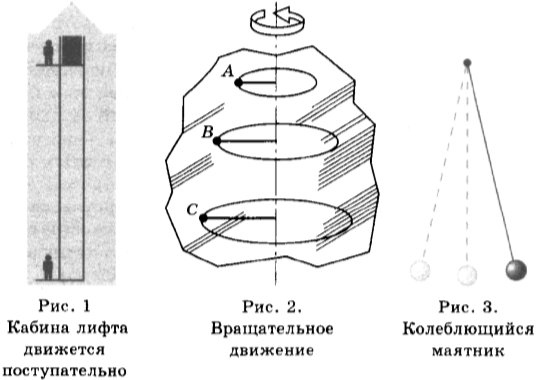
1. Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. Существуют различные виды механического движения. Если все точки тела движутся одинаково и любая прямая, проведённая в теле, при его движении остаётся параллельной самой себе, то такое движение называется поступательным (рис. 1).

Точки вращающегося колеса описывают окружности относительно оси этого колеса. Колесо как целое и все его точки совершают вращательное движение (рис. 2).

Если тело, например шарик, подвешенный на нити, отклоняется от вертикального положения то в одну, то в другую сторону, то его движение является колебательным (рис. 3).

2. В определение понятия механического движения входят слова «относительно других тел». Они означают, что данное тело может покоиться относительно одних тел и двигаться относительно других тел. Так, пассажир, сидящий в автобусе, движущемся относительно зданий, тоже движется относительно них, но покоится относительно автобуса. Плот, плывущий по течению реки, неподвижен относительно воды, но движется относительно берега (рис. 4). Таким образом, говоря о механическом движении тела, необходимо указывать тело, относительно которого данное тело движется или покоится. Такое тело называют телом отсчёта. В приведённом примере с движущимся автобусом в качестве тела отсчёта может быть выбран какой-либо дом, или дерево, или столб около автобусной остановки.

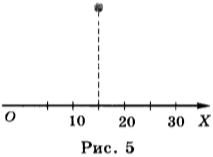
Для определения положения тела в пространстве вводят систему координат, которую связывают с телом отсчёта. При рассмотрении движения тела вдоль прямой линии используют одномерную систему координат, т.е. с телом отсчёта связывают одну координатную ось, например ось ОХ (рис. 5).

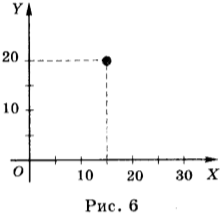
Если тело движется по криволинейной траектории, то система координат будет уже двухмерной, поскольку положение тела характеризуют две координаты X и Y (рис. 6). Таким движением является, например, движение мяча от удара футболиста или стрелы, выпущенной из лука.

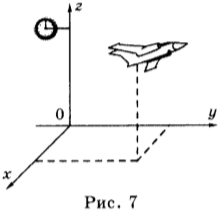
Если рассматривается движение тела в пространстве, например движение летящего самолёта, то система координат, связанная с телом отсчёта, будет состоять из трёх взаимно перпендикулярных координатных осей (OX, OY и OZ) (рис. 7).

Поскольку при движении тела его положение в пространстве, т.е. его координаты, изменяются с течением времени, то необходим прибор (часы), который позволяет измерять время и определить, какому моменту времени соответствует та или иная координата.

Таким образом, для определения положения тела в пространстве и изменения этого положения с течением времени необходимы тело отсчёта, связанная с ним система координат и способ измерения времени, т.е. часы, которые все вместе представляют собой систему отсчёта (рис. 7).

3. Изучить движение тела — это значит определить, как изменяется его положение, т.е. координата, с течением времени.

Если известно, как изменяется координата со временем, можно определить положение (координату) тела в любой момент времени.

Основная задача механики состоит в определении положения (координаты) тела в любой момент времени.

Чтобы указать, как изменяется положение тела с течением времени, нужно установить связь между величинами, характеризующими это движение, т.е. найти математическое описание движения или, иными словами, записать уравнение движения тела.

Раздел механики, изучающий способы описания движения тел, называют кинематикой.

4. Любое движущееся тело имеет определённые размеры, и его различные части занимают разные положения в пространстве. Возникает вопрос, как в таком случае определить положение тела в пространстве. В делом ряде случаев нет необходимости указывать положение каждой точки тела и для каждой точки записывать уравнение движения.

Так, поскольку при поступательном движении все точки тела движутся одинаково, то нет необходимости описывать движение каждой точки тела.

Движение каждой точки тела не нужно описывать и при решении таких задач, когда размерами тела можно пренебречь. Например, если нас интересует, с какой скоростью пловец проплывает свою дистанцию, то рассматривать движение каждой точки пловца нет необходимости. Если же необходимо определить действующую на мяч выталкивающую силу, то пренебречь размерами пловца уже нельзя. Если мы хотим вычислить время движения космического корабля от Земли до космической станции, то корабль можно считать единым целым и представить в виде некоторой точки. Если же рассчитывается режим стыковки корабля со станцией, то, представив корабль в виде точки, решить эту задачу невозможно.

Таким образом, для решения ряда задач, связанных с движением тел, вводят понятие материальной точки.

Материальной точкой называют тело, размерами которого можно пренебречь в условиях данной задачи.

В приведённых выше примерах материальной точкой можно считать пловца при расчёте скорости его движения, космический корабль при определении времени его движения.

Материальная точка — это модель реальных объектов, реальных тел. Считая тело материальной точкой, мы отвлекаемся от несущественных для решения конкретной задачи признаков, в частности, от размеров тела.

5. При перемещении тело последовательно проходит точки пространства, соединив которые, можно получить линию. Эта линия, вдоль которой движется тело, называется траекторией. Траектория может быть видимой или невидимой. Видимую траекторию описывают трамвай при движении по рельсам, лыжник, скользя по лыжне, мел, которым пишут на доске. Траектория летящего самолёта в большинстве случаев невидима, невидимой является траектория ползущего насекомого.

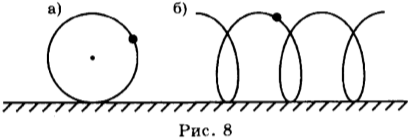
Траектория движения тела относительна: её форма зависит от выбора системы отсчёта. Так, траекторией точек обода колеса велосипеда, движущегося по прямой дороге, относительно оси колеса является окружность, а относительно Земли — винтовая линия (рис. 8 а, б).

6. Одной из характеристик механического движения является путь, пройденный телом. Путём называют физическую величину, равную расстоянию, пройденному телом вдоль траектории.

Если известны траектория тела, его начальное положение и пройденный им путь за время ​ \( t \) ​, то можно найти положение тела в момент времени ​ \( t \) ​. (рис. 9)

Путь обозначают буквой ​ \( l \) ​ (иногда ​ \( s \) ​), основная единица пути 1 м: \( [\,\mathrm\,] \) = 1 м. Кратная единица пути — километр (1 км = 1000 м); дольные единицы — дециметр (1 дм = 0,1 м), сантиметр (1 см = 0,01 м) и миллиметр (1 мм = 0,001 м).

Путь — величина относительная, значение пути зависит от выбора системы отсчёта. Так, путь пассажира, переходящего из конца движущегося автобуса к его передней двери, равен длине автобуса в системе отсчёта, связанной с автобусом. В системе отсчёта, связанной с Землёй, он равен сумме длины автобуса и пути, который проехал автобус относительно Земли.

7. Если траектория движения тела неизвестна, то значение пути не позволит установить его положение в любой момент времени, поскольку направление движения тела не определено. В этом случае используют другую характеристику механического движения — перемещение.

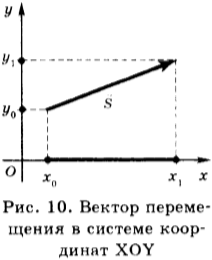
Перемещение — вектор, соединяющий начальное положение тела с его конечным положением (рис. 10)

Перемещение — векторная физическая величина, имеет направление и числовое значение, обозначается ​ \( \overrightarrow \) ​. Единица перемещения \( [\,\mathrm\,] \) = 1 м.

Зная начальное положение тела, его перемещение (направление и модуль) за некоторый промежуток времени, можно определить положение тела в конце этого промежутка времени.

Следует иметь в виду, что перемещение в общем случае не совпадает с траекторией, а модуль перемещения — с пройденным путём. Это совпадение имеет место лишь при движении тела по прямолинейной траектории в одну сторону. Например, если пловец проплыл 100-метровую дистанцию в бассейне, длина дорожки которого 50 м, то его путь равен 100 м, а модуль перемещения равен нулю.

Перемещение, так же как и путь, величина относительная, зависит от выбора системы отсчёта.

При решении задач пользуются проекциями вектора перемещения. На рисунке 10 изображены система координат и вектор перемещения в этой системе координат.

Модуль вектора перемещения равен: ​ \( s=\sqrt \) ​.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. В состав системы отсчёта входят

1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы

2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно

1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора

4. Относительно какого тела покоится автомобиль, движущийся по автостраде?

1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода

5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?

6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?

7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?

1) прямая
2) окружность
3) дуга
4) винтовая линия

8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь ​ \( l \) ​ и модуль перемещения ​ \( s \) ​ мяча за всё время движения?

1) \( l \) = 3,3 м, ​ \( s \) ​ = 3,3 м
2) \( l \) = 3,3 м, \( s \) = 0,7 м
3) \( l \) = 0,7 м, \( s \) = 0,7 м
4) \( l \) = 0,7 м, \( s \) = 3,3 м

9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?

1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй

10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса ​ \( R \) ​. Чему равны при этом путь ​ \( l \) ​ и модуль перемещения ​ \( s \) ​ точки обода?

11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.

ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор

ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта

12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.

ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения

ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная

Часть 2

13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.

Источник

Что такое перемещение материальной точки

Рис. 1.2.1. Траектория и перемещение материальной точки

Рис. 1.2.2. Векторы перемещения материальной точки:
а) неэквивалентность результата перемещения при одинаковой длине вектора;
б) сложение векторов

Очевидно, что, хотя величины перемещений одинаковы, результат далеко не равноценен, поскольку МТ оказывается в разных пространственных положениях. Если МТ совершает сложное движение, которое можно описать, например, двумя последовательными перемещениями

Квадрат модуля вектора (1.2.1) в общем случае можно вычислить, используя теорему косинусов:

К числу векторных величин в механике относят скорость, ускорение, силу и ряд других. Длина отрезка в установленном масштабе имеет смысл модуля вектора, стрелкой показывают направление вектора.

Величины, для определения которых достаточно знать одно число, называются скалярными ( скалярами ). Скалярами являются путь, время, масса, температура и другие.

Рис. 1.2.3. Радиус-вектор материальной точки в зависимости от времени

По определению, соотношение (1.2.4) представляет собой производную по времени:

и называется истинной или мгновенной скоростью МТ. Из Рис. 1.2.4 ясно, что вектор является секущей траектории движущейся МТ.

Рис. 1.2.4. Скорость как секущая траектории материальной точки

1.2.2. Вычисление пройденного пути

Из соотношения (1.2.6) следует, что при малых Δt приближенно выполняется:

Используя (1.2.7), можно приближенно представить:

Подставляя (1.2.9) в (1.2.8), получим:

В пределе при стремлении к нулю всех промежутков Δt i сумма, стоящая в правой части (1.2.10), будет точно равна пути:

Скорость есть функция времени v = v(t). В математическом анализе в общем виде для произвольной функции f(x) задают определенный интеграл следующим образом:

Рис. 1.2.5. Геометрическая интерпретация пути

Движение, при котором скорость, изменяясь как угодно по направлению, не меняется по величине, называют равномерным. Тогда все значения v i в формуле (1.2.11) будут одинаковыми, и общий множитель можно вынести за знак суммы, при этом сумма временных промежутков равна времени t. В результате приходим к простому соотношению:

Из (1.2.14) следует, что при равномерном движении скорость равна пути, деленному на время:

1.2.3. Ускорение

Если ускорение постоянно (движение МТ равноускореннное ), то из (1.2.17) следует:

1.2.4. Нормальное и тангенциальное ускорение

Рассмотрим равномерное движение МТ по окружности. Пусть в рассматриваемый момент времени t МТ находится в положении 1 (Рис. 1.2.6).

Рис. 1.2.6. Равномерное движение по окружности радиуса R

Подставляя (1.2.21) в (1.2.23), имеем:

Разделив обе части (1.2.24) на Δt и переходя к пределу, получим ускорение:

Рис. 1.2.7. К определению полного ускорения

Эти составляющие выберем так, чтобы расстояние от точки 1 до конца вектора было равно модулю скорости в начальный момент времени. Тогда, очевидно, модуль вектора будет равен приращению модуля скорости:

Для вектора полного ускорения запишем:

Тангенциальное ускорение, учитывая (1.2.29), имеет явный вид:

Тогда из (1.2.29), (1.2.31) и (1.2.32) следует:

Итак, вектор полного ускорения равен векторной сумме тангенциального и нормального ускорения, первый из которых ( ) направлен по касательной к траектории, а второй ( ) перпендикулярен к вектору скорости и направлен к центру кривизны траектории (Рис. 1.2.8).

Рис. 1.2.8. Вектор полного ускорения материальной точки

1.2.5. Кинематика вращательного движения.
Угловые скорости и ускорение

Все точки абсолютно твердого тела, вращающегося вокруг некоторой оси ОО, движутся по окружностям, центры которых лежат на оси вращения. Радиус-вектор каждой точки за время Δt поворачивается на один и тот же угол Δφ. Поворот тела на некоторый угол φ можно задать в виде отрезка, длина которого равна j, а направление совпадает с осью, вокруг которой совершен поворот. Для того чтобы указать, в какую сторону совершается поворот вокруг данной оси, условились связывать направление поворота и изображающего его отрезка так называемым правилом правого винта. Согласно этому правилу, направление отрезка должно быть таким, чтобы, глядя вдоль этого направления, мы видели поворот совершающимся по часовой стрелке (так, как происходит при вращении винта с правой нарезкой резьбы). Векторы, направление которых связывается с направлением вращения, называют аксиальными (в отличие от векторов перемещения, скорости, ускорения, относящихся к полярным векторам).

является модулем угловой скорости тела. Вектор угловой скорости направлен вдоль оси, вокруг которой вращается тело, в сторону, которая определяется правилом правого винта (Рис. 1.2.9).

Число оборотов в единицу времени (частота вращения) равно:

Точка, находящаяся на расстоянии R от оси вращения, проходит при этом путь Δs, равный

По определению, линейная скорость МТ равна:

Следовательно, взаимосвязь между угловой скоростью вращения тела ω и линейной скоростью МТ имеет вид:

Итак, чем дальше отстоит точка от оси вращения, тем с большей линейной скоростью она движется.

Найдем линейное ускорение точек вращающегося тела. Подставляя в выражение для модуля нормального ускорения (1.2.27) линейную скорость (1.2.44), получим:

Используя выражение для модуля тангенциального ускорения (1.2.33) и (1.2.44), имеем:

Следовательно, между тангенциальным и угловым ускорением есть взаимосвязь:

Таким образом, как нормальное, так и тангенциальное ускорение растет линейно с увеличением расстояния от МТ до оси вращения тела.

Найдем взаимосвязь между векторами и с помощью векторного произведения. Пусть тело вращается вокруг оси z с угловой скоростью (Рис. 1.2.11).

Рис. 1.2.11. Связь между векторами угловой и линейной скорости

© ФГОУ ВПО Красноярский государственный аграрный университет, 2013

Источник

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Ноябрь 1969 г. И. Савельев

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Источник

Механическое движение и его характеристики

теория по физике 🧲 кинематика

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

По характеру движения точек тела выделяют три вида механического движения:

По типу линии, вдоль которой движется тело, выделяют два вида движения:

По скорости выделяют два вида движения:

По ускорению выделяют три вида движения:

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

Способы описания механического движения

Описать механическое движение можно двумя способами:

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

Перемещение

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет вид:

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

Точка В имеет координаты (5; 10).

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид :

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник