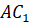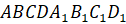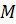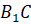Что такое параллельное проектирование
Реферат по математике на тему «Параллельное проектирование»
тема: Параллельное проектирование
1 Определение и свойства параллельного проектирования
2 Примеры изображений пространственных фигур на плоскости
3 РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ ПАРАЛЛЕЛЬНОГО ПРЕКТИРОВАНИЯ
4 Использование свойств параллельного проектирования в живописи
Исследование и применение свойств параллельного проектирования при изображении фигур на плоскости и при построении сечений многогранников.
Научиться быстро и точно производить различные построения
В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно в геометрии для этого используется параллельное проектирование.

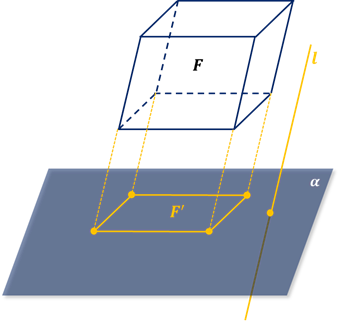
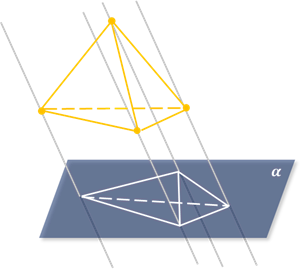
Параллельное проектирование позволяет получать наглядные изображения пространственных (трёхмерных) фигур на (двумерной) плоскости (рис. 4). Дело в том, что параллельное проектирование сохраняет ряд важных черт изображаемой фигуры. Перечислим основные свойства параллельного проектирования в предложении, что направление проектирования не параллельно рассматриваемым прямым и отрезкам (в противном случае их проекциями являются точки.
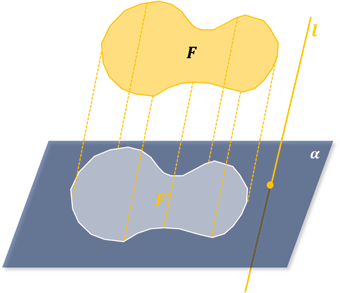
Задача в следующем: есть пространственная фигура, нужно изобразить ее на плоскости (на листе бумаги). Самым простым способом (но не единственным) является параллельное проектирование.
Его идея состоит в том, чтобы все точки фигуры переносить параллельно в одну сторону до тех пор, пока они не попадут на плоскость изображения (см. рис. 26). Пример параллельного проектирования – тень на стене от предмета, освещенного солнечными лучами (см. рис. 27).

Определение. Проектирование в направлении прямой, перпендикулярной плоскости проекций, называется ортогональным .
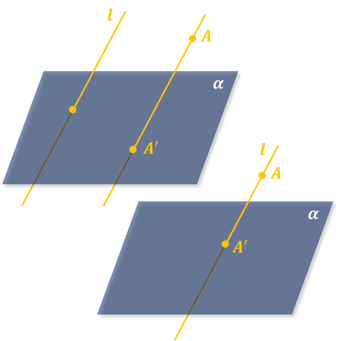
1. Все точки проектирующей прямой проектируются в одну точку — точку пересечения этой прямой с плоскостью проекций
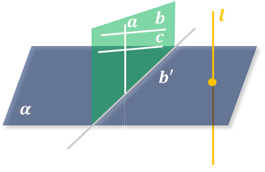
2. Проекция прямой есть прямая. Действительно, все прямые, проектирующие точки данной прямой m ′ (рис. 76)

3. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую (рис. 77)
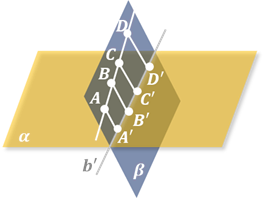
4. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой. Отношение длин отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин проекций этих отрезков. рис. 78


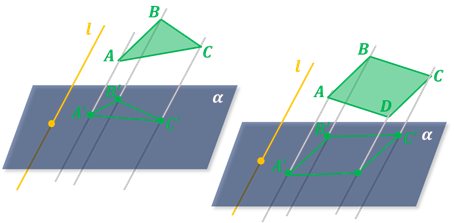
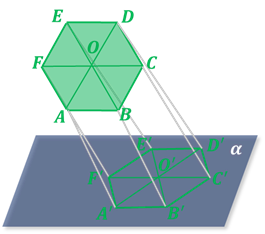
Рассмотрим теперь параллельную проекцию правильного шестиугольника ABCDEF с центром в точке O (рис. 7). Выберем какой-нибудь треугольник, например, AOB. Его проекцией может быть треугольник A’O’B’ на плоскости p (рис. 8), имеющий произвольную форму. Шестиугольник A’B’C’D’E’F’ и будет искомой проекцией правильного шестиугольника ABCDEF .
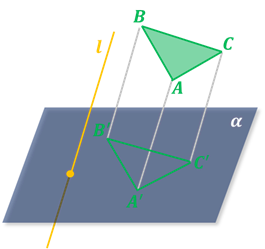
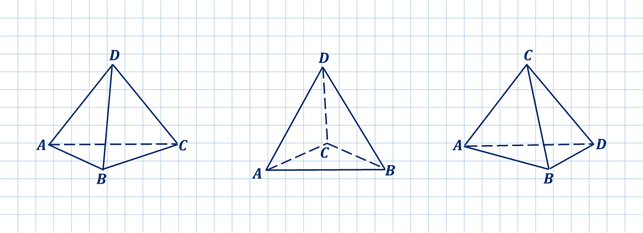
При изображении пространственных фигур пользуются тем фактом, что фигуру, состоящую из сторон и диагоналей любого выпуклого или невыпуклого четырёхугольника, можно считать изображением треугольной пирамиды при определённом выборе направления проектирования и плоскости, на которую проектируется эта пирамида.
Например, фигуры, изображённые на экране, являются изображениями треугольной пирамиды при соответствующем выборе направления проектирования.
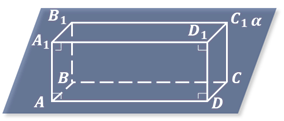
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами (рис. 11)

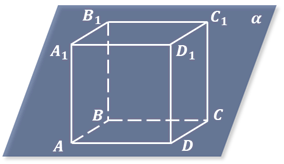
При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами
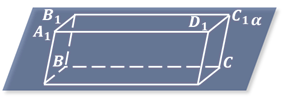
Аналогичным образом изображается прямоугольный параллелепипед.
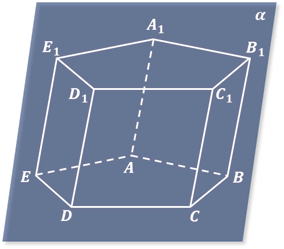
Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий её основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.

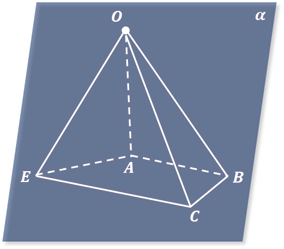
Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить её с вершинами многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.
Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.

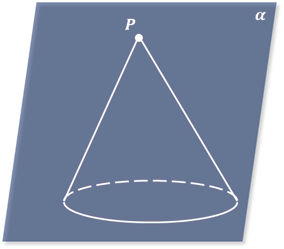
Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через неё две образующие, являющиеся касательными к этому эллипсу.
Точки 












. На диагонали 






. Дан треугольник АВС площадью S. Точки M и N – середины его сторон АС и АВ соответственно. Точки Р и Q делят сторону ВС на три равных отрезка так, что BP = PQ = QС. Найти площадь общей части четырёхугольника ANPQ и треугольника ВМС.
Площади треугольников с общим углом относятся друг к другу как произведения сторон, содержащих общий угол. 3) Пусть сторона треугольника А1В1С1 равна 6х, тогда N1B1=3x, а В1P1=2x В1E1- биссектриса треугольника N1B1P1. Как площади треугольников, одна из сторон которых лежит на одной прямой и имеющие общую высоту, проведенную к этой прямой. Откуда 4) Площади треугольников с общим углом относятся друг к другу как произведения сторон, содержащих общий угол. Т. Е
Найти площадь общей части четырёхугольника ANPQ и треугольника ВМС. Дано: ВP:PQ:QC=1:1:1, М-середина AC, N-середина AВ, Площадь = S, Найти площадь ЕPQ
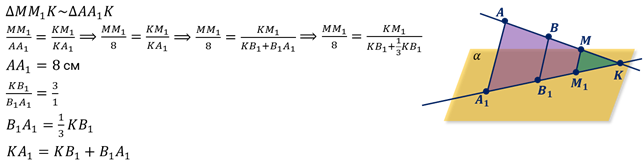
Задача №4. (проектирование на прямую) На сторонах треугольника АВ и АС треугольника АВС взяты точки М и N соответственно, а отрезки ВN и СМ пересекаются в точке К. Найти ВК: NK, если АN : NC = 2 : 3 и СK : KM = 5:2.
Ответ: ВК : КN = 5 : 2
4 Использование свойств параллельного проектирования в живописи
1 При параллельном проектировании отрезки параллельных прямых изображаются отрезками параллельных прямых или отрезками одной прямой,
2 В задачах на построение сечений не принято проводить исследования, хотя было бы очень полезно его провести
3 Проведя исследование построения сечения методом следов, я установил, что метод следов легко объясним, нагляден, но не всегда удобен в практике построения сечений многогранников,
4 Изучив параллельное проецирование, научились легко и быстро производить различные построения на плоскости. Эти навыки и умения помогли мне при изучении предметов школьного курса, таких как геометрия и черчение,
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Что такое параллельное проектирование
Таким образом, проекция окружности получается сжатием или растяжением окружности в направлении какого-нибудь ее диаметра в одно и то же число раз. Такая фигура на плоскости называется эллипсом. Например, на рисунке 10 изображен эллипс, полученный из окружности сжатием в направлении диаметра CD в два раза.
Приведем примеры изображений пространственных фигур на плоскости.
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами (рис. 11).
При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами (рис. 12). Аналогичным образом изображается прямоугольный параллелепипед (рис. 13).
Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий ее основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы (рис. 14).
Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий ее основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить ее с вершинами многоугольника (рис. 15). Полученные отрезки будут изображать боковые ребра пирамиды.
Современный шведский архитектор О. Рутерсвард посвятил невозможным объектам серию своих художественных работ. Некоторые из них представлены на рисунке 21.
Параллельное проектирование. Изображение пространственных фигур
Урок 33. Подготовка к ЕГЭ по математике
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Параллельное проектирование. Изображение пространственных фигур»
В стереометрии большое значение имеет умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости пространственные фигуры.
Итак, зачастую для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование. Определяется оно следующим образом.
Пусть 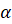
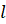
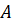
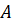
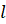
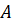
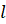
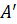
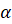
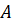
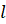
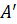
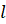
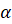
Точка 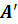
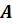
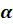
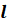
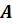
Плоскость 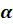
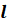
Все прямые, параллельные прямой 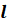
Пусть 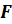
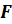
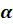
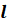
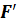
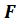
Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.
Вспомним основные свойства параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования.
1. Проекция прямой есть прямая, а проекция отрезка — отрезок.
2. Проекции параллельных прямых параллельны или совпадают.
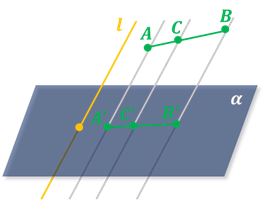
3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
Следствие. При параллельном проектировании середина отрезка проектируется в середину его проекции.
При параллельном проектировании могут искажаться размеры отрезков и углы, но обязательно сохраняется параллельность прямых.
Если точка делит отрезок в отношении 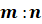
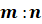
Центр правильного треугольника отображается в точку пересечения медиан проекции этого треугольника, центр квадрата — в точку пересечения диагоналей проекции квадрата.
А теперь давайте поговорим об изображении пространственных фигур.
Рассмотренные свойства параллельного проектирования применяются при выполнении рисунков (изображений фигур), иллюстрирующих теоремы и задачи стереометрии.
Изображением фигуры 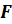
Выполняя изображения фигур, расположенных в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном проектировании, а в остальном изображение может быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были наглядными и давали верное представление о них.
При различном выборе плоскости проекций и направления проектирования получаются различные проекции данной фигуры, а значит, и различные её изображения.
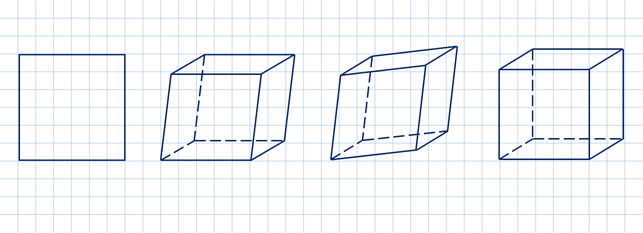
Например, вы видите фигуры, которые являются изображениями куба.
Причём изображение куба, данное на первом рисунке, не даёт представления о кубе, наглядным является изображение, которое дано на последнем рисунке.
При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования.
Итак, проекцией треугольника может быть любой треугольник.
При этом величины углов и отношение длин непараллельных сторон не сохраняются, но при этом медианы треугольника отображаются в медианы его проекции. В частности, за изображение прямоугольного, равнобедренного, равностороннего треугольников можно принять любой треугольник.
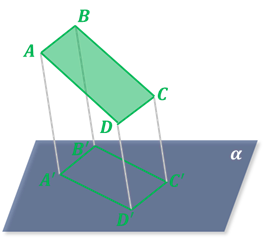
Параллелограмм проектируется в параллелограмм, так как параллельные прямые сохраняют параллельность.
В частном случае за изображение прямоугольника, квадрата, ромба можно принять любой параллелограмм.
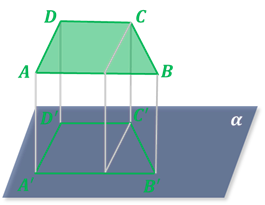
Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований.
Правильный шестиугольник проектируется в искажённый шестиугольник с сохранением параллельности противолежащих сторон.
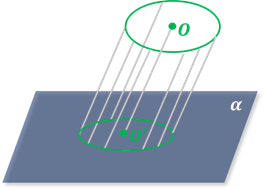
Окружность проектируется в эллипс, большая ось которого имеет длину, равную диаметру окружности.
При изображении пространственных фигур пользуются тем фактом, что фигуру, состоящую из сторон и диагоналей любого выпуклого или невыпуклого четырёхугольника, можно считать изображением треугольной пирамиды при определённом выборе направления проектирования и плоскости, на которую проектируется эта пирамида.
Например, фигуры, изображённые на экране, являются изображениями треугольной пирамиды при соответствующем выборе направления проектирования.
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.
При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.
Аналогичным образом изображается прямоугольный параллелепипед.
Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий её основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.
Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить её с вершинами многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.
Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.
Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через неё две образующие, являющиеся касательными к этому эллипсу.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Точки 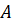
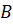
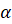
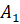
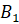
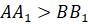
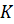
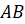
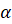
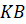
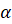
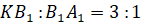
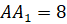
Задача вторая. На диагонали