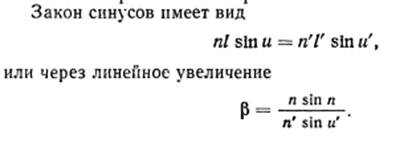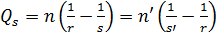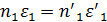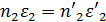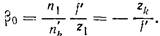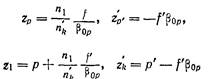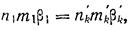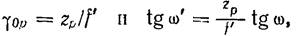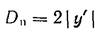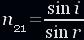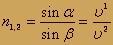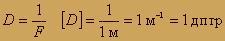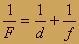Что такое параксиальная область
Параксиальная оптика — Понятие параксиальная область
Как уже говорилось выше, параксиальная оптика неразрывно связана с параксиальной областью. Необходимо конкретизировать понятие «параксиальная область». Утверждение, что это область бесконечно приближенная к оптической оси несколько размыто. Хотелось бы максимально точно определить «размеры» параксиальной области. Для этого вначале необходимо ближе ознакомится с самой распространенной формой поверхности, разделяющей области с различными коэффициентами преломления.
Итак, знакомьтесь – сфера. Я думаю, для многих читателей не секрет, что подавляющее число линз являются сферическими (сферическая линза). Дам свое (не оптическое) определение сферической линзы:
Двояковыпуклая сферическая линза – кусок стекла, ограниченный двумя сферами.
Приведу пример построения положительной двояковыпуклой линзы. Изначально у нас есть прямоугольный параллелепипед стекла подходящего размера (рисунок 1).
Рисунок 1. Стеклянная заготовка.
У нашей линзы должно быть две (как минимум одна) выпуклых сферических поверхности. Ограничим нашу стеклянную заготовку сферой с одной стороны (рисунок 2).
Рисунок 2. Стеклянная заготовка ограниченная одной сферой.
Затем сделаем то же самое с другой стороной заготовки (рисунок 3).
Рисунок 3. Стеклянная заготовка ограниченная двумя сферами.
Обрежем все лишнее – удалим «куски стекла» не вошедшие в область пересечения двух сфер (рисунок 4).
Рисунок 4. Линза ограниченная двумя сферами.
В итоге мы получим желаемую двояковыпуклую линзу со сферическими поверхностями (рисунок 5).
Рисунок 5. Двояковыпуклая линза со сферическими поверхностями.
Так какая же связь между этой линзой и параксиальной областью? Для ответа на этот вопрос придется рассмотреть несколько формул.
Сферическая поверхность, центр которой находится в начале координат, задается следующей формулой:
Нам же необходимо рассмотреть случай, когда центр сферической поверхности находится на оптической оси (ось 
Для того чтобы не таскать за собой лишние переменные несколько упростим формулу (2) заменив 

После такой подстановки будем иметь:
Раскроем скобки и упростим выражение до следующего вида:
Решим квадратное уравнение относительно 
Этому решению соответствует рисунок 6.
Нас интересует только первая точка пересечения. Решением для этой точки является выражение (5) со знаком минус:

Вынесем R за скобки:
Заменим радиус сферы R на кривизну определяемую следующим выражением:
В результате получим:
Применим несколько простых математических преобразований. Честно говоря, я сомневался, стоит ли их тут приводить. Может, хватило бы конечного результата? Но все-таки решил немного облегчить Вам жизнь и расписал:
Таким образом, решение для z выглядит так:
Выражение (11) описывает сферу заданного радиуса. Но для определения параксиальной области нам нужно рассмотреть выражение (9). А если точнее, то его сначала следует привести к такому виду:
А затем разложить корень в правой части равенства в степенной ряд:
И, наконец, выражение для z:
А вот отсюда уже следует вывод:
Параксиальная область – область, в которой любая отражающая или преломляющая поверхность может быть описана первым членом степенного ряда (14).
Это значит, что для определения z в параксиальной области для расчета будет использоваться следующая формула:
Кроме того, нужно отметить, что мы будем ограничивать протяженность поверхностей объекта или изображения слагаемыми, которые пропорциональны квадрату величины объекта или изображения. Вдобавок, мы будем полагать, что любые углы, которые мы будем встречать при расчете, настолько малы, что их значение в градусах будет равно их же значению в радианах. Если принимать во внимание эти условия, то можно показать, что в параксиальной области любая поверхность находящееся в пространстве предметов идеально отображается в пространстве изображений.
Параксиальная область лучей
Условие синуса
Параксиальная область лучей
Лучи, образующие малые углы 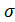
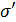
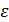
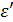
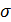
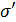
Формулы 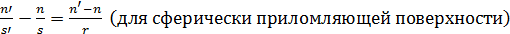
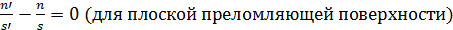
Таким образом, для параксиальной области имеем 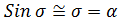
Инварианты
Сгруппировав в ( 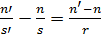
Инвариант 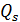
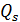
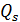
Оптический инвариант или закон преломления ( 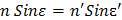
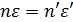
Напишем (1) для двух поверхностей:
Величины 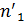
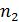
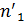
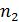
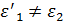
Принимая 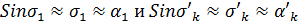
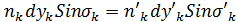
ца в параксиальной области для системы: 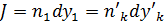
Инвариант (2) является полным инвариантом; он показывает, что отрезок прямой или часть площадки, перпендикулярных к оптической оси, при прохождении лучей через систему преломляющих поверхностей, может изображаться в виде совершенного (идеального) отрезка ила плошадки.
15.Сфери́ческая аберра́ция — аберрация оптических систем; нарушение гомоцентричности пучков лучей от точечного источника, прошедших через оптическую систему без нарушения симметрии строения этих пучков. Сферическую аберрацию принято рассматривать для пучка лучей, выходящего из точки предмета, расположенной на оптической оси. Однако, сферическая аберрация имеет место и для других пучков лучей, выходящих из точек предмета, удаленных от оптической оси, но в таких случаях она рассматривается как составная часть аберраций всего наклонного пучка лучей. Ко́ма проявляется в том, что каждый участок оптической системы, удалённый от её оси на расстояние d (кольцевая зона), даёт изображение светящейся точки в виде кольца, радиус которого тем больше, чем больше d; может рассматриваться каксферическая аберрация лучей, проходящих не через оптическую ось системы. Центры колец не совпадают, в результате чего их наложение, то есть изображение точки, даваемое системой в целом, принимает вид несимметричного пятна рассеяния. Кома очень велика в параболических рефлекторах и является основным фактором, ограничивающим их поле зрения. В сложных оптических системах кому обычно исправляют совместно со сферической аберрацией подбором линз. Астигмати́зм — аберрация, при которой изображение точки, находящейся вне оси, и образуемое узким пучком лучей, представляет собой два отрезка прямой, расположенных перпендикулярно друг другу на разных расстояниях от плоскости безаберрационного фокуса. Астигматизм возникает вследствие того, что лучи наклонного пучка имеют различные точки сходимости — точки меридионального или сагиттального фокусов бесконечно тонкого наклонного пучка.Кривизна́ по́ля изображе́ния — аберрация, в результате которой изображение плоского объекта, перпендикулярного коптической оси объектива, лежит на поверхности, вогнутой либо выпуклой к объективу. Эта аберрация вызывает неравномерную резкость по полю изображения. Поэтому, когда центральная часть изображения фокусирована резко, то его края будут лежать не в фокусе и изобразятся нерезко. Если установку на резкость производить по краям изображения, то его центральная часть будет нерезкой. Кривизна поля изображения исправляется подбором кривизны поверхностей линз, их толщины и расстояний между ними. Достигает больши́х величин у простых не длиннофокусных объективов и существенно уменьшена у более сложных. Для её хорошего исправления, с учетом других аберраций, обычно необходимо, чтобы объектив содержал не менее двух отрицательных линз. Дисторсия — аберрация оптических систем, при которой линейное увеличение изменяется по полю зрения. При этом нарушается подобие между объектом и его изображением. Исправляется подбором линз и других элементов оптической системы при её разработке. Если присутствует в цифровом изображении, может быть исправлена программно.
16. Отдельные части реальной оптической системы, например, линзы, зеркала и призмы, всегда имеют определенные поперечные размеры, которые ограничивают ширину пучков лучей, проходящих через оптическую систему. Кроме того, в оптических системах приходится ставить специальные преграды в виде светонепроницаемых деталей с отверстиями, центрированными относительно оптической оси. Все части оптической системы (специальные преграды, оправы линз и других деталей), ограничивающие размеры пучков лучей, проходящих через оптическую систему, называются диафрагмами. Диафрагмы могут быть круглыми, полукруглыми, квадратными, прямоугольными и т, д. Форма диафрагмы зависит от назначения системы. В большинстве случаев они имеют круглую форму. Диафрагмы круглой формы в некоторых системах имеют переменный диаметр (в фотообъективах). Диафрагмы, устанавливаемые в оптических системах, предназначаются для:1) ограничения пучков лучей, выходящих из точек предмета, расположенной на оптической оси;2) ограничения пучков лучей, выходящих из точек предмета, расположенных вне оптической оси;3) ограничения изображаемого оптической системой пространства;4) уменьшения количества вредного (рассеянного) света;5) специальных целей. Ограничение пучков лучей, проходящих через оптическую систему, имеет важные последствия не только геометрического, но и физического характера:
1. Диафрагмы определяют количество световой энергии, проходящей через систему.
2. Ограничение пучков лучей вызывает дифракцию, которая определяет предел разрешения оптической системы, т. е. тот предел, когда близко расположенные точки предметной плоскости изображаются раздельно. Если оптическая система работает совместно с глазом, то его ‘зрачок играет роль одной из диафрагм, положение и размер которой следует принимать во внимание. При рассмотрении ограничения пучков лучей в оптических системах считают, что эти системы являются идеальными.
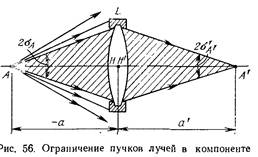
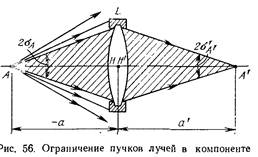
Диафрагма, ограничивающая пучок лучей, выходящих из осевой точки предмета, называется апертурной диафрагмой. (На рис. 56 апертурной диафрагмой является оправа компонента). Из осевой точки предмета через компонент пройдет пучок лучей, заключенных в конусе, основанием которого является диаметр оправы компонента, а вершиной точка А. Оправа компонента, являющаяся диафрагмой, ограничивает, как падающий на компонент, так и выходящий из него пучок лучей. Плоский угол раскрытия пучка в пространстве предметов составляет 2ол = £VV а в пространстве изображений 2з’д, = — DaIu’, где DA—диаметр оправы компонента.
Диафрагма, расположенная в плоскости предмета или в одной из плоскостей, с ней сопряженных, и ограничивающая размер линейного поля оптической системы в пространстве изображении, называется полевой диафрагмой.
Любая диафрагма, кроме апертурной и полевой, которая ограничивает пучки лучей, выходящих нз точек предмета, лежащих вне оптической оси, называется виньетирующей
17. Параксиальное изображение апертурной диафрагмы в пространстве предметов, или апертурная диафрагма, расположения в пространстве предметов, называется входным зрачом системы. Параксиальное изображение апертурной диафрагмы в пространстве изображений, или апертурная диафрагма, расположенная в пространстве изображений, называется выходным рачком системы. В соответствии с этими определениями на рис. 56 апертурной диафрагмой, входным и выходным зрачками является диаметр опэавы компонента.
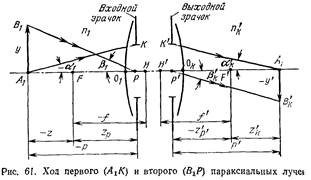
Найдем формулу Гаусса для зрачков, т. е. для отрезков р и р’, определяющих положения зрачков относительно предмета и изображения (рис. 61). Линсйноэ увеличение в сопряженных точках Л\ и Лк равно
Положение сопряженных точек Р. и Р’ относительно фокусов F и F’ системы 0\Ок определяется координатами z,; и z’p>, поэтому для линейного увеличения в зрачках можем написать
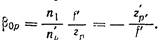
для zp и z’p’ имеем
после преобразования получил 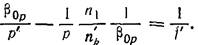
п,ц и рол. = 1. Тогда 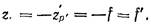
где Ш\ и trik—выготы пересечения первого параксиального луча плоскостями входного и выходного зрачков.
18. Любая оптическая система отображает определенную часть пространства, расположенного вокруг оптической оси, которое называется полем системы. Ограничение поля оптической системы производится с помощью специальных диафрагм.
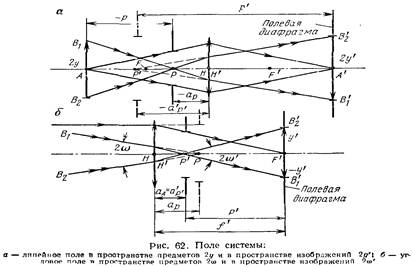
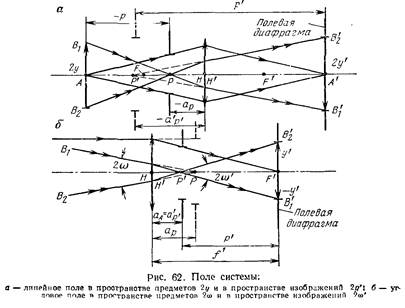
расположенной на конечном расстоянии, называется линейным полем оптической системы в пространстве предметов 2 у (рис. 62, а). Наибольший размер изображения, лежащего на конечном
расстоянии, называется линейным полем оптической системы в пространстве изображений 2 //’.
Если полевая диафрагма расположена в члоекг.сти предмета, то ее размеры определяют линейное поле в пространстве предметов, а если она расположена в плоскости изображения, го линейное поле в iipocipiiHCTBe изображений. Связь между линейньгми полями системы осуществляется через линейное увеличение. Угловым полем оптической системы в пространстве предметов называется абсолютное значение удвоенного угла между оптической осью и лучом в пространстве предметов, проходящего через центр входного зрачка (центр апертурной диафрагмы) и край полевой диафрагмы. Угловым полем оптической системы в пространстве изображений называется абсолютное значение удвоенного угла между оптической осью и лучом в пространстве изображений, проходящим через центр выходного зрачка (центр апертурной диафрагмы) и край полевой диафрагмы. Угловое поле обозначается: в пространстве предметов — 2w; в пространстве изображений— 2а/. Так как лучи, проходящие через края предмета и изображения и центры зрачков, являются главными лучами, то угловое поле 2w представляет собой угол между главными
лучами в пространстве предметов, а угловое поле 2а/ — угол между главными лучами в пространстве изображений. Связь между углами 2w и 2о/ характеризуется угловым увеличением в
зрачках 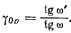
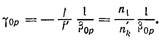
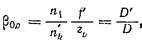
Диаметр полевой диафрагмы
Определение положения и диаметра полевой диафрагмы производится одновременно с определением положения и диаметров входного и выходного зрачков системы. Для этого рассчитывается ход апертурного и главного лучей. Ход апертуриого луча определяют диаметры зрачков и положение апертурной диафрагмы, а ход главного луча—положение зрачков и диаметр полевой диафрагмы.
19. Наибольший размер изображаемой части плоскости предмета расположенный на конечном расстоянии, наз. Линейным полем оптической системы в пространстве предметов 2y. Наибольший размер изображения, лежащего на конечном расстоянии, наз. Линейным полем оптической системы в пространстве изображений 2y’.
Угловым полем оптической системы в пространстве предметов наз. абсолютное значение удвоенного угла между оптической осью и лучом в пространстве предметов, проходящего через центр входного зрачка и край полевой диафрагмы. Угловым полем оптической системы в пространстве изображений наз. абсолютное значение удвоенного угла между оптической осью и лучом в пространстве изображений, проходящего через центр входного зрачка и край полевой диафрагмы.
Полевая диафрагма— диафрагма, расположенная в плоскости предмета или в одной из плоскостей, с ней сопряженных, и ограничивающая размер линейного поля оптической системы в пространстве изображений.
Диаметр полевой диафрагмы: Dn=2|y ‘ |. Ф-ла справедлива для любой системы независимо от положения входного зрачка.
Определение положения и диаметра полевой диафрагмы производится одновременно с определение положения и диаметров входного и выходного зрачков системы. Для этого рассчитывается ход апертурного и главного лучей. Ход апертурного луча определяют диаметры зрачков и положение апертурной диафрагмы, а ход главного луча-положение зрачков и диаметр полевой диафрагмы.
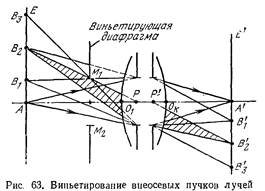
Виньетирование-явление частичного срезания внеосевых пучков лучей. В результате виньетирования происходит ослабление освещенности изображения от центра к краю.
Виньетирующая диафрагма – диафрагма, кроме апертурной и полевой, которая ограничивает пучки лучей, выходящих из точек предмета, лежащих вне оптической оси.
Выходным окном – наз. параксиальное изображение виньетирующей диафрагмы в пространстве изображений или сама виньетирующая диафрагма, расположенная в пространстве изображений. Из этих определений вытекает что входное и выходное окна сопряжены друг с другом относительно всей системы, если она состоит из нескольких частей. Для оценки виньетирования вводятся клэф-ты: 1.Линейное виньетирование Kω=2mb/2h, 2mb –ширина наклонного пучка лучей в меридиальной плоскости, 2h-ширина осевого пучка лучей в том же сечении. 2. Коэф-т геометрического виньетирования KA=Aω/Ap, Aω-площадь сечения наклонного пучка лучей, перпендик-го к оптической оси, Ap-площадь осевого пучка лучей в том же сечении.
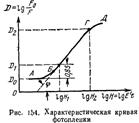
20. Основные характеристики фотообъективов:
1. Фокусное расстояние определяет масштаб изображения на снимке, которое определяется линейным увеличением. β0=y’/y=-f/z, z’=f ‘ 2 /z=f ‘ 2 (α-f).
3. Физическая светосила объектива (D/f ‘) 2 τ=(1/Kф) 2
4. Поле фотообъектива определяется той частью плоскости изображения, в которой находится изображение удовлетворительного качества. Поле указывается либо размерами сторон кино или фотокадра, либо в угловой мере.
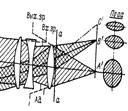
21. Лупа-самый простой оптический прибор. Обычно либо положительная линза или система линз, предназначенная для наблюдения предмета расположенной либо в передней фокальной плоскости, либо вблизи неё.
Основными оптическими характеристиками лупы являются:1. Гл-видимое увеличение Гл=tgω’/tgω, ω-угол под которым виден предмет без лупы, ω’— угол под которым рассматривается изображение после лупы.
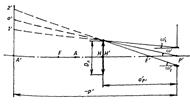
Телескопическая лупа. Представляет собой зрительную трубу с насадкой. Предмет располагают в передней фокальной плоскости насадки, после насадки формируется паралл-й пучок лучей, поступающий в зрительную трубу. Увеличение телескопической лупы: Гл=βн.об Гок, βн.об-линейное увеличение системы «насадка+объектив зрительной трубы», Гок— видимое увеличение окуляра.
Бинокулярные призматические лупы. В этих лупах оптическая ось насадки составляет небольшой угол α с осью лупы. Характеристики: видимое увеличение Гл=ГнГт, Гн— окулярное увеличение насадки, Гт— видимое увеличение зрительной трубы.
Диаметр полевой диафрагмы. Dпт=2y‘.
Микроскопприменяют для большого увеличения.
Видимое увеличение микроскопа- Гм=βоб Гок, βоб— линейное увеличение объектива, Гок— видимое увеличение окуляра.
Диаметр выходного зрачка D’
Нормальное увеличение микроскопа – увеличение при котором субъективная яркость изображения будет максимальной.
Полезное увеличение микроскопа – увеличение при котором глаз полностью использует разрешающую способность микроскопа.
22. Зрение — способность видеть — дает человеку возможность познавать окружающий нас мир и осуществляется посредством сложной оптической и физиологической системы — глаза. С помощью глаза человек получает более 80% всей информации. Глаз — прибор весьма чувствительный; диапазон изменения яркостей, воспринимаемых глазом, составляет 1012. Глаз
различает до 25 тысяч оттенков в солнечном свете и может воспринять вспышку света длительностью менее миллисекунды. Глаз человека часто действует вместе с оптическими
инструментами, поэтому при разработке наиболее оптимальных конструкций оптических приборов необходимо учитывать оптические и физиологические свойства глаза.
Глаз представляет собой центрированную оптическую систем?, состоящую из двух линз: роговицы и хрусталика, между которым> находится передняя камера, заполненная водянистой влагой. Пе
редняя поверхность роговицы граничит с воздухом, между хрусталиком и сетчаткой находится стекловидное тело. Оптические постоянные глаза для разных лиц колеблются в широких пределах поэтому были установлены средние значения для все; постоянных глаза. Глаз с указанными постоянными называется схематическим.
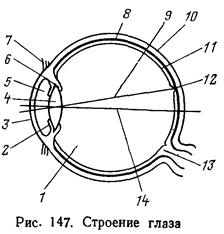
Глаз человека представляет собой своеобразный оптический прибор (рис. 147). Передняя, несколько выпуклая, часть оболочки глаза прозрачна и называется роговицей. в остальной части
глаз покрыт непрозрачной белковой оболочкой — склерой 10. Наружный покров роговицы переходит в конъюнктиву 7, прикрепленную к векам. За роговицей располагается передняя камера 5, наполненная прозрачной жидкостью, так называемой водянистой влагой. Заднюю стенку камеры образует р а- дужная оболочка 2 с отверстием посредине — зрачком. Диаметр зрачка меняется от.2 до 8 мм в зависимости от величины светового потока, поступающего в глаз.
За зрачком располагается хрусталик 4, который отделяет переднюю камеру 5 от задней камеры /. Хрусталик представляет собой двояковыпуклую эластичную линзу, на которую действуют кольцевая мышца 6, при этом изменяются кривизны поверхностей хрусталика, что позволяет фокусировать изображение предметов.
26. Закон обратимости световых лучей:
Пусть на какую-либо идеальную оптическую систему падает луч А и выходит из нее соответствующий ему луч В. Если пустить новый падающий луч навстречу В, получим новый выходящий из системы луч, идущий навстречу А.
Закон прямолинейности распространения света:
В однородной среде свет распространяется прямолинейно.
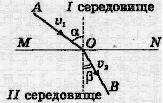
1. Луч падающий, перпендикуляр к границе двух сред в точке падения и луч отраженный лежат в одной плоскости. То, что две из перечисленных прямых лежат в одной плоскости, — не закон, так как любые две пересекающиеся прямые удовлетворяют этому геометрическому положению. Физическим содержанием закона является нахождение третьей прямой и той же плоскости. Следовательно, углы падения и отражения лежат в плоскости падения.
2. Угол падения равен углу отражения (изменяя произвольно угол падения, получаем такое же изменение угла отражения):
Луч падающий, перпендикуляр к границе двух сред в точке падения и преломленный луч лежат в одной плоскости (аналогично первому закону отражения, смысл этого закона в том, что третья из перечисленных прямых попала в плоскость, положение которой определяют первые две. Это плоскость падения).
Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данной пары сред (то есть не изменяется при произвольном изменении угла падения и соответственном изменении угла преломления). Эта постоянная называется показателем преломления (n21) второй среды относительно первой:
27. Методика решения задач с применением законов отражения и преломления света (на конкретных примерах).
Основная идея предлагаемой методики заключается вразделении решения на три этапа: физический, математическийи физико-математический. Физический этап– краткfz записm исходных данных и перевод физических величин в одну систему единиц (в нашем случае предпочтение отдаетсямеждународной системе, то есть СИ). Во втором разделе этого этапа необходимо сделать детальный эскиз (чертеж) с нанесением на нем всех исходных данных и сохранением уже принятых вусловии задачи обозначений. В третьем разделе физического этапа решения задачи необходимо проделать детальный предварительный анализусловия задачи, обозначив фундаментальные законы,теоретические предпосылки, другие, пусть даже малозначительные, закономерности и принципы, на которых базируется решение данной задачи. Сначала необходимо определить принадлежность задачи к тому или иному разделу физики, затем – фундаментальные законы, как правило,связанные с именем того или иного ученого, далее – конкретные правила либо принципы, с помощью которых удастся разрешить те или иные вопросы для вычисления искомой физическойвеличины. Таким образом, в этом разделе должен быть намечен конкретный алгоритм описания условий задачи на языке математических формул.В четвертом разделе физического этапа необходимо описать все явные и неявные данные, фигурирующие в задаче, на математическом языке, то есть в виде формул, и получить, в конечном счете, замкнутую систему математических уравнений. Желательно сопроводить краткими, но исчерпывающими пояснениями каждое уравнение будущей
системы. В полученной системе могут присутствовать подсистемы уравнений, и это даже облегчает дальнейшее решение задачи. Главное заключается втом, чтобы количество уравнений системы строго соответствовало количеству неизвестных переменных. Если такую систему удается получить, то первый этап решения задачи
– физический– считается завершенным. Математический этапсостоит из одного, но очень емкого раздела. Начинается он с анализа системы уравнений,поиска кратчайшего пути одновременного уменьшения количества уравнений и неизвестных. Здесь очень важна культура решения систем уравнений, которая должна взращиваться смладших классов общеобразовательной школы на уроках математики. Все вычисления производятся вобщем виде, следовательно, данный этап совершенно независимот физического этапа решения задачи и тем более – физико-математического. Завершается математический этап получением искомой величины в буквенных обозначениях величин, заданныхв условии задачи, включая различные константы. Таким способом получают аналитическое решениезадачи.На математическом этапе не завершается решение задачи.После получения формулы для расчета искомой величины необходимо перейти к физико-математическому этапурешения задачи. На этом этапе осуществляется проверка правильност иконечного результата. В первом разделе этого этапа проверяютразмерность (единицу измерения) искомой величины. Во втором разделе этого этапа проверяют разумность результата. При этом необходимо произвести анализ решениязадачи, то есть применить полученную формулу в различныхчастных случаях. Для этого требуется отдельные величины,входящие в конечную формулу, устремить либо к нулю, либо к бесконечности, а, может быть, к π/2 и т.п. Анализ решения должен продемонстрировать полную пригодность конечного результатадля частных случаев. Очень часто анализ решения помогает не только проверить правильность полученного результата, но и осознать (прочувствовать) фундаментальность физических законов, быстро запомнить многие формулы, а иногда даже предвосхитить решение будущих задач. Завершается решение задачи третьим разделом физико-математического этапа, в котором проверяется разумность числового значенияполученной величины. С этой целью в конечную формулу вместо буквенных символов величин необходимо подставить их числовые значения, выраженные, как было уже отмечено, в одной системе единиц. Полученное в этом разделе число вместе с ранее определенной единицей измерения составляют искомую физическую величину,которую следует сравнить с аналогичными величинами, взятыми
из справочника, например. Акцентирование внимания на реальных числовых значениях величин очень полезно для развития физического кругозора и быстрого приобщения к
многогранному миру физики. Подавляющее большинство физических задач имеют в условиях задачи реальные числовые значения физических величин. Первый закон преломления звучит так: отношение синуса угла падения к синусу угла преломления является постоянной величиной для данных двух сред:
Второй закон преломления света очень напоминает второй закон отражения света:
падающий луч, луч преломленный и перпендикуляр, проведенный в точку падения луча, лежит в одной плоскости.
Для характеристики линз используют величину, которая называется оптической силой.
Обозначают оптическую силу буквой D. За единицу оптической силы взята диоптрия (дптр).
Оптическую силу собирающих линз считают положительной, а рассеивающих линз – отрицательной
Формула тонкой линзы связывает между; собой три величины: расстояние от предмета до линзы d, расстояние от линзы до изображения f и фокус ное расстояние линзы F:
В формуле тонкой линзы фокусное расстояние ОF обозначается буквой F. Если линза собирающая, то > 0, если линза рассеивающая, то перед ставится знак «минус». Если изображение действительное, то > 0; если изображение воображаемое, то перед ставиться знак «минус». Все величины в формулу линзы подставляются в метрах.
Основная идея предлагаемой методики заключается в разделении решения на три этапа: физический, математический и физико-математический. Физический этап – краткfz записm исходных данных и перевод физических величин в одну систему единиц (в нашем случае предпочтение отдается международной системе, то есть СИ). Во втором разделе этого этапа необходимо сделать детальный эскиз (чертеж) с нанесением на нем всех исходных данных и сохранением уже принятых в условии задачи обозначений. В третьем разделе физического этапа решения задачи необходимо проделать детальный предварительный анализ условия задачи, обозначив фундаментальные законы, теоретические предпосылки, другие, пусть даже малозначительные, закономерности и принципы, на которых базируется решение данной задачи. Сначала необходимо определить принадлежность задачи к тому или иному разделу физики, затем – фундаментальные законы, как правило, связанные с именем того или иного ученого, далее – конкретные правила либо принципы, с помощью которых удастся разрешить те или иные вопросы для вычисления искомой физической величины. Таким образом, в этом разделе должен быть намечен конкретный алгоритм описания условий задачи на языке математических формул.В четвертом разделе физического этапа необходимо описать все явные и неявные данные, фигурирующие в задаче, на математическом языке, то есть в виде формул, и получить, в конечном счете, замкнутую систему математических уравнений. Желательно сопроводить краткими, но исчерпывающими пояснениями каждое уравнение будущей системы. В полученной системе могут присутствовать подсистемы уравнений, и это даже облегчает дальнейшее решение задачи. Главное заключается в том, чтобы количество уравнений системы строго соответствовало количеству неизвестных переменных. Если такую систему удается получить, то первый этап решения задачи – физический – считается завершенным. Математический этап состоит из одного, но очень емкого раздела. Начинается он с анализа системы уравнений, поиска кратчайшего пути одновременного уменьшения количества уравнений и неизвестных. Здесь очень важна культура решения систем уравнений, которая должна взращиваться с младших классов общеобразовательной школы на уроках математики. Все вычисления производятся в общем виде, следовательно, данный этап совершенно независим от физического этапа решения задачи и тем более – физико-математического. Завершается математический этап получением искомой величины в буквенных обозначениях величин, заданныв условии задачи, включая различные константы. Таким способо получают аналитическое решение задачи. На математическом этапе не завершается решение задачи. После получения формулы для расчета искомой величины необходимо перейти к физико-математическому этапу решения задачи. На этом этапе осуществляется проверка правильности конечного результата. В первом разделе этого этапа проверяют размерность (единицу измерения) искомой величины. Во втором разделе этого этапа проверяют разумность результата. При этом необходимо произвести анализ решения задачи, то есть применить полученную формулу в различных частных случаях. Для этого требуется отдельные величины, входящие в конечную формулу, устремить либо к нулю, либо к бесконечности, а, может быть, к π/2 и т.п. Анализ решения должен продемонстрировать полную пригодность конечного результата для частных случаев. Очень часто анализ решения помогает не только проверить правильность полученного результата, но и осознать (прочувствовать) фундаментальность физических законов, быстро запомнить многие формулы, а иногда даже предвосхитить решение будущих задач. Завершается решение задачи третьим разделом физико- математического этапа, в котором проверяется разумность числового значения полученной величины. С этой целью в конечную формулу вместо буквенных символов величин необходимо подставить их числовые значения, выраженные, как было уже отмечено, в одной системе единиц. Полученное в этом разделе число вместе с ранее определенной единицей измерения составляют искомую физическую величину, которую следует сравнить с аналогичными величинами, взятыми из справочника, например. Акцентирование внимания на реальных числовых значениях величин очень полезно для развития физического кругозора и быстрого приобщения к многогранному миру физики. Подавляющее большинство физических задач имеют в условиях задачи реальные числовые значения физических величин.
Предмет расположен на расстоянии 40 см от линзы, имеющей оптическую силу 5 дптр. Вторая линза с оптической силой 6 дптр расположена на расстоянии 60 см от первой линзы. Определите, где находится изображение и каково поперечное увеличение, даваемое оптической системой.
Ответ: Увеличение системы равно 5, так как первая линза не дает увеличения.