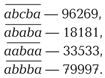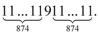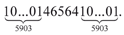Что такое палиндром в математике

Палиндромы и «перевёртыши» среди простых чисел

Числовой палиндром — это натуральное число, которое читается слева направо и справа налево одинаково. Иначе говоря, отличается симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным. Палиндромы встречаются в некоторых множествах чисел, удостоенных собственных названий: среди чисел Фибоначчи — 8, 55 (6-й и 10-й члены одноимённой последовательности); фигурных чисел — 676, 1001 (квадратное и пятиугольное соответственно); чисел Смита — 45454, 983389. Указанным свойством обладает также всякий репдиджит, например 2222222 и, в частности, репьюнит*.

Палиндром можно получить как результат операций над другими числами. Так, в книге «Есть идея!» известного популяризатора науки Мартина Гарднера в связи с этой задачей упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с обращённым числом, то есть записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не образуется палиндром. Иногда достаточно сделать всего один шаг (например, 312 + 213 = 525), но, как правило, требуется не менее двух. Скажем, число 96 порождает палиндром 4884 только на четвёртом шаге. В самом деле:

А суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.

Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:

До сих пор мы рассматривали в основном составные числа. Теперь обратимся к числам простым. В их бесконечном множестве имеются немало любопытных экземпляров и даже целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходятся на первую тысячу, из них четыре числа однозначные — 2, 3, 5, 7 и всего одно двузначное — 11. С такими числами связано немало интересных фактов и красивых закономерностей.

Во-первых, существует единственный простой палиндром с чётным числом цифр — 11. Другими словами, произвольный палиндром с чётным числом цифр, бóльшим двух, число составное, что нетрудно доказать на основе признака делимости на 11.

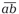
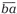
Во-вторых, первой и последней цифрами любого простого палиндрома могут быть только 1, 3, 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Любопытно, что все простые двузначные числа, записанные с помощью перечисленных цифр (за исключением 19), можно разбить на пары чисел-«перевёртышей» (взаимно обращённых чисел) вида и , где цифры a и b различны. Каждая из них, независимо от того, какое число стоит на первом месте, читается одинаково слева направо и справа налево:

Заглянув в таблицу простых чисел, мы обнаружим аналогичные пары, в записи которых присутствуют и другие цифры, в частности, среди трёхзначных чисел подобных пар наберётся четырнадцать.

Кроме того, среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1:

Аналогичная картина наблюдается и у бо`льших простых чисел, например:

Простые числа-палиндромы могут «задаваться» разными симметричными формулами, которые отражают особенности их записи. Это хорошо видно на примере пятизначных чисел:

Кстати, простые многозначные числа вида 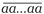встречаются, очевидно, только среди репьюнитов. Таких чисел известно пять. Примечательно, что у каждого из них количество цифр выражается простым числом: 2, 19, 23, 317, 1031. А вот среди простых чисел, у которых все цифры, кроме центральной, единицы, был обнаружен палиндром весьма внушительной длины — в нём 1749 цифр:

Вообще среди простых чисел-палиндромов встречаются удивительные экземпляры. Вот лишь один пример — числовой гигант

А интересен он тем, что содержит 11 811 цифр, которые можно разбить на три палидромические группы, причём в каждой группе количество цифр выражается простым числом (5903 или 5).

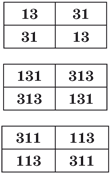
Любопытные палиндромические закономерности просматриваются и в группах простых чисел, в записи которых присутствуют определённые цифры. Скажем, только цифры 1 и 3, причём в каждом числе. Так, двузначные простые числа составляют упорядоченные пары 13 — 31 и 31 — 13, из шести трёхзначных простые сразу пять чисел, среди которых есть два палиндрома: 131 и 313, а ещё два числа образуют пары «перевёртышей» 311 — 113 и 113 — 311. Во всех этих случаях составленные пары наглядно представляются в виде числовых квадратов (рис. 1).

Своими свойствами они напоминают магический и латинский квадраты. Например, у среднего квадрата сумма чисел, стоящих в каждой строке и в каждом столбце, равна 444, на диагоналях — 262 и 626. Сложив числа из всех клеток, получим 888. И что характерно, каждая сумма — палиндром. Даже просто выписывая без пробела несколько чисел из одной таблицы, получим новые палиндромы: 3113, 131313131 и т. д. Какое наибольшее число можно составить таким способом? Будет ли оно палиндромом?

Если в каждую из пар 311 — 113 и 113 — 311 добавить 131 или 313, образуются четыре палиндромические тройки. Запишем одну из них в столбик:

Как видим, и сами числа, и нужная их комбинация дают о себе знать при прочтении в разных направлениях. Кроме того, расположение цифр симметрично, а их сумма в каждой строке, каждом столбце и на одной из диагоналей выражается простым числом − 5.

Надо сказать, рассмотренные числа интересны и сами по себе. Например, палиндром 131 — простое циклическое число: при любых последовательных перестановках первой цифры на последнее место он порождает простые числа 311 и 113. Можете ли вы указать другие простые палиндромы, обладающие таким же свойством?

А вот пары чисел-«перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:

(1 + 1 + 3) 2 = 1 + 2 + 7 + 6 + 9.

Добавим, что среди натуральных чисел имеются и другие пары «перевёртышей» с подобным свойством: 103 — 301, 1102 — 2011, 11113 — 31111 и др. Чем объясняется подмеченная закономерность? Чтобы ответить на этот вопрос, нужно понять, что особенного в записи указанных чисел, какие цифры и в каком количестве могут в ней присутствовать.

Из простых чисел-палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.

Вот, например, красивая комбинация из простых палиндромов, записанных с помощью 1 и 3 (кроме первого, рис. 2). Особенность этого числового треугольника в том, что один и тот же фрагмент повторяется трижды, не нарушая симметрию рисунка.

Легко видеть, что общее количество строк и столбцов — число простое (17). К тому же простые числа и суммы цифр: выделенных красным фрагментов (17); каждой строки, за исключением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и девятого столбцов (7, 11) и «лесенки» из единиц, образующей боковые стороны треугольника (11). Наконец, если двигаться параллельно указанным «сторонам» и складывать по отдельности цифры третьего и пятого рядов (рис. 3), получим ещё два простых числа (17, 5).

Продолжая построение, можно сконструировать на основе данного треугольника более сложные фигуры. Так, ещё один треугольник с аналогичными свойствами нетрудно получить, двигаясь с конца, то есть начать с последнего числа, вычёркивая на каждом шаге две одинаковые симметрично расположенные цифры и переставляя или заменяя другие — 3 на 1 и наоборот. При этом сами цифры следует выбирать с таким расчётом, чтобы образующееся в итоге число оказалось простым. Объединив обе фигуры, получим ромб с характерным узором из цифр, скрывающим в себе немало простых чисел (рис. 4). В частности, сумма выделенных красным цветом цифр равна 37.

Другой пример — треугольник, полученный из исходного после добавления к нему шести простых палиндромов (рис. 5). Фигура сразу привлекает внимание своим изящным обрамлением из единиц. Её окаймляют два простых репьюнита одинаковой длины: 23 единицы составляют «основание» и ещё столько же — «боковые стороны» треугольника.

Ещё несколько фигур

Можно составить также многоугольные фигуры из чисел, обладающие определёнными свойствами. Пусть требуется построить фигуру из простых палиндромов, записанных с помощью 1 и 3, у каждого из которых крайние цифры — единицы, а сумма всех цифр и общее количество единиц в строке — простые числа (исключение — однозначный палиндром). Кроме того, простым числом должно выражаться общее количество строк, а также цифр 1 либо 3, встречающихся в записи.

На рис. 6 приведено одно из решений задачи — «домик», сконструированный из 11 различных палиндромов.

Конечно, не обязательно ограничиваться двумя цифрами и требовать наличия в записи каждого используемого числа всех указанных цифр. Скорее, наоборот: ведь именно их необычные сочетания придают своеобразие узору фигуры. В подтверждение этому приведём несколько примеров красивых палиндромических зависимостей (рис. 7−9).

Теперь, вооружившись таблицей простых чисел, вы и сами сконструируете фигуры вроде предложенных нами.

А напоследок ещё одна диковинка — треугольник, буквально пронизанный вдоль и поперёк палиндромами (рис. 10). В нём 11 строк из простых чисел, а столбцы образованы репдиджитами. И главное: ограничивающий фигуру с боков палиндром 193111111323111111391 — число простое!

Комментарии к статье

*Число Смита — составное число, сумма цифр которого равна сумме цифр его простых делителей.

Репдиджит — натуральное число, в записи которого все цифры одинаковые.

Репьюнит — натуральное число, записанное с помощью одних только единиц.

Источник

Исследовательская работа ученицы 10 класса Калошиной Юлии на тему :»Палиндромы в математике»

Название работы: Палиндромы в математике

Автор работы: Калошина Юлия Сергеевна

Место выполнения работы: РК, Яшалтинский р-н, с. Яшалта,

МБОУ «Яшалтинская СОШ имени В. А. Панченко»

Глава 1. Понятие палиндрома в математике _______________________ 5

Глава 2. Формулы палиндромы ________________________________ 11

Глава 3. Именные палиндромы _________________________________ 13

Глава 4. Числовой конструктор _________________________________ 14

Глава 5. Палиндромы в других науках ____________________________ 15

Глава 6. Решение олимпиадных задач и задач ЕГЭ____________ ____ 17

Заключение __________________________________________________ 25

Список литературы ____________________________________________ 26

Обоснование выбора темы: Математика – один из моих любимых предметов, решение различных математических задач привлекало меня, начиная с начальных классов. Именно на уроках математики, при выполнении задач из сборника для подготовки к ЕГЭ, я встретила слово «палиндром». Мне стало интересно, что же это такое? Оказалось, это слово используется в разных науках и имеет множество значений. Я обратила внимание на то, что палиндромы есть как в русском языке, так и в математике. Удивилась: такие разные предметы, а слово одно используют. Но слово-то одно, а вот значения у него разные. Для начала нужно было узнать происхождение слова. Вот что я нашла в толковом словаре:

— Палиндром (греч. «бегущий обратно»), перевертень, «рачья песня» — последовательность звуков или букв, которые и в прямом, и в обратном порядке читаются одинаково: «оно», «я иду, судия». Палиндромом также называется и стих, который при прочтении слева направо или справа налево, дает те же слова. Другое, более точное и распространённое название таких фраз — зеркальные анаграммы. В математике и прочих науках встречаются числа, формулы — палиндромы.

Цели и задачи исследования:

1. Изучить литературу по теме исследования, анализ полученной информации;

2. Изучить свойства чисел- палиндромов;

3. Изучить формулы получения палиндромов при выполнении арифметических операций;

4. Рассмотреть палиндромы в других науках.

5. Создать сборник для подготовки к математическим олимпиадам и ЕГЭ.

Новизна исследования: написание программы на языке программирования Pascal для решения некоторых олимпиадных задач по теме «Палиндромы».

Практическая значимость : созданный мной сборник может использоваться учителями и учениками при подготовке к ЕГЭ; также окажется как нельзя, кстати, при решении задач выходящих за рамки школьной программы, олимпиадных заданий. А работа в целом будет способствовать повышению интереса к изучению математики у учеников и родителей.

Методы исследования: анкетирование; анализ литературы; синтез; сравнение; аналогия.

Гипотеза: После проведения опроса среди одноклассников, я задумалась об актуальности этой темы, ведь задачи по теме «Палиндромы», которых много в ЕГЭ и на олимпиадах, предполагают наличие определенных знаний у учеников; поэтому мне бы хотелось самой узнать как можно больше по этой теме и поделиться этими с другими. Я уверена, что если школьникам изучающим математику углубленно интересен и доступен материал по теме «Палиндромы», то и для нас это должно быть точно так же. Я предполагаю, что элементы высшей математики могут быть доступны и интересны ученикам средней школы. А также, исследуя множество натуральных чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.

Объект исследования : множество натуральных чисел

Предмет исследования: числа-палиндромы

Глава 1. Понятие палиндрома в математике

В математике существуют такие числа, которые образуют интересную подгруппу натуральных чисел. Их называют палиндромами. Они обладают необычной историей и имеют свои особенности, интересные свойства.

Говоря о том, что такое палиндром, следует сказать, что известны «перевертыши» с самой глубокой древности. Зачастую им придавался магический сакральный смысл. Появились палиндромы, примеры которых можно встретить в самых разных языках, предположительно в средние века. Древнейший известный палиндром — фраза на латыни, датирующаяся 4 веком н. э.: «SatorArepotenetoperarotas», переводящаяся как «Сеятель Арепо с трудом держит колёса». Фраза обычно записывается в квадрате 5×5, где обнаруживается ещё одно свойство симметрии — её можно читать как по горизонтали, так и по вертикали.

Числовые палиндромы – это натуральные числа, которые одинаково читаются справа налево и слева направо. Математики связывают с ними множество любопытных фактов и закономерностей: так, палиндромы делятся на пары и семейства, образуют числовые квадраты и целые симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.

В математике палиндромом называется строка a1a2…an, для которой выполняются равенства a1=an, a2=an-1, …, a[n-2]=an+1-[n-2], где a1, a2, …, an — некоторые символы. В частности, палиндромами являются все строки из одного символа, а также пустая строка (строка из 0 символов). При этом не обязательно, чтобы строка была осмысленным словом или выражением. С другой стороны, расстановка пробелов в математическом палиндроме тоже должна быть симметричной. Также палиндромам в математике посвящены некоторые теоремы. Вот одна из них:

Теорема : Самой длинной палиндромной подстрокой строки s1s2…sn является самая длинная общая подстрока строк s1s2…sn и sn…s2s1. Если таких общих подстрок несколько, то все они являются палиндромами. (Подстрокой строки S называется строка, полученная из S вычёркиванием некоторых символов без перестановки оставшихся.)

Например, палиндромом является квадрат числа состоящего из единиц 1^2=1 11^2=121 111^2=12321 1111^2=1234321 11111^2=123454321 1*n+1=палиндром

Назовем исходное число и число с переставленными в обратном порядке цифрами взаимно обратными. Выяснено, что сложение некоторых взаимно обратных чисел приводит к образованию числа-палиндрома. Но для многих взаимно обратных чисел такое число палиндром при сложении не образуется. А что будет, если в этом случае сложить результат сложения с его взаимно обратным числом?

Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:

Обратимся к числам простым. В их бесконечном множестве имеются целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходится на первую тысячу, из них четыре числа однозначные – 2; 3; 5; 7 и всего одно двузначное – 11.

С такими числами связано немало интересных закономерностей:

Существует единственный простой палиндром с чётным числом цифр – 11.

1.Первой и последней цифрами любого простого палиндрома могут быть только 1; 3; 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Все простые двузначные числа, записанные с помощью перечисленных цифр (кроме 19), можно разбить на пары.

Например: 13 и 31; 17 и 71; 37 и 73; 79 и 97.

2. Среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1.

Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929.

Аналогичная картина наблюдается у больших простых чисел.

Например: 94849 и 94949; 1177711 и 1178711.

3. Все однозначные числа являются палиндромами.

4. 26 – наименьшее число, не являющееся палиндромом, квадрат которого палиндром. Например: 26² = 676

Вообще среди простых чисел-палиндромов встречаются удивительные экземпляры. Вот лишь один пример — числовой гигант

5903 раза 5903 раза

А интересен он тем, что содержит 11 811 цифр, которые можно разбить на три палидромические группы, причём в каждой группе количество цифр выражается простым числом (5903 или 5).

Любопытные палиндромические закономерности просматриваются и в группах простых чисел, в записи которых присутствуют определённые цифры. Скажем, только цифры 1 и 3, причём в каждом числе. Так, двузначные простые числа составляют упорядоченные пары 13 — 31 и 31 — 13, из шести трёхзначных простые сразу пять чисел, среди которых есть два палиндрома: 131 и 313, а ещё два числа образуют пары «перевёртышей» 311 — 113 и 113 — 311. Во всех этих случаях составленные пары наглядно представляются в виде числовых квадратов (рис. 1).

Своими свойствами они напоминают магический и латинский квадраты. Например, у среднего квадрата сумма чисел, стоящих в каждой строке и в каждом столбце, равна 444, на диагоналях — 262 и 626. Сложив числа из всех клеток, получим 888. И что характерно, каждая сумма — палиндром. Даже просто выписывая без пробела несколько чисел из одной таблицы, получим новые палиндромы: 3113, 131313131 и т. д. Если в каждую из пар 311 — 113 и 113 — 311 добавить 131 или 313, образуются четыре палиндромические тройки. Запишем одну из них в столбик:

Как видим, и сами числа, и нужная их комбинация дают о себе знать при прочтении в разных направлениях. Кроме того, расположение цифр симметрично, а их сумма в каждой строке, каждом столбце и на одной из диагоналей выражается простым числом − 5.

Надо сказать, рассмотренные числа интересны и сами по себе. Например, палиндром 131 — простое циклическое число: при любых последовательных перестановках первой цифры на последнее место он порождает простые числа 311 и 113. Можете ли вы указать другие простые палиндромы, обладающие таким же свойством?

А вот пары чисел-«перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:

(1 + 1 + 3) 2 = 1 + 2 + 7 + 6 + 9. Добавим, что среди натуральных чисел имеются и другие пары «перевёртышей» с подобным свойством: 103 — 301, 1102 — 2011, 11113 — 31111 и др.

Глава 2.Формулы – палиндромы.

Под формулами – палиндромами, понимают, выражение (состоящее из суммы или разности чисел), результат которого не меняется в результате прочтения выражения справа налево.

Если сложить числа – палиндромы, то сумма не меняется.

В общем виде это можно записать так:

(100х + 10х+ x ) + (100у + 10 y + у) = (100у + 10 y + у) + (100х + 10 x + х)

100х + 10х+ x + 100у + 10у + y = 100у + 10у + y + 100 x +10х + х

111х + 111у = 111у + 111х

От перестановки слагаемых сумма не изменяется (переместительное свойство сложения).

Задача 1. Найти все пары таких двузначных чисел, чтобы результат их сложения не менялся в результате прочтения суммы справа налево, то есть

Например, 42 + 35 = 53 + 24.

Любое двузначное число можно представить в виде суммы разрядных слагаемых:

Примеры: 41-32 = 23-14, 62-17 = 71-26

Примеры: 39*31=13*93, 42*12=21*24

х1у1/х2у2 =у2х2/у1х1, тогда имеем

х1*у2=х2*у1, т.е.произведение первой цифры первого числа на вторую цифру второго числа равно произведению двух других их цифр.

Глава 3. Именные палиндромы.

Палиндромы встречаются в некоторых множествах чисел, удостоенных собственных названий: число Фибоначчи, число Смита, Репдиджит, Репьюнит.

Числами Фибоначчи называют элементы числовой последовательности. В ней каждое следующее число в ряду получается суммированием двух предыдущих чисел.

Число Смита — составное число, сумма цифр которого равна сумме цифр его простых делителей.

Репдиджит — натуральное число, в записи которого все цифры одинаковые.

Например, 4444, 5555555 и т.д.

Треугольником Паскаля называется бесконечная треугольная таблица, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строк

Например, числа (121,15101051 и т.д.)

Глава 4. Числовой конструктор.

Из простых чисел-палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.

Вот, например, красивая комбинация из простых палиндромов, записанных с помощью 1 и 3 (кроме первого, рис. 2). Особенность этого числового треугольника в том, что один и тот же фрагмент повторяется трижды, не нарушая симметрию рисунка.

Рис. 2

Легко видеть, что общее количество строк и столбцов — число простое (17). К тому же простые числа и суммы цифр: выделенных красным фрагментов (17); каждой строки, за исключением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и девятого столбцов (7, 11) и «лесенки» из единиц, образующей боковые стороны треугольника (11). Наконец, если двигаться параллельно указанным «сторонам» и складывать по отдельности цифры третьего и пятого рядов (рис. 3), получим ещё два простых числа (17, 5).

рис.3

Глава 5. Палиндромы в других науках.

Рассмотрим палиндромы в других науках:

1. В изобразительном искусстве:

Палиндромы в биологическом смысле обладают способностью обеспечивать увеличение объема информации без повышения количества нуклеотидов. Особое значение «симметричные формы» имеют при образовании некоторых видов нуклеиновых кислот – транспортных РНК.

— Лилипут сома на мосту пилил.

— Нажал кабан на баклажан.

На это дама скромно может ответить «перевертышем»: «Eve» (Ева).

Бывают симметричными не только предложения или наборы букв:

Race fast, safe car (Гони быстро, безопасная машина)

Never odd or even (Никогда нечётные или чётные)

Палиндромные музыкальные произведения играются «как обычно», в соответствии с правилами. После завершения пьесы ноты переворачиваются. Затем произведение играют снова, но мелодия при этом не будет меняться. Итераций может присутствовать сколько угодно, неизвестно при этом, что является низом, а что – верхом. Данные музыкальные произведения можно сыграть вдвоем, при этом читая ноты с обеих сторон одновременно. В качестве примеров таких палиндромических произведений можно привести «Путь мира», написанный Мошелесом, и «Застольную мелодию для двоих», сочиненную Моцартом.

Глава 6. Решение олимпиадных задач и задач ЕГЭ.

А) Приведите пример числа – палиндрома, которое делится на 55. Б) Сколько существует пятизначных чисел – палиндромов, делящихся на 55? в) Найдите 13-е по величине число – палиндром, которое делится на 55.

Б)Теперь займемся пятизначными числами. Ищем число вида 5хух5, которое делится на 55. Попробуем воспользоваться признаками делимости. Число 55=5*11. Поэтому искомые числа должны делиться на 11. «Число делится на11, если сумма цифр, стоящих на нечетных местах равняется сумме цифр, стоящих на четных местах или отличается от нее на11».

Имеем: 5+у+5=х+х или 5+у+5=х+х+11. Получим:

10+у=2х – решением этого уравнения являются пары чисел: (5;0), (6, 2), (7, 4), (8, 6), (9, 8).

10+у=2х+11 – решением этого уравнения являются пары чисел (0,1), (1,3), (2,5), (3,7), (4,9).

Получим 10 чисел – палиндромов:

Таким образом, среди пятизначных чисел ровно 10 палиндромов.

В)назовите 13 –е по счету число-палиндром, которое делится на 55.

Если ряд палиндромов начать с числа 55, то тринадцатым будет 51315.

55, 5005, 5115,5225,5335,5445,5555,5665,5775,5885,5995. 50105. 51315, 52525,53735,54945,55055,56265,57475,58685,59895

а) Приведите пример числа-палиндрома, который делится на 15. б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15? в) Найдите 37-е по величине число-палиндром, которое делится на 15.

1)При Z =0 получается 5 y 0 y 5

2)При Z =1 получается 5+ y +1+ y +5=11+2 y

При y =1 51015 При y =2 52125

При y =454045 При y =5 55155

При y =7 57075 При y =858185

3) При Z =2 получается 12+2 y /3 4) При Z =3 получается 13+2 y /3

При y =0 50205 При y =1 51315

При y =353235 При y =4 54345

При y =656265 При y =7 57375

Таким образом, заметим повторение.

Для набора y =(1,4,7)= z =0,3,6,9 (12 чисел)

Для набора y =(2,5,8) )= z =1,4,7 (9 чисел)

Для набора y =(0,3,6,9)= z =2,5,8( 12 чисел)

В)Найдем 37-е по счету число палиндром

1)При двузначных нет палиндромов/15

2)Среди 3-значных 5 y 5 y =2,5,8 525,555,585

4)Среди 5-значных выписываем все числа

5)Упорядочиваем все числа и находим 37 –е число по счету

Ответы: а) 5115; б) 33; в) 59295

Решение : аналогично предыдущей задаче.

Ответ :а)585; б)11 ;в)56565

Задача 4. Автомобилист посмотрел на счетчик своего автомобиля и увидел симметричное число (палиндром) 15951 км (читается одинаково слева направо или наоборот). Он подумал, что, скорее всего, уже не скоро появится другое симметричное число. Однако уже через 2 часа он обнаружил новое симметричное число. С какой постоянной скоростью автомобилист проехал эти два часа?

Сколько существует 5-значных палиндромов, делящихся на 9.

Задача 6: . Представьте число 2015 в виде суммы двух палиндромов.

Решение: 2015=1551+464. Догадаться нетрудно. Самый большой трехзначный палиндром это 999. Но 999+999=1998

Если дату 10 февраля 2001 года записать в виде 10.02.2001, а затем убрать точки, то получится палиндром (т.е. число, читающееся слева направо и справа налево одинаково). Найдите ближайшую к 10.02.2001 дату, обладающую тем же свойством. Решение: Рассмотрим два случая:
1) требуемая дата еще не наступила,
2) требуемая дата уже прошла.
Итак, 1) в 2001 году других палиндромов быть не может, а в следующем (2002) году это должен быть 20 день второго месяца.

Ответ. 1) 20 февраля 2002 2) 29 ноября 1192 года.

а) двузначных ; б) трехзначных ; в) четырехзначных ; г) пятизначных

На 2 делится любое четное число. Поэтому,

Задача 9:

б) трехзначных ; в) четырехзначных ; г) пятизначных

Решение: На 3 число делится, если сумма его цифр делится на 3.

а) среди двухзначных таких чисел 3: 33, 66 и 99.

Источник