Что такое хроматическое число графа

Хроматическое число планарного графа

Содержание

Раскраска в 6 цветов [ править ]

Докажем по индукции.

Если граф содержит не более [math]6[/math] вершин, то очевидно, что [math] \chi (G) \leqslant 6.[/math]

Предположим, что для планарного графа с [math]N[/math] вершинами существует раскраска в [math]6[/math] цветов. Докажем то же для графа с [math] N+1 [/math] вершиной.

Вернём удалённую вершину и покрасим её в цвет, не встречающийся среди смежных ей вершин (ведь «занято» максимум [math]5[/math] цветов). Индукционный переход доказан.[math]\triangleleft[/math]

Раскраска в 5 цветов [ править ]

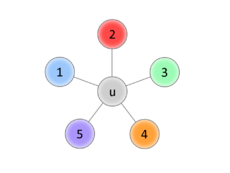
Обозначим за [math] u [/math] — возвращаемую вершину, [math] v^ <(k)>[/math] — вершину, покрашенную в [math] k [/math] цвет.

Иначе, уложим полученный после удаления [math] u [/math] граф на плоскость, вернём вершину [math] u [/math] (пока бесцветную) и пронумеруем цвета в порядке обхода смежных вершин по часовой стрелке.

Заметим, что не удаётся составить подобное доказательство для раскраски в четыре цвета, поскольку здесь наличие двух вершин одного цвета среди смежных [math] u [/math] не исключает того, что при их (смежных вершин) раскраске использовались все возможные цвета.

Раскраска в 4 цвета [ править ]

Теорема о четырёх красках была доказана в [math]1976[/math] году Кеннетом Аппелем и Вольфгангом Хакеном из Иллинойского университета. Это была первая крупная математическая теорема, доказанная с помощью компьютера. Первым шагом доказательства была демонстрация того, что существует определенный набор из [math]1936[/math] карт, ни одна из которых не может содержать карту меньшего размера, которая опровергала бы теорему. Аппель и Хакен использовали специальную компьютерную программу, чтобы доказать это свойство для каждой из [math]1936[/math] карт. Доказательство этого факта заняло сотни страниц. После этого Аппель и Хакен пришли к выводу, что не существует наименьшего контрпримера к теореме, потому что иначе он должен бы содержать, хотя не содержит, какую-нибудь из этих [math]1936[/math] карт. Это противоречие говорит о том, что вообще не существует контрпримера. Изначально доказательство не было принято всеми математиками, поскольку его невозможно было проверить вручную. В дальнейшем оно получило более широкое признание, хотя у некоторых долгое время оставались сомнения.

Чтобы развеять оставшиеся сомнения, в [math]1997[/math] году Робертсон, Сандерс, Сеймур и Томас опубликовали более простое доказательство, использующее аналогичные идеи, но по-прежнему проделанное с помощью компьютера. Кроме того, в [math]2005[/math] году доказательство было проделано Джорджсом Гонтиром с использованием специализированного программного обеспечения (Coq v7.3.1)

Эквивалентные формулировки [ править ]

В теории графов утверждение теоремы четырёх красок имеет следующие формулировки:

Ложное доказательство [ править ]

Карта(слева) окрашена пятью цветами, и нужно изменить как минимум [math]4[/math] из [math]10[/math] регионов, чтобы получить окраску в четыре цвета(справа)

Источник

Хроматическое число

Хроматическое число графа G — минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Обозначается χ(G).

Содержание

Определение

Хроматическое число графа — минимальное число , такое что множество вершин графа можно разбить на непересекающихся классов :

таких, что вершины в каждом классе независимы, то есть любое ребро графа не соединяет вершины одного и того же класса.

Связанные определения

Реберная раскраска

Хроматический класс графа G — минимальное число цветов, в которые можно раскрасить ребра графа G так, чтобы смежные ребра имели разные цвета. Обозначается χ'(G). Проблема реберной раскраски произвольного плоского кубического графа без мостов тремя цветами эквивалентна знаменитой Проблеме четырех красок. Реберная раскраска определяет 1-факторизацию графа.

Хроматический многочлен

Если рассмотреть количество различных раскрасок помеченного графа как функцию от доступного числа цветов t, то оказывается, что эта функция всегда будет полиномом от t. Этот факт был обнаружен Биркгофом и Льюисом [1] при попытке доказать гипотезу четырех красок.

Хроматические многочлены некоторых графов

Треугольник
Полный граф
Дерево с вершинами
Цикл
Граф Петерсена

Нахождение хроматического многочлена произвольного графа

Для графа-вершины хроматический многочлен равен

Хроматический многочлен графа равен произведению хроматических многочленов его компонент

Также существует рекуррентное соотношение

где и — смежные вершины, — граф, получающийся из графа путем удаления ребра а — граф, получающийся из графа путем стягивания ребра в точку.
Можно использовать эквивалентную формулу

где и — несмежные вершины, а — граф, получающийся из графа путем добавления ребра

Свойства хроматического многочлена

Для всех целых положительных

Хроматическое число — наименьшее целое положительное , для которого

0.» border=»0″ />

Обобщения

Значение для теории графов

Множество глубоких задач теории графов легко формулируются в терминах раскраски. Самая знаменитая из таких задач, проблема четырёх красок, в настоящее время решена, однако появляются новые, например, обобщение проблемы четырёх красок, гипотеза Хадвигера.

См. также

Примечания

Литература

Полезное

Смотреть что такое «Хроматическое число» в других словарях:

Хроматическое число — [chro­matic number] число, характеризующее количество несмежных вершин графа. Если пометить все вершины графа р цветами (отсюда и термин“хроматическое”) и при этом никакие две смежные вершины не будут окрашены одинаково, то такой граф называется… … Экономико-математический словарь

хроматическое число — Число, характеризующее количество несмежных вершин графа. Если пометить все вершины графа р цветами (отсюда и термин“хроматическое”) и при этом никакие две смежные вершины не будут окрашены одинаково, то такой граф называется хроматическим… … Справочник технического переводчика

Раскраска графа — 3 раскраска графа Петерсена Хроматическое число графа G минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Обозначается χ(G). Содержание 1 Определение … Википедия

Раскрашиваемый граф — 3 раскраска графа Петерсена Хроматическое число графа G минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Обозначается χ(G). Содержание 1 Определение … Википедия

Хроматический граф — 3 раскраска графа Петерсена Хроматическое число графа G минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Обозначается χ(G). Содержание 1 Определение … Википедия

Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия

Инвариант графа — в теории графов некоторое обычно числовое значение или упорядоченный набор значений (хэш функция), характеризующее структуру графа и не зависящее от способа обозначения вершин или графического изображения графа. Играет важную роль при… … Википедия

Нерешённые проблемы математики — Нерешённые проблемы (или Открытые проблемы) проблемы, которые рассматривались математиками, но до сих пор не решены. Часто принимают форму гипотез, которые предположительно верны, но нуждаются в доказательстве. В научном мире популярна практика… … Википедия

Открытые математические проблемы — Открытые (нерешённые) математические проблемы проблемы, которые рассматривались математиками, но до сих пор не решены. Часто имеют форму гипотез, которые предположительно верны, но нуждаются в доказательстве. В научном мире популярна… … Википедия

Источник

Хроматическое число плоскости не меньше 5

Задача о хроматическом числе плоскости формулируется следующим образом: в какое наименьшее число цветов можно раскрасить плоскость так, чтобы любые две точки на расстоянии 1 были покрашены в различные цвета?

Эту задачу сформулировали Хуго Хадвигер и Пал Эрдёш в сороковых годах XX века. Независимо от них примерно в то же самое время этой задачей занимались Эдуард Нелсон и Дж. Р. Исбелл. После работы Хадвигера 1961 года об открытых на тот момент проблемах, хроматическое число плоскости стало активно изучаться.

Сразу же было показано, что в 3 цвета плоскость требуемым образом раскрасить нельзя, однако 7 цветов достаточно. Действительно, легко выбрать на плоскости несколько точек так, что некоторые из них находятся на расстоянии ровно 1 (такая конструкция точек называется графом единичных расстояний), и затем перебором показать, что в 3 цвета эти точки раскрасить невозможно. Примеры таких графов — веретено Мозера и граф Голомба приведены на картинке ниже. Чтобы показать, что 7 цветов достаточно, замостим плоскость правильными шестиугольниками со стороной 0.4 и закрасим их по определённому паттерну, как на картинке ниже. Тогда, как несложно убедиться, концы любого отрезка длины 1 будут лежать в разных шестиугольниках различных цветов.

Однако, с тех пор никто не мог уточнить ни верхнюю, ни нижнюю границы. Задача получила название Проблема Нелсона — Эрдёша — Хадвигера. Прошло 60 лет, и вот, в апреле 2018 года математик-любитель Обри де Грей предъявил граф единичных расстояний, который нельзя покрасить в 4 цвета.

Геронтология и математика

Обри Дэвид Николас Джаспер ди Грей — британский геронтолог, исследует различные аспекты старения человека. Является разработчиком концепции SENS — «стратегии достижения пренебрежимого старения инженерными методами» (strategies for engineered negligible senescence). Председатель и директор по науке Фонда SENS, главный редактор академического журнала «Rejuvenation Research». Автор научно-популярной книги «Ending Aging», в которой в деталях рассматривается вопрос о полной победе над старением средствами медицины в течение ближайших нескольких десятилетий. (инфо из вики)

Как оказалось, этот почтенный бородатый дядька ещё и увлекается математикой в свободное время. 8 апреля 2018 года он выложил на arXiv статью, в которой описывает способ построения графа единичных расстояний, для покраски которого нужно как минимум 5 цветов.

Давайте разберёмся подробнее, что же это за граф такой.

Граф, который построил Джек

Всё начинается с простого графа H, состоящего из 7 вершин и 12 рёбер:

Давайте попробуем раскрасить его не более чем в 4 цвета всевозможными способами. Оказывается, различных способов это сделать (с точностью до поворотов, отражений и порядка цветов) всего 4:

Заметим, что в верхних двух вариантах у нас есть тройки одноцветных вершин, которые расположены в вершинах правильного треугольника, а в нижних двух — нет. Назовём раскраску графа H плохой, если там есть такая одноцветная тройка, иначе раскраска H — хорошая. Итого, у нас 2 плохие раскраски и 2 хорошие.

Хорошо, идём дальше. Рассмотрим граф J, склеенный из 13 графов H (найдите их все!):

Давайте попробуем покрасить граф J так, чтобы покраски всех входящих в него подграфов H были хорошие. Немного терпения, и мы получаем 6 различных вариантов (опять же с точностью до всяких эквивалентных преобразований, указанных выше; плюс цветов вершин, отмеченных чёрным):

Чёрные вершины могут быть покрашены несколькими способами, но их покраска нам не особо важна. Тем не менее, выкидывать их из графа J нежелательно — тогда появляются «лишние» варианты покраски. Которые, к тому же, портят все дальнейшие построения. Поэтому пусть чёрные вершины остаются.

Теперь давайте внимательно посмотрим на получившиеся варианты. А именно, на центральную вершину и на 6 вершин, удалённых от центральной на расстояние 2 (этаких граф H, увеличенный в два раза). Мы видим, что там всегда используется не более двух цветов. Более того, все варианты можно разбить на 3 случая:

Уже становится немного сложно, не правда ли?

Теперь давайте опять немного помедитируем на получившуюся конструкцию. А именно давайте поймём какие типы раскрасок у каждой копии графа J могли быть из тех трёх, что были перечислены выше. Типа a) раскраски там нет, так как какой бы тип ни был у второй копии, мы получим две вершины одного цвета на расстоянии 1. Типа b) там тоже нет: если у второй копии тоже тип b), то какие-то 2 вершины цвета центра «мешают» друг на другу; если у второй копии тип c), то хотя бы одна вершина на концах одноцветной диагонали будет соответствовать одной из четырёх вершин первой копии. Стало быть, у обеих копий графа J тип покраски c)! И такие покраски возможны, поскольку 4 вершины, которые покрашены в цвет, отличный от центрального, хотя и имеют один цвет, в каждой из копий этот цвет может быть разным.

Теперь, раз у двух копий графа J в графе K тип c), то пары противоположных вершин (из 6 нами рассматриваемых в каждой копии) имеют один и тот же цвет. Воспользуемся этим наблюдением и сделаем ещё один шаг. А именно, построим граф L из двух копий графа K:

Мы накладываем графы K друг на друга следующим образом: берём в каждом из них пару противоположных вершин и первые вершины в каждой паре совмещаем (на картинке выше это отмечено буквой A), а вторые размещаем на расстоянии ровно 1 (они отмечены буквами B и C). Этот приём называется оверетенением графа (от англ. spindling, где spindle — веретено). Например, веретено Мозера — это оверетенение графа-ромбика, составленного из двух треугольников. По наблюдению чуть выше, вершины A, B и C должны быть одного цвета, B и C на расстоянии 1, значит граф L покрасить нельзя.

Итак, что же, мы всё доказали? Да нет же, мы только доказали, что граф L нельзя покрасить в 4 цвета так, чтобы покраски всех копий графа H (а их уже насчитывается 52 штуки!) были хорошими. Значит, в любой покраске графа L покраска хотя бы одного графа H будет плохой!

Плохие покраски графа H

С этой частью, к сожалению, нельзя разобраться без помощи компьютера. Поэтому разберём кратко дальнейшую часть построений, за деталями можно обратиться к оригинальной статье, либо по ссылкам на Polymath чуть ниже. Картинки, взятые из оригинальной статьи, не очень высокого качества, но они позволяют примерно понять, что происходит.

Итак, сначала мы строим граф V на 31 вершину, который состоит из 5 графов H, которые совмещены центрами и повёрнуты на хитрые углы друг относительно друга:

Далее мы строим граф W следующим образом: делаем 31 копию графа V и помещаем центр каждой копии в каждую вершину ещё одного графа V (такая операция называется суммой Минковского двух графов единичных расстояний, т.е. мы делаем ), после чего удаляем все вершины, которые удалены от центра на расстояние больше . Итого теперь у нас есть граф W на 301 вершину:

Теперь берём граф H и заменяем каждую его вершину на копию графа W (т.е. делаем ). В итоге получаем граф M на 1345 вершин:

Полученный граф M в сущности является объединением большой кучи веретён Мозера в различных положениях. И, если мы покрасим в один цвет три вершины на попарном расстоянии изначального графа H, который мы распушивали до M, тем самым сделав покраску H плохой, то остальную часть графа M покрасить в 4 цвета не получится. Этот факт проверяется компьютерным перебором.

И, наконец, последний шаг: мы теперь берём вот эту жесть M на 1345 вершин и копируем поверх каждой из 52 копии графа H в графе L. В итоге получаем полную жесть на 20425 вершин, которая называется граф N. И этот граф нельзя покрасить в 4 цвета: при покраске каркаса L покраска хотя бы одного из подграфов H получится плохой, и для этого подграфа H соответствующую копию M докрасить до конца не получится.

Что и требовалось доказать.

Уменьшенный граф

Граф на 20425 вершин — довольно большой граф. Можно ли построить пример поменьше? Можно! Ещё в оригинальной статье де Грей различными отсечками уменьшил пример до 1581 вершины.

После публикации статьи, математическое сообщество организовало проект Polymath16 (как это было, например, с задачей про простые числа близнецы) для того, чтобы коллективными усилиями уменьшить граф, полученный де Греем, обобщить результат на большие размерности (для трехмерного пространства, четырехмерного, и так далее), а то и улучшить нижнюю границу хроматического числа для плоскости до 6.

Кстати, там же независимо проверили при помощи SAT-солверов, что пример де Грея на 1581 вершину действительно можно покрасить только в 5 цветов, а также то, что его граф является графом единичных расстояний. Так что сомнений в корректности полученного результата нет.

Граф де Грея потихоньку уменьшают. Например, граф L на 121 вершину и 52 копии графа H можно слегка уменьшить до графа L’ на 97 вершин и 40 копий графа H. Граф M с 1345 вершинами был уменьшен до графа M’ с всего 278 вершинами.

После замещения всех подграфов H на M’ а графе L’, результат можно улучшать и далее. На момент написания данной статьи наименьший найденный граф единичных расстояний, который нельзя покрасить в 4 цвета, имеет 610 вершин. Вот его картинка (кликабельно):

Работа продолжается. Может быть в скором времени удастся построить граф единичных расстояний, который нельзя покрасить в 5 цветов. А затем — в 6, и тогда задача о хроматическом числе плоскости будет решена полностью.

Источник

В поисках хроматического числа

Российский математик опроверг гипотезу Стефана Хидетниеми

Несколько дней назад сообщество математиков — специалистов в теории графов было взволновано сообщением о том, что выдвинутая Стефеном Хидетниеми (Stephen T. Hedetniemi) в 1966 году гипотеза оказалась неверной. Оказывается, хроматическое число тензорного произведения двух графов может быть меньше минимума хроматических чисел сомножителей, а не всегда равно этому минимуму, как когда-то предположил Хидетниеми. Как построить контрпример к этой гипотезе, придумал молодой московский математик Ярослав Шитов. Подробнее об этом по просьбе N + 1 рассказал математик Владимир Потапов.

Хроматическое число графов

Расскажем подробнее о том, что такое хроматическое число графа, тензорное произведение графов и почему более 50 лет эта гипотеза казалась верной большинству специалистов.

Начнем с того, что графом в математике называется набор точек (вершин графа), соединенных отрезками (ребрами графа). Раскраска вершин графа в разные цвета называется правильной, если вершины, соединенные ребром (смежные вершины), раскрашены в разные цвета.

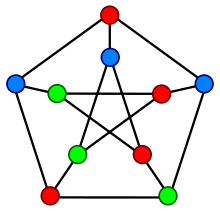
Хроматическим числом графа называется минимальное число цветов, которыми можно правильно раскрасить вершины графа. Нетрудно видеть, что изображенный выше граф Петерсена нельзя правильно раскрасить в два цвета, поскольку в нем есть циклы нечетной длины. Следовательно, его хроматическое число равно 3.

Задача нахождения хроматического числа графа стала популярной благодаря широко известному вопросу: «Можно ли вершины плоского (то есть размещенного на плоскости без пересечений ребер) графа правильно раскрасить в 4 цвета?»

Гипотеза «четырех красок», которая состоит в положительном ответе на этот вопрос, возникла еще в XIX веке и была доказана Кеннетом Аппелем и Вольфгангом Хакеном только в 1977 году. Причем в доказательстве авторам пришлось прибегнуть к компьютеру, чтобы правильно раскрасить сотни графов, раскраска которых уже не сводилась к раскраске более простых графов. Кстати, граф Петерсена плоским не является и может быть нарисован на плоскости только с пересечениями ребер.

Может показаться, что игры в раскрашивание графов не могут иметь никакого полезного применения. Даже практический вопрос: сколько необходимо цветов, чтобы любые соседние страны на карте были разного цвета? — из которого возникла гипотеза о «четырех красках», кажется скорее праздным, чем полезным. Однако по мере роста сложности инфраструктуры и оборудования оказалось, что имеется множество вполне серьезных задач, которые сводятся к нахождению хроматического числа графа.

Например, недалеко расположенные станции сотовой связи должны работать на разных радиочастотах, чтобы не мешать друг другу. Если станции связи считать вершинами графа и соединить ребрами те пары станций, которые могут мешать работе друг друга, то хроматическое число графа будет равно минимально необходимому набору различных радиочастот для безотказной работы сотовой связи.

Если же рассмотреть социальную сеть Facebook как граф с вершинами — пользователями, каждая из которых смежна с «друзьями», то становится ясно, что изучение различных характеристик графов важно для понимания закономерностей распространения информации (новостей, моды, инноваций) в современном мире.

Произведения графов

Прежде чем перейти к обсуждению гипотезы Хидетниеми, поговорим о понятии декартова произведения графов. Пусть имеются два графа G и H с множествами вершин 1…u_n> и 1…v_m> соответственно. Тогда их декартовым произведением называется граф, вершины которого являются всевозможными парами (u_i,v_k). Причем вершины (g,h) и (b,d) соединены ребром, только если g=b и вершина h смежна с вершиной d в графе H или, наоборот, h=d и вершина g смежна с вершиной b в графе G.

Декартово произведение графов

Легко понять, что хроматическое число декартова произведения графов не меньше, чем хроматическое число любого из сомножителей. Если мы зафиксируем любую вершину h графа H и рассмотрим в декартовом произведении вершины вида (u,h), а также ребра между ними, то получится такой же подграф, как граф G. Значит, для правильной раскраски этого подграфа нужно столько же цветов, сколько для правильной раскраски графа G, а для правильной раскраски всего декартова произведения цветов нужно точно не меньше. То же самое можно сказать и про граф H.

Более 50 лет назад математик Герт Сабидусси доказал, что хроматическое число декартова произведения графов равно максимуму хроматических чисел сомножителей.

Теперь перейдем к тензорному произведению графов, о котором говорится в гипотезе Хидетниеми. Тензорным произведением графов G и H называется граф с теми же вершинами, что и у декартова произведения графов G и H, которые, однако, по-другому соединены ребрами. А именно, вершины (g,h) и (b,d) в тензорном произведении соединены ребром, только если вершина g смежна с вершиной b в графе G и вершина h смежна с вершиной d в графе H.

Тензорное произведение графов

Если в исходных графах G и H ребер больше, чем вершин, то в их тензорном произведении больше ребер, чем в декартовом произведении. Казалось бы, чем больше ребер в графе, тем больше цветов нужно для его правильной раскраски. Однако нетрудно видеть, что для правильной раскраски тензорного произведения графов G и H достаточно использовать правильную раскраску любого из них.

Действительно, если покрасить каждую вершину (u,v) тензорного произведения в тот цвет, в который была покрашена вершина u графа G, то любая смежная с ней вершина (g,h) окажется покрашена в другой цвет, поскольку вершины u и g были смежны в графе G и его раскраска была правильной. Значит, цвета вершин (u,v) и (g,h), так же как вершин u и g, различны. Поэтому хроматическое число тензорного произведения не превосходит минимума хроматических чисел сомножителей.

Правильная раскраска тензорного произведения графов

Сильным произведением двух графов G₁ и G₂ называется граф с тем же множеством вершин, как у декартова и тензорного произведения этих графов. Ребрами сильного произведения графов являются одновременно ребра декартова и тензорного произведений.

Гипотеза Хидетниеми и ее опровержение

Естественно предположить, что хроматическое число тензорного произведения будет в точности равно минимуму хроматических чисел сомножителей. Ведь каждая вершина тензорного произведения графов имеет гораздо больше соседей, чем было у вершин исходных графов! Тем более что в похожем случае декартова произведения имеется равенство.

Это естественное предположение и сделал Хидетниеми. И оно подтверждалось практически для различных частных случаев, Например, граф на иллюстрации выше имеет циклы нечетной длины, а значит, его хроматическое число не меньше трех. И даже теоретически для некоторых классов графов было доказано, что гипотеза Хидетниеми верна, например для тензорного произведения любых двух графов с хроматическими числами не более 4.

Круг графов, для которых удалось проверить правильность гипотезы Хидетниеми постепенно расширялся и казалось, что вот-вот гипотеза будет доказана полностью.

Однако Ярославу Шитову неожиданно удалось доказать обратное. Причем не посредством построенного с помощью компьютера контрпримера, а полностью теоретически.

Для того чтобы кратко описать его доказательство, нам понадобится несколько определений. Во-первых, для произвольного графа H определим экспоненциальный граф E_s(H). Вершинами графа E_s(H) будут функции, действующие из множества вершин графа H в множество чисел <1, …, s>. Две функции f и g будем считать смежными, если они принимают различные значения на любых вершинах, смежных в графе H.

Нетрудно убедиться, что тензорное произведение графов H и E_s(H) можно правильно раскрасить в s цветов, независимо от хроматического числа графа H. Определим раскраску вершины (u,f) тензорного произведения равной f(u). Рассмотрим пару вершин (u,f) и (v,g) смежных в тензорном произведении графов. Тогда вершины u и v смежны в H, а вершины f и g смежны в E_s(H). Значит, по определению экспоненциального графа числа f(u) и g(v) не совпадают, то есть так определенная раскраска тензорного произведения в s цветов является правильной.

Теперь нужно найти подходящий граф H, чтобы хроматические числа графа H и его экспоненциального графа E_s (H) были строго больше s.

Классическая теорема Пала Эрдеша утверждает, что найдутся графы со сколь угодно большим хроматическим числом и сколь угодно большим обхватом (минимальным циклом).

Рассмотрим граф G с обхватом 10 и хроматическим числом 5. Полным графом K_q, или q-кликой, называется граф на q вершинах, все вершины которого попарно соединены ребрами.

Определим граф H как сильное произведение графов G и K_q. Граф H получается подстановкой q-клик во все вершины графа G, причем все вершины смежных q-клик попарно соединены ребрами. Отсюда нетрудно доказать, что хроматическое число сильного произведения графа G на q-клику будет иметь хроматическое число не меньше чем 5q.

Ярославу Шитову удалось доказать, что для достаточно больших q и s > 4,1q экспоненциальный граф E_s(H) имеет хроматическое число строго большее, чем s. Теперь достаточно выбрать такое s, что 5q > s > 4,1q и мы получаем, что оба сомножителя H и E_s(H) в тензорном произведении имеют хроматические числа больше, чем s, а их тензорное произведение имеет хроматическое число равное s, как было доказано выше. Таким образом, гипотеза Хидетниеми опровергнута.

Слово автору опровержения

Я не уверен, что у специалистов было единое мнение о том, верна ли гипотеза Хидетниеми: некоторые исследователи считали ее верной, но были и те, кто считал иначе. В пользу истинности гипотезы говорили случаи графов с хроматическим числом не больше четырех (подробнее); графов с большими кликами (подробнее здесь, здесь и здесь), графов и гиперграфов Кнезера (подробнее), а также аналог гипотезы Хидетниеми для дробных раскрасок. Тем не менее, аналогичное утверждение оказывается неверным для бесконечных графов: контрпример был найден еще в 1985 году.

Как и многие математические задачи и результаты, гипотеза Хидетниеми появилась и активно изучалась, как мне кажется, из чистого любопытства. Говорить о том, что из нее следовали какие-то важные выводы за пределами «чистой математики», которые теперь придется пересматривать, я бы не стал.

На языке гомоморфизмов гипотеза Хидетниеми звучит так: все полные графы являются мультипликативными (граф K называется мультипликативным, если существование гомоморфизма из тензорного произведения графов G и H в граф K влечет наличие гомоморфизма из G в K или гомоморфизма из H в K). Понятие мультипликативности активно обсуждается и для других графов, но ситуация с достаточно большими кликами стала ясна лишь теперь. Были еще и топологические следствия из гипотезы Хидетниеми, но, так как гипотеза не подтвердилась, они остаются открытыми проблемами.

Источник