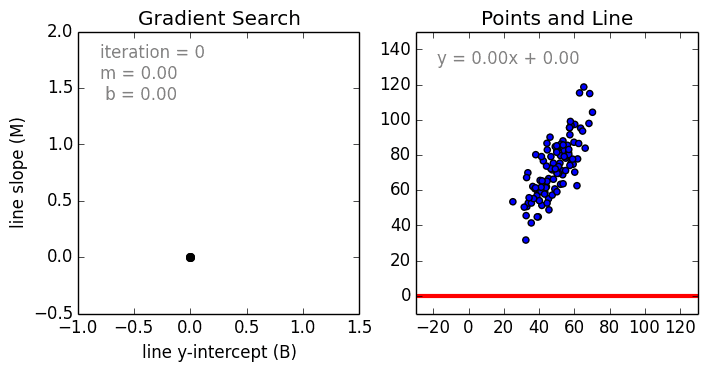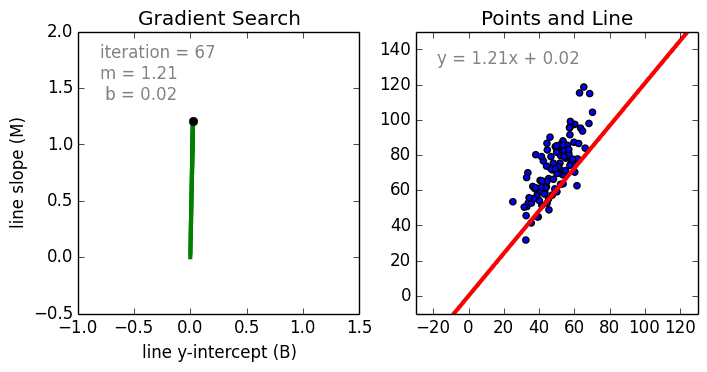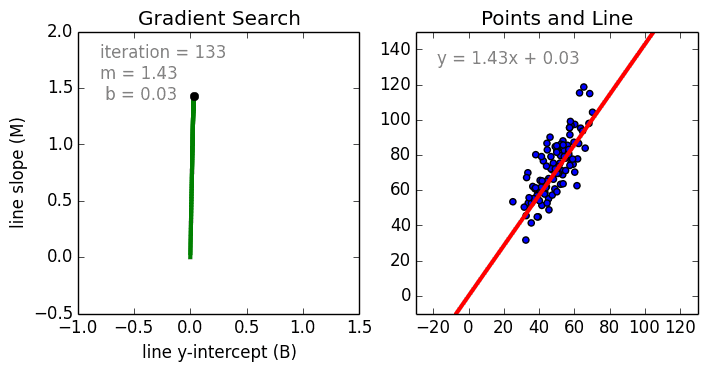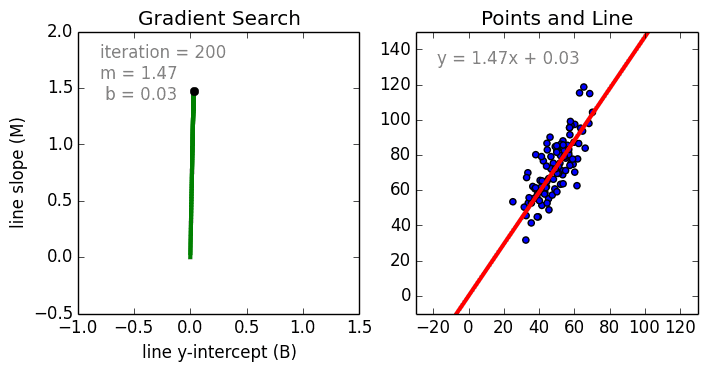
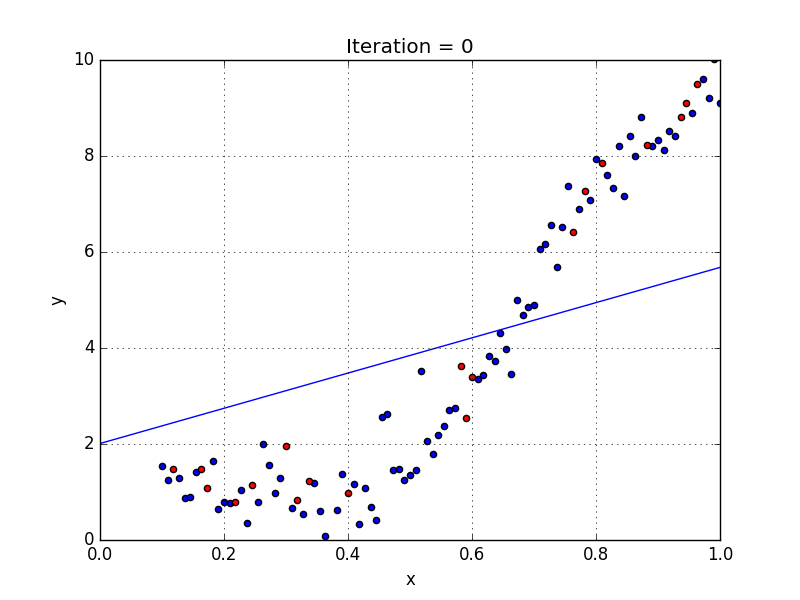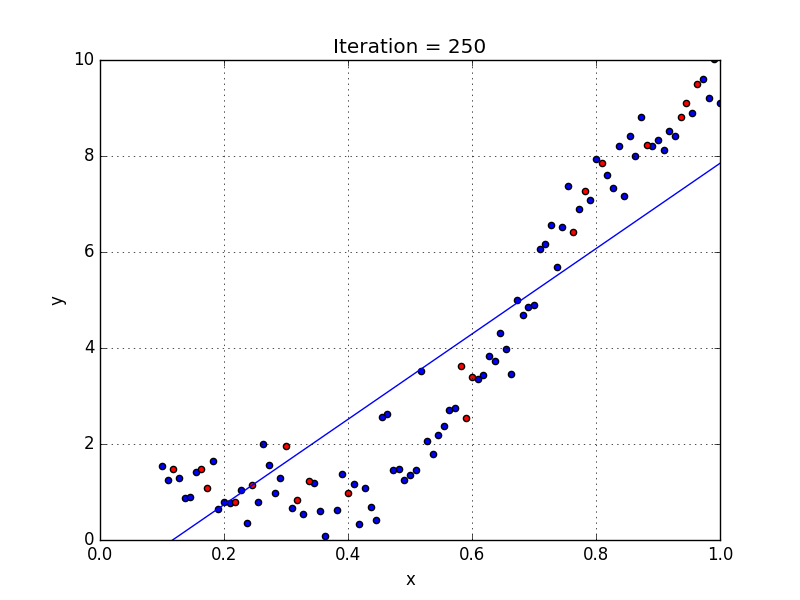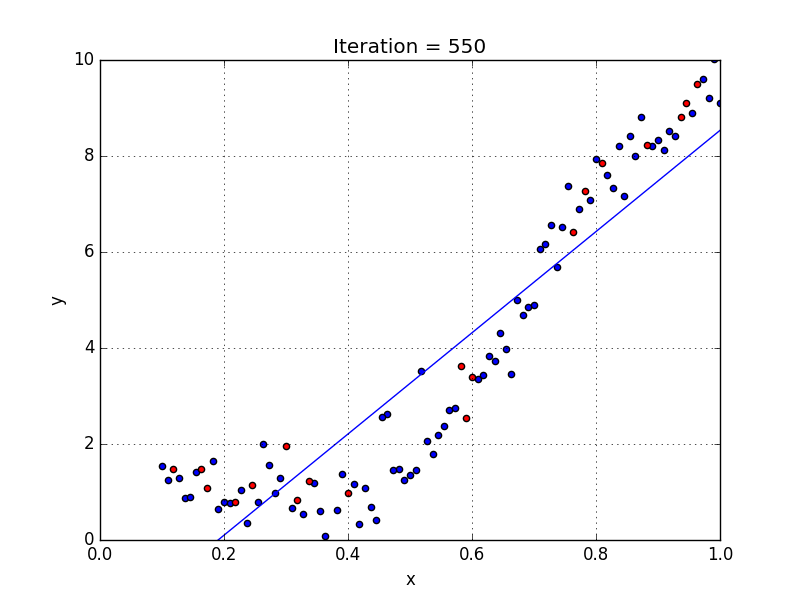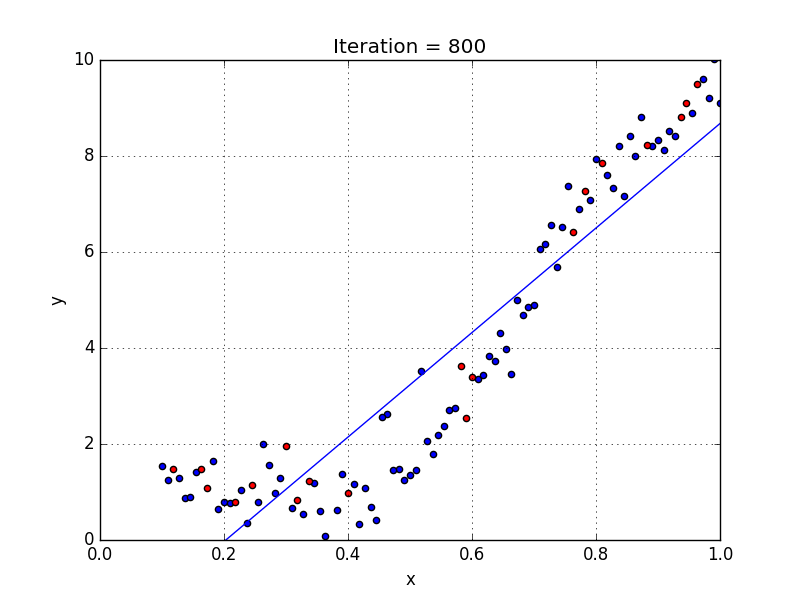
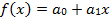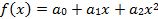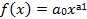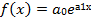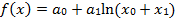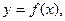что такое функция регрессии
Функция регрессии, стандартные модели функции регрессии. (25)



Функция регрессии – ожидаемое значение случайной переменной y, вычисленное при заданном значении переменной x.
Функция регрессии в эконометрике интерпретируется как выраженный математическим языком закон, по которому изменяется эндогенная переменная в ответ на изменения экзогенной переменной (без воздействия случайных возмущений).
Простейшие модели функции регрессии в эконометрике:
1) линейная функция
2) квадратичная функция
3) степенная функция
4) экспоненциальная (показательнаяыраженретируется как онометрикееменной, вычисленное при заданном значении переменной.в (МНК).
4) мо также подтвердить качество мод) функция
5) логарифмическая функция
В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.
Простая (парная) регрессия представляет собой регрессию между двумя переменными — у и х, т.е. модель вида:
где у — зависимая переменная (результативный признак);
х – независимая, или объясняющая, переменная (признак-фактор).
Примером модели парной регрессии является инвестиционная модель Самуэльсона-Хикса, имеет 2 переменных (It, ΔYt-1)
Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида:
R — значит регрессия
Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.
Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.
Введение в регрессионный анализ
Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей
минимальна.
Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.
Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений
вокруг регрессии
является дисперсия.
Линейная регрессия
Уравнения линейной регрессии можно записать в виде
В матричном виде это выгладит
Случайная величина может быть интерпретирована как сумма из двух слагаемых:
Ограничения линейной регрессии
Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.
Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.
Неоднородность дисперсии
При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.
Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.
Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.
В этой формуле — коэффициент взаимной детерминации между
и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.
Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.
Как преодолеть эти ограничения
Нарушения одной или нескольких ограничений еще не приговор.
К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.
Линейная регрессия плюсов на Хабре
Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.
Загружает данные из tsv файла.
Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.
В первой строке мы задаем параметры линейной регрессии. Строка points
. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points
Перейдем теперь к расшифровке полученных результатов.
Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.
Проверим значения параметров линейной регрессии.
Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.
И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.
В заключение
Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.
Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.
Основы анализа данных
Регрессионный анализ
Основная особенность регрессионного анализа: при его помощи можно получить конкретные сведения о том, какую форму и характер имеет зависимость между исследуемыми переменными.
Последовательность этапов регрессионного анализа
Рассмотрим кратко этапы регрессионного анализа.
Задачи регрессионного анализа
Установление формы зависимости.
Характер и форма зависимости между переменными могут образовывать следующие разновидности регрессии:
Однако описанные разновидности обычно встречаются не в чистом виде, а в сочетании друг с другом. В таком случае говорят о комбинированных формах регрессии.
Определение функции регрессии.
Вторая задача сводится к выяснению действия на зависимую переменную главных факторов или причин, при неизменных прочих равных условиях, и при условии исключения воздействия на зависимую переменную случайных элементов. Функция регрессии определяется в виде математического уравнения того или иного типа.
Оценка неизвестных значений зависимой переменной.
Решение этой задачи сводится к решению задачи одного из типов:
Обе задачи решаются путем подстановки в уравнение регрессии найденных оценок параметров значений независимых переменных. Результат решения уравнения представляет собой оценку значения целевой (зависимой) переменной.
Рассмотрим некоторые предположения, на которые опирается регрессионный анализ.
Предположение линейности, т.е. предполагается, что связь между рассматриваемыми переменными является линейной. Так, в рассматриваемом примере мы построили диаграмму рассеивания и смогли увидеть явную линейную связь. Если же на диаграмме рассеивания переменных мы видим явное отсутствие линейной связи, т.е. присутствует нелинейная связь, следует использовать нелинейные методы анализа.
При использовании регрессионного анализа следует учитывать его основное ограничение. Оно состоит в том, что регрессионный анализ позволяет обнаружить лишь зависимости, а не связи, лежащие в основе этих зависимостей.
Регрессионный анализ дает возможность оценить степень связи между переменными путем вычисления предполагаемого значения переменной на основании нескольких известных значений.
Уравнение регрессии выглядит следующим образом: Y=a+b*X
В большинстве случав (если не всегда) наблюдается определенный разброс наблюдений относительно регрессионной прямой.
| Регрессионная статистика | |
| Множественный R | 0,998364 |
| R-квадрат | 0,99673 |
| Нормированный R-квадрат | 0,996321 |
| Стандартная ошибка | 0,42405 |
| Наблюдения | 10 |
В большинстве случаев значение R-квадрат находится между этими значениями, называемыми экстремальными, т.е. между нулем и единицей.
В нашем примере мера определенности равна 0,99673, что говорит об очень хорошей подгонке регрессионной прямой к исходным данным.
Множественный R равен квадратному корню из коэффициента детерминации, эта величина принимает значения в интервале от нуля до единицы.
В простом линейном регрессионном анализе множественный R равен коэффициенту корреляции Пирсона. Действительно, множественный R в нашем случае равен коэффициенту корреляции Пирсона из предыдущего примера (0,998364).
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение | 2,694545455 | 0,33176878 | 8,121757129 |
| Переменная X 1 | 2,305454545 | 0,04668634 | 49,38177965 |
| * Приведен усеченный вариант расчетов | |||
Теперь рассмотрим среднюю часть расчетов, представленную в таблице 8.3б. Здесь даны коэффициент регрессии b (2,305454545) и смещение по оси ординат, т.е. константа a (2,694545455).
Исходя из расчетов, можем записать уравнение регрессии таким образом:
Направление связи между переменными определяется на основании знаков (отрицательный или положительный) коэффициентов регрессии (коэффициента b).
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
|---|---|---|---|
| 1 | 9,610909091 | -0,610909091 | -1,528044662 |
| 2 | 7,305454545 | -0,305454545 | -0,764022331 |
| 3 | 11,91636364 | 0,083636364 | 0,209196591 |
| 4 | 14,22181818 | 0,778181818 | 1,946437843 |
| 5 | 16,52727273 | 0,472727273 | 1,182415512 |
| 6 | 18,83272727 | 0,167272727 | 0,418393181 |
| 7 | 21,13818182 | -0,138181818 | -0,34562915 |
| 8 | 23,44363636 | -0,043636364 | -0,109146047 |
| 9 | 25,74909091 | -0,149090909 | -0,372915662 |
| 10 | 28,05454545 | -0,254545455 | -0,636685276 |
Следует учитывать, что рассматриваемый пример является достаточно простым и далеко не всегда возможно качественное построение регрессионной прямой линейного вида.
Осталась нерассмотренной задача оценки неизвестных будущих значений зависимой переменной на основании известных значений независимой переменной, т.е. задача прогнозирования.
Имея уравнение регрессии, задача прогнозирования сводится к решению уравнения Y= x*2,305454545+2,694545455 с известными значениями x. Результаты прогнозирования зависимой переменной Y на шесть шагов вперед представлены в таблице 8.4.
| x | Y(прогнозируемое) |
|---|---|
| 11 | 28,05455 |
| 12 | 30,36 |
| 13 | 32,66545 |
| 14 | 34,97091 |
| 15 | 37,27636 |
| 16 | 39,58182 |
Таким образом, в результате использования регрессионного анализа в пакете Microsoft Excel мы:
Если функция регрессии определена, интерпретирована и обоснована, и оценка точности регрессионного анализа соответствует требованиям, можно считать, что построенная модель и прогнозные значения обладают достаточной надежностью.
Прогнозные значения, полученные таким способом, являются средними значениями, которые можно ожидать.
Выводы
5 видов регрессии и их свойства
Jan 16, 2019 · 5 min read
Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.
Мы познакомимся с 7 наиболее распростран е нными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!
Линейная регрессия
Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.
Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:
Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b
Несколько важных пунктов о линейной регрессии:
Полиномиальная регрессия
Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:
Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b
У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.
Несколько важных пунктов о полиномиальной регрессии:
Гребневая (ридж) регрессия
В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:
Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:
Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.
Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:
Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.
Несколько важных пунктов о гребневой регрессии:
Регрессия по методу «лассо»
В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:
Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:
Регрессия «эластичная сеть»
Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.
min || Xw — y ||² + z_1|| w || + z_2|| w ||²
Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.
Несколько важных пунктов о регрессии эластичной сети:
Вывод
Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.