что такое фронтально проецирующая прямая

Фронтальная прямая

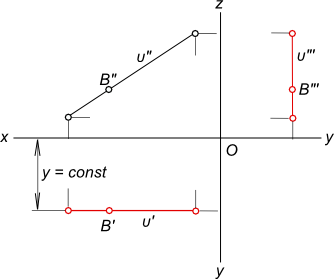
Приведенная запись означает: для множества точек B, принадлежащих прямой υ, ордината величина постоянная, характеризует удаление точек от фронтальной плоскости проекций.

Фронтальная прямая f –

Кроме общего случая, прямая по отношению к заданной системе плоскостей проекций может занимать частое положение. Прямые частного положения подразделяются на прямые уровня и проецирующие прямые.

Фронтальная прямая относится к частному случаю расположения прямой.

Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня. Существует три вида прямых уровня: горизонталь, Фронтальная прямая (фронталь) и профильная прямая.

К числу частных случаев расположения прямых можно отнести и прямые, лежащие непосредственно в плоскостях проекций. Их называют прямыми нулевого уровня.

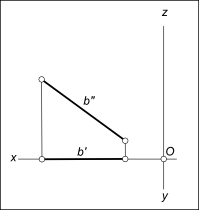
На рисунке приведен пример прямой нулевого уровня: фронталь f лежит во фронтальной плоскости проекций, а значит ее горизонтальные проекции на эпюре (КЧ) совпадают с осью O_x.

По расположению относительно плоскостей проекций бывают прямые частного положения: Горизонтальная прямая; Профильная прямая; Проецирующие прямые.

Источник

Прямая, параллельная плоскостям π₁ и π₃, т.е. перпендикулярная к π₂, называется фронтально-проецирующей. На рисунках 12, 13 изображен отрезок прямой KL_┴π₂.

Рис.12 Рис.13

У фронтально-проецирующей прямой проекцией на фронтальную плоскость будет являться точка. На горизонтальную и профильную плоскости проекций она спроецируется в отрезки, равные по длине самому отрезку прямой (K′ L′ = K′′′ L′′′ = [KL]).

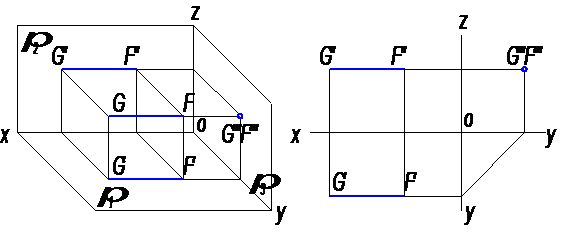
Прямая, параллельная плоскостям π₁ и π₂, т.е. перпендикулярная к π₃, называется профильно–проецирующей. На рисунках 14, 15 изображен отрезок прямой GF_┴π₃.

Рис. 14 Рис. 15

У профильно-проецирующей прямой проекция на профильную плоскость проекций представит собой точку. На горизонтальную и фронтальную плоскости она спроецируется в отрезки прямых, параллельных между собой и равных по длине самому отрезку (G′F′=G′′F′′=[GF]).

Прямые, параллельные двум плоскостям проекций и перпендикулярные к третьей называются проецирующими.

Прямые уровня и проецирующие называют прямыми частного положения.

Прямая общего положения

Прямая, непараллельная ни одной из плоскостей проекций, называется прямой общего положения. На рисунках 16, 17 изображен отрезок прямой ВС – общего положения.

У прямой общего положения ни одна из проекций не параллельна оси проекций и не перпендикулярна к ней. Каждая из проекций меньше самого отрезка, (В′С′

Точка на прямой

Если известно, что точка принадлежит прямой (например, точка С принадлежит прямой АВ), то горизонтальная проекция точки находится на горизонтальной проекции данной прямой, фронтальная проекция этой точки находится на фронтальной проекции прямой (рис. 18, 19).

Рис. 18 Рис. 19

На рисунке 20 показано построение точки на профильной прямой. Положим, что дана фронтальная проекция этой точки (С′′), надо найти ее горизонтальную проекцию (С′).

Построение горизонтальной проекции выполнено при помощи профильной проекции отрезка прямой АВ. Ход построения показан стрелками. Сначала определена профильная проекция точки С, а по ней найдена искомая проекция – С′ (рис. 20).

Одним из свойств параллельного проецирования является то, что отношение отрезков прямой линии равно отношению их проекций ( рис. 21).

Рис. 21

, так как прямые АА′, СС′, ВВ′ параллельны между собой. Аналогично отношение отрезков на проекции прямой линии равно отношению отрезков на этой прямой. Следует, что на рисунке 44 деление проекций А′′В′′ и А′В′ точками С′′ и С′ соответствует делению в пространстве отрезка прямой АВ точкой С в том же отношении.

На рисунке 46 показано деление отрезка прямой СD общего положения в отношении 2:5. Из точки С′ проведена вспомогательная прямая, на которой отложено семь отрезков произвольной длины, но равных между собой. Проведя отрезок D′7 и параллельно ему через точку 2 прямую, получаем точку К′, причем С′К′:К′Д′= 2:5; затем находим К′′.

Точка К делит отрезок СD в отношении 2:5 (рис. 22).

Источник

Проецирование прямой

Сообщение об ошибке

СОДЕРЖАНИЕ

Проецирование прямой

Прямая линия в пространстве определяется положением двух ее точек, например А и В, достаточно выполнить комплексный чертеж этих двух точек, затем соединить одноименные проекции, получим соответственно горизонтальную, фронтальную и профильную проекции прямой.

Проекция прямой – всегда прямая, кроме тех случаев, когда прямая перпендикулярна к одной из плоскостей, и проекция этой прямой на эту плоскость будет изображаться в виде точки.

Чтобы положение прямой в пространстве было определенным, необходимо иметь не менее двух проекций отрезка (рис.1).

Рис.1. Проекции прямой

Прямая общего положения – прямая, наклонная ко всем плоскостям проекций.

Прямая частного положения – прямая, параллельная хотя бы к одной из плоскостей проекций.

Условно частные положения прямых можно разбить на три группы.

Первая группа

Прямые параллельные двум плоскостям проекций и перпендикулярные к третьей.

Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций (рис.2).

Рис.2. Горизонтально проецирующая прямая

Фронтально проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций (рис.3).

Рис.3. Фронтально проецирующая прямая

Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций (рис.4).

Рис.4. Профильно проецирующая прямая

Вторая группа

Прямые параллельны одной плоскости проекций, а к двум другим направлены под углом.

Горизонтальная прямая – прямая, параллельная горизонтальной плоскости проекций (рис.5).

Рис.5. Горизонтальная прямая

Фронтальная прямая – прямая, параллельная фронтальной плоскости проекций (рис.6).

Рис.6. Фронтальная прямая

Профильная прямая – прямая, параллельная профильной плоскости проекций (рис.7).

Рис.7. Профильная прямая

Третья группа

Прямые, лежащие в плоскостях проекций (рис.8).

Рис.8. Прямая, лежащая в плоскостях проекций: а) в горизонтальной; б) в фронтальной; в) в профильной

Пример проецирования прямой

Построить недостающую проекцию прямой (рис.9).

Рис.9 Проецирование прямой

Для того, чтобы спроецировать прямую, необходимо спроецировать точки, принадлежащие этой прямой.

Находим точки пересечения координатных осей и проекционных линий (рис.10).

Рис.10 Проецирование прямой

Рис.11 Проецирование прямой

Соединяем проекционные линии из точек А_уП3 и А_z, а также В_уП3 и B_z (рис.12), получаем точки А′″ и B′″.

Рис.12 Проецирование прямой

Соединяем точки А′″ и B′″ и получаем третью проекцию прямой (рис.13).

Источник

Лекция 3. Плоскость

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

\left.\begin\alpha=m\parallel n,\\D\in\alpha\\C\in\alpha\\\end\right\> \Longrightarrow CD\in\alpha

Упражнение

Рисунок 3.7 – Решение задачи

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

\alpha=m\cap n\\\left.\begina_2\parallel m_2\\a_1\parallel m_1\\\end\right\> \Rightarrow a\parallel\alpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Упражнение

Алгоритм решения задачи :

\left.\beginAB\cap\sigma=K\\AC\cap\sigma=L\\\end\right\> \left.\begin\Rightarrow A_1B_1\cap\sigma_1=K_1 \rightarrow K_2\\\Rightarrow A_1C_1\cap \sigma_1=L_1 \rightarrow L_2\\\end\right.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

\left.\begin\alpha\cap\sigma=(4-5)\\\beta\cap\sigma=(3-2)\\\end\right\>\\\left.\begin\alpha\cap\tau=(6-7)\\\beta\cap\tau=(1-8)\\\end\right\>\left.\begin(4_1-5_1)\cap(3_1-2_1)=M_1\rightarrow M_2\\(6_1-7_1)\cap(1_1-8_1)=N_1\rightarrow N_2\\\end\right\>\rightarrow\\\left.\beginM_1N_1\\M_2N_2\\\end\right\>\Rightarrow\alpha\cap\beta=MN

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Источник