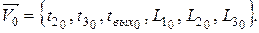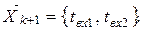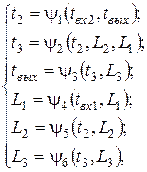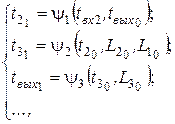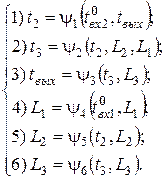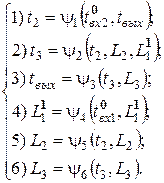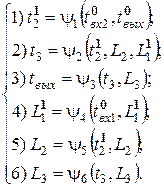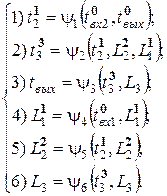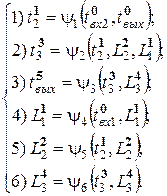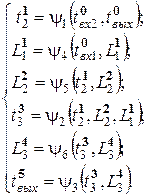что такое физическое время в имитационном моделировании
Три вида времени в имитационном моделировании



2. Системное или модельное время – это объект программы моделирования, имитирующий ход часов реального времени. Если реальная система функционирует на отрезке [t1,t2], то значение системного времени STIME тоже должно быть изменено в этих пределах, при выполнении условия STIME>t2 моделирования заканчивается
3. Компьютерное время – связано с продолжительностью выполнения программы моделирования, которое определяется эффективностью реализации программы и мощностью ресурсов компьютера.
Соотношение между различными типами времени
в имитационном моделировании
| Исследуемая система |
| Часы реального времени |
| Компьютер |
| Программа моделир-я |
| Часы модульного времени |
1
| Аппаратура |
| Таймер |
2
Связь 1 определяет отношение копирования, т.е. модельное время является копией реального.
Связь 2 определяет отношение управления. Таймер управляет выполнение программы моделирования.
Связь 3 определяет отношение синхронизации. Если связь 3 присутствует – это модель реального времени. Модельное время в компьютерном может только возрастать.
 компьютерное время компьютерное время |
 1 1 |
 2 2 |
| Эффект скачущих часов |
Эффект скачущих часов свидетельствует об ошибках в программе моделирования.
Величина 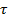
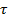
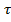
Методы пересчета модельного времени
Способы управления модельным временем
Дата добавления: 2015-06-12 ; просмотров: 2625 ; Нарушение авторских прав
Модельным временем в имитационной модели называется воспроизведение физического времени в модели. Соотношение физического и модельного времени определяется спецификой модели и задается диапазоном физического времени, принимаемого за единицу модельного времени. Сущностью имитационного моделирования является продвижение модельного времени и выполнение событий, связанных с определенными значениями модельного времени. Событие в модели это программный модельный образ значимого, с точки зрения разработчика модели, изменения в моделируемой системе.
Основной задачей имитационного моделирования является правильное отображение порядка и временных отношений между изменениями в моделируемой системе на порядок выполнения событий в модели.
Сжатие временной шкалы в непрерывном времени невозможно, поэтому в имитационном моделировании время изменяется скачкообразно. На оси модельного времени моменты наступления событий составляют дискретное множество. В дискретном имитационном моделировании используются два способа управления продвижением модельного времени:
— событийный (Event Driven), при котором в качестве следующего значения модельного времени выбирается минимальное время наступления события из списка будущих событий;
— пошаговый (Time Stepped), при котором значение модельного времени увеличивается на постоянную фиксированную величину – шаг модельного времени.
| ПРИМЕРЫ соотношения физического и модельного времени при пошаговом и событийном управлении. |  |
Пошаговый подход удобен при наличии условных событий, т. е. событий, для выполнения которых требуется истинность некоторого логического условия. В этом случае на каждом шаге требуется вычислять логические условия и выполнять соответствующие события. При событийном способе управления временем можно «проскочить» момент времени, при котором условие стало истинным.
Однако пошаговое управление значительно менее эффективно – для обеспечения удовлетворительной точности шаг приращения времени должен быть минимальным, а в этом случае »95% обращений к элементам имитационной модели – лишние и много процессорного времени тратится на обработку «пустых» интервалов. При этом пошаговое управление не позволяет указать истинное положение событий внутри шага модельного времени (такта). Поэтому принимается соглашение переносить их на начало (или на конец) того такта, в пределах которого они в действительности произошли. При этом искажается реальная картина событий, теряются причинно-следственные связи, последовательно протекающие события становятся параллельными, задержки распространения сигналов в структурных элементах не отображаются. Этих недостатков лишено событийное управление модельным временем [2, 29].
3.4.3. Алгоритмы имитационного моделирования для
событийного управления модельным временем
Отличие имитационного моделирования от объектно-ориентированного программирования заключается в том, что объект имитационной модели может не только выполнить некоторое событие в момент своей активности, но и запланировать выполнение своего события или события другого объекта в будущем, т. е. на момент модельного времени, больший или равный текущему значению модельного времени. Для реализации выполнения будущих событий и упорядочивания их в хронологическом порядке необходимо использование управляющей программы – планировщика. Алгоритм работы планировщика состоит в выполнении следующих действий:
1) активизация объектов для выполнения событий, запланированных на текущее значение модельного времени и удаление выполненных событий из списка;
2) включение в список новых событий, запланированных активными объектами, вместе со значениями моментов модельного времени, в которые каждое из этих событий должно быть выполнено;
3) увеличение значения модельного времени, если на текущий момент времени невыполненных событий не осталось, и переход на п.1).
Понятно, что при такой организации моделирования события в модели выполняются последовательно, даже если они относятся к одному моменту модельного времени. Однако, поскольку продвижение модельного времени на время моделирования параллельных событий приостанавливается, говорят, что процессы выполняются квазипараллельно.
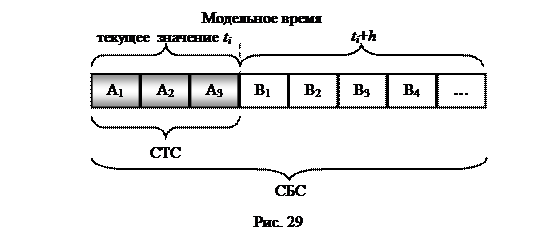
В алгоритме имитационного моделирования СМО при событийном управлении модельным временем используется несколько информационных массивов: списки текущих (СТС) и будущих (СБС) событий, массив заявок (МЗ) – хранит имя, тип, приоритет, время, местонахождение заявки в системе, и очередей (МО) – хранит информацию о заявках в очереди, упорядочен по ОА. Моделирование начинается с просмотра операторов генерирования заявок, т. е. с обращений к моделям источников заявок. Для каждого независимого источника такое обращение позволяет рассчитать момент генерации первой заявки. Этот момент вместе с ссылкой на заявку заносится в СБС, а сведения о заявке – в МЗ (имя, значения параметров, место появления или нахождения заявки в системе). В СБС события упорядочиваются по возрастанию времен совершения. Далее из СБС выбирается совокупность событий, относящихся к наиболее раннему моменту модельного времени. Эта совокупность переносится в СТС и начинается моделирование событий, отмеченных в СТС (см. рис. 29).
Выбирается ссылка на событие, по ней в МЗ определяется соответствующая заявка и ее место в системе, моделируется продвижение по системе по маршруту, определяемому программой моделирования, до тех пор, пока заявка не придет на вход некоторого ОА. Тогда обращение к модели ОА позволяет определить длительность задержки на обслуживание и момент наступления события, связанного в выходом заявки из ОА. Корректируется местонахождение заявки в МЗ. Ссылка на новое предвидимое событие заносится в СБС так, чтобы сохранилась упорядоченность списка по моментам наступления событий. Программа моделирования приступает к выбору очередной ссылки на СТС.
После имитации всех событий из СТС в него переносится очередная совокупность событий из СБС, относящихся к ближайшему моменту модельного времени ti+1, текущее модельное время принимает это значение.
Если при моделировании движения заявки она придет на вход занятого ОА (устройства или накопителя), то вместо расчета длительности обслуживания имя заявки заносится в МО. При моделировании события, связанного с освобождением ОА заявкой а, проверяется состояние очереди к освобождающемуся ОА. Если имеется очередь, то в соответствии с дисциплиной обслуживания из очереди выбирается заявка b и входит на обслуживание ОА. Обращение к модели обслуживающего аппарата дает значение освобождения ОА заявкой b и соответствующая ссылка заносится в СБС. Затем программа производит моделирование продвижения заявки a до того момента, когда произойдет ее выход из системы или задержка в очереди к новому ОА [1, 28, 29].
3.4.4. Алгоритмы имитационного моделирования для
пошагового управления модельным временем
При пошаговом управлении модельным временем трудоемкость анализа имитационной модели определяется количеством уравнений в итоговой системе и количеством тактов, на которое разделен моделируемый интервал времени. Для моделирования в этом случае используются итерационные алгоритмы функционального моделирования дискретных систем.
Для решения систем уравнений вида V=y(V,X), где V – вектор базисных переменных; X – вектор входных переменных модели; y – оператор преобразования дискретных переменных, применяются итерационные алгоритмы. Анализ начинается с задания вектора входных воздействий X и вектора начального приближения V0 для искомого вектора V.
| ПРИМЕРЫ синхронного анализа логической схемы с использованием итерационных алгоритмов. |  |
Алгоритм простой итерации состоит в выполнении итераций по следующей формуле:
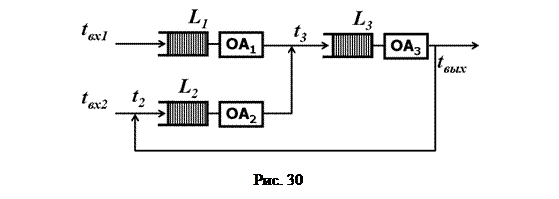
Рассмотрим постановку задачи моделирования СМО с ОА типа G/G/1 (см. рис. 30) для пошагового управления модельным временем.
Вектор входных переменных модели для СМО, представленной на рис. 30, имеет вид:
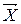
где tвх1 и tвх2 – время поступления заявок входных потоков на обслуживание в очередь ОА1 и ОА2 соответственно. Вектор базисных координат может быть определен как:
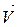
где t2 – время поступления заявки из рецикла на повторное обслуживание в очередь ОА2; t3 – время поступления заявки на обслуживание в очередь ОА3; tвых – время выхода заявки из системы; L1, L2, L3 – длины очередей соответствующих ОА.
Пусть на k-тый момент модельного времени значение вектора базисных координат известно и может быть использовано в качестве начального приближения для расчетов в следующем такте модельного времени:
Пусть в k+1 момент модельного времени значение вектора входных переменных составило:
Требуется определить значение вектора базисных координат 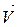
где yi – функции, зависящие от закона распределения времени обслуживания в АО и дисциплины очереди.
Согласно формуле (10) в правые части уравнений модели на каждой итерации в этом алгоритме подставляются значения базисных координат, полученных на предыдущей итерации. На первой итерации такими значениями являются значения базисных координат из начального приближения вектора, следовательно:
и так далее. Следует обратить внимание, что, например, для расчета базисной координаты 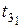
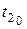
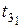
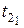
Признаком того, что решение найдено, в этом итерационном метода, как и во всех прочих, является совпадение результата последней итерации с предыдущей.
Уменьшить количество вычислений удается при построении итерационного процесса с использованием алгоритма Зейделя, в котором при вычислении очередного из элементов вектора Vi в правую часть уравнений системы там, где это возможно, подставляются не элементы вектора Vi-1, а те элементы вектора Vi, которые уже вычислены к данному моменту, т. е. итерации выполняются по формуле:
Количество итераций в алгоритме Зейделя существенно зависит от порядка, в котором реализуются уравнения модели. В алгоритме Зейделя без ранжирования уравнения модели перечисляются в произвольном порядке. В алгоритме Зейделя с ранжированием уравнения располагаются в том порядке, в каком соответствующие уравнениям элементы схемы образуют путь прохождения заявок. Тогда для анализа схем без обратных связей потребуется всего одна итерация. В схемах с обратной связью метод Зейделя с ранжированием уравнений порождает несколько итераций, но их количество существенно меньше, чем в методе простой итерации.
Ранжирование уравнений производится следующим образом: уравнение модели (элемент СМО) получает ранг j, если все аргументы этого уравнения (входы элемента) ранжированы и максимальный среди рангов аргументов (входов) равен j-1. Переменная модели получает ранг j, если она является левой частью уравнения (является выходом элемента), имеющего ранг j. Выполнение алгоритма начинается с того, что всем входным переменным присваивается ранг j=0. Если в схеме имеются контуры ОС, одна из цепей каждого контура должна быть предварительно разорвана и части разорванных цепей, подключенные к входам элементов, получают ранг j=0. Затем определяют уравнения первого ранга, переменные первого ранга, элементы второго ранга и т. д. В итоге уравнения располагаются в порядке возрастания рангов.
Выполним ранжирование уравнений системы, описывающей СМО, приведенную на рис. 30 и рассмотренную выше, в примере моделирования по методу простой итерации. Присвоим нулевой ранг входным переменным:
Как видно, в четвертом уравнении теперь фигурирует единственная непроранжированная переменная: L1, которая фигурирует и в правой, и в левой части. Ей присваивается ранг, на 1 больший минимального в уравнении, т. е. в данном случае равный 1. Этим же рангом помечаются все вхождения переменной L1 в другие уравнения:
Как видно, после выполнения последнего шага дальнейшее ранжирование становиться невозможным без условного разрыва обратной связи. Условный разрыв позволяет отнести переменную tвых к нулевому рангу. В результате в первом уравнении все переменные в правой части оказываются проранжированными, поэтому t2 в этом уравнении, а также в правых частях второго и пятого уравнений, получает ранг 1:
В пятом уравнении теперь фигурирует единственная непроранжированная переменная: L2, которая фигурирует и в правой, и в левой части. Ей присваивается ранг, на 1 больший минимального в уравнении, т. е. в данном случае равный 2. Этим же рангом помечаются все вхождения переменной L2 в другие уравнения, что позволяет определить ранг переменной t3 равным 3. С учетом вхождений этой переменной получим:
В шестом уравнении теперь фигурирует единственная непроранжированная переменная: L3, которая фигурирует и в правой, и в левой части. Ей присваивается ранг, на 1 больший минимального в уравнении, т. е. в данном случае равный 4. Этим же рангом помечаются вхождение переменной L3 в третье уравнение, что позволяет определить действительный (без условного разрыва обратной связи) ранг переменной tвых равным 5. Окончательный результат ранжирования имеет вид:
Расположим уравнения по возрастанию рангов:
Если сопоставить ранжированный порядок уравнений со схемой на рис. 30, легко убедиться, что порядок вычислений в этом случае соответствует логике прохождения заявок по СМО и порядку изменения переменных модели. Понятно, что для такой простой схемы расположить уравнения в правильном порядке можно и без процедуры ранжирования. Однако в сложных схемах с большим количеством ОА и обратных связей эта задача не тривиальна, и приходиться прибегать к ранжированию.
Наименьший объем вычислений обеспечивает событийный алгоритм. Основная идея событийного метода заключается в выполнении вычислений по уравнениям только активизированных элементов, т. е. элементов, у которых хотя бы на одном входе произошло событие (изменилась входная переменная). В алгоритме событийного метода на каждой итерации имеется своя группа активизированных элементов. Использование метода позволяет существенно сократить затраты машинного времени при анализе имитационных моделей СМО [3, 10, 29].
Представление времени в процессе имитации
При имитационном моделировании выделяют три представления времени: реальное, модельное (системное) и машинное время.
Реальное время – это время, в котором происходит функционирование моделируемой системы в реальной жизни, например час, смена, год.
Модельное (системное) время – это время, в котором происходит функционирование моделируемой системы при проведении имитационного моделирования
на ЭВМ. В системном времени выполняются следующие действия:
• осуществляется переход моделируемой системы из одного состояния в другое;
• выполняется синхронизация работы всех компонент имитационной модели;
• обеспечивается управление ходом имитационных экспериментов;
• обеспечивается параллельная реализация событий в моделируемой системе.
Машинное время – это время, отражающее затраты времени ЭВМ на проведение имитационного моделирования.
Система моделирования GPSSW основана на переходе требований (транзактов) от блока к блоку (от оператора к оператору) в определенные моменты времени, что называется событием.
Событие – это нечто, меняющее статус связанных с ним состояний системы.
События соответствуют конкретным изменениям в реальной системе: требование
появилось, требование вошло в очередь, требование обслуживается и т.д. При этом
прослеживается процесс моделирования с использованием как абсолютного времени (текущего), так и относительного (с начала прогона модели, с момента последней модификации или последнего сброса и т.д.). События характеризуются
условиями (или законом) возникновения и типом, который определяет порядок
их обработки (дисциплину обслуживания). Событие по существу представляет
собой мгновенное изменение некоторого элемента системы или состояния системы в целом. Очень важная особенность GPSSW заключается в том, что продолжительность
моделирования определяется не длительностью интервалов между событиями,
а числом событий, возникающих в системе. Поэтому переход на более мелкие единицы времени не увеличивает время моделирования.
Дата добавления: 2015-10-13 ; просмотров: 2497 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Лекция 6. Механизмы продвижения модельного времени
Лекция 6. Механизмы продвижения модельного времени
Реальные объекты являются динамическими системами. Они функционируют во времени, в них протекают определённые процессы, которые можно представить чередой сменяющих друг друга состояний. Время является непременным атрибутом таких систем и, следовательно, его надо уметь моделировать наряду с другими параметрами.
При моделировании реальные параметры объекта заменяются модельными. Это касается и реального времени tр: в ходе моделирования оно представляется некоторым искусственным (системным) временем, которое обычно называют модельным временем, и обозначают tm..
Существуют два классических способа продвижения модельного времени: «принцип Dt» и «принцип dz».
Рассмотрим их особенности на конкретном примере, показанном на рис.1.
Принцип Dt весьма прост. Ось времени разбивается на равные временные интервалы (такты) длительностью Dt. Следовательно, модельное время может принимать только дискретные значения, кратные этому временному интервалу: Dt, 2Dt, 3Dt и так далее. Моделирующая программа (моделятор) продвигает модельное время в соответствии с формулой:
В начале моделирования этот счётчик сбрасывается в нулевое состояние (T:=0), а затем его содержимое увеличивается на «1» с каждым циклом работы моделятора: (T := T+1). Таким образом, переменная T показывает текущее модельное время, которое движется скачками одинаковой длины Dt (подобно секундной стрелке на часах) от «0» до Tmax. Величина Tmax задаётся пользователем и определяет конечное время моделирования.
Длительность такта Dt также является прерогативой пользователя и для синхронных цифровых устройств обычно составляет половину периода синхронизации.
Разрешённые временные отметки никак не привязаны к моментам появления реальных событий в объекте, поэтому последние приходится искусственно передвигать на границы тактов, вынужденно искажая реальную картину. На рис.1 показано, что каждое реальное событие «привязываются» к левой границе того такта, в пределах которого оно в действительности произошло. Понятно, что принятое соглашение может быть другим: реальное событие с тем же успехом можно перенести на конец того такта, в котором это событие произошло.
Основное (а, возможно, и единственное) достоинство принципа Dt заключается в простоте его машинной реализации. Про недостатки следует поговорить подробнее.
Принцип Dt не позволяет указать истинное положение событий внутри интервала Dt. Поэтому принимается соглашение переносить их на начало (или на конец) того такта, в пределах которого они в действительности произошли. При этом искажается реальная картина событий, теряются причинно-следственные связи, последовательно протекающие события становятся параллельными, задержки распространения сигналов в структурных элементах не отображаются.
Много процессорного времени тратится на обработку «пустых» интервалов (рис.1). Их число резко возрастает при попытке более точно смоделировать реальные события, так как для этого надо уменьшать длительность такта Dt.
Такая модель, ориентированная на события, должна функционировать в неравномерной шкале модельного времени, «перепрыгивая» от одного события к другому. При этом стрелка модельных часов перемещается от текущего события к ближайшему будущему, не останавливаясь в промежутках между ними.
Моделятор имитирует реакцию объекта на событие E1, что может привести к появлению новых событий. Затем модельное время передвигается на ближайшее следующее событие E2 (tm := tm2) и цикл работы моделятора повторяется вновь. Понятно, что «расстояние» между соседними событиями может быть произвольным, поэтому шкала модельного времени получается неравномерной.
Таким образом, модельное время, продвигаемое по принципу dz, определяется по простой формуле:
tm := tm + Dtближ , если время вычисляется в относительных единицах.
Результаты сравнения рассмотренных принципов управления модельным временем приведены в таблице 1.
Модельное время не «привязано» к реальным событиям. Оно движется само по себе, не обращая внимания на происходящие в объекте процессы.
Модельное время «опирается» на события, то есть временные отметки «привязаны» к моментам наступления реальных событий.
Шкала модельного времени tm равномерна. Время движется шагами одинаковой длины Dt :
Шкала модельного времени tm не равномерна. Время движется скачками разной длины, равной «расстоянию» между соседними событиями:
Моменты появления событий при моделировании не искажаются.
Так как время наступления события фактически округляется до длительности такта Dt, то возникает систематическая погрешность метода, которая может достигать величины Dt.
Время наступления событий не приходится округлять до значения, кратного Dt. Точность моделирования выше.
Нарушаются причинно-следственные связи.
Не нарушаются причинно-следственные связи.
Последовательные события в пределах одного такта неразличимы и будут отображаться как одновременные.
Адекватность воспроизведения последовательных событий не искажается, как бы близко друг к другу они не находились.
Временные задержки в структурных элементах не воспроизводятся.
Временные задержки в структурных элементах моделируются естественным образом.
Непроизводительно (вхолостую) тратится машинное время на обработку «пустых» тактов.
«Холостые» циклы работы моделятора отсутствуют. Эффективность алгоритма гораздо выше.
На рис.2 показана последовательность действий при подготовке реальных сигналов для моделирования по принципу Dt. Сначала ось времени разбивается на одинаковые интервалы длительностью Dt. Сверху эта длительность ограничена одним совершенно необходимым условием: в пределах такта любой сигнал должен переключаться не более одного раза. В противном случае фронт и спад сигнала будут перенесены на начало одного и того же такта, и длительность импульса станет равной нулю.
На рис.2,а показаны временные диаграммы работы двоичного суммирующего счётчика с последовательным переносом. Входной сигнал CLOCK поступает на вход счётчика, который находился в состоянии «7» (Q1=Q2=Q3=1, Q4=0).
Счётчик должен переключиться в состояние «8» (Q1=Q2=Q3=0, Q4=1). При последовательном переносе один триггер управляет другим и на временных диаграммах отчётливо видны задержки при смене состояния каждого триггера. Причинно-следственные связи для наглядности показаны пунктирными стрелками. Триггеры срабатывают один за другим, начиная с младшего разряда счётчика.
При моделировании длительности фронтов и спадов сигналов игнорируются, и они представляются мгновенными событиями C1. C9 (рис.2,б). Задержки распространения сигналов в элементах представляются чистыми задержками, и, к сожалению, при моделировании по принципу Dt воспроизводиться не будут, потому что все переключения в пределах такта будут перенесены на его начало (рис.2,в). Последовательные события становятся параллельными и причинно-следственные связи теряются.
Реальное, модельное и машинное времена
Реальные динамические системы (объекты) работают в реальном (физическом) времени, которое обозначают буквой tp. При моделировании они замещаются некоторыми другими системами, называемыми имитационными моделями. Процессы, протекающие в таких моделях, должны адекватно отображать поведение моделируемых объектов: если события в реальной системе совпадают, то они должны совпадать и в модели, если реальные события следуют в определённом порядке, то он не должен нарушаться и в модели.
Можно допустить (и это действительно имеет дело на практике) проведение имитационных экспериментов в реальном масштабе времени, однако чаще процессы в имитационных моделях развиваются в некотором другом, искусственном времени. Оно называется системным или модельным временем и обозначается через tm. Это время существует только в ходе экспериментов с имитационной моделью, то есть при её прогонах. В отличие от реального модельным временем можно управлять: его легко остановить, вернуть на начальное значение, пройти некоторые отрезки времени многократно, двигаясь при этом равномерно или скачками разной длины.
В цифровых ЭВМ переменная tm может быть представлена только как дискретная величина. В этом случае необходимо выбрать единицу дискретного времени. Её обозначают через Dt и называют квантом времени (временным шагом). Фактически это разрешающая способность по времени при моделировании: последовательные события, «расстояние» между которыми меньше Dt, будут восприниматься как одновременные.
Замедление модельного эксперимента относительно реального времени объясняется тем, что чаще всего в качестве инструментальной ЭВМ выступает однопроцессорная система. Это означает, что в любой момент машинного времени может обрабатываться только одно событие. Если в моделируемом объекте развиваются параллельные процессы, то их приходится обрабатывать по очереди. И чем больше одновременных (кратных) событий, тем медленнее выполняется моделирование.
Чтобы не нарушалась хронологическая последовательность событий в моделируемом объекте, надо иметь какой-нибудь механизм имитации параллельных процессов. Обычно это делается так: модельное время останавливается («замораживается») до тех пор, пока одно за другим не будут обработаны все кратные события. Такой механизм называют псевдопараллельной обработкой, потому что процессы протекают параллельно в модельном времени (оно остановлено) и обрабатываются последовательно в машинном времени. При этом события в модельном времени отображаются как мгновенные (они обозначаются точкой на оси времени tm), тогда как в машинном времени они конечны (моделирование реакции системы на событие требует определённого процессорного времени).
Связь между модельным tm и машинным tэвм временами представлена в графическом виде на рис.3.
 |
Допустим, в реальной динамической системе развиваются два параллельно протекающих процесса. Один процесс может останавливать или запускать другой. Причинно-следственные связи между событиями показаны пунктирными стрелками.
Перед началом моделирования составляется календарь (очередь) будущих событий, в котором все события сортируются в хронологическом порядке. Счётчик модельного времени (модельные часы) устанавливается в «0» и запускается моделятор.
Он выбирает из очереди будущих событий ближайшее (на рис.3 это событие D1) и устанавливает модельные часы на время свершения (наступления) выбранного события (tm := tD1). Моделируется реакция системы на событие D1. При этом могут появиться новые события, которые моделятор должен включить в календарь событий, соблюдая хронологический порядок. На обработку события D1 будет затрачено определённое машинное время.
Таким образом, при обработке события D1 модельное время фиксировано (событие в модельном времени мгновенно), а по координате tэвм рабочая точка непрерывно перемещается, пока не закончится обработка реакции объекта на событие D1. После этого модельное время «оживает» («размораживается») и моделятор передвигает стрелку модельных часов на ближайшее следующее событие (на рис.3 это событие C1): tm := tC1.
Кратные (одновременные) события, например C2 и D2 на рис.3, обрабатываются моделятором похожим образом. Модельное время останавливается, пока не будет обработан весь список кратных событий.
Заметим, что последовательность их обработки не влияет на результат, потому что изменение состояния системы от каждого такого события произойдёт не в текущий момент модельного времени, а с задержкой, вызванной инерционностью реальных объектов. Другими словами, это случится не в текущем, а в последующих циклах работы моделятора.
Единственное условие, которое необходимо выполнить в данной ситуации – сначала сменить все старые значения на новые в точках, где обнаружены кратные события, а уже затем приступить к их обработке.