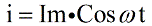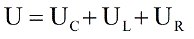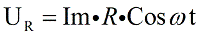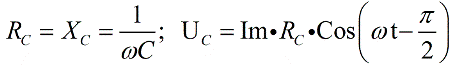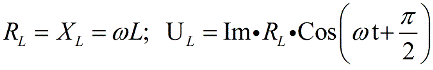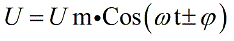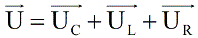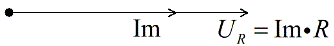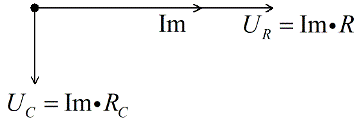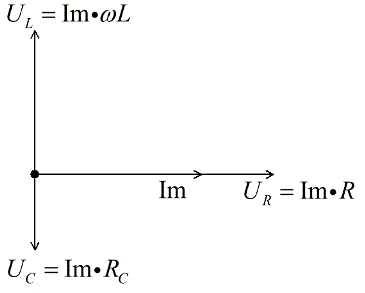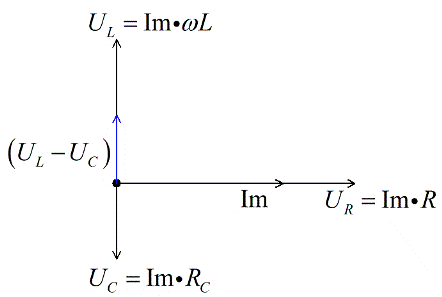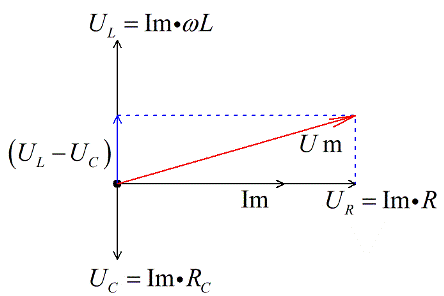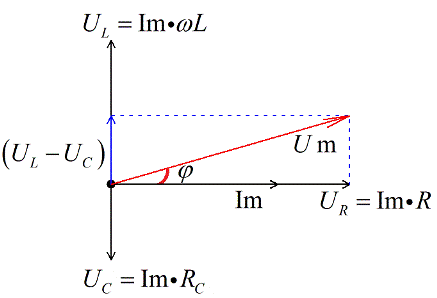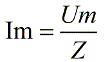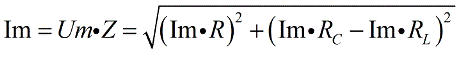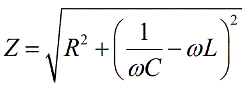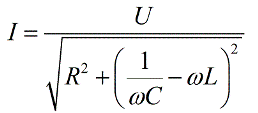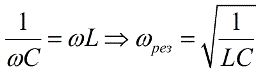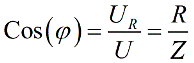что такое фазовый вектор
Как построить векторную диаграмму токов и напряжений
Векторные диаграммы — метод графического расчета напряжений и токов в цепях переменного тока, в которых переменные напряжения и токи символически (условно) изображаются с помощью векторов.
Поэтому всякое переменное напряжение (или переменный ток), меняющееся по синусоидальному закону, можно изображать с помощью такого вектора, вращающегося с угловой скоростью, равной угловой частоте изображаемого тока, причем длина вектора в определенном масштабе изображает амплитуду напряжения, а угол — начальную фазу этого напряжения.
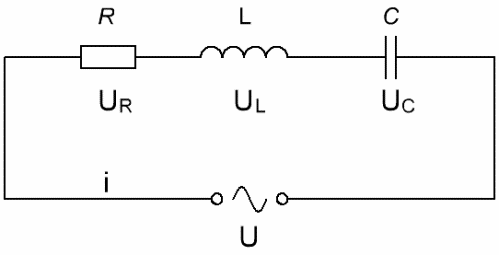
Если рассмотреть электрическую цепь, состоящую из последовательно соединенных источника переменного тока, резистора, индуктивности и конденсатора, где U – мгновенное значение переменного напряжения, а i – это ток в текущий момент времени, причем U изменяется по синусоидальному (косинусоидальному) закону, то для тока можно записать:
Согласно закону сохранения заряда, в любой момент времени ток в цепи имеет одно и то же значение. Следовательно на каждом элементе будет падать напряжение: UR– на активном сопротивлении, UC – на конденсаторе, и UL – на индуктивности. Согласно второму правилу Кирхгофа, напряжение источника будет равно сумме падений напряжений на элементах цепи, и мы имеем право записать:
Заметим, что согласно закону Ома: I = U/R, и тогда U = I*R. Для активного сопротивления значение R определяется исключительно свойствами проводника, оно не зависит ни от тока, ни от момента времени, следовательно ток совпадает по фазе с напряжением, и можно записать:
Можно записать теперь сумму падений напряжений, но в общем виде для приложенного к цепи напряжения можно записать:
Видно, что здесь имеет место некий сдвиг фаз, связанный с реактивной составляющей общего сопротивления цепи при протекании по ней переменного тока.
Поскольку в цепях переменного тока и ток и напряжение изменяются по закону косинуса, причем мгновенные значения отличаются между собой лишь фазой, то физики придумали в математических расчетах рассматривать токи и напряжения в цепях переменного тока как векторы, поскольку тригонометрические функции можно описать через векторы. Итак, запишем напряжения в виде векторов:
Используя метод векторных диаграмм, можно вывести, например, закон Ома для данной последовательной цепи в условиях протекания по ней переменного тока.
Согласно закону сохранения электрического заряда, в любой момент времени ток во всех частях данной цепи одинаков, так отложим же векторы токов, построим векторную диаграмму токов:
Пусть в направлении оси Х будет отложен ток Im – амплитудное значение тока в цепи. Напряжение на активном сопротивлении совпадает по фазе с током, значит эти векторы будут сонаправленными, отложим их из одной точки.
Напряжение на конденсаторе отстает на Пи/2 от тока, следовательно откладываем его под прямым углом вниз, перпендикулярно вектору напряжения на активном сопротивлении.
Напряжение на катушке опережает на Пи /2 ток, следовательно откладываем его под прямым углом вверх, перпендикулярно вектору напряжения на активном сопротивлении. Допустим, что для нашего примера UL>UC.
Поскольку мы имеем дело с векторным уравнением, сложим векторы напряжений на реактивных элементах, и получим разницу. Она будет для нашего примера (мы приняли что UL>UC) направлена вверх.
Прибавим теперь вектор напряжения на активном сопротивлении, и получим, по правилу векторного сложения, вектор суммарного напряжения. Так как брали максимальные значения, то и получим вектор амплитудного значения общего напряжения.
Так как ток менялся по закону косинуса, то напряжение тоже меняется по закону косинуса, но со сдвигом фаз. Между током и напряжением есть постоянный сдвиг фаз.
Запишем закон Ома для общего сопротивления Z (импеданса):
Из векторных изображений по Теореме Пифагора можем записать:
После элементарных преобразований получим выражение для полного сопротивления Z цепи переменного тока, состоящей из R, C и L:
Тогда получим выражение для закона Ома для цепи переменного тока:
Заметим, что наибольшее значение тока получатся в цепи при резонансе в условиях, когда:
Косинус фи из наших геометрических построений получается:
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
СОДЕРЖАНИЕ
Обозначение
Определение
Формула Эйлера показывает, что синусоиды могут быть представлены математически как сумма двух комплекснозначных функций:
или как реальная часть одной из функций:
Арифметика
Умножение на константу (скаляр)
Добавление
Сумма нескольких векторов дает еще один вектор. Это потому, что сумма синусоид с одинаковой частотой также является синусоидой с этой частотой:
Другими словами, это показывает, что
Поскольку единственный вектор вращается против часовой стрелки, его вершина в точке A совершит один полный оборот на 360 ° или 2 π радиан, представляющих один полный цикл. Если длина его движущегося наконечника переносится с разными угловыми интервалами во времени на график, как показано выше, синусоидальная форма волны будет нарисована, начиная слева с нулевого времени. Каждая позиция по горизонтальной оси указывает время, прошедшее с момента нуля, t = 0. Когда вектор расположен горизонтально, вершина вектора представляет углы в 0 °, 180 ° и 360 °.
Иногда, когда мы анализируем чередующиеся формы сигналов, нам может потребоваться знать положение фазора, представляющего переменную величину в некоторый конкретный момент времени, особенно когда мы хотим сравнить две разные формы сигналов на одной оси. Например, напряжение и ток. В приведенной выше форме волны мы предположили, что она начинается в момент времени t = 0 с соответствующим фазовым углом в градусах или радианах.
Дифференциация и интеграция
Производная по времени или интеграл фазора дает другой вектор. Например:
Когда мы решаем линейное дифференциальное уравнение с помощью векторной арифметики, мы просто вычитаем все члены уравнения и снова вставляем их в ответ. Например, рассмотрим следующее дифференциальное уравнение для напряжения на конденсаторе в RC-цепи : е я ω т <\ Displaystyle е ^ <я \ омега т>>
Когда источник напряжения в этой цепи синусоидальный:
мы можем заменить v S ( т ) знак равно Re < V s ⋅ е я ω т > <\ displaystyle v_ (t) = \ operatorname
В сокращенной системе обозначений векторов дифференциальное уравнение сводится к
Решение для напряжения векторного конденсатора дает
В форме полярных координат это
Приложения
Цепные законы
С помощью векторов методы решения цепей постоянного тока могут применяться для решения линейных цепей переменного тока. Список основных законов приведен ниже.
Энергетика
Метод синхрофазоров использует цифровые инструменты для измерения векторов, представляющих напряжения системы передачи в широко распространенных точках сети передачи. Различия между векторами указывают на поток мощности и стабильность системы.
Телекоммуникации: аналоговые модуляции
Векторная диаграмма токов и напряжений
Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.
Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.
Определение
Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.
Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.
Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.
Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.
Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.
Разновидности
Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:
Векторную диаграмму токов можно построить 2 разными способами:
Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.
Построение
Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.
Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.
Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.
Способ 2
Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:
Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.
Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.
Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:
Далее нужно сделать:
Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.
Заключение
Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.
Видео по теме

Фазовый вектор
Читайте про фазовый вектор в фазовом пространстве системы: категории векторов и коэффициент частоты, косинусоидальная волна, роль амплитуды и периода колебаний.
Фазоры используют для анализа электрических систем в синусоидальном стационарном состоянии с равномерной угловой частотой.
Задача обучения
Основные пункты
Термины
Комплексные числа играют важную роль в физике. Чаще всего они записываются в терминах их действительной части, плюс мнимая. К примеру, а + bi, где a и b –действительные числа, i – мнимая часть.
Фазовый вектор (фазор) – представление синусоидальной функции, где амплитуда (А), частота (ω) и фаза (θ) выступают нестационарными по времени. Фазовые векторы делят на три категории, основываясь на этих показателях, потому что частотный коэффициент часто выступает общим для всех компонентов линейной комбинации синусоид. В таких ситуациях можно оставить только A и θ.
Пример последовательной схемы и соответствующей фазовой диаграммы для конкретной ω. Специалисты используют подобные диаграммы фазора для визуализации сложных постоянных и переменных. Стрелки отображают фазоры
Фазоры часто используют в электрике при рассмотрении напряжений, которые меняются синусоидально по времени.
Определение
Синусоиды можно отобразить математически в виде суммы двух комплексных функций:
Или как действительная часть одной из функций:
Фазовое представление сигналов
В нем заключается две идеи:
Когда τ положительно, то выступает «временной задержкой», описывающей время (больше нуля), когда достигается первый пик. Когда τ отрицательно – «временный прогресс», который описывает время (меньше нуля), когда достигнут последний пик. При подстановке = 2π/T, получим третий способ записи
В таком виде сигнал намного легче построить. Просто отобразите косинусоидальную волну с амплитудой и периодом. Потом уберите начало. В итоге, мы видим параметры со следующими единицами:
Синусоидально устойчивое состояние можно использовать для анализа поведения электрических и механических систем, достигших баланса – синусоидальное стабильное состояние.
В таком положении каждое напряжение и ток выступают синусоидальными с угловой частотой. Но их амплитуды и фазы отличаются. К примеру, напряжение на резисторе может привести к показателю напряжения на конденсаторе в 90° и задержать на индукторе на 90°. Можно рассмотреть подобную схему на рисунке. Стрелка с отметкой i(t) – ток, протекающий в ответ на приложенное напряжение.
Будем полагать, что источником напряжения выступает звуковой генератор:
Мы представляем это напряжение как комплексный сигнал:
Далее описываем источник напряжения на фазоре V и не забываем, что всегда можем определить фактическое напряжение, умножив на e iωt и получив действительную часть.
Обыкновенные дифференциальные уравнения Интерактивный учебник
Илья Щуров (НИУ ВШЭ)
4 Дифференциальные уравнения в многомерных фазовых пространствах
4.1 Многомерные фазовые пространства
4.1.1 Отступление: что такое фазовое пространство?
Пусть есть два города — A и B — и между ними проведены две дороги. Из города А в какой-то момент вышли Ромео и Джульетта и направились в сторону города B. При этом они решили идти каждый по своей дороге, держась за веревочку длиной 5 метров — Ромео за один конец, Джульетта за другой. Веревочка может не быть натянутой (то есть расстояние между Ромео и Джульеттой может быть меньше 5 метров, но не может быть больше), они могут притормаживать, ускоряться, пропускать друг друга вперед, идти назад и т.д. — двигаться как угодно. Известно, что двигаясь таким образом им удалось попасть из города A в город B.
В другой день из города B в город A выехал воз, нагруженный товаром, а из города A в город B выехал другой воз, тоже нагруженные товаром, и ехали они по разным тропинкам. Возы круглые (если смотреть сверху), их радиус 3 метра.
Пусть x — число лис, y — число кроликов. Если ни одной лисы нет, скорость роста числа кроликов пропорциональна числу самих кроликов (как в мальтузианской модели — какая-то часть популяции воспроизводится за единицу времени). Наоборот, если нет кроликов, то лисы вымирают от голода — за единицу времени какая-то доля популяции погибает. Каждая встреча лисы с кроликом (которые происходят с частотой, пропорциональной произведению x y ) вносит положительный вклад в динамику лис и отрицательный — в динамику кроликов. Запишем дифференциальное уравнение (систему из двух уравнений):
4.2 Дифференциальные уравнения в многомерных пространствах
Теперь мы готовы к тому, чтобы сформулировать общее определение дифференциального уравнения первого порядка с фазовым пространством произвольной размерности.
Понятия «система дифференциальных уравнений» и «дифференциальное уравнение с многомерным фазовым пространством» эквивалентны. Действительно, рассмотрим, например, систему из двух дифференциальных уравнений:
Здесь ситуация полностью аналогична линейной алгебре: нет никакой разницы между системой линейных уравнений и одним линейным уравнением относительно вектора (например, записанным в матричной форме).
4.2.1 Теорема существования и единственности решения задачи Коши
4.3 Автономные системы дифференциальных уравнений
4.3.1 Геометрия вектор-функций
Неверный ответ. Не совсем. Что насчёт ориентации?
Неверный ответ. Нет. Подставьте любое значение t и посмотрите, что получится.
Верный ответ. Верно!
Производная вектор-функции имеет следующую геометрическую интерпретацию: это вектор скорости точки, движущейся вдоль траектории. Естественно изображать векторы скорости на картинке с траекторией вектор-функции, откладывая их от соответствующих точек.
Формальное определение такое:
4.3.2 Автономные дифференциальные уравнения на плоскости
С интегральными кривыми связаны поля направлений; для фазовых кривых есть похожий объект: векторное поле.
Рассмотрим несколько примеров.
Неверный ответ. Это неверно: вся плоскость не может быть фазовой кривой, например, потому что не бывает дифференцируемого отображения из прямой на всю плоскость.
Неверный ответ. Не совсем верно. Есть ещё одна фазовая кривая.
Верный ответ. Так и есть!
Неверный ответ. Нет, в данном случае вертикальный луч является полноправной фазовой кривой: ничто не запрещает его рассматривать.
4.3.3 Особые и неособые точки векторного поля
4.4 Связь между автономными и неавтономными уравнениями
Сейчас мы обсудим одну из версий этого принципа.
С помощью теоремы 2 можно было бы получить уравнение на фазовые кривые, не находя явного вида решений. Для этого необходимо перейти к соответствующему неавтономному уравнению
4.4.1 Репараметризация фазовых кривых
Можно сказать, что при этом происходит репараметризация фазовых кривых: мы посещаем те же точки фазового пространства, но в другие моменты времени. Сформулируем необходимое определение.
Если представить себе, что на каждой точке кривой написано значение параметра, при котором мы проходим эту точку, то репараметризация — просто изменение «номеров» точек кривой.
Неформально можно сказать, что репараметризация кривой соответствует изменению скорости, с которой мы эту кривую обходим. Теперь легко понять, что при умножении векторного поля на константу мы изменяем скорость движения вдоль фазовых кривых, но не сами фазовые кривые. Более того: аналогичное утверждение справедливо при умножении векторного поля не только на константу, но и на любую положительную функцию.
Неверный ответ. Не вполне верно: на фазовой кривой есть стрелочка, показывающая направление движение. Что произойдёт с этими стрелочками?
Верный ответ. Верно! Именно так всё и будет.