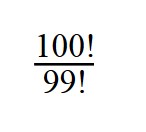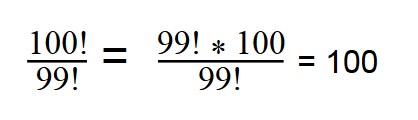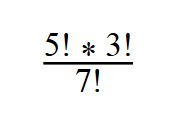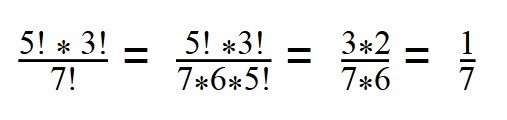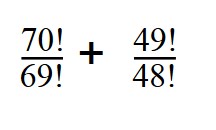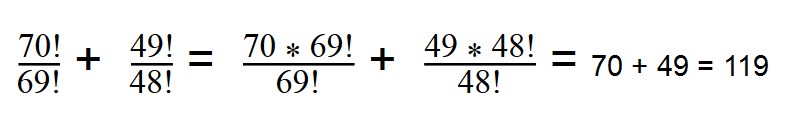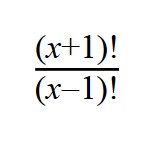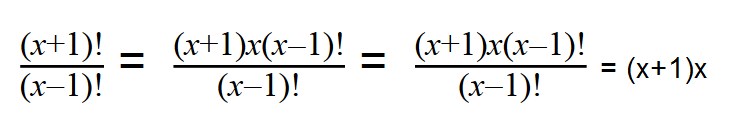что такое факториал в информатике
Программа для решения факториала на C++
Написать программу на C++ для вычисления(нахождения или решения) факториала — это очень популярное задание в сборниках по обучению программированию. Решение этой задачи и многих других размещено в разделе с решениями задач по программированию на C++. В данной статье мы разберем как реализовать решение на языке программирования C++.
Для начала — что такое факториал?
Факториал — это произведение всех натуральных чисел от 1 до N включительно. То есть, если N = 5, то значение факториала
Решить данную задачу можно несколькими способами, мы рассмотрим рекурсивное вычисление факториала и циклическое.
Программа для решения факториала на C++ : 5 комментариев
Очень полезная статья, сразу все стало понятно))Спасибо!
int n_factorial(int n);
int main()
<
int n, res;
printf(» [ n factorial finder ] \n\n»);
for(int sucl=0; sucl==0;) <
printf(» n = «);
scanf(«%i»,&n);
if(n==0) <
printf(» %i! = 1″,n);
> else
if(n>0) <
res=n_factorial(n);
printf(» %i! = %i»,n,res);
> else
if(n
Найти сумму 10 членов ряда, в котором an=(n!)/n2.
В качестве проекта необходимо написать программу для нахождения разности факториалов наименьшего и наибольшего чисел из N введенных с использованием структур языка JavaScript.
Вводится N(в данном случае 5) чисел: 1,2,3,4,5;
Находится наибольшее и наименьшее из них: 5 и 1 соответственно;
Вычисляется разность факториалов наименьшего и наибольшего чисел из N введенных: 1!-5!=-119
Требования к выполнению проекта: наличие написанной функции, циклов и условий.
Пожалуйста помогите решить задачу
В качестве проекта необходимо написать программу для нахождения разности факториалов наименьшего и наибольшего чисел из N введенных с использованием структур языка JavaScript.
Вводится N(в данном случае 5) чисел: 1,2,3,4,5;
Находится наибольшее и наименьшее из них: 5 и 1 соответственно;
Вычисляется разность факториалов наименьшего и наибольшего чисел из N введенных: 1!-5!=-119
Требования к выполнению проекта: наличие написанной функции, циклов и условий.
Помогите пожалуйста!!
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Факториал программа на паскале
Факториал – произведение натуральных чисел от единицы до заданного числа. Имеет условное обозначение в виде восклицательного знака. n!=1*2*3*. *n (Например: 3!=1*2*3=6).
В Turbo Pascal факториал находится, как правило, двумя способами: с помощью цикла или с помощью рекурсии.
Вычисление факториала в pascal с помощью цикла
Данный способ нахождения факториала исключительно прост. В цикле от 1 до n умножается число само на себя. При этом необходимо учитывать условие, что 0!=1. Ниже представлена реализация программы с помощью цикла for. Аналогично используются repeat и while.
if (n=0) then writeln(‘0!=1’) else
Факториал числа – Вычисление с помощью цикла (1 способ)
Факториал – Нахождение факториала в паскале с помощью рекурсии (2 способ)
Задача
Факториал числа представляет собой произведение всех натуральных чисел от 1 до этого числа включительно. Например, факториал числа 7 выглядит так:
1 * 2 * 3 * 4 * 5 * 6 * 7
Факториал числа обозначается как само число после которого следует восклицательный знак. Например, 7!. Таким образом:
7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040
С увеличением числа его факториал быстро возрастает. Так если 3! = 6, то уже 10! = 3628800. Поэтому для натуральных чисел больше 12-ти в языке программирования Паскаль просто так факториал вычислить нельзя.
Допустим, требуется определить факториал числа, которое ввел пользователь.
Решение
Переменной factorial сначала присваивается значение 1.
0! = 1 и 1! = 1.
Если пользователь ввел число больше единицы, то выполняется цикл, в теле которого на каждой итерации значение переменной factorial умножается на следующее натуральное число (переменную i ).
Обучение программированию идёт по пути от простого к сложному. Освоив типы данных и операторы языка, переходят к циклическим конструкциям. Задач на циклы существует бесчисленное количество: начиная от вывода цифр в столбик до подсчёта сумм по сложным формулам. Тем не менее у начинающих программистов остаётся вопрос: «Как вычислить факториал в «Паскале»?»
Реализовать задачу можно как минимум тремя способами. Отличаются они используемыми операторами.
Математические сведения
Перед тем как перейти к построению алгоритмов и написанию программ, следует изучить теорию. В математике факториалом называют произведение целого числа, для которого вычисляется выражение, на целые положительные числа меньше его.
Понять определение поможет пример. Пусть требуется выполнить нахождение факториала для числа 3. Решение: 3! = 3 * 2 * 1 = 6.
Обозначается действие восклицательным знаком, который ставится после числа. Важное замечание: факториал определён только для целых положительных чисел. Вместе с тем, введено понятия для нуля: 0! = 1.
Считать выражение для больших значений вручную – занятие долгое. Чтобы убыстрить процесс вычислений, используют компьютерные программы. Далее рассмотрены способы, как найти факториал в «Паскале».
Первый способ
Код ниже показывает вариант программы.
В примере используют составную конструкцию с условием, которое записывается перед телом цикла. Синтаксис записи:
Выполняется код следующим образом: программа проверяет истинность выражения , в случае положительной проверки переходит на .
Возвращаясь к программе, нужно обратить внимание на следующие строки:
Второй способ
Следующий предлагает вычислить факториал в «Паскале» с помощью оператора repeat.
Конструкция цикла: repeat until ;
Чтобы понять, как работает программа, рассмотрим её построчно:
Третий способ
Последняя программа также дает возможность вычислить факториал в «Паскале» и является самой компактной по размеру. Причина – используемый оператор for, для которого увеличение счётчика i задаётся в параметрах цикла.
Работает код следующим образом (цифрами указаны строки листинга):
Замечание
Даже для чисел из первой десятки факториал имеет значение больше, чем допускает тип данных integer. Поэтому программа в «Паскале» покажет сообщение об ошибке. Исправить её просто – нужно заменить тип данных для переменной-результата на longint или использовать типы для хранения вещественных значений.
Алгоритмы быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
Реализуем описанный алгоритм:
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
График с линейной шкалой
График с логарифмической шкалой
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
Исходные коды реализованных алгоритмов приведены под спойлерами
Факториал
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
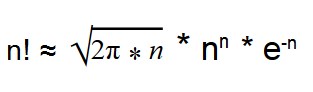 |
Рекуррентная формула
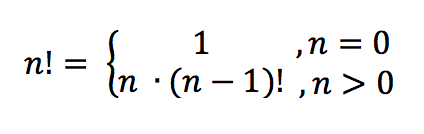 |
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
0! = 1? или почему факториал нуля равен единице
Давным давно, еще в классе 10-ом (лет 8 назад) я случайно обнаружил довольно нехитрое объяснение того, почему факториал нуля равен единице.
Я рассказывал про это многим учителям, но никого не торкнуло. Поэтому я просто выложу это знание здесь, а то вдруг кому-то пригодится или наведет на определенные мысли. Сразу скажу я не математик, наткнулся на это случайно, когда игрался с числами. Я тогда даже не знал что такое факториал 🙂
Для начала вспомним общую теорию:
Факториа́л числа n — произведение всех натуральных чисел до n включительно:
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
На самом же деле факториал нуля вполне вычислим!
Для этого нам нужно проделать простую последовательность обычных математических операций.
Попробуем в действии на примере факториала n = 4 (4! = 1 * 2 * 3 * 4 = 24)
На выходе получаем ряд чисел количество которых меньше на 1:
50 110 194
(110 — 50) (194 — 110)
В результате мы получаем факториал числа четыре.
Попробуем вычислить этим способом факториал 3 (3! = 1 * 2 * 3 = 6)
Берем четыре числа в степени 3 и вычисляем «пирамидальную разность» (сам придумал)
1 3 2 3 3 3 4 3
1 8 27 64
(8 — 1) (27 — 8) (64 — 27)
7 19 37
(19 — 7) (37 — 19)
Ну и для 1 попробуем (1! = 1)
Все очень просто и для нуля:
Берем n + 1 чисел в степени 0, тоесть достаточно и одного
Вуaля! Любое число в степени 0 равно 1. В этом, кстати, слабость моего способа, он использует определение.
Но тем не менее, я считаю, что это здорово 🙂