Что такое энтропия источника сообщений
Информационная энтропия
Так, возьмём, например, последовательность символов, составляющих какое-либо предложение на русском языке. Каждый символ появляется с разной частотой, следовательно, неопределённость появления для некоторых символов больше, чем для других. Если же учесть, что некоторые сочетания символов встречаются очень редко, то неопределённость ещё более уменьшается (в этом случае говорят об энтропии n-ого порядка, см. Условная энтропия).
Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу. Ср. тж. Термодинамическая энтропия
Содержание
Формальные определения
Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле:
Эта величина также называется средней энтропией сообщения. Величина называется частной энтропией, характеризующей только i-e состояние.
Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.
Шеннон вывел это определение энтропии из следующих предположений:
Шеннон показал, что любое определение энтропии, удовлетворяющее этим предположениям, должно быть в форме:
где K — константа (и в действительности нужна только для выбора единиц измерения).
В общем случае b-арная энтропия (где b равно 2,3. ) источника = (S,P) с исходным алфавитом S = <a1, …, an> и дискретным распределением вероятности P = <p1, …, pn> где pi является вероятностью ai (pi = p(ai)) определяется формулой:
Условная энтропия
Если следование символов алфавита не независимо (например, во французском языке после буквы «q» почти всегда следует «u», а после слова «передовик» в советских газетах обычно следовало слово «производства» или «труда»), количество информации, которую несёт последовательность таких символов (а следовательно и энтропия) очевидно меньше. Для учёта таких фактов используется условная энтропия.
Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (т.е. вероятности двухбуквенных сочетаний):
где — это состояние, зависящее от предшествующего символа, и — это вероятность , при условии, что был предыдущим символом.
Так, для русского алфавита без буквы « ё » [1]
Через частную и общую условные энтропии полностью описываются информационные потери при передаче данных в канале с помехами. Для этого применяются т.н. канальные матрицы. Так, для описания потерь со стороны источника (т.е. известен посланный сигнал), рассматривают условную вероятность получения приёмником символа при условии, что был отправлен символ . При этом канальная матрица имеет следующий вид:
| | | . | | . | | |
|---|---|---|---|---|---|---|
| | | | . | | . | |
| | | | . | | . | |
| . | . | . | . | . | . | . |
| | | | . | | . | |
| . | . | . | . | . | . | . |
| | | | . | | . | |
Очевидно, вероятности, расположенные по диагонали описывают вероятность правильного приёма, а сумма всех элементов столбца даст вероятность появления соответствующего символа на стороне приёмника — . Потери, приходящиеся на предаваемый сигнал , описываются через частную условную энтропию:
Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:
означает энтропию со стороны источника, аналогично рассматривается — энтропия со стороны приёмника: вместо всюду указывается (суммируя элементы строки можно получить , а элементы диагонали означают вероятность того, что был отправлен именно тот символ, который получен, т.е. вероятность правильной передачи).
Взаимная энтропия
Взаимная энтропия, или энтропия объединения, предназначена для рассчёта энтропии взаимосвязанных систем (энтропии совместного появления статистически зависимых сообщений) и обозначается , где , как всегда, характеризует передатчик, а — приёмник.
Взаимосязь переданных и полученных сигналов описывается вероятностями совместных событий , и для полного описания характеристик канала требуется только одна матрица:
| | | … | | … | |
| | | … | | … | |
| … | … | … | … | … | … |
| | | … | | … | |
| … | … | … | … | … | … |
| | | … | | … | |
Для более общего случая, когда описывается не канал, а просто взаимодействующие системы, матрица необязательно должна быть квадратной. Очевидно, сумма всех элементов столбца с номером даст , сумма строки с номером есть , а сумма всех элементов матрицы равна 1. Совместная вероятность событий и вычисляется как произведение исходной и условной вероятности,
Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:
Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:
Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределённость на пару символов — отправленного и полученного. Путём несложных преобразований также получаем
Взаимная энтропия обладает свойством информационной полноты — из неё можно получить все рассматриваемые величины.
Свойства
Альтернативное определение
Другим способом определения функции энтропии H является доказательство, что H однозначно определена (как указано ранее), если и только если H удовлетворяет пунктам 1)—3):
1) H(p1, …, pn) определена и непрерывна для всех p1, …, pn, где pi [0,1] для всех i = 1, …, n и p1 + … + pn = 1. (Заметьте, что эта функция зависит только от распределения вероятностей, а не от алфавита.)
2) Для целых положительных n, должно выполняться следующее неравенство:
3) Для целых положительных bi, где b1 + … + bn = n, должно выполняться равенство:
Эффективность
Исходный алфавит, встречающийся на практике, имеет вероятностное распределение, которое далеко от оптимального. Если исходный алфавит имел n символов, тогда он может может быть сравнён с «оптимизированным алфавитом», вероятностное распределение которого однородно. Соотношение энтропии исходного и оптимизированного алфавита — это эффективность исходного алфавита, которая может быть выражена в процентах.
Из этого следует, что эффективность исходного алфавита с n символами может быть определена просто как равная его n-арной энтропии.
История
Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication», опубликованной в двух частях в Bell System Technical Journal в 1948 году.
Литература
См. также
Внешние ссылки
Эта статья содержит материал из статьи Информационная энтропия русской Википедии.
Энтропия? Это просто!
Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What’s an intuitive way to understand entropy?, заданный на сайте Quora
Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание. 
Так что же такое энтропия?
Энтропия — это то, как много информации вам не известно о системе
Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.
Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём). 
Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).
А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.
Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.
Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:
Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B. 
Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.
Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.
Физический пример: газ под поршнем
Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях.
Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:
Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.
Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.
Твёрдые тела и потенциальная энергия
Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия.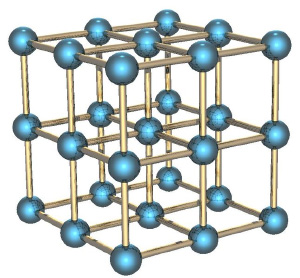 
Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.
Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.
Понимаем второй закон термодинамики
Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад. 
Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.
Перемешивание газов
И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.
Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).
Разбираемся с демоном Максвелла
Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа.
Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?
Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.
Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.