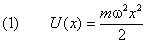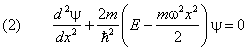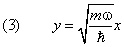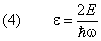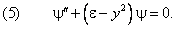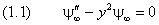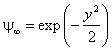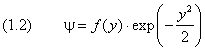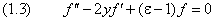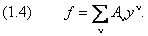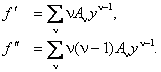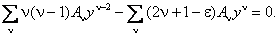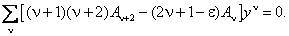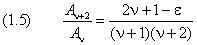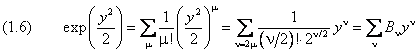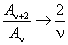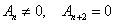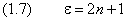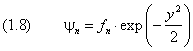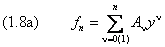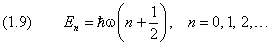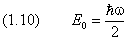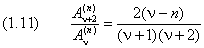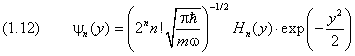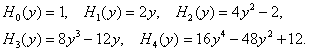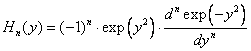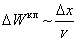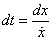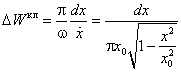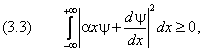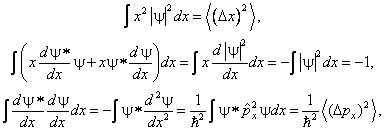Что такое энергия нулевых колебаний гармонического осциллятора

Что такое энергия нулевых колебаний гармонического осциллятора

Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы .

Потенциальная энергия частицы

где .

Гармонический осциллятор в квантовой механике описывается уравнением Шредингера:

Значения Ψ-функции мы находить не будем. Нас интересуют значения полной энергии осциллятора:

не зависит от n, в отличие от прямоугольной потенциальной ямы, рассмотренной нами в п. 5.2.

Минимальная энергия называется нулевой энергией, т.е. при колебания атомов К в кристаллической решетке не прекращаются.

В квантовой механике вычисляется вероятность различных переходов квантовой системы из одного состояния в другое. Для гармонического осциллятора возможны лишь переходы между соседними уровнями.

Условия, накладываемые на изменения квантовых чисел при переходах системы из одного состояния в другое, называются правилами отбора. Для гармонического осциллятора правило выражено формулой:

.

Из (5.3.4) вытекает, что энергия квантового осциллятора изменяется только порциями, т.е. квантуется. Причем, как и в прямоугольной яме, энергия ограничена снизу минимальным значением

– энергия нулевых колебаний (прямое следствие соотношения неопределенностей). Это означает, что частица не может находиться на дне потенциальной ямы.

Плотность вероятности нахождения частицы изображена на рис. 5.2. Как и в случае прямоугольной потенциальной ямы, при n = 2 в середине ямы частица находиться не может. Это совершенно непонятно с классической точки зрения. Квантуется не только энергия, но и координата частицы.

Источник

Что такое энергия нулевых колебаний гармонического осциллятора

Линейным гармоническим осциллятором называется система, потенциал ьная энерги я которой квадратично зависит от координаты:

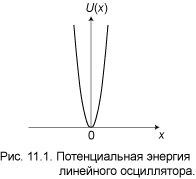
Здесь m — масса частицы, а ω — собственная частота осциллятора. На рис. 11.1 зависимость (1)

изображена графически. Кривая U ( x ) своей крутизной и бесконечно большой высотой напоминает потенциал ьную яму. Ниже мы увидим, что линейный осциллятор, действительно, проявляет некоторые свойства частицы в бесконечно высокой потенциал ьной яме. Например, он имеет бесконечное число дискретных уровней. Но в отличие от отвесных стенок ямы, потенциал осциллятора растёт плавно, и, как следствие, появляется некоторая вероятность обнаружить частицу достаточно далеко от начала координат. Плавная форма потенциал а позволяет осциллятору при определённых условиях проявить свойства классической (не квантовой) частицы. Для этого достаточно, чтобы длина волны де Бройля была меньше характерных размеров области изменения потенциал а. В случае потенциал ьной ямы, либо потенциал ьного барьера, такая возможность полностью исключена, так как там потенциал меняется скачком в одной точке. Перейдём к количественному решению задачи.

Напишем одномерное уравнение Шредингера с потенциал ьной энерги ей (1):

У него нет естественных граничных условий. Дискретные уровни энерги и получаются как следствие ограниченности волновой функции.

Преобразуем уравнение (2): вместо координаты x введём безразмерный аргумент

и вместо E — безразмерную энерги ю осциллятора

Квантовые свойства осциллятора имеют многочисленные приложения в атомной физике. Ниже мы рассмотрим два из них: влияние нулевых колебаний электромагнитного вакуума на функцию Планка и связанный с ними лэмбовский сдвиг метастабильного уровня атома водорода.

11.1 Решение волнового уравнения

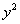
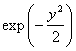
Множитель перед функцией появляется при двукратном дифференцировании экспоненты , а именно:

В области больших значений аргумента можно пренебречь единицей по сравнению с y 2 в множителе 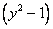. Следовательно, рассматриваемая экспонента может служить асимптотическим приближением точного решения:

Решение уравнения (5) при произвольных значениях аргумента будем искать в виде

Согласно (5), функция f ( y ) удовлетворяет уравнению

Ищем решение в виде ряда:

Дважды продифференцируем искомую функцию

Подставив эти разложения в (1.3), получим бесконечную цепь линейных уравнений для коэффициентов разложения A _ν :

Соберем степени с одинаковыми показателями, для чего индекс первой суммы увеличиваем на два:

Здесь ν принимает только чётные значения. Мы ввели обозначение

Теперь ясно, что функция, описываемая соотношением (1.5), растёт быстрее, чем экспонента (1.6). Следовательно, произведение (1.4) при больших значениях аргумента неограниченно возрастает. Поэтому физический смысл имеет только такое решение (1.3), в котором сумма (1.4) содержит лишь конечное число слагаемых.

Покажем, как требование конечности числа слагаемых приводит к дискретному спектру энергетических уровней осциллятора. Пусть n — номер последнего члена ряда (1.4), не равного нулю:

Из (1.5) вытекает связь между величиной энергетического уровня и его номером:

Итак, мы снова получили дискретные уровни энерги и. Каждому уровню с номером n соответствует ровно одна волновая функция:

причём нижний предел равен нулю при чётном n и единице — при нечётном. Уровни энерги и, согласно (4) и (1.7), принимают дискретный ряд значений:

Обратим внимание на то, что наименьшее из возможных значений энерги и, равное

Рекуррентное соотношение (1.5) с учётом (1.7) принимает вид

Приведём несколько первых полиномов Эрмита:

Исследуем полученное решение.

11.2 Свойства квантового осциллятора

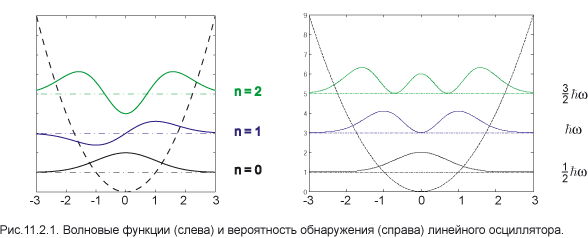
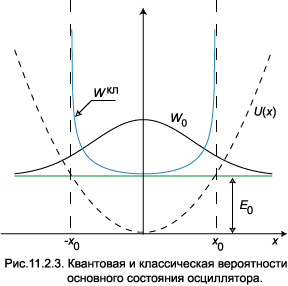
Парабола изображает потенциал ьную функцию, а горизонтальные прямые — значения энергетических уровней. Для удобства восприятия волновые функции сдвинуты по вертикальной оси.

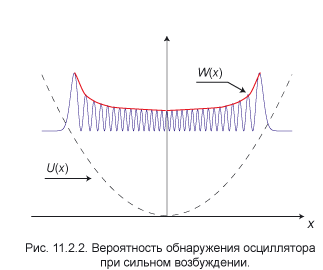
В состояниях с сильным возбуждением квантовый осциллятор приобретает свойства классической частицы. На рис. 11.2.2 схематически изображён график вероятности в

В точках поворота скорость обращается в нуль, поэтому там легче всего найти частицу. В самом деле, рассмотрим движение частицы по закону

Классическую вероятность обнаружения частицы на отрезке от x до x + dx определим как отношение времени прохождения отрезка

к половине периода колебаний:

обозначает уровень нулевых колебаний E ₀ из (1.10). Классическая вероятность увеличивается по мере приближения к точке x ₀, определяемой условием U ( x ₀) = E ₀, но не может перейти через эту границу. Квантовая теор ия предсказывает уменьшение вероятности при приближении к границе, причём частица может быть обнаружена в классически недоступной области x > x ₀.

11.3. Нулевые колебания

В самом низком состоянии осциллятор имеет отличную от нуля энерги ю (1.10), определяемую его собственной частотой. Нулевые колебания осциллятора имеют чисто квантовую природу и находят своё объяснение в соотношении неопределённостей. Полная энерги я осциллятора равна сумме кинетической и потенциал ьной

.

.

.

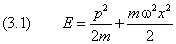
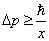
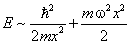
Полная энерги я как функция x имеет минимум в точке

,

.

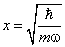
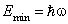
Полученное значение в два раза отличается от результата точного расчёта. Это не удивительно, так как соотношение неопределёностей даёт оценки лишь по порядку величины. Точное выражение для энерги и нулевых колебаний получается из упомянутого в главе неравенства для дисперсий момента и координаты:

,
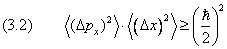
Формально она выводится следующим образом. Пусть состояние частицы описывается функцией y ( x ), причём средние значения импульса и координаты для простоты вывода предполагаются равными нулю. Напишем очевидное неравенство

где a — действительная постоянная. Далее вычислим три полезных выражения:

Они позволяют преобразовать левую часть (3.3) в квадратичный по a трёхчлен:

Источник

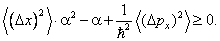
Квантовый гармонический осциллятор

Конспект лекции (с демонстрациями)

Аннотация: изучение качественной стороны решения уравнения Шредингера для гармонического осциллятора, выяснение отличий получаемых результатов от выводов классической механики. (Традиционное изложение темы, дополненное демонстрациями на компьютерных моделях.)

Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой

В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.

Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:

Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы «зависает», и там вероятность обнаружения максимальна.

Оценка минимальной энергии осциллятора

Посмотрим, к каким выводам о характере движения приводит квантовая механика. Начнем с простой оценки минимального значения энергии осциллятора E. Полная энергия осциллятора E складывается из кинетической и потенциальной энергий:

Используя соотношение неопределенности Гейзенберга, в качестве оценки значения импульса p возьмем p

Для малых значений x кинетическая энергия превышает потенциальную, тогда как при больших значениях x имеет место обратное соотношение между ними. Для основного состояния, где энергия минимальна, найдем минимум функции (2). Значение переменной x_min, соответствующее минимуму, равно:

а соответствующее значение энергии E имеет порядок

Заметим, что оценка энергии основного состояния дает ненулевое(!) значение. Уже простые вычисления приводят к нетривиальному результату.

Решения уравнения Шредингера

Нахождение точного решения требует решения уравнения Шредингера с потенциальной энергией (1), которое имеет вид

Первые три волновых функции гармонического осциллятора выглядят так:

Здесь введено обозначение x₀ 2 = h/(4π 2 mυ).

Графики этих волновых функций представлены на рисунке ниже.

Пунктиром показаны границы, между которыми совершала бы колебания классическая частица. Значения a₀ отличаются для разных n, так как от n зависит энергия Е (

Компьютерная модель поможет Вам в исследовании квантового осциллятора. Ее возможности: после того, как Вы зададите порядковый номер атомов Z, из которых состоит молекула (по умолчанию Z=8), компьютер проведет необходимые расчеты и будет готов показать разрешенные значения энергии, соответствующие им волновые функции и распределения плотности вероятности нахождения частицы по координате. Двигайте указатель вдоль оси энергий (мышкой или клавишами со стрелками) и наблюдайте.

Смешение состояний (принцип суперпозиции)

Коэффициенты этого разложения

Вероятность осциллятору находиться в состоянии с квантовым числом n равна

т.е. дается распределением Пуассона. Волновая функция Ψ(x,t) представляет нерасплывающийся волновой пакет. Центр пакета движется по классическому закону, ширина пакета не зависит от времени.

Эти состояния называют когерентными, так как они используются для описания когерентных свойств электромагнитного излучения в квантовой теории поля (R. Glauber, Нобелевская премия 2005 года; текст нобелевской лекции, 269 кб). Можно показать, что свободное электромагнитное поле эквивалентно бесконечному набору независимых гармонических осцилляторов.

Со свойствами когерентных состояния гармонического осциллятора можно познакомиться поближе с помощью компьютерной модели (автор L. Kocbach).

Вычисление средних значений

Аналогичным образом находится среднее значение любой функции координаты, например, для потенциальной энергии имеем

В этих формулах, чтобы вычислить среднее значение, мы умножаем значение функции в точке x на вероятность нахождения частицы около x и суммируем по всем возможным значениям x. В качестве примера найдем эти величины для основного состояния гармонического осциллятора

т.к. под интегралом нечетная функция, и

Среднее значение потенциальной энергии равно половине полной энергии этого состояния.

Правило для вычисления средней кинетической энергии отличается от приведенного, т.к. кинетическая энергия является функцией импульса p, а не координаты x:

Для основного состояния гармонического осциллятора

Энергия излучения при переходе из одного состояния в другое равна

где n и m квантовые числа начального и конечного состояний, среднее значение координаты не меняется во времени, и такие переходы запрещены.

Проверим выполнение этого условия для гармонического осциллятора. Пусть n=1, а m=0. Опуская постоянные, для интеграла получим выражение

т.к. под интегралом четная функция. Если положить n=2, m=1,

по той же причине. Переходы между соседними уровнями 0↔1 и 1↔2 являются разрешенными. Рассмотрим теперь переход между состояниями n=0 и m=2. Соответствующий интеграл имеет вид

поскольку функция под интегралом нечетная, а пределы симметричны относительно x=0. Следовательно, переходы 0↔2 запрещены. Особенности испускания и поглощения электромагнитного излучения гармоническим осциллятором таковы, что возможны переходы только между соседними уровнями Δn = ± 1. Это правило отбора для гармонического осциллятора.

Трехмерный гармонический осциллятор

В общем случае потенциальная энергия выражается суммой

Уравнение Шредингера допускает разделение переменных. Если решение искать в виде ψ(x,y,z)=X(x)Y(y)Z(z), получается три дифференциальных уравнения, совпадающих по виду с одномерным. Для изотропного случая (k_x =k_y =k_z = k) значения энергии таковы

где квантовые числа n₁, n₂ и n₃ пробегают значения от 0 до бесконечности. Как и в одномерной задаче, налицо дискретность значений энергии, не равная нулю нулевая энергия. Но в трехмерном случае решение определяется тремя квантовыми числами. И особенность: одно и то же значение энергии могут иметь различные состояния, для которых выполнено условие n₁+n₂+n₃ = const. Такие состояния называют вырожденными.

Взаимодействие двух осцилляторов

Существование нулевой энергии (формула (3) при n = 0) сыграло важную роль для объяснения такого загадочного явления, как межатомное взаимодействие у благородных газов. Так как это взаимодействие проявляется в уравнении состояния Ван-дер-Ваальса для реальных газов

оно названо ван-дер-ваальсовским. Если молекулы (атомы) обладают дипольным моментом, то их притяжение обусловлено взаимодействием диполей (качественно и количественно исследованный факт). Но нейтральные молекулы с симметричным в состоянии покоя распределением заряда могут взаимодействовать только при смещении зарядов, вызывающем появление дипольного момента. Такое смещение возникает при не исчезающих ни при каких условиях нулевых колебаний с энергией hυ/2. Появление дипольного момента у одной молекулы индуцирует дипольный момент в другой. Взаимодействие этих быстро меняющихся моментов и обуславливает притяжение.

В отсутствии второго (или при очень большом R) потенциальная энергия каждого осциллятора может быть рассчитана по формуле (1), а частоту колебаний обозначим через υ₀

Энергия взаимодействия двух диполей по закону Кулона равна

выражение для полной энергии приводится к виду

представляющему сумму энергий двух независимых осцилляторов с несколько отличающимися частотами

Как мы видели, энергия этих осцилляторов имеет квантованные значения (см. (3) выше) и, следовательно, полная энергия нашей системы будет

а для основного состояния (n₁ = 0 и n₂ = 0)

Теперь надо учесть, что вторые слагаемые под корнями много меньше первых (связь электрона со своим ядром гораздо сильнее связи осцилляторов). Корни квадратные разложим в степенные ряды и ограничимся тремя членами в разложении. Это даст

Последнее выражение равно удвоенной энергии изолированного осциллятора минус небольшая энергия. Поскольку добавка отрицательна, полная энергия взаимодействующих осцилляторов меньше энергии изолированных, для разрыва связи нужно энергию затратить! И, заметим, энергия связи очень быстро убывает с расстоянием

Не было бы нулевых колебаний (чисто квантового эффекта), не существовало бы и связи молекул в основном состоянии.

Ангармонический осциллятор

Если возникли какие-либо вопросы, напишите мне.

Источник