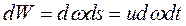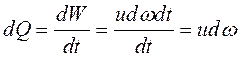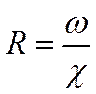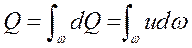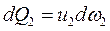Что такое элементарная струйка

Элементарная струйка

Через любую точку Апотока (рис.3.3) всегда можно провести линию, в каждой точке которой вектор местной скорости в данный момент времени направлен по касательной к ней.

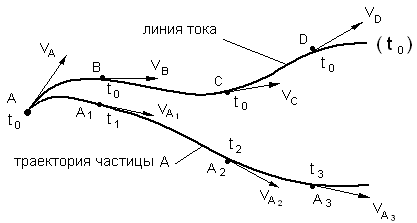
Линией тока называется линия, в каждой точке которой вектор скорости в данный момент времени направлен по касательной. Это понятие является центральным в методе Эйлера.

Рис. 3.3. Линия тока и траектория частицы жидкости

Траекториейназывается путь, который описывает точка при своём движении. При установившемся движении линия тока и траектория частицы совпадают. В общем случае неустановившегося движения в следующий момент времени через ту же точку А может проходить уже другая линия тока.

Вектор скорости с компонентами касателен к линии тока, т.е. совпадает по направлению с элементами линии тока , имеющего проекции на оси координат. Воспользуемся известным условием параллельности двух векторов – их проекции на оси координат должны быть пропорциональны друг другу

.

Полученное условие является уравнением линии тока в дифференциальной форме.

В частном случае при установившемся движении каждая линия тока сохраняет своё положение в пространстве и одновременно становится линией, по которой перемещаются частицы, т.е. совпадает с траекторией.

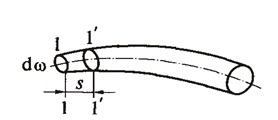
Элементарной струйкой называется совокупность линий тока, проходящих через все точки бесконечно малой площадки (рис.3.4).

Рис.3.4. Элементарная струйка и трубка тока

При установившемся движении элементарная струйка сохраняет с течением времени постоянными свою форму, размеры и положение в пространстве, что является следствием аналогичного свойства составляющих её линий тока.

При стремлении поперечных размеров струйки к нулю она в пределе стягивается в линию тока.

Боковая поверхность элементарной струйкиназываетсятрубкой тока(рис.3.4). Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.

В случае установившегося движения элементарная струйка обладает следующими тремя свойствами:

1) Форма элементарной стройки не меняется во времени, т.к. при установившемся движении не меняется форма линий тока;

2) Поверхность элементарной струйки (трубки тока) непроницаема, т.е. перетекание через боковые стенки отсутствует. Частицы жидкости, движущиеся в одной линии тока, не могут принадлежать другим;

3) Скорость и давление для всех точек данного поперечного сечения струйки постоянны, однако вдоль струйки эти величины могут меняться.

Таким образом, при установившемся движении элементарная струйка сохраняет с течением времени постоянными свою форму, размеры и положение в пространстве. Массообмен через боковую поверхность исключён, и движение жидкости возможно только вдоль элементарной струйки.

Если учесть несжимаемость жидкости, то получим следствие, лежащее в основе одного из центральных положений гидравлики, – уравнение неразрывности: объём жидкости, прошедший через любое поперечное сечение с площадью за время , должен равняться объёму жидкости, прошедшему через любое другое сечение с площадью за то же время.

Невыполнение сформулированного условия привело бы к изменению массы жидкости между двумя сечениями, что противоречит свойствам принятой модели жидкости как несжимаемой среды.

Источник

Элементарная струйка

Если в движущейся жидкости выделить в плоскости, перпендикулярной течению, элементарную бесконечно малую площадку 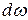(рис. 3.3) и через все точки, находящиеся на ее контуре, провести линии тока для данного момента времени, то получившаяся поверхность называется трубкой тока, а находящаяся в ней жидкость образует элементарную струйку, которая обладает следующими свойствами:

— форма элементарной струйки при установившемся движении остается неизменной во времени, так как в этом случае линии тока с течением времени не меняют своей формы;

— вхождения в элементарную струйку внешних линий тока и выхода из нее содержащихся в ней линий тока не происходит, так как боковая поверхность элементарной струйки образована линиями тока, к которым скорости направлены по касательной;

— скорости во всех точках поперечного сечения элементарной струйки можно считать одинаковыми вследствие незначительности поперечного сечения элементарной струйки.

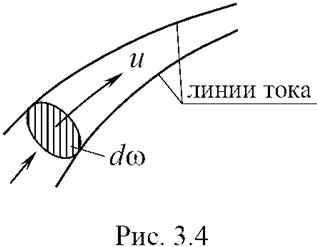
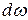
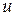
Рассмотрим элементарную струйку потока с поперечным сечением (см. рис. 3.3) и постоянной скоростью движения частиц по сечению струйки.

Рисунок 3.3 Элементарная струйка

,

— путь, пройденный за единицу времени, т.е. скорость движения жидкости .

, (3.4)

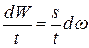
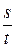
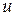
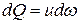
т. е. расход струйки равен произведению площади ее поперечного сечения на скорость в этом сечении.

Источник

Элементарная струйка и поток.

Трубкой тока называется трубчатая поверхность бесконечно малого поперечного сечения, образованная системой линий тока, проходящих через точки бесконечно малого замкнутого контура (рис. 3.4).

Жидкость, протекающая внутри этой трубки, называется элементарной струйкой. Элементарная струйка изолирована от окружающей массы жидкости. Очевидно, жидкость не может протекать через боковую поверхность трубки тока, так как на ней u_n = 0. Совокупность элементарных струек представляет собой поток конечных размеров. Струйная модель потока

жидкости упрощает теоретические исследования движения жидкости. Основные свойства элементарной струйки:

1. Скорость и площади сечений элементарной струйки могут меняться вдоль струйки, скорости же в пределах одного сечения элементарной струйки вследствие малости площадки одинаковы.

2. Жидкость не может протекать через боковую поверхность элементарной струйки, так как на основании определения линии тока в любой точке поверхности элементарной струйки скорость направлена по касательной к поверхности.

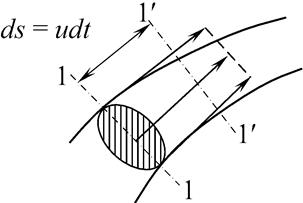
Объем жидкости, проходящей в единицу времени через данное поперечное сечение струйки, называется элементарным расходом. За время dt (рис. 3.5) все частицы из сечения 1-1 переместятся на расстояние ds = udt в сечении 1’–1’. Здесь u – скорость движения частиц. Объем жидкости между сечениями

За единицу времени проходит количество жидкости в объеме, равном:

Единица измерения м3/с. Массовый расход dG = dQρ = ρudω, кг/с. Весовой расход dGg = dGg = ρgudω, Н/с.

Гидравлические элементы потока.

Живым сечением потока ω называется поперечное сечение потока, нормальное к направлению движения и ограниченное его внешним контуром.

Смоченным периметром χ называется длина контура живого сечения, на которой жидкость соприкасается с твердыми стенками.

Гидравлическим радиусом называется отношение площади живого сечения потока ω к смоченному периметру χ:

Для круглого сечения R = π r2 / (2 π r) = r / 2 = d / 4.

Средняя скорость потока и расход.

Средняя скорость потока и расход.

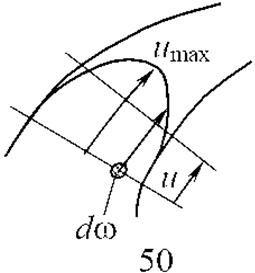
Поток представляет собой совокупность элементарных струек (рис. 3.6).

Из рис. видно, что скорость в отдельных струйках различна.

Расход потока Q равен сумме расходов элементарных струек, т.е.

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Уравнение неразрывности.

Для двух сечений 1–1 и 2–2 элементарной струйки в установившемся движении (рис.3.7) можно записать: и

Источник

Вопрос №23. Что такое траектория, линия тока, труба тока, элементарная струйка, живое сечение, смоченный периметр, гидравлический радиус?

Траектория— след движущейся частицы.

Линия тока— линия, в каждой точке которой вектор скорости направлен по касательной. При установившемся движении линия тока совпадает с траекторией движущейся частицы.

Трубка тока— элементарная площадка, через контур которой проведены линии тока.

Элементарная струйка— часть жидкости ограниченная трубкой тока.

Совокупность линий тока проходящих через элементарную площадку.

Элементарная струйка обладает следующими свойствами:

1. форма элементарной струйки остается неизменной во времени.

2. обмен частицами между отдельными струйками не возможен (вектор скорости направлен по касательной, нормальная составляющая равна 0).

3. скорость и давление во всех точках сечения одинаковы в виду малости сечения.

Элементы потока

Смоченный периметр— часть периметра, на котором поток соприкасается с твердыми стенками.

`Гидравлический радиус – отношение площади живого сечения к смоченному периметру

`Для круглого сечения R = π r2 / (2 π r) = r / 2 = d / 4.

Дата добавления: 2015-04-18 ; просмотров: 24 ; Нарушение авторских прав

Источник

Линия тока и элементарная струйка

ОСНОВЫ ГИДРОДИНАМИКИ

КИНЕМАТИКА ЖИДКОСТИ

Раздел гидромеханики, изучающий движение жидкости, а также взаимодействие между жидкостью и твердыми телами при их относитель­ном движении, называется гидродинамикой.

Раздел гидро­механики, изучающий кинематические характеристики (скорости и ускорения) движения в потоках жидкости и их изменение во времени, называется кинематикой жидкости.

Принимают, что жидкость представляет собой сплошную среду и все кинематические характеристики непрерывны в пространстве и времени.

Закономер­ности кинематики справедливы для невязких и вязких жидкостей.

Формы движения жидкости, встречающиеся в природе и технике, весьма разнообразны. Сложность изучения течений жидкости обусловлена тем, что поток представляет собой деформируемую среду.

Понятие об установившемся и неустановившемся движении жид­кости

Поток жидкости представляет собой движущуюся массу жид­кости. Скорости в разных точках пространства, занятого движущейся жидкостью, имеют разное значение, что объясняется влиянием поверх­ностей, ограничивающих поток. Изменяются в потоке и направления скоростей.

Обозначим скорость в точке через и, а её проекции на оси координат и_х, u_y, и_z.

Движение жидкости, при котором её скорость в любой точке заня­того жидкостью пространства не изменяется во времени, называется установившимся движением.

Другими словами, проекции скоростей есть функции только координат х, у, z,

На основании этого определения, частные производные от и_х, и_у, и_z по t равны нулю:

Примерами установившегося движения могут служить:

— истечение жидкости через отверстие в баке при постоянном в нем уровне;

— дви­жение воды в водопроводной трубе или канале с неизменной во времени скоростью течения и др.

Движение жидкости, при котором её скорость во всех точках заня­того жидкостью пространства изменяется по значению и (или) направлению во времени, называют неустановившемся дви­жением.

Примерами такой формы движения могут служить:

— движение воды в реках во время паводков;

— истечение жидкости через отверстие в баке при пе­ременном в нем уровне воды.

Линия тока и элементарная струйка

Геометрическое представле­ние о движении жидкости можно получить с помощью построения векторных линий, называемых линиями тока.

Линию, в каждой точкекоторой в данное мгновение вектор скорости жидкости совпадает с касательной к этой линии, называют линией тока.

При неустановившемся движении каждому моменту времени отвечает определенная система линий тока, вид и расположение которых харак­теризуют поле скоростей.

При установившемся движении значения и направления скоростей не изменяются с течением времени. Следова­тельно, линии тока должны совпадать в этом случае с траекториями движущихся частиц жидкости.

Линии тока не могут пересекаться.

Линии тока дают как бы фотографический снимок с картины распре­деления в жидкости векторов скоростей частиц.

Траектории дают представление о пути частиц жидкости в пространст­ве с течением времени, т.е. рисуют как бы историю движения частиц.

Поверхность, образованная линиями тока, проведенными через все точки какой-либо заданной линии, называют поверхностью тока.

Часть движущейся жидкости, ограниченная поверхностью тока, про­веденной в данное мгновение через все точки бесконечно малого замк­нутого контура (см. рис. 1), находящегося в области, занятой жид­костью, называют элементарной струйкой.

Через боковую поверхность элементарной струйки жидкость не перетекает.

В каждой точке поверхности, ограниченной бесконечно малым замк­нутым контуром, скорости направлены по нормалям и в пределах этой бесконечно малой поверхности принимаются одинаковыми.

Нормальное (поперечное) сечение элементарной струйки называют живым сечением элементарной струйки.

Площадь живого сечения может изменяться по длине струйки. При смещении частиц жидкости на величину dl за время dt(см. рис. 1) эту площадь можно принять одинаковой.

В этом случае объём жидкости равен:

dV = dωdl

Поделив dV на dtи введя обозначения:

dV / dt= dQ

dl / dt = и ,

dQ = иdω (1)

и— скорость в живом сечении элементарной струйки.

Объём жидкости, протекающей в единицу времени через живое

сечение, называют расходом жидкости (в данном случае элементарным).

При установившемся движении элементарный расход по длине струйки не изменяется.

Поэтому для двух сечений элемен­тарной стручки (см. рис.1) получим уравнение:

называемое гидравлическим уравнением неразрывности элементарной струйки.

,

т. е. скорости в различных сечениях струйки обратно пропорциональны площадям живых сечений.

Источник