Что такое число степеней свободы в статистике
Хотя вводные учебники могут вводить степени свободы в качестве параметров распределения или посредством проверки гипотез, именно основная геометрия определяет степени свободы и имеет решающее значение для правильного понимания концепции.
СОДЕРЖАНИЕ
История
Обозначение
Случайных векторов
Геометрически степени свободы можно интерпретировать как размерность определенных векторных подпространств. В качестве отправной точки предположим, что у нас есть выборка независимых нормально распределенных наблюдений,
Это можно представить в виде n- мерного случайного вектора :
В приложениях статистического тестирования часто напрямую интересуют не составляющие векторы, а их квадрат длины. В приведенном выше примере остаточная сумма квадратов равна
В моделях структурных уравнений
Было показано, что читатели статей, содержащих SEM, могут использовать степени свободы, чтобы определить, действительно ли авторы этих статей сообщают правильную статистику соответствия модели. В организационных науках, например, почти половина статей, опубликованных в ведущих журналах, сообщают о степенях свободы, которые несовместимы с моделями, описанными в этих статьях, оставляя читателя гадать, какие модели были фактически протестированы.
Остатков
Пример
Икс ¯ п знак равно Икс 1 + ⋯ + Икс п п <\ displaystyle <\ overline
быть «выборочным средним». Тогда величины
вынуждены лежать в пространстве, определяемом двумя уравнениями
В линейных моделях
Наблюдения можно разложить как
В дисперсионном анализе (ANOVA)
В задачах статистического тестирования обычно интересуют не сами составляющие векторы, а их квадрат длины или сумма квадратов. Степени свободы, связанные с суммой квадратов, являются степенями свободы соответствующих составляющих векторов.
с 2 степенями свободы. Остаточная сумма квадратов, или ошибка, равна
В некоторых сложных настройках, таких как несбалансированные планы с разделением графиков, суммы квадратов больше не имеют масштабированного распределения хи-квадрат. Сравнение суммы квадратов со степенями свободы больше не имеет смысла, и в этих случаях программное обеспечение может сообщать об определенных дробных «степенях свободы». Такие числа не имеют подлинной интерпретации степеней свободы, а просто обеспечивают приблизительное распределение хи-квадрат для соответствующей суммы квадратов. Детали таких приближений выходят за рамки этой страницы.
В вероятностных распределениях
В нестандартной регрессии
Регрессионные эффективные степени свободы
Остаточные эффективные степени свободы
Общий
Другие составы
Что такое число степеней свободы в статистике?
Как определять число степеней свободы?
Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Что называется числом степеней свободы?
Числом степеней свободы материального объекта называют число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета.
Что такое степени свободы математическая статистика?
Сколько степеней свободы у человека?
Рука человека имеет 7 степеней свободы. Механическая система, имеющая 6 физических степеней свободы, называется голономной. Если система имеет меньшее количество степеней свободы, то её называют неголономной.
Чему равно число степеней свободы двухатомной молекулы?
Что показывает число степеней свободы k?
Иными словами, количество степеней свободы показывает размерность вектора из случайных величин, количество «свободных» величин, необходимых для того, чтобы полностью определить вектор.
Почему 6 степеней свободы?
Поскольку движение вдоль каждой из трёх осей не зависит от движения по остальным двум и вращения вокруг любой из осей, движение действительно имеет 6 степеней свободы.
Чему равно число степеней свободы тела с одной закрепленной точкой?
Движение твердого тела с одной неподвижной точкой –
это движение, при котором одна точка тела закреплена (три степени свободы).
Сколько степеней свободы имеют суставы Ода человека?
Как известно, тело, ничем не ограниченное в движениях, называется свободным, так как может двигаться в любом направлении. Отсюда, каждое свободное твердое тело имеет шесть степеней свободы движения.
Какая степень свободы у воздуха?
Первоначально было предложено пять «свобод воздуха»: две в отношении полетов воздушных судов и три в отношении перевозок. Три свободы, связанные с перевозками, а именно «третья», «четвертая» и «пятая» свободы охватывают полный перечень возможностей осуществления международных перевозок по воздуху.
Что такое степень свободы в термодинамике?
Какая степень свободы у азота?
Re: Определить кинетическую энергию
i – число степеней свободы. 1) Определим кинетическую энергию, приходящуюся в среднем на одну степень свободы молекулы азота (i = 1):
Какой суставы имеют 3 степени свободы?
К многоосным суставам с тремя степенями свободы принадлежат шаровидные, чашеобразные и плоские суставы.
Сколько степеней свободы у суставов?
Сколько степеней свободы в лучезапястном суставе?
И две степени свободы даёт лучезапястный сустав.
Число степеней свободы.



Число степеней свободы (n) – это число свободно варьирующих единиц в составе выборки. Оно равно числу классов вариационного ряда минус число условий, при которых он был сформирован. К числу таких условий относятся объём выборки (n), средние и дисперсии.
Число степеней свободы у выборочного ряда определяется:
n = n – 1, где n – общее число элементов ряда (выборки).
При наличии не одного, а нескольких ограничений свободы вариации, число степеней свободы определяется по формуле:
ν = n – k, где k – число ограничений свободы вариации.
Для таблицы экспериментальных данных число степеней свободы определяется следующим образом:
ν = (c – 1) (n – 1), где c – число столбцов, а n – число строк таблицы (число испытуемых).
Для ряда статистических методов подсчёт числа степеней свободы оказывается необходимым и рассчитывается по-своему.
Понятие нормального распределения.
В статистике под рядом распределения понимают распределение частот по вариантам. Распределением признака называется закономерность встречаемости разных его значений.
Особое место в статистике занимает нормальное распределение. График нормального распределения представляет собой колоколообразную кривую. Форма и положение графика определяется только двумя параметрами: средней (µ) и стандартным отклонением (σ).
Для нормального распределения характерно совпадение величин средней арифметической, моды и медианы. Равенство этих показателей указывает на нормальность данного распределения.
Ещё одна особенность нормального распределения: чем больше величина признака отклоняется от среднего значения, тем меньше буде частота встречаемости (вероятность) этого признака в распределении. «Нормальным» распределение названо потому, что оно наиболее часто встречалось в естественнонаучных исследованиях и казалось «нормой» распределения случайных величин.
| -4σ |
| -3σ |
| -2σ |
| -σ |
| μ σ 2σ 3σ 4σ |
В психологии нормальное распределение используется при разработке и применении тестов интеллекта и способностей. Для показателей интеллекта IQ нормальное распределение имеет µ = 100, а σ = 16 для большинства возрастных групп.
Однако, для других психологических категорий (личностная и мотивационная сфера) применение нормального распределения оказывается дискуссионным.
При нормальном распределении экспериментальных данных применяются особые методы статистической обработки.
Кроме нормального существуют и другие распределения. При обработке экспериментальных данных целесообразно проводить оценку характера распределения. Это поможет решить вопрос о возможности применения того или иного статистического метода.
Вопросы для обсуждения
1. Мода и правила её нахождения. Какая выборка называется мономодальной, бимодальной, полимодальной?
2. Что можно назвать модой признака «оценка за экзамен в последнюю сессию» в вашей группе?
3. Медиана и правила её нахождения.
3. Среднее арифметическое, взвешенная средняя. Преимущества и недостатки средних значений при характеристике выборки.
4. Разброс выборки. Связь между размахом выборки и силой варьирования признака.
5. Дисперсия и стандартное отклонение. Их смысл и правила вычисления.
6. Число степеней свободы и правила его вычисления.
7. Распределение признака. Ряд распределения.
8. Нормальное распределение, его особенности. Распространённость нормального распределения в психологии.
ТЕМА №4. Общие принципы проверки статистических гипотез.
Степени свободы (теория вероятностей)
Количество степеней свободы может быть не только натуральным, но и любым действительным числом, хотя стандартные таблицы рассчитывают p-value наиболее распространённых распределений только для натурального числа степеней свободы.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Модели дискретного выбора — экономические (эконометрические) модели, позволяющие описывать, объяснять и прогнозировать выбор между, двумя или более альтернативами (то есть когда множество альтернатив не более чем счетно). Модели дискретного выбора позволяют на основе некоторых характеристик (атрибутов) экономического субъекта или ситуации оценить вероятность выбора той или иной альтернативы.
В статистике метод оценки с помощью апостериорного максимума (MAP) тесно связан с методом максимального правдоподобия (ML), но дополнительно при оптимизации использует априорное распределение величины, которую оценивает.
В теории представлений групп Ли и алгебр Ли, фундаментальное представление — это неприводимое конечномерное представление полупростой группы Ли или алгебры Ли, старший вес которого является фундаментальным весом. Например, определяющий модуль классической группы Ли является фундаментальным представлением. Любое конечномерное неприводимое представление полупростой группы Ли или алгебры Ли полностью определяется своим старшим весом (теорема Картана) и может быть построено из фундаментальных представлений.
Максимальным идеалом коммутативного кольца называется всякий собственный идеал кольца, не содержащийся ни в каком другом собственном идеале.
О степенях свободы в статистике
В одном из предыдущих постов мы обсудили, пожалуй, центральное понятие в анализе данных и проверке гипотез — p-уровень значимости. Если мы не применяем байесовский подход, то именно значение p-value мы используем для принятия решения о том, достаточно ли у нас оснований отклонить нулевую гипотезу нашего исследования, т.е. гордо заявить миру, что у нас были получены статистически значимые различия.
Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.
Степени свободы, о чем речь?
По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.
Давайте рассмотрим пример небольшого статистического исследования, чтобы понять, зачем нам нужен показатель df, и в чем же с ним такая проблема. Допустим, мы решили проверить гипотезу о том, что средний рост жителей Санкт-Петербурга равняется 170 сантиметрам. Для этих целей мы набрали выборку из 16 человек и получили следующие результаты: средний рост по выборке оказался равен 173 при стандартном отклонении равном 4. Для проверки нашей гипотезы можно использовать одновыборочный t-критерий Стьюдента, позволяющий оценить, как сильно выборочное среднее отклонилось от предполагаемого среднего в генеральной совокупности в единицах стандартной ошибки:
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:

Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.
Но почему n минус один?
Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?
В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:
“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?
Причем тут распределение Хи-квадрат Пирсона?
Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:
имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.
Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?
Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:
Где O — наблюдаемые, E — ожидаемые частоты.
Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.
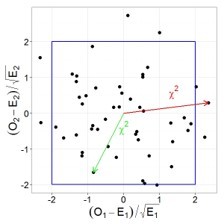
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:
При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.
Пришло время вычесть единичку!
Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.

Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.
Все становится на свои места
Теперь, вооружившись этими знаниями, вернемся к t-тесту:
в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.
Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.
Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.
Онлайн курсы по статистике: объясняем сложные темы простым языком
Стоит также отметить, что теоретические знания в области статистики будут определенно полезны не только тем, кто применяет статистику в академических целях, но и для тех, кто использует анализ данных в прикладных областях. Базовые знания в области статистики просто необходимы для освоения более сложных методов и подходов, которые используются в области машинного обучения и Data Mining. Таким образом, успешное прохождение наших курсов по введению в статистику — хороший старт в области анализа данных. Ну а если вы всерьез задумались о приобретении навыков работы с данными, думаем, вас может заинтересовать наша онлайн — программа по анализу данных, о которой мы подробнее писали здесь. Упомянутые курсы по статистике являются частью этой программы и позволят вам плавно погрузиться в мир статистики и машинного обучения. Однако пройти эти курсы без дедлайнов могут все желающие и вне контекста программы по анализу данных.