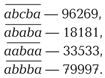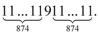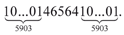Что такое числа палиндромы
Палиндромами так же являются квадраты таких чисел, как 11, 111, 1111 и т д. А именно:
11112 = 1 234 321 и т. д.
Интересно! что
1 + 2 + 1 = 4 = 2(во 2степени)
1 + 2 + 3 + 2 + 1 = 9 = 3(во 2степени)
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 = 4(во 2степени)
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25 = 5(во 2степени)
Каждое из подобных чисел, можно изложить в виде неправильных дробей:
121=22х22/1+2+1
12321 =333х333/1+2+3+2+1
1234321=4444х4444/1+2+3+4+3+2+1
и так далее.
Наконец, для деления получаем:
82:41=28:14
62:31=26:13
— произведение первой цифры числа N1 на вторую цифру числа N2 равно произведению двух других их цифр: х1.у 2 = х2.у 1 (вы заметили связь между примерами на деление и умножение?).
https://www.nkj.ru/archive/articles/10656/
Особенно наглядно свойственное палиндрому «вечное движение» (вращение) проявляется в циклических палиндромах, или круговертнях, то есть в текстах, одинаково читаемых в обе стороны, но уже при записи вдоль окружности:
Еще одной разновидностью палиндрома является монопалиндром (термин А. Бубнова), т. е. единый палиндромный текст, записанный в несколько строк:
1. ортогонал: друг // враг (С. Ф.)
(Иллюстрация 2)
2. опрокидень: Звезда // звезда (Д. Авалиани)
(Иллюстрация 3)
3. опрокидень: Ты Бог // гад ты (С. Ф.)
(Иллюстрация 4)
В свою очередь наиболее перспективным из этих двух подвидов поворотня представляется опрокидень. Во всяком случае, примеров опрокидней известно на порядок больше, нежели ортогоналов. Поэтому заострим свое внимание именно на них.
Уже из приведенных выше примеров становятся видны принципиальные отличия опрокидня от палиндрома.
Во-первых, палиндромные строчки объективны и практически не зависят от индивидуальности автора. Поэтому-то так часты пересечения у любителей палиндромов. Опрокидни же сугубо индивидуальны, интимны, целиком зависят от почерка и фантазии автора:
1. Совсем я плох // хочу в народ.
(Иллюстрация 5)
2. Нимфа // вернись
(Иллюстрация 6)
3. Вернись // никогда (Д. Авалиани).
https://www.nkj.ru/archive/articles/10480/
Простейшие слова-палиндромы: мим, дед, наган, заказ, кабак, казак, мадам, шалаш. Самое длинное слово-палиндром, существительное, содержит 7 букв — ротатор. А если не требовать именительного падежа и единственного числа, то рекордсменом будет слово манекенам.
Будущие, ищу дуб,
Но сила ли сон?
* * *
Иль обида ради боли?
Доктор геолого-минералогических наук, кандидат физико-математических наук Б. ГОРОБЕЦ отмечает, что в русских палиндромах неизменно нечетное количество букв
https://www.nkj.ru/archive/articles/538/
Первый неожиданный результат был получен при частотном анализе распределения слов по числу букв. Почти все слова-палиндромы русского языка насчитывают нечетное число букв, от 1 до 11 (синие линии на гистограмме). Ничего подобного нет среди обычных, то есть несимметричных, слов (красные линии на гистограмме, демонстрирующие частотность слов, взятой из Частотного словаря русского языка, 1977, с.930). Гистограммы различаются настолько разительно, что нет смысла приводить математические выкладки по проверке статистической гипотезы о значимости указанного различия. Хотя сделать это несложно, и можно показать, что риск ошибки в сделанном выводе не превышает 0,01%.
Итак, «закон нечетности» распространяется исключительно на буквенно-симметричные словоформы, то есть на палиндромы! Однако, разумеется, это утверждение требует более строгой математико-лингвистической проверки путем подсчета слов со сдвоенным центром, имеющих как четное, так и нечетное число букв.
Замечательно, что действие «закона нечетности» распространяется не только на слова, но и на палиндромные фразы и более сложные тексты. Случайная выборка из 114 фраз у 33 авторов показала, что их доля с четным числом букв составляет 12,3%. У классика жанра Д. Авалиани она равна 13,5% в выборке из 200 фраз. Отсюда средняя доля центро-симметричных фраз, то есть фраз с центральной буквой, близка к 88% (тоже, кстати, цифровой палиндром!).
Естественен вопрос: а для чего все это нужно? Законы словообразования (если они действительно законы, выраженные количественно) действуют специфично и объективно на данное множество элементов, помогают формировать ту научную базу данных, которая необходима для создания и совершенствования новых информационных технологий, в частности кодирования и декодирования сообщений, переводов, распознавания образов (слов, слогов) в сигнале на фоне шума. И здесь нужны сведения о частотности слов в речи и литературе различных стилей. Эту работу еще предстоит выполнить.
Амфирифма
Сологолос
(В. Рыбинский)
Анархоохрана
Микрозорким
Маревоверам
Суперэпус
Синепенис
Трах-арт
Тревыверт
(В. Гершуни)
Лохохохол
(Джети
Автоботва
Аквалавка
Пракарп
Ретропортер
(Б. Гринберг)
Оленинело
(Ю. Телесин)
Девовед
Монгологном
Мордодром
(В. Хромов)
Икотопотоки
(Л. Адрианов)
Артсестра
Иноони
(Г. Лукомников)
Коненок
(К. Соприцкий)
Киторотик
(П. Нагорских)
Речевечер
(С. Красовицкий)
МакроЛоркам
МикроГорьким
Сотанатос
Солововолос
(С. Федин)
Тревоговерт
(Д. Минский)
Китокотик
Лифонофил (лифон жарг.- лифчик)
Недороден
Ротомотор
(Б. Горобец)
Конещенок
Недеееден
(Б. Гольдштейн)
Палиндромы и «перевёртыши» среди простых чисел
Числовой палиндром — это натуральное число, которое читается слева направо и справа налево одинаково. Иначе говоря, отличается симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным. Палиндромы встречаются в некоторых множествах чисел, удостоенных собственных названий: среди чисел Фибоначчи — 8, 55 (6-й и 10-й члены одноимённой последовательности); фигурных чисел — 676, 1001 (квадратное и пятиугольное соответственно); чисел Смита — 45454, 983389. Указанным свойством обладает также всякий репдиджит, например 2222222 и, в частности, репьюнит*.
Палиндром можно получить как результат операций над другими числами. Так, в книге «Есть идея!» известного популяризатора науки Мартина Гарднера в связи с этой задачей упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с обращённым числом, то есть записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не образуется палиндром. Иногда достаточно сделать всего один шаг (например, 312 + 213 = 525), но, как правило, требуется не менее двух. Скажем, число 96 порождает палиндром 4884 только на четвёртом шаге. В самом деле:
А суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.
Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:
До сих пор мы рассматривали в основном составные числа. Теперь обратимся к числам простым. В их бесконечном множестве имеются немало любопытных экземпляров и даже целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходятся на первую тысячу, из них четыре числа однозначные — 2, 3, 5, 7 и всего одно двузначное — 11. С такими числами связано немало интересных фактов и красивых закономерностей.
Во-первых, существует единственный простой палиндром с чётным числом цифр — 11. Другими словами, произвольный палиндром с чётным числом цифр, бóльшим двух, число составное, что нетрудно доказать на основе признака делимости на 11.
Во-вторых, первой и последней цифрами любого простого палиндрома могут быть только 1, 3, 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Любопытно, что все простые двузначные числа, записанные с помощью перечисленных цифр (за исключением 19), можно разбить на пары чисел-«перевёртышей» (взаимно обращённых чисел) вида 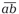
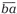
Заглянув в таблицу простых чисел, мы обнаружим аналогичные пары, в записи которых присутствуют и другие цифры, в частности, среди трёхзначных чисел подобных пар наберётся четырнадцать.
Кроме того, среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1:
Аналогичная картина наблюдается и у бо`льших простых чисел, например:
Простые числа-палиндромы могут «задаваться» разными симметричными формулами, которые отражают особенности их записи. Это хорошо видно на примере пятизначных чисел:
Кстати, простые многозначные числа вида 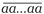
Вообще среди простых чисел-палиндромов встречаются удивительные экземпляры. Вот лишь один пример — числовой гигант
А интересен он тем, что содержит 11 811 цифр, которые можно разбить на три палидромические группы, причём в каждой группе количество цифр выражается простым числом (5903 или 5).
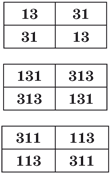
Любопытные палиндромические закономерности просматриваются и в группах простых чисел, в записи которых присутствуют определённые цифры. Скажем, только цифры 1 и 3, причём в каждом числе. Так, двузначные простые числа составляют упорядоченные пары 13 — 31 и 31 — 13, из шести трёхзначных простые сразу пять чисел, среди которых есть два палиндрома: 131 и 313, а ещё два числа образуют пары «перевёртышей» 311 — 113 и 113 — 311. Во всех этих случаях составленные пары наглядно представляются в виде числовых квадратов (рис. 1).
Своими свойствами они напоминают магический и латинский квадраты. Например, у среднего квадрата сумма чисел, стоящих в каждой строке и в каждом столбце, равна 444, на диагоналях — 262 и 626. Сложив числа из всех клеток, получим 888. И что характерно, каждая сумма — палиндром. Даже просто выписывая без пробела несколько чисел из одной таблицы, получим новые палиндромы: 3113, 131313131 и т. д. Какое наибольшее число можно составить таким способом? Будет ли оно палиндромом?
Если в каждую из пар 311 — 113 и 113 — 311 добавить 131 или 313, образуются четыре палиндромические тройки. Запишем одну из них в столбик:
Как видим, и сами числа, и нужная их комбинация дают о себе знать при прочтении в разных направлениях. Кроме того, расположение цифр симметрично, а их сумма в каждой строке, каждом столбце и на одной из диагоналей выражается простым числом − 5.
Надо сказать, рассмотренные числа интересны и сами по себе. Например, палиндром 131 — простое циклическое число: при любых последовательных перестановках первой цифры на последнее место он порождает простые числа 311 и 113. Можете ли вы указать другие простые палиндромы, обладающие таким же свойством?
А вот пары чисел-«перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:
(1 + 1 + 3) 2 = 1 + 2 + 7 + 6 + 9.
Добавим, что среди натуральных чисел имеются и другие пары «перевёртышей» с подобным свойством: 103 — 301, 1102 — 2011, 11113 — 31111 и др. Чем объясняется подмеченная закономерность? Чтобы ответить на этот вопрос, нужно понять, что особенного в записи указанных чисел, какие цифры и в каком количестве могут в ней присутствовать.
Из простых чисел-палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
Вот, например, красивая комбинация из простых палиндромов, записанных с помощью 1 и 3 (кроме первого, рис. 2). Особенность этого числового треугольника в том, что один и тот же фрагмент повторяется трижды, не нарушая симметрию рисунка.
Легко видеть, что общее количество строк и столбцов — число простое (17). К тому же простые числа и суммы цифр: выделенных красным фрагментов (17); каждой строки, за исключением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и девятого столбцов (7, 11) и «лесенки» из единиц, образующей боковые стороны треугольника (11). Наконец, если двигаться параллельно указанным «сторонам» и складывать по отдельности цифры третьего и пятого рядов (рис. 3), получим ещё два простых числа (17, 5).
Продолжая построение, можно сконструировать на основе данного треугольника более сложные фигуры. Так, ещё один треугольник с аналогичными свойствами нетрудно получить, двигаясь с конца, то есть начать с последнего числа, вычёркивая на каждом шаге две одинаковые симметрично расположенные цифры и переставляя или заменяя другие — 3 на 1 и наоборот. При этом сами цифры следует выбирать с таким расчётом, чтобы образующееся в итоге число оказалось простым. Объединив обе фигуры, получим ромб с характерным узором из цифр, скрывающим в себе немало простых чисел (рис. 4). В частности, сумма выделенных красным цветом цифр равна 37.
Другой пример — треугольник, полученный из исходного после добавления к нему шести простых палиндромов (рис. 5). Фигура сразу привлекает внимание своим изящным обрамлением из единиц. Её окаймляют два простых репьюнита одинаковой длины: 23 единицы составляют «основание» и ещё столько же — «боковые стороны» треугольника.
Ещё несколько фигур
Можно составить также многоугольные фигуры из чисел, обладающие определёнными свойствами. Пусть требуется построить фигуру из простых палиндромов, записанных с помощью 1 и 3, у каждого из которых крайние цифры — единицы, а сумма всех цифр и общее количество единиц в строке — простые числа (исключение — однозначный палиндром). Кроме того, простым числом должно выражаться общее количество строк, а также цифр 1 либо 3, встречающихся в записи.
На рис. 6 приведено одно из решений задачи — «домик», сконструированный из 11 различных палиндромов.
Конечно, не обязательно ограничиваться двумя цифрами и требовать наличия в записи каждого используемого числа всех указанных цифр. Скорее, наоборот: ведь именно их необычные сочетания придают своеобразие узору фигуры. В подтверждение этому приведём несколько примеров красивых палиндромических зависимостей (рис. 7−9).
Теперь, вооружившись таблицей простых чисел, вы и сами сконструируете фигуры вроде предложенных нами.
А напоследок ещё одна диковинка — треугольник, буквально пронизанный вдоль и поперёк палиндромами (рис. 10). В нём 11 строк из простых чисел, а столбцы образованы репдиджитами. И главное: ограничивающий фигуру с боков палиндром 193111111323111111391 — число простое!
Комментарии к статье
*Число Смита — составное число, сумма цифр которого равна сумме цифр его простых делителей.
Репдиджит — натуральное число, в записи которого все цифры одинаковые.
Репьюнит — натуральное число, записанное с помощью одних только единиц.
Что такое числа палиндромы
Назовем исходное число и число с переставленными в обратном порядке цифрами взаимно обратными.
Выяснено, что сложение некоторых взаимно обратных чисел приводит к образованию числа-палиндрома. Но для многих взаимно обратных чисел такое число палиндром при сложении не образуется. А что будет, если в этом случае сложить результат сложения с его взаимно обратным числом?
Задание:
Как зависит результат сложения от суммы цифр исходного числа?
Ответ можешь посмотреть здесь.
Примерами являются все однозначные числа, двузначные вида αα, такие как 11 и 99, трехзначные числа вида αβα, например 535 и так далее.
Слово палиндром произошло от греческого слова palindromos ( palнndromos ) , обозначающего “вновь бегущий назад”. Палиндромами могут быть не только числа, но также и слова, предложения и даже тексты. Примером может служить слова ротор, радар или известная фраза “А роза упала на лапу Азора”, которые читаются одинаково как слева направо, так и справа налево. В английском языке это слова «Radar», «I», «Eve», «Deed, «Redivider» и фразы «Madam, I’m Adam, «A man, a plan, a canal. Panama «. Примеры палиндромов встречаются и в природе – молекула ДНК, например, имеющая комплиментарные основания. В ДНК есть отрезки, имеющие одинаковую нуклеотидную последовательность при чтении по обеим цепям спирали в одинаковом направлении. Общее число таких «перевертышей» в геноме человека оценено от 100 тыс. до 1 млн. При этом они относительно равномерно распределены по ДНК.
Греческие поэты еще в 300 году до н.э. начали употреблять палиндромы.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202,… (последовательность A002113 в OEIS ).
СОДЕРЖАНИЕ
Формальное определение
причем, как обычно, 0 ≤ a i Десятичные палиндромные числа
Все числа в базе 10 (и действительно в любой базе) с одной цифрой являются палиндромными, поэтому существует десять десятичных палиндромных чисел с одной цифрой:
Всего существует 9 палиндромных чисел с двумя цифрами:
Существует 90 палиндромных чисел с тремя цифрами (Использование правила произведения : 9 вариантов выбора для первой цифры, которая также определяет третью цифру, умноженных на 10 вариантов для второй цифры):
Также существует 90 палиндромных чисел с четырьмя цифрами (опять же, 9 вариантов выбора для первой цифры, умноженные на десять вариантов для второй цифры. Две другие цифры определяются выбором первых двух):
Ниже 10 5 находится 1099 палиндромных чисел, а для других показателей степени 10 n мы имеем: 1999, 10999, 19999, 109999, 199999, 1099999,… (последовательность A070199 в OEIS ). Количество палиндромных чисел, обладающих некоторыми другими свойствами, перечислено ниже:
Совершенные силы
Г. Дж. Симмонс предположил, что не существует палиндромов формы n k для k > 4 (и n > 1).
Другие базы
или в десятичном виде:
В простых числах Ферма и простые числа Мерсены образуют подмножество двоичных палиндромных простых чисел.
| 13 2 | знак равно | 202 |
| 26 2 | знак равно | 1111 |
| 55 2 | знак равно | 4444 |
| 101 2 | знак равно | 10201 |
| 143 2 | знак равно | 24442 |
В основании 18 некоторые степени семи являются палиндромными:
| 7 0 | знак равно | 1 |
| 7 1 | знак равно | 7 |
| 7 3 | знак равно | 111 |
| 7 4 | знак равно | 777 |
| 7 6 | знак равно | 12321 |
| 7 9 | знак равно | 1367631 |
И в базе 24 первые восемь степеней пяти также являются палиндромными:
| 5 0 | знак равно | 1 |
| 5 1 | знак равно | 5 |
| 5 2 | знак равно | 11 |
| 5 3 | знак равно | 55 |
| 5 4 | знак равно | 121 |
| 5 5 | знак равно | 5A5 |
| 5 6 | знак равно | 1331 |
| 5 7 | знак равно | 5FF5 |
| 5 8 | знак равно | 14641 |
| 5 А | знак равно | 15AA51 |
| 5 С | знак равно | 16FLF61 |
Lychrel процесс
Непалиндромные числа можно соединить с палиндромными числами с помощью ряда операций. Во-первых, непалиндромное число меняется на противоположное, и результат прибавляется к исходному числу. Если результатом не является палиндромное число, это повторяется до тех пор, пока не будет получено палиндромное число. Такой номер называется «отложенным палиндромом».
Сумма обратных
Числа Шахерезады
Суммы палиндромов
В 2018 году была опубликована статья, демонстрирующая, что каждое положительное целое число можно записать как сумму трех палиндромных чисел в каждой системе счисления с основанием 5 или больше.
Палиндром чисел
Содержание
Палиндромы в десятичной системе счисления
Всего существует девять двузначных палиндромных чисел:
Всего существует 90 трехзначных чисел-палиндромов:
а также 90 четырехзначных палиндромных чисел:
Кроме того, каждое целое число, которое не делится на 10, имеет положительное кратное, которое является десятичным палиндромом, что должно было быть доказано в задании на Федеральном конкурсе математиков 2009 года.
Генерация числовых палиндромов
Возведение чисел в квадрат
В десятичной системе проходит
| 1 | * | 1 | знак равно | 1 |
| 11 | * | 11 | знак равно | 121 |
| 111 | * | 111 | знак равно | 12321 |
| 1111 | * | 1111 | знак равно | 1234321 |
| 11111 | * | 11111 | знак равно | 123454321 |
| 111111 | * | 111111 | знак равно | 12345654321 |
| 1111111 | * | 1111111 | знак равно | 1234567654321 |
| 11111111 | * | 11111111 | знак равно | 123456787654321 |
| 111111111 | * | 111111111 | знак равно | 12345678987654321 |
Инверсия и сложение
Другой возможностью является итерационная схема, в которой любое положительное число (которое само по себе не является палиндромом) вращается по следующему алгоритму, пока не достигнет палиндрома :
Палиндромы при преобразовании системы счисления
Числовые палиндромы также могут возникать при преобразовании десятичных чисел в другую систему счисления.
В следующей таблице перечислены все числовые палиндромы (для чисел от 10 до 10 7 ), которые являются результатом преобразования десятичной системы счисления в соответствующую систему счисления.
| База | десятичное число | Число в другой системе счисления |
|---|---|---|
| 4-й | 13 | 31 год |
| 7-е | 23 | 32 |
| 46 | 64 | |
| 2116 | 6112 | |
| 15 226 | 62 251 | |
| 8 ( восьмеричный ) | 1,527,465 | 5 647 251 |
| 9 | 445 | 544 |
| 313,725 | 527,313 | |
| 3 454 446 | 6 444 543 | |
| 12 ( двенадцатеричный ) | 315,231 | 132 513 |
| 13 | 43 год | 34 |
| 86 | 68 | |
| 774 | 477 | |
| 14-е | 834 | 438 |
| 16 ( шестнадцатеричный ) | 53 | 35 год |
| 371 | 173 | |
| 5141 | 1415 | |
| 99 481 | 18 499 | |
| 19-е | 21-е | 12 |
| 42 | 24 | |
| 63 | 36 | |
| 84 | 48 | |
| 441 | 144 | |
| 882 | 288 | |
| 7721 | 1277 | |
| 9471 | 1749 | |
| 21-е | 551 | 155 |
| 912 | 219 | |
| 22-е | 73 | 37 |
| 511 | 115 | |
| 25-е | 83 | 38 |
| 28 | 31 год | 13 |
| 62 | 26-е | |
| 93 | 39 | |
| 961 | 169 | |
| 37 | 41 год | 14-е |
| 82 | 28 | |
| 46 | 51 | 15-е |
| 55 | 61 | 16 |
| 64 | 71 | 17-е |
| 73 | 81 год | 18-е |
| 82 | 91 | 19-е |
Сумма числа палиндромов
В эссе 2018 года было показано, что любое положительное целое число можно записать как сумму трех числовых палиндромов, независимо от используемой системы счисления с основанием 5 или более.