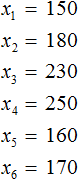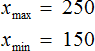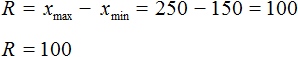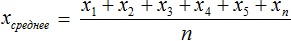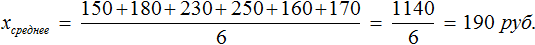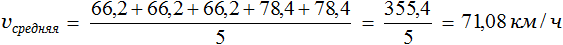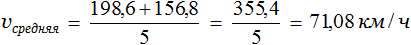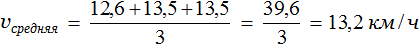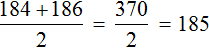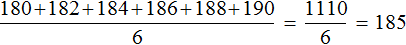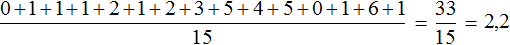Что такое частота выборки

Аналоговый ввод

Аналоговое и цифровое представление сигнала

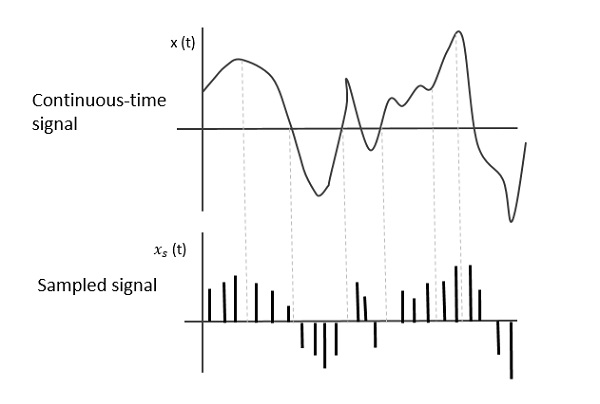
Следующий рисунок демонстрирует аналоговый сигнал и соответствующую ему оцифрованную версию. Выборки заданы в дискретные моменты времени.

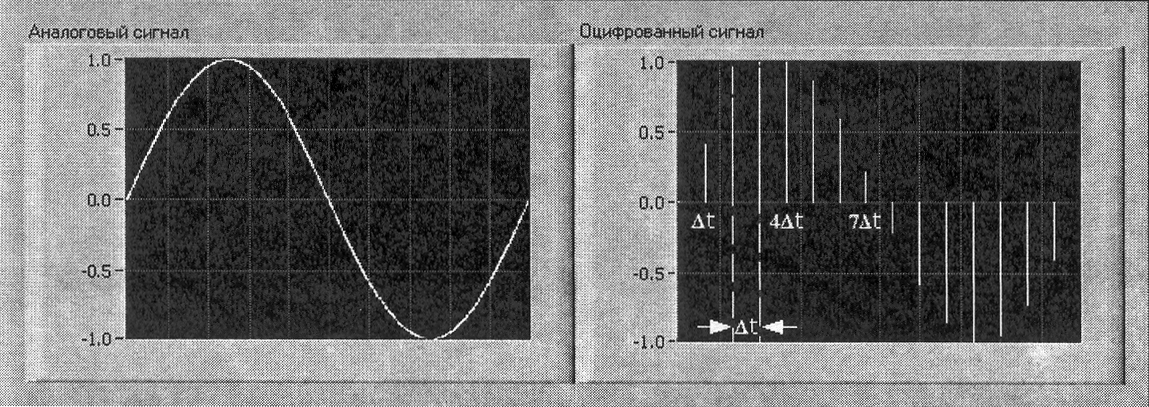Один из наиболее важных параметров измерительной системы с аналоговым вводом или выводом является частота, с которой измерительное устройство производит выборку входного сигнала или генерацию выходного. Частота сканирования или частота выборки в АЦП определяет, насколько часто имеет место аналого-цифровое или цифро-аналоговое преобразование. При большей частоте выборки собирается больше точек за данное время, что позволяет построить лучшее представление исходного сигнала, чем при низкой частоте выборки. Генерация одногерцового сигнала с использованием 1000 точек на период при частоте 1000 выборок в секунду создает гораздо более точное представление, чем использование 10 точек на период при частоте 10 Выб/сек.

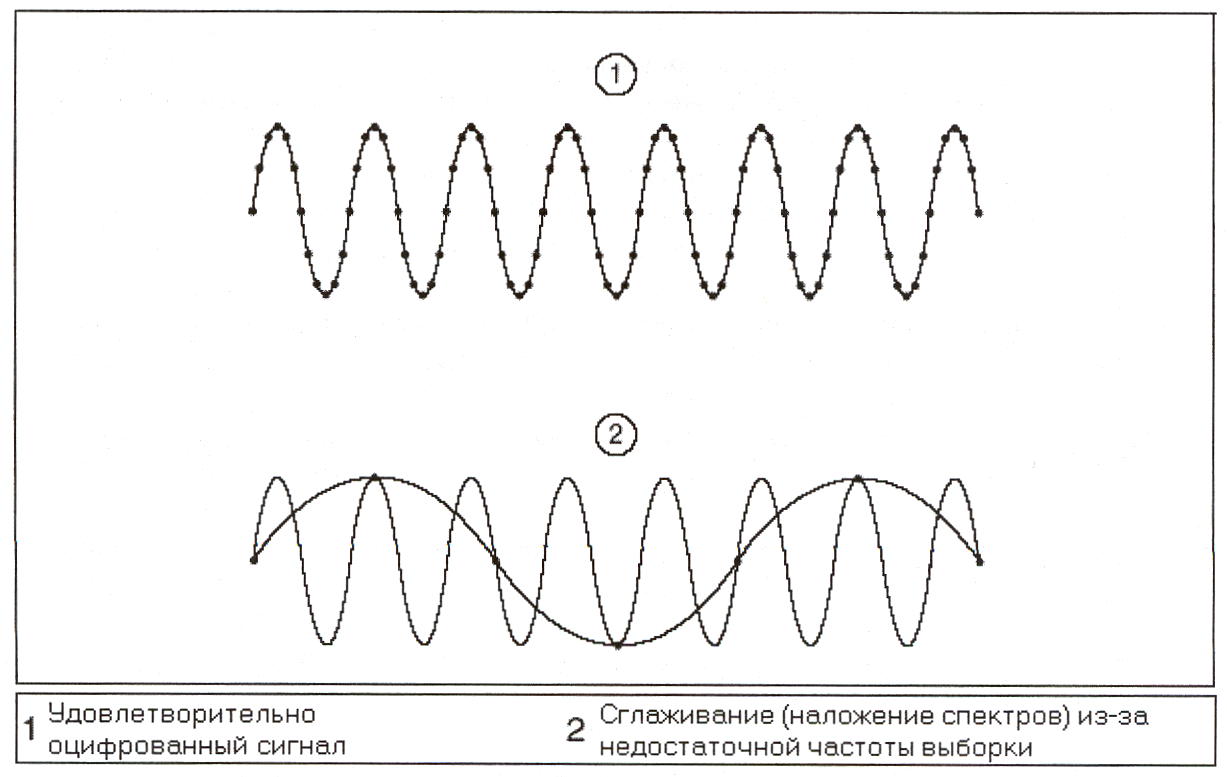
Слишком низкая частота выборки приводит к такому явлению, как наложение частот (aliasing), что вызывает искажение в представлении аналогового сигнала. Недостаточная скорость оцифровки является причиной того, что сигнал выглядит так, как будто его частота отлична от действительной. Чтобы избежать наложения частот оцифровку производят с частотой, большей частоты самого сигнала. Следующая иллюстрация показывает удовлетворительно оцифрованный сигнал и эффект наложения частот из-за недостаточной частоты выборки.

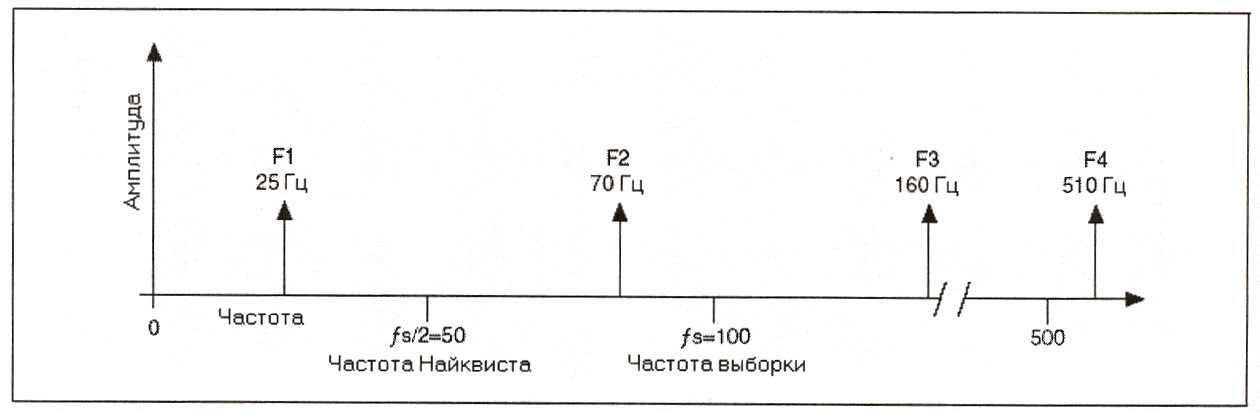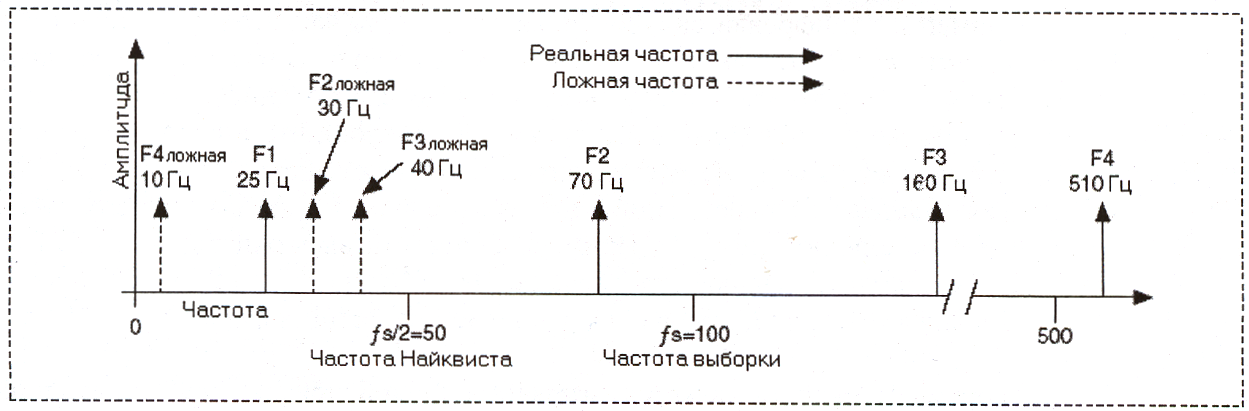
Частотные компоненты ниже частоты Найквиста (f_s/2 = 50 Гц) оцифровываются правильно. Это показано на следующей иллюстрации. Частотные компоненты выше частоты Найквиста появляются как побочные. Например, F₁ (25 Гц) появляется на правильной частоте, a F₂ (70 Гц), F₃ (160 Гц) и F₄ (510 Гц) имеют низкочастотные ложные компоненты на частотах 30 Гц, 40 Гц и 10 Гц, соответственно.

Определение частоты выборки

Возможно, вы захотите осуществлять выборку с максимально возможной частотой для данного измерительного устройства. Однако если вы оцифровываете очень быстро в течение длительных промежутков времени, то вам может не хватить оперативной памяти или дискового пространства для накопления данных. Следующая иллюстрация показывает влияние различных частот оцифровки на принимаемый сигнал.

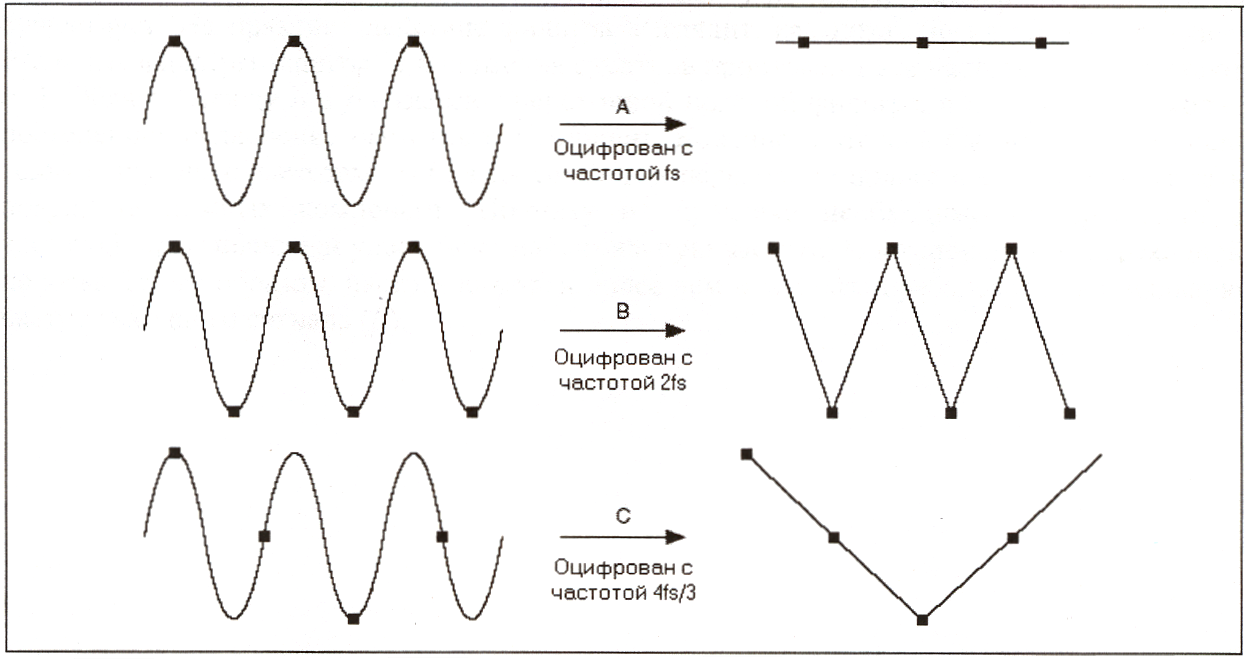Пример А: оцифровка синусоидального сигнала частотой f и с такой же частотой дискретизации f_s. В результате, полученные выборки образуют постоянный сигнал. Однако если вы увеличите частоту оцифровки до 2f_s, то оцифрованная осциллограмма будет иметь ту же частоту (или то же количество циклов), что и исходная осциллограмма, но будет выглядеть как треугольный сигнал, что показано на Примере В. Значительно увеличивая частоту дискретизации по сравнению с fs, вы можете более точно воспроизвести осциллограмму. В Примере С частота выборки равна 4f_s/3. Поскольку в этом случае частота Найквиста меньше f_s, (4f_s/3 х 1)/2 = 2f_s/3), то будет воспроизводиться осциллограмма с неправильной частотой и формой.

Источник

Цифровая связь — выборка

Выборка определяется как «Процесс измерения мгновенных значений непрерывного сигнала в дискретной форме».

Выборка — это фрагмент данных, взятый из целых данных, который непрерывен во временной области.

Когда источник генерирует аналоговый сигнал и если он должен быть оцифрован, имея 1 с и 0 с, то есть Высокий или Низкий, сигнал должен быть дискретизирован по времени. Эта дискретизация аналогового сигнала называется выборкой.

Частота выборки

S a m p l i n g F r e q u e n c y = f r a c 1 T s = f s

T s — время выборки

f s — частота выборки или частота выборки.

T s — время выборки

f s — частота выборки или частота выборки.

Для восстановления аналогового сигнала по оцифрованному сигналу частота дискретизации должна быть высоко оценена. Частота дискретизации должна быть такой, чтобы данные в сигнале сообщения не терялись и не перекрывались. Следовательно, ставка была фиксированной для этого, называемой скоростью Найквиста.

Рейтинг Найквиста

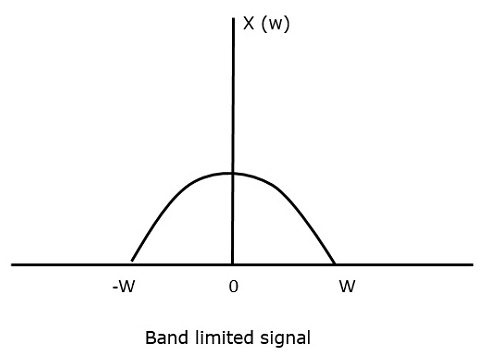
Предположим, что сигнал ограничен полосой частот без частотных составляющих выше, чем W герц. Это означает, что W — самая высокая частота. Для такого сигнала для эффективного воспроизведения исходного сигнала частота дискретизации должна быть в два раза выше самой высокой частоты.

f S — частота выборки

W самая высокая частота

f S — частота выборки

W самая высокая частота

Была сформулирована теорема под названием «Теорема выборки» о теории скорости Найквиста.

Теорема выборки

Теорема отсчетов гласит, что «сигнал может быть точно воспроизведен, если он дискретизируется с частотой f _s, которая в два раза превышает максимальную частоту W ».

Чтобы понять эту теорему отсчетов, давайте рассмотрим сигнал с ограниченной полосой частот, т. Е. Сигнал, значение которого не равно нулю между некоторыми значениями –W и W Герц.

Такой сигнал представляется как x ( f ) = 0 д л я | f l v e r t > W

Нам нужна частота выборки, частота, на которой не должно быть потери информации даже после выборки. Для этого у нас есть частота Найквиста, что частота дискретизации должна быть в два раза больше максимальной частоты. Это критическая частота выборки.

Если сигнал x (t) дискретизируется выше частоты Найквиста, исходный сигнал может быть восстановлен, а если он дискретизирован ниже частоты Найквиста, сигнал не может быть восстановлен.

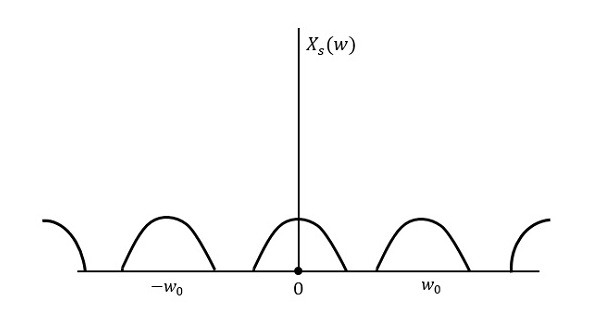
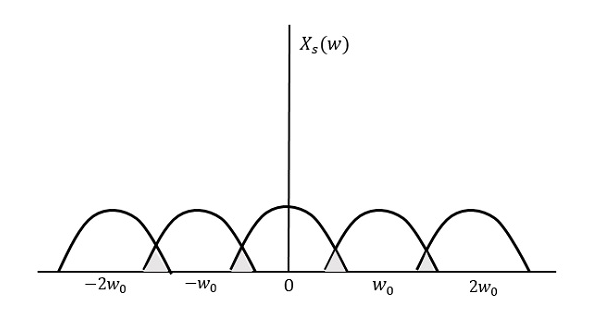
На следующем рисунке поясняется сигнал, если он дискретизируется с более высокой скоростью, чем 2 Вт в частотной области.

Преобразование Фурье сигнала x s ( t )

X s ( w ) = f r a c 1 T s s u m n = − i n f t y i n f t y X ( w − n w 0 )

Где T s = период выборки и w 0 = f r a c 2 p i T s

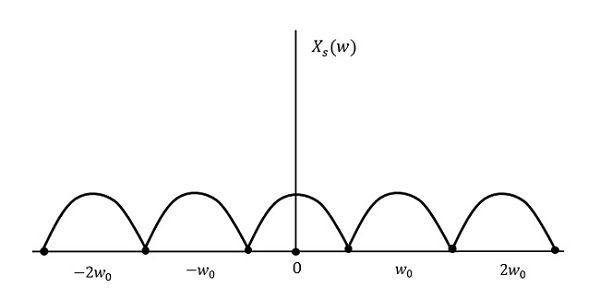
Давайте посмотрим, что произойдет, если частота дискретизации равна двойной максимальной частоте ( 2 Вт )

f s — частота выборки

W самая высокая частота

f s — частота выборки

W самая высокая частота

Результат будет таким, как показано на рисунке выше. Информация заменяется без каких-либо потерь. Следовательно, это также хорошая частота дискретизации.

Теперь давайте посмотрим на состояние,

Результирующий шаблон будет выглядеть следующим образом.

Из приведенного выше паттерна можно наблюдать, что происходит перекрытие информации, что приводит к смешению и потере информации. Это нежелательное явление перекрытия называется Aliasing.

Aliasing

Псевдоним может быть назван «явлением высокочастотного компонента в спектре сигнала, принимающего идентичность низкочастотного компонента в спектре его дискретизированной версии».

Корректирующие меры, принятые для уменьшения эффекта алиасинга, —

Сигнал, который дискретизируется после фильтрации, дискретизируется со скоростью, немного превышающей частоту Найквиста.

Сигнал, который дискретизируется после фильтрации, дискретизируется со скоростью, немного превышающей частоту Найквиста.

Этот выбор частоты дискретизации выше, чем частота Найквиста, также помогает упростить конструкцию фильтра восстановления в приемнике.

Область преобразования Фурье

Обычно наблюдается, что мы ищем помощи рядов Фурье и преобразований Фурье в анализе сигналов, а также в доказательстве теорем. Это потому что —

Преобразование Фурье является расширением ряда Фурье для непериодических сигналов.

Преобразование Фурье является мощным математическим инструментом, который помогает просматривать сигналы в разных областях и помогает легко анализировать сигналы.

Любой сигнал может быть разложен по сумме синусов и косинусов с использованием этого преобразования Фурье.

Преобразование Фурье является расширением ряда Фурье для непериодических сигналов.

Преобразование Фурье является мощным математическим инструментом, который помогает просматривать сигналы в разных областях и помогает легко анализировать сигналы.

Любой сигнал может быть разложен по сумме синусов и косинусов с использованием этого преобразования Фурье.

В следующей главе давайте поговорим о концепции квантования.

Источник

частота выборки

3.8 частота выборки (sampling frequency): Число выборочных значений сигнала в единицу времени (секунду) при записи или представлении сигнала в цифровом виде.

3.8 частота выборки (sampling frequency): Число выборочных значений сигнала в единицу времени (секунду) при записи или представлении сигнала в цифровом виде.

Полезное

Смотреть что такое «частота выборки» в других словарях:

частота выборки — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN sampling frequencysample rate … Справочник технического переводчика

частота выборки — ėmimo sparta statusas T sritis automatika atitikmenys: angl. sampling rate vok. Abtastrate, f; Tastdauer, f rus. частота выборки, f pranc. fréquence d échantillonnage, f … Automatikos terminų žodynas

частота — 3.2 частота: Вероятность появления последствия (возникновения опасного события). Источник: ГОСТ Р ИСО/ТС 14798 2003: Лифты, эскалаторы и пассажирские конвейеры. Методология анализа риска 06.01.15 частота [ frequency]: Число циклов периодического… … Словарь-справочник терминов нормативно-технической документации

частота (повторяемость) — 3.1.42 частота (повторяемость) (frequency): (статистическая) повторяемость события это число наблюдений события, возникающего при одной выборке. Частоты могут представляться графически в гистограммах. В настоящем стандарте частота (повторяемость) … Словарь-справочник терминов нормативно-технической документации

ЧАСТОТА — – число, показывающее сколько раз встречается в выборке каждая варианта. Сумма всех частот равна объему выборки [89, c. 173] … Современный образовательный процесс: основные понятия и термины

Частота относительная — доля или процент объектов, обладающих данным значением признака, по отношению к объему выборки … Социологический словарь Socium

Относительная частота реализаций эксперимента — Определение Пусть имеется некоторый реальный эксперимент и пусть через обозначен наблюдаемый в рамках этого эксперимента результат. Пусть произведено экспериментов, в которых результат может реализоваться или нет. И пусть это число реализаций… … Википедия

ТАКТОВАЯ ЧАСТОТА — (clock rate), число основных операций (циклов выборки и исполнения команд) компьютера (см. КОМПЬЮТЕР), производимых за 1 секунду. Измеряется в герцах (Hz, Гц; и их производных по системе СИ килогерцах, kHz, кГц, мегагерцах, MHz, МГц; гигагерцах,… … Энциклопедический словарь

Цветовая субдискретизация — (англ. Chroma subsampling) технология кодирования изображений со снижением цветового разрешения, при которой частота выборки цветоразностных сигналов может быть меньше частоты выборки яркостного сигнала. Основана на особенности человеческого … Википедия

Источник

Что такое частота выборки

1. Задачи математической статистики.

4. Статистическое распределение выборки.

5. Эмпирическая функция распределения.

6. Полигон и гистограмма.

7. Числовые характеристики вариационного ряда.

8. Статистические оценки параметров распределения.

9. Интервальные оценки параметров распределения.

1. Задачи и методы математической статистики

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным- контролируемый размер детали.

Иногда проводят сплошное исследование, т.е. обследуют каждый объект относительно нужного признака. На практике сплошное обследование применяется редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов (выборочную совокупность) и подвергают их изучению.

Основная задача математической статистики заключается в исследовании всей совокупности по выборочным данным в зависимости от поставленной цели, т.е. изучение вероятностных свойств совокупности: закона распределения, числовых характеристик и т.д. для принятия управленческих решений в условиях неопределенности.

Генеральная совокупность – это совокупность объектов, из которой производится выборка.

Выборочная совокупность (выборка) – это совокупность случайно отобранных объектов.

Если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n = 100.

При составлении выборки можно поступить двумя способами: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки делятся на повторные и бесповторные.

Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

На практике обычно пользуются бесповторным случайным отбором.

Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Выборка должна правильно представлять пропорции генеральной совокупности. Выборка должна быть репрезентативной (представительной).

В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществлять случайно.

Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается; в предельном случае, когда рассматривается бесконечная генеральная совокупность, а выборка имеет конечный объем, это различие исчезает.

В американском журнале «Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов относительно исхода предстоящих выборов президента США в 1936 году. Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве источника для генеральной совокупности исследуемых американцев были взяты справочники телефонных абонентов. Из них случайным образом были выбраны 4 миллиона адресов., по которым редакция журнала разослала открытки с просьбой высказать свое отношение к кандидатам на пост президента. Обработав результаты опроса, журнал опубликовал социологический прогноз о том, что на предстоящих выборах с большим перевесом победит Ландон. И … ошибся: победу одержал Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная часть населения, которые поддерживали взгляды Ландона.

На практике применяются различные способы отбора, которые можно разделить на 2 вида:

1. Отбор не требует расчленения генеральной совокупности на части (а) простой случайный бесповторный; б) простой случайный повторный).

2. Отбор, при котором генеральная совокупность разбивается на части. (а) типичный отбор; б) механический отбор; в) серийный отбор).

Простым случайным называют такой отбор, при котором объекты извлекаются по одному из всей генеральной совокупности (случайно).

Типичным называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типичной» части. Например, если деталь изготавливают на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных «типичных» частях генеральной совокупности.

Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой отбор может не обеспечивать репрезентативность выборки (если отбирают каждый 20-ый обтачиваемый валик, причем сразу же после отбора производится замена резца, то отобранными окажутся все валики, обточенные затупленными резцами).

Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергают сплошному обследованию. Например, если изделия изготавливаются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.

На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы.

4. Статистическое распределение выборки

Если количество вариант велико или выборка производится из непрерывной генеральной совокупности, то вариационный ряд составляется не по отдельным точечным значениям, а по интервалам значений генеральной совокупности. Такой вариационный ряд называется интервальным. Длины интервалов при этом должны быть равны.

Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.

Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (суммы частот, попавших в этот интервал значений)

Точечный вариационный ряд частот может быть представлен таблицей:

Источник

Элементы статистики

Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.

Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).

Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.

На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.

Выборка. Объем. Размах

Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней

Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6

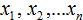
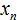
Элементы выборки обозначаются с помощью переменных с индексами . Последний элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.

Обозначим элементы нашей выборки через переменные

Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.

Размахом выборки называют разницу между самым большим и маленьким элементом выборки.

Среднее арифметическое

Понятие среднего значения часто используется в повседневной жизни.

Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.

Среднее арифметическое — это результат деления суммы элементов выборки на их количество.

Вернемся к нашему примеру

Узнаем сколько в среднем мы тратили в каждом из шести дней:

Средняя скорость движения

При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.

В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.

Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.

Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.

Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)

Значит автомобиль ехал со средней скоростью 71,08 км/ч.

Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:

Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:

Сложим эти расстояния и результат разделим на 5

Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:

Мода и медиана

Модой называют элемент, который встречается в выборке чаще других.

Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.

Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.

Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.

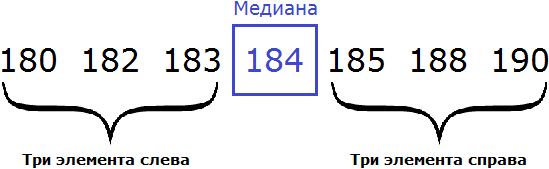
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

Выпишем рост спортсменов отдельно:

В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.

Медианой упорядоченной выборки называют элемент, располагающийся посередине.

Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.

В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану

Но возможны случаи, когда количество элементов выборки чётно.

К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 184, 186, 188, 190

В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.

В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.

Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186

Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.

Поэтому более точное определение медианы зависит от количества элементов в выборке.

Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.

Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.

Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190

Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:

Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:

0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1

Определим среднее арифметическое для данной выборки — получим значение 2,2

По данному значению можно сказать, что в среднем у спортсменов 2,2 очка

Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:

В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.

Частота

Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.

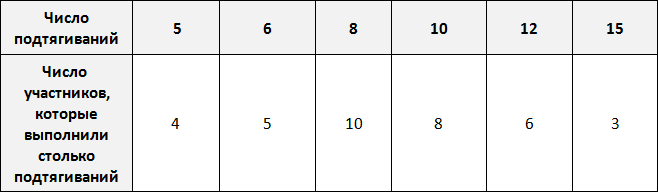
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.

По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.

Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.

Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.

Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:

4 + 5 + 10 + 8 + 6 + 3 = 36

Относительная частота

Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.

Относительная частота равна отношению частоты на общее число элементов выборки.

Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

42 thoughts on “Элементы статистики”

Спасибо, что вы вернулись.
Будут ли новые уроки?

Источник