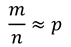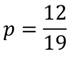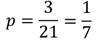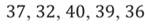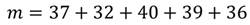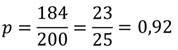Что такое частота случайного события
Что такое частота случайного события
§ 1. ОСНОВНЫЕ ПОНЯТИЯ
1.1. Случайные события. Частота. Вероятность.
Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий).
Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).
Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие.
Пусть при n испытаниях событие A появилось m раз.
Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n
Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Поясним это на примере.
Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты 12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5.
Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти.
Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.
Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.
Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 Дальше.
Относительная частота случайного события
Урок 30. Алгебра 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Относительная частота случайного события»
Примерами таких событий являются: выпадение орла или решки при подбрасывании монеты; поражение мишени или промах при стрельбе; выпадение того или иного количества очков при бросании игрального кубика.
Отношение частоты к общему числу испытаний называют относительной частотой этого события.
Пусть некоторое испытание проводилось многократно в одних и тех же условиях. При этом фиксировалось, произошло или нет некоторое интересующее нас событие А.
Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу всех испытаний.
В ходе исследований выяснилось, что относительная частота появления ожидаемого события при повторении опытов в одних и тех же условиях, может оставаться примерно одинаковой, незначительно отличаясь от некоторого числа р.
При подбрасывании монеты отмечают те случаи, когда выпадает орёл.
Если монета однородна и имеет правильную геометрическую форму, то шансы выпадения орла или решки будут примерно одинаковы. Но при небольшом количестве бросков такой результат может не получиться.
А вот если испытание проводиться большое количество раз, то относительная частота выпадения орла близка к относительной частоте выпадения решки.
Многие учёные проводили такой эксперимент.
Так, например, английский математик Карл Пирсон бросал монету 24 тысячи раз, и относительная частота выпадения орла оказалось равной 0,5005.
А наш соотечественник, Всеволод Иванович Романовский, подбрасывая монету 80 тысяч 640 раз, нашёл, что относительная частота выпадения орла в его испытании была равна 0,4923.
Заметим, что в обоих случаях относительная частота выпадения орла очень близка к 
.
Говорят, что вероятность выпадения орла при подбрасывании монеты правильной геометрической формы равна .
В непрозрачном мешке лежит 7 зелёных и 12 синих кубиков. За раз можно доставать только 1 из них. Какова вероятность того, что из мешка достанут синий кубик?
Всего в мешке 19 кубиков. Значит, n=19.
Синий кубик мы можем достать 12 раз. Получаем, что m=12.
Относительная частота равна:
Вероятность того, что из мешка достанут синий кубик, равна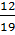 
.
Определить относительную частоту появления буквы «о» в слове «достопримечательность».
Общее число букв, то есть n=21. А количество букв «о», то есть m=3.
Значит относительная частота:
Отмечая число попаданий в корзину в каждой серии из 40 бросков, которые совершал баскетболист, получили такие данные:
Какова относительная вероятность попадания мяча в корзину для данного баскетболиста?
Определим общее число бросков. Было 5 серий по 40 бросков, то есть n=200.
Сосчитаем число попаданий в корзину:
Относительная вероятность попадания в корзину будет:
Стрелок совершил 50 выстрелов. Относительная частота попадания в цель оказалась равной 0,88. Сколько раз он промахнулся?
Зная общее число выстрелов n=50 и относительную вероятность попадания p=0,88. Найдем число попаданий в цель:
Алгебра
План урока:
Частота и вероятность
В мире происходят события, которые можно предсказать. Например, можно предсказать приезд лифта после того, как человек нажмет кнопку его вызова. Астрономы могут заранее предсказывать солнечные и лунные затмения.
Однако нередко нам приходится иметь дело с событиями, результат которых заранее предсказать невозможно. Не получается заранее сказать, упадет ли монетка при подбрасывании орлом вверх, также как нельзя заранее предсказать поломку прибора. Такие события называются случайными.
Случайные события обычно могут произойти только в определенной ситуации. Так, событие «выпадение решки» может произойти только при броске монеты. В математике подбрасывание монетки будет называться испытанием или экспериментом.
Здесь не следует воспринимать термин «эксперимент» как некое научное исследование. Испытанием может оказаться любая жизненная ситуация. Приведем несколько примеров опытов и соответствующих им случайных событий:
Здесь важно отметить, что для математики не важно, является ли событие по-настоящему случайным. Возможно, что автобус ходит строго по расписанию, и человек, знающий его, точно может определить, через сколько минут он приедет. Но если рядом стоит другой человек, не знающий этой информации, то для него приезд автобуса будет случайным событием.
Предположим, что есть возможность провести какой-то эксперимент множество раз. Например, кубик можно бросить 500 раз. Обозначим это число, количество экспериментов, как n. В ходе серии этих бросков шестерка выпала, например, 85 раз. Обозначим эту величину, количество произошедших случайных событий, как m. Само событие «выпадение шестерки» обозначим как А. Тогда отношение m/n будет называться частотой случайного события А. В данном случае частота события А равна
Наблюдения показывают, что если условия экспериментов примерно одинаковы, а их число велико, то частота одного и того же события будет примерно одинаковой. Чем больше число испытаний, тем обычно ближе частота события к некоторому постоянному числу. Это число и называют вероятностью случайного события А.
Грубо говоря, частота и вероятность событий – это примерно одно и то же. Частоту определяют на практике, входе эксперимента, а вероятность можно рассчитать аналитически.
Вероятность – это величина, которая характеризует возможность события произойти. Если она близка к единице, то событие, скорее всего, произойдет. Если она близка к нулю, то событие, скорее всего, не случится. Для обозначения вероятности используется буква Р. Если надо указать вероятность конкретного события А, то его записывают как Р(А).
Вероятность – это безразмерная величина, то есть для нее нет никакой единицы измерения. Она может принимать значение от 0 до 1. Иногда на практике ее указывают в процентах. Например, вероятность 0,5 означает 50%. Чтобы перевести вероятность в проценты, ее надо просто умножить на 100.
Элементарные события
Часто одно случайное событие можно представить как результат нескольких случайных событий. Например, событие «выпадение на кубике четного числа» произойдет в том случае, если случится хотя бы одно из следующих событий:
Если событие нельзя «разбить» на более простые события, то его называют элементарным событием. Считается, что в ходе испытания может произойти только одно элементарное событие. Так, при броске кубика произойдет одно из 6 элементарных событий:
В большинстве случаев вероятность элементарных событий одинакова. Действительно, нет причин полагать, что при броске кубика шестерка будет выпадать чаще двойки. Если у двух элементарных событий одинаковая вероятность, то их называют равновозможными событиями.
Если в результате эксперимента происходит одно из равновозможных событий, число которых равно n, то вероятность каждого из них принимается равной дроби 1/n.
Например, при броске кубика может произойти 6 равновозможных событий. Значит, вероятность каждого из них равна 1/6. При броске монетки она может выпасть либо орел, либо решка. Этих событий два, и они равновозможны, поэтому их вероятность равна 1/2, то есть 0,5.
Пример. В урне 20 шариков, один из которых окрашен в желтый цвет. Какова вероятность, что человек, вытаскивающий вслепую один из шариков, вынет именно желтый шар?
Решение. Так как шаров 20, то возможны 20 равновозможных событий, одно из которых – вытаскивание желтого шара. Его вероятность равна 1/20 = 0,05
Пример. Вася составил произвольную последовательность из букв А, Б, В, Г, Д, и записал ее на бумаге. Каждую букву Вася использовал один раз. Аналогично свою последовательность записал и Петя. Какова вероятность, что они оба загадали одну и ту же последовательность.
Решение. Вася записал перестановку 5 букв. Общее количество таких перестановок равно 5! = 1•2•3•4•5 = 120. Все последовательности равновероятны. Значит, вероятность того, что они совпали, равна 1/120.
Противоположные события
Заметим, что если сложить вероятности всех элементарных событий, которые возможны в ходе эксперимента, то получится единица. Действительно, при броске монеты возможны два события с вероятностью 1/2. Сумма их вероятностей составляет 1/2 + 1/2 = 1.
Это правило действует и в том случае, когда речь идет о не равновозможных событиях. Так, при выстреле по мишени возможны два варианта развития событий – попадание в цель или промах. Пусть вероятность попадания в цель равна 0,3. Это значит, что вероятность промаха составляет 0,7, так как только в этом случае сумма этих вероятностей будет равна единице:
Заметим, что при стрельбе стрелок либо попадет в цель, либо промажет. То есть одно из двух этих событий обязательно произойдет, но только оно одно. Подобные события называют противоположными.
Противоположными являются такие события, как:
Стоит отметить, что победа одной и победа другой команды в футбольном матче – это не противоположные события, так как возможен третий исход – ничья. Однако в ряде спортивных состязаний ничья невозможна, и тогда победы команд – это противоположные события.
Очевидно, что сумма вероятностей противоположных событий равна единице.
Пример. Вероятность того, что рабочий изготовит годную деталь, оценивается в 0,97. Чему равна вероятность изготовления бракованной детали?
Решение. Изготовление бракованной детали (обозначим это событие как А) и получение годного изделие (событие Б) – это два противоположных события. Их сумма равна единице
По условию Р(А) = 0,97. Тогда
Перенесем в равенстве слагаемое 0,97 в правую часть и получим:
Сложение вероятностей
До этого мы рассматривали элементарные события. Однако значительно чаще нас интересуют более сложные события, которые состоят из элементарных. Как рассчитать их вероятность?
Введем понятие несовместных событий.
Так, при броске кубика не может сразу выпасть пятерка и четное число (потому что 5 – это нечетное число). Хоккейный матч не может одновременно окончиться и ничьей, и победой одной из команд.
Заметим, что любые два элементарных события несовместны, также как и любые два противоположных события.
Для несовместных событий справедлива теорема сложения вероятностей.
Пример. В забеге на 1500 метров участвуют два китайца. Эксперты полагают, что вероятность победы Мао Луня составляет 0,16, а шансы Ван Юнпо оцениваются в 0,14. Если эти оценки справедливы, то каковы шансы того, что чемпионом станет китаец?
Решение. Обозначим победу Мао Луня как событие А, а победу Ван Юнпо – как Б. Очевидно, что события несовместны, так как победитель будет лишь один. По Условию Р(А) = 0,16, а Р(В) = 0,14.
Событие «победа китайца» произойдет, если выиграет хоть один из этих спортсменов, поэтому произведем сложение вероятностей:
Р(А или В) = Р(А) + Р(В) = 0,16 + 0,14 = 0,3
Заметим, что выполнять сложение вероятностей событий можно и в случае, когда несовместных событий больше двух.
Пример. При стрельбе по мишени стрелок выбьет 10 баллов (максимальный результат) с вероятностью 0,2, 9 баллов с вероятностью 0,25, 8 баллов с вероятностью 0,15. Какова вероятность, что стрелок НЕ наберет даже 8 баллов одним выстрелом?
Решение. Здесь несовместные события – это выбивание 10 (событие А), 9 (В) и 8 (С) баллов. Действительно, в ходе одного выстрела стрелок покажет только один результат. Если одно из этих событий случится, то спортсмен получит не менее 8 баллов. Вероятность этого события равна:
Р(А или В или С) = 0,2 + 0,25 + 0,15 = 0,6
Но нас спрашивают о другом, о вероятности того, что стрелок НЕ наберет 8 очков. Очевидно, что он их либо наберет, либо нет. Значит, это противоположные события, поэтому сумма равняется 1. Мы посчитали, что стрелок наберет 8 баллов с вероятностью 0,6. Значит, он не наберет их с вероятностью
Пример. В урне лежит 500 шариков, из которых 120 являются черными. Человек вслепую вытаскивает из урны один шар. Какова вероятность, что он будет черным.
Решение. Присвоим каждому шару номер от 1 до 500, причем первые 120 номеров получат черные шары. Обозначим вероятность того, что вытащат шар с номером n, как Р(n). Очевидно, что события «выбран шар 1», «выбран шар 2», … «выбран шар 500» – это элементарные и равновозможные события. Их вероятность равна 1/500:
Р(1) = Р(2) = Р(3) =…..=Р(500) = 1/500
Эти события несовместны, как и любые элементарные события. Значит, вероятность того, что вытащат черный шар, равна сумме вероятностей:
Р(выбран черный шар) = Р(1) + Р(2) + … + Р(120)
В этой сумме 120 слагаемых, каждое из которых равно 1/500. Следовательно, вся сумма равна произведению 120 и 500
Р(выбран черный шар) = 120•(1/500) = 120/500 = 0,24
В этом примере рассматривался особый случай, когда все элементарные события (вытаскивание конкретного шарика) равновозможны, и несколько из них приводили к одному событию (вытаскиванию черного шара). В итоге мы получили, что вероятность этого события равна отношению числа «благоприятных» для него равновозможных событий (120) к общему числу этих событий (500). Такой же результат мы получим при рассмотрении любой схожей задачи.
В результате мы получили одну из основных формул теории вероятности.
Пример. Компьютер случайным образом генерирует число от 1 до 200. Вероятность появления каждого числа одинакова. Какова вероятность того, что он сгенерирует число от 51 до 75 (включительно)?
Решение. Задача предполагает 200 равновозможных исходов события. Из них 25 (между 51 и 75 находится 25 чисел) являются «благоприятными». Тогда вероятность описанного события равна отношению 25 к 200:
Р = 25/200 = 1/8 = 0,125
Ещё раз напомним принципиальный момент. Такой метод решения задач может быть применен только в том случае, когда все элементарные события равновероятны!
Пример. Изготовлено 10 велосипедов, но из них 3 – с дефектом. Необходимо выбрать 4 велосипеда. Каков шанс, что они все будут без дефекта?
Решение. Выбирая 4 велосипеда из 10, мы составляем, с точки зрения комбинаторики сочетание из 10 по 4. Подсчитаем количество возможных сочетаний:
Теперь подсчитаем, сколько можно составить сочетаний, не содержащих дефектный велосипед. Годных велосипедов 10 – 3 = 7, из них надо выбрать 4. Имеем сочетания из 7 по 4:
Вероятность выбора качественных велосипедов равна отношению количества «благоприятных» исходов (их 35) к общему числу возможных исходов:
Пример. В турнире по футболу участвуют команды «Барселона», «Реал», «Атлетико» и «Валенсия». Эксперты полагают, что:
Определите вероятность победы каждой команды в турнире.
Обозначим за х вероятность победы «Валенсии». Шансы «Реала» и «Атлетико» в 1,5 раза выше, а потому составляют по 1,5х. Вероятность триумфа «Барселоны» в 4 раза выше, чем у «Реала», а потому составляют 4•1,5х = 6х.
Ясно, что турнир выиграет лишь одна команда, то есть речь идет о несовместных событиях. С другой стороны, какая-то команда обязательно его выиграет, а потому в вероятности побед команд дадут единицу. В результате, используя формулу сложения вероятностей, можно записать уравнение:
х + 1,5х + 1,5х + 6х = 1
Решив уравнение, мы нашли, что шансы триумфа «Валенсии» составляют всего 0,1. Шансы «Реала» и «Атлетико» равны
Вероятность успеха «Барселоны» составляет
Ответ. «Барселона» – 0,6, «Реал» и «Атлетико» – по 0,15, «Валенсия» – 0,1.
Умножение вероятностей
До этого мы рассматривали сложные события, которые происходили тогда, когда происходило одно из элементарных событий. Например, в забеге, где участвовали два китайца, представитель Поднебесной побеждал, если выигрывал ИЛИ 1-ый китаец, ИЛИ 2-ой. Ключевое слово здесь – ИЛИ.
Однако в некоторых случаях событие происходит лишь тогда, когда происходят одновременно сразу два более простых события. Пусть надо вычислить вероятность того, что при двух подбрасываниях монеты они оба раза упадет на орлом вверх. Возможны 4 случая:
Все 4 исхода удобно представить в виде таблицы. По вертикали запишем результат 1-ого броска монеты, а по горизонтали – второго:
Видно, что лишь в одном из 4 случаев орел выпадет оба раза. Поэтому вероятность будет равна 1/4, или 0,25.
Этот результат можно было получить иначе. Событие ОО случится, только если случатся два события: Орел выпадет при первом броске,и он же выпадет во второй раз. Вероятность каждого из них равна 1/2, или 0,5. Если перемножить эти две вероятности, то снова получим 0,5•0,5.
Рассмотрим более сложный случай с броском двух шестигранных кубиков. Какова вероятность, что в сумме выпадет ровно 12 очков. Снова построим таблицу, по вертикали укажем результат первого броска, по горизонтали – второго, а в ячейках – выпавшую сумму:
Всего получилась табличка с 36 ячейками. Лишь в одной из них стоит число 12. Эта сумма на кубиках будет лишь тогда, когда на обоих кубиках выпадет по шестерке. Так как ячеек 36, а каждая комбинация равновозможна, то вероятность выпадения 12 равна 1/36. Обратите особое внимание, что, например, семерка записана сразу в 6 ячейках (по диагонали, начиная с нижнего левого угла). Значит, вероятность выпадения семерки за 2 броска равна 6/36 = 1/6. И действительно, на практике 7 очков выпадет у игроков в 6 раз чаще, чем 12. Посчитайте с помощью таблицы самостоятельно, какого вероятность выпадения 10 очков.
Как и в случае с монеткой, число вероятность 1/36 можно получив, перемножив вероятность того, что в первой кости выпадет шестерка (1/6), и того, что на второй кости выпадет она же (1/6):
Введем одно важное понятие – независимые события.
Так, какое бы число не выпало на 1-ой кости, вероятность выпадения на второй, например, четверки останется равной 1/6. Как бы ни падала монетка при первом броске, при 2-ом шанс выпадения орла останется равным 1/2.
Для наглядности приведем пример зависимых событий. Пусть А – вероятность победы в забеге одного бегуна, и Р(А) = 0,1. В – вероятность победы второго бегуна, и Р(В) = 0,1. Но очевидно, что победить может лишь один спортсмен. Поэтому, если случится событие А, то вероятность события В изменится – она опустится до нуля.
Таблички, которые мы строили для игры в кости, не всегда удобно использовать, поэтому на практике используют теорему умножения вероятностей.
Ещё раз обратим внимание, что оно действует только для независимых случайных событий.
Пример. Рабочий изготавливает две детали. Вероятность изготовления первой детали с браком составляет 0,05, а второй детали – 0,02. Рабочего оштрафуют, если обе детали будут сделаны с браком. Какова вероятность штрафа для рабочего?
Решение. Штраф выпишут, если одновременно произойдет два независимых события – будет допущен брак при изготовлении И 1-ой, И 2-ой детали. Ключевое слово – И, а не ИЛИ, как в случае со сложением вероятностей. Вероятность такого развития событий найдем, произведя умножение вероятностей:
Умножение вероятностей событий возможно и тогда, когда их больше двух.
Пример. Для победы команды в турнире ей надо выиграть все 4 оставшиеся встречи. Вероятность победы в каждой игре составляет 80%. Какова вероятность победы в турнире?
Решение. Обозначим вероятности победы в отдельных матчах как Р1, Р2, Р3, Р4. По условию они все равны 0,8. Команда станет чемпионом, только если случатся все события. Вероятность этого можно найти, применив формулу умножения вероятностей:
Пример. В первой партии 4% лампочек бракованы, а во второй – 5%. Из каждой партии берут по лампочке. Какова вероятность того, что обе выбранных лампочки окажутся бракованными? Какова вероятность, что они обе окажутся исправными? Какова вероятность, что ровно одна лампа будет бракованной?
Решение. Обозначим выбор бракованной детали из 1-ой партии как событие «брак-1», а выбор годной детали (годная-1). Эти события противоположны, то есть сумма их вероятностей равна единице.
Р(брак-1) + Р(годная-1) = 1
Р(годная-1) = 1 – Р(брак-1)
По условию Р(брак-1) = 0,04. Следовательно, Р(годная-1) = 1 – 0,04 = 0,96.
Аналогично для второй партии можно записать, что Р(брак-2) = 0,05, Р(годная-2) = 0,95.
Будут выбраны две бракованные детали только в том случае, когда произойдут события Р(брак-1) и Р(брак-2). Вероятность этого, по правилу умножения вероятностей, равна:
Две годные детали бут выбраны, если одновременно случатся события Р(годная-1) и Р(годная-2). Это случится с вероятностью
Пример. По мишени стреляют из двух орудий. Вероятность попадания из первого орудия составляет 0,3, а из второго – 0,4. С какой вероятностью по мишени попадет ровно одно орудие?
Решение. Пусть событие «попал-1» означает попадание из 1-ого орудия, а «попал-2» – попадание из 2-ого орудия. Казалось бы, нам надо найти вероятность попадания ИЛИ 1-ого, ИЛИ 2-ого орудия. Однако слово ИЛИ здесь не означает, что вероятности можно просто сложить! Вспомним, что закон сложения вероятностей действует только для несовместных событий. Но выстрелы из орудий таковыми не являются, так как возможно одновременное попадание двух снарядов в мишень.
Введем события «промах-1» и «промах-2», означающие промах из 1-ого или второго орудия. Их вероятности составляют
Р(«промах-1») = 1 – Р(«попал-1») = 1 – 0,3 = 0,7
Р(«промах-2») = 1 – Р(«попал-2») = 1 – 0,4 = 0,6
Одно попадание случится в случае, если произойдет одно из двух «сложных» событий:
Вероятность события А можно рассчитать так:
Р(А) = Р(«попал-1») •Р(«промах-2») = 0,3•0,6 = 0,18
Аналогично рассчитаем и вероятность Б:
Р(Б) = Р(«попал-2») •Р(«промах-1») = 0,4•0,7 = 0,28
События А и Б несовместны, а потому их вероятности можно сложить
Р(А) + Р(Б) = 0,18 + 0,28 = 0,46
Условная вероятность
Иногда можно перемножать вероятности событий, не являющихся в полном смысле слова независимыми. Пусть для того, чтобы произошло событие А, необходимо, чтобы последовательно произошли В и С. В зависимости от того, произошло ли В, вероятность С может отличаться. Например, в урне лежат 4 шарика – 2 красных и 2 желтых. Предположим, что произошло событие В – был вытащен красный шар. Его вероятность равна 0,5. Чему тогда равна вероятность события С – вытаскивания желтого шарика? В урне осталось 3 шара, из них 2 желтых, поэтому Р(С) = 2/3.
С другой стороны, пусть В не произошло, то есть первым был вынут желтый шар. Чему тогда равна вероятность С? В урне снова 3 шарика, но лишь 1 из них желтый. Следовательно, Р(С) = 1/3. Получается, что в зависимости от того, случилось ли В, вероятность Р(С) принимает разные значения. В математике такую вероятность называют условной.
Обозначается она так:
Первая буква в скобках соответствует событию, для которого указываем вероятность, а вторая буква – событию, которое является условием для С.
Если событие А произойдет тогда, когда свершится сначала В, а потом С, то вероятность А также можно найти с помощью умножения
Пример. В урне находится 52 шара, из них на 4 написана буква Т. Из урны последовательно вынимаются два шара. Какова вероятность, что на обоих вытащенных шарах будет буква Т?
Решение. Так как в урне 52 шара, и лишь на 4 есть буква Т, то шанс на то, что первым вытащат именно шар с буквой Т, равен 4/52 = 1/13. Если это событие произошло, то в урне остался 51 шар, и лишь на трех будет находиться нужный символ. Тогда вероятность появления шара с буквой Т составит 3/51 = 1/17. Общая же вероятность появления 2 таких шаров подряд найдется как произведение этих вероятностей:
Р = (1/13)•(1/17) = 1/221 ≈ 0,004525
Эту вероятность можно рассчитать и иначе, по аналогии с задачей про бракованные велосипеды, которая приведена выше. Подсчитаем, сколькими способами можно выбрать 2 шара из 52:
Но всего 6 способами можно выбрать 2 шара из 4:
Поделив число благоприятных исходов на их общее количество, получим искомую вероятность:
Пример. Известно, что вероятность мужчины дожить до 90 лет составляет 5,126%, а до 95 лет – 1,326%. С какой вероятностью мужчина, которому уже сейчас 90 лет, доживет до 95 лет?
Решение. Пусть А – это дожитие до 95 лет, С – дожитие 90-летнего мужчины до 95 лет, В – дожитие до 90 лет. Чтобы отпраздновать 95-летие, человек сначала должен отметить 90-летний юбилей, а потом ещё прожить 5 лет. Другими словами, чтобы случилось А, сначала должно случиться В, а потом событие С при условии В. То есть можно записать
По условию Р(А) = 0,01326, а Р(В) = 0,05126. Зная это, легко найдем Р(С|B):
Р(С|B) = 0,01326/0,05126 ≈ 0,2587
Это и есть вероятность мужчины, отметившего 90-ый день рождения, дожить до 95 лет.
Вероятность и геометрия
Теория вероятности затрагивает и геометрию. Пусть есть отрезок АВ, в середине которого располагается точка С.
Теперь мы ставим на отрезке АВ случайную точку D. С какой вероятностью она попадет наАС, а с какой на ВС? Так как эти отрезки ничем не отличаются, то можно предположить, что события «попадание точки на АС» и «попадание точки на ВС» являются равновероятными событиями. Так и есть. Их вероятность обоих событий составляет 0,5.
Теперь предположим, что точка С выбрана так, что отрезок АС вдвое короче, чем ВС, то есть ВС = 2 АС:
Чему в этом случае равны вероятности попадания случайной точки D на отрезки АС и ВС? Для ответа на этот вопрос раздели ВС надвое с помощью ещё одной точки K:
Получили три одинаковых отрезка АС, СК и КВ. Раз они одинаковы, то и вероятности случайной точки оказаться на каждом из этих отрезков равны:
Отсюда вероятность попадания точки на ВС равна 2/3:
Р(ВС) = Р(СК) + Р(КВ) = 1/3 + 1/3 =2/3
Получили, что вероятность попадания точки на ВС вдвое выше, чем на АС. И при этом ВС вдвое длиннее. И это не случайно. В общем случае верно следующее правило:
Данное свойство может пригодиться не только в геометрии, но и при решении задач.
Пример. Прохожий пришел на остановку автобуса в случайный момент времени. Он знает, что автобус ходит с интервалом в 40 минут, но не знает, когда отъехал предыдущий автобус. С какой вероятностью автобус придется ждать менее 10 минут?
Решение. Построим схему. На ней время будем откладывать по горизонтальной оси. Отметим точки, соответствующие приезду автобуса (А1, А2, А3, А4), и точку, соответствующую приходу прохожего (D):
Ясно, что точка D окажется между какими-то двумя точками, которым соответствуют последовательные прибытия поезда.На рисунке это А2 и А3. В каком случае время ожидания составить менее 10 минут? В том случае, если точка D окажется на «расстоянии» менее 10 минут от точки А3, то есть попадет в отрезок ВА3:
Отрезок ВА3 вчетверо короче отрезка А2А3, поэтому вероятность точку D попасть на него составляет 1/4. Именно такова вероятность, что прохожему придется ждать автобус менее 10 минут.
В случае, когда точка случайным образом ставится не на отрезке, а на плоской фигуре, то справедливо следующее правило:
Пример. В треугольнике АВС проведена средняя линия NM. С какой вероятностью случайная точка, отмеченная на треугольнике АВС, попадет и на треугольник ANM?