Окружность с чего начать
Как построить окружность?
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а) 2 + (у – b) 2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
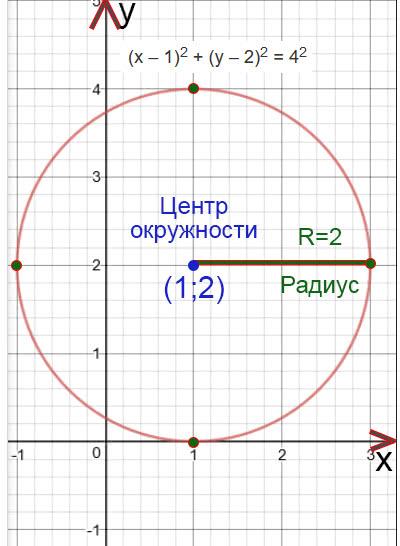
Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2
Найдем центр окружности:
х – 1=0
x=1
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.
Пример №2:
х 2 + (у + 1) 2 =1
Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2
Найдем центр окружности:
х=0
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1
Построим окружность.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Окружность с чего начать
циркуль.
если начинать с листа бумаги,то в таком случае вопрос должен звучать иначе-
«На столе лежат линейка, карандаш, циркуль и резинка. (На листе бумаги-этого не надо упоминать)нужно начертить окружность. С чего начать?
в таком случае,не упоминая,то надо начинать с листа,а в твоём условии,то только с циркуля.
странное у людей мышление.
так ведь из задания ясно-на листе,значит и брать его не надо.
есть лист,чего его брать.
юмористы.
постараюсь тоже быть предвзятым..;) ))))
—
надо начать с наезда на лаборанта, который позаботился обо всём, кроме необходимого формата «бумаги». ))) (так лист или бумага.? )))), упаковочная, или туалетная, или ещё какая. ))
потом наехать на преподавателя, которая дала неполную информацию о задании, не указав радиус или диаметр окружности, и прочие нюансы..))))), и т.д. ))
Сначала надо обмакнуть Антона в медузу,после чего просидев пятнадцать суток срочно превратить Олю Бузову в Эль Мундо и превратившись в сметану прыгнуть в средину множества зябликов.После чего взять лист бумаги начать чертить Аргентину и пьяную женщину Авдотью Михайловну. O_o
Всё про окружность и круг
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Окружность. Круг. Приемы работы циркулем, использование трафаретов
Цели и задачи:
Тип урока: комбинированный.
Формы работы: индивидуальная, групповая.
Ход занятия:
Организационный момент:
Проверка готовности к уроку.
Повторение:
Анализ графического упражнения.
Новый материал:
Рубрика «Это интересно!»
С незапамятных времен человек использовал в своей жизни простейшие геометрические построения. Одним из таких построений является деление окружности на равные части. Примеров можно привести много. Превращение колеса из сплошного диска в обод со спицами поставило человека перед необходимостью распределить спицы в колесе равномерно.
С делением окружности неразрывно связано построение правильных многоугольников. Правильные многоугольники встречаются в древнейших орнаментах у всех народов.
В декоративно- прикладном искусстве дизайнеры, ювелиры и представители многих других профессий с успехом применяли деление окружности, создавая прекрасные произведения. Это ордена, медали, монеты и ювелирные украшения.

Орден Красной Звезды
Орден Отечественной войны
Самым распространенным примером применение деления окружности на равные части является создание логотипов, эмблем, товарных знаков различных фирм. Иногда достаточно увидеть эмблему на капоте или крыле автомобиля и безошибочно назвать марку.
Показ наглядных пособий использования геометрических построений в строительстве, архитектуре, машиностроении, а также природные явления.
Построение круга, окружности.
Круг – это часть плоскости, ограниченная окружностью.
Окружность – замкнутая плоская кривая, все точки которой равноудалены от центра.
Чтобы изобразить круг, достаточно взять блюдце или тарелку и обвести.
Для построения окружности необходимо найти центр. Из центра циркулем провести окружность.
Этапы построения:
Запомнить: в центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки. В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.
Для построения окружностей и кругов используют трафареты.
Демонстрация, показ.
Деление окружности на равные части.
Любая прямая, проведенная через центр окружности, делит эту окружность на две равные части. Две взаимно перпендикулярные прямые, проведенные через центр окружности, делят эту окружность на 4 равные части.
Окружность можно разделить на 8 равных частей, используя линейку или угольники.
Демонстрация, показ.
Если соединить, полученные при делении точки окружности, то мы получим правильные многоугольники.
При делении окружности на 3, 6, 12 равных частей используют не только угольники, но и циркуль. В результате построения можно увидеть правильный равносторонний треугольник, правильный шестиугольник (рисунок 5)
Демонстрация, показ.
Физкультурная пауза.
Закрепление:
Фрагмент из рабочей тетради.
Приготовь для работы циркуль, карандаш с маркировкой Т и ТМ, линейку, трафарет. Все построения выполняй аккуратно.
Используя трафарет с окружностями, изобрази круг.
Для построения окружности необходимо провести штрихпунктирные линии. Эти линии состоят из штриха и точки. При пересечении они образуют центр окружности и являются центровыми или осевыми линиями.
Установи ножку циркуля в центре пересечения осевых (центровых) линий и проведи окружность.
Этапы построения окружности:
Центр окружности является также и центром круга.
Запомни:
В центре должны обязательно пересекаться штрихи, проведенных центровых (осевых) линий, а не точки.
В окружностях меньших размеров допускается проводить вместо штрихпунктирных линий тонкие линии построения.
Рубрика «ЗАПОМНИ»: круг, окружность, осевая линия, центровая линия, штрихпкнктирная линия.
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Теорема 4:
Равные хорды стягивают равные дуги.
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.