Односвязный список что это
Реализация односвязного списка на c++
Эта картинка демонстрирует, как будет выглядеть односвязный список.
Реализация узла
Значение, которое будет задавать пользователь
Указатель на следующий элемент (по умолчанию nullptr)
Реализация односвязного списка
Указатель на первый узел
Указатель на последний узел
Функция проверки наличия узлов в списке
Функция добавления элемента в конец списка
Функция печати всего списка
Функция поиска узла в списке по заданному значению
Функция удаления первого узла
Функция удаления последнего узла
Функция удаления узла по заданному значению значению
Функция обращения к узлу по индексу (дополнительная функция)
Реализация 1-3 пункта
Функция проверки наличия узлов в списке
Функция добавления элемента в конец списка
Здесь надо рассмотреть два случая:
В обоих случаях надо создать сам узел со значением, которое мы передали в эту функцию.
Первый случай:
Здесь нам как раз пригодиться функция проверки наличия узлов. Если список пустой, тогда мы присваиваем указателю на первый узел и последний узел указатель на новый узел и выходим из функции.
Второй случай:
Нам уже не нужно проверка наличия узлов в списке, так как если первый случай не происходит, то в списке есть узлы. Раз мы добавляем в конец, надо указать, что новый узел стоит после последнего узла. Затем мы меняем значения указателя last.
Теперь в список можно добавлять элементы.
Функция печати всего списка
Тест уже написанных функций
Код который мы написали:
Функция поиска узла в списке по заданному значению
Также делаем проверку is_empty() и создаём указатель p на первый узел
Обходим список, пока указатель p не пустой и пока значение узла p не равно заданному значению. После цикла возвращаем наш узел
Функция удаления первого узла
Функция удаления последнего узла
Конец списка одновременно и начало
Когда размер списка больше одного
Первый случай:
Сравниваем указатель на первый узел и указатель на последний узел, если они равны, то вызываем функцию удаления первого узла.
Второй случай:
Функция удаления узла по заданному значению значению
Делаем проверку is_empty(). И рассматриваем уже три случая:
Узел, который нам нужен, равен первому
Узел, который нам нужен, равен последнему
Когда не первый и не второй случаи
Первый случай:
Сравниваем значение первого узла с заданным значением, если значения совпадают, тогда вызываем функцию удаления первого узла.
Второй случай:
Сравниваем значение последнего узла с заданным значением, если значения совпадают, тогда вызываем функцию удаления последнего узла.
Третий случай:
Функция обращения к узлу по индексу
Для этой функции надо перегрузить оператор []
Тест программы
Заключение
Вот Вы и научились реализовывать односвязный список, и, надеюсь, стали лучше его понимать.
Односвязный список
Введение. Основные операции
О дносвязный список – структура данных, в которой каждый элемент (узел) хранит информацию, а также ссылку на следующий элемент. Последний элемент списка ссылается на NULL.
Для нас односвязный список полезен тем, что
Для простоты рассмотрим односвязный список, который хранит целочисленное значение.
Односвязный список состоит из узлов. Каждый узел содержит значение и указатель на следующий узел, поэтому представим его в качестве структуры
Чтобы не писать каждый раз struct мы определили новый тип.
Теперь наша задача написать функцию, которая бы собирала список из значений, которые мы ей передаём. Стандартное имя функции – push, она должна получать в качестве аргумента значение, которое вставит в список. Новое значение будет вставляться в начало списка. Каждый новый элемент списка мы должны создавать на куче. Следовательно, нам будет удобно иметь один указатель на первый элемент списка.
Вначале списка нет и указатель ссылается на NULL.
Для добавления нового узла необходимо
1) Создаём новый узел
2) Присваиваем ему значение
3) Присваиваем указателю tmp адрес предыдущего узла
4) Присваиваем указателю head адрес нового узла
5) После выхода из функции переменная tmp будет уничтожена. Получим список, в который будет вставлен новый элемент.
Так как указатель head изменяется, то необходимо передавать указатель на указатель.
Теперь напишем функцию pop: она удаляет элемент, на который указывает head и возвращает его значение.
Если мы перекинем указатель head на следующий элемент, то мы потеряем адрес первого и не сможем его удалить и тем более вернуть его значения. Для этого необходимо сначала создать локальную переменную, которая будет хранить адрес первого элемента
Уже после этого можно удалить первый элемент и вернуть его значение
Не забываем, что необходимо проверить на NULL голову.
Для дальнейшего разговора необходимо реализовать функции getLast, которая возвращает указатель на последний элемент списка, и nth, которая возвращает указатель на n-й элемент списка.
Так как мы знаем адрес только первого элемента, то единственным способом добраться до n-го будет последовательный перебор всех элементов списка. Для того, чтобы получить следующий элемент, нужно перейти к нему через указатель next текущего узла
Переходя на следующий элемент не забываем проверять, существует ли он. Вполне возможно, что был указан номер, который больше размера списка. Функция вернёт в таком случае NULL. Сложность операции O(n), и это одна из проблем односвязного списка.
Для нахождение последнего элемента будем передирать друг за другом элементы до тех пор, пока указатель next одного из элементов не станет равным NULL
Для вставки нового элемента в конец сначала получаем указатель на последний элемент, затем создаём новый элемент, присваиваем ему значение и перекидываем указатель next старого элемента на новый
Односвязный список хранит адрес только следующего элемента. Если мы хотим удалить последний элемент, то необходимо изменить указатель next предпоследнего элемента. Для этого нам понадобится функция getLastButOne, возвращающая указатель на предпоследний элемент.
Функция должна работать и тогда, когда список состоит всего из одного элемента. Вот теперь есть возможность удалить последний элемент.
Удаление последнего элемента и вставка в конец имеют сложность O(n).
Можно написать алгоритм проще. Будем использовать два указателя. Один – текущий узел, второй – предыдущий. Тогда можно обойтись без вызова функции getLastButOne:
Теперь напишем функцию insert, которая вставляет на n-е место новое значение. Для вставки, сначала нужно будет пройти до нужного узла, потом создать новый элемент и поменять указатели. Если мы вставляем в конец, то указатель next нового узла будет указывать на NULL, иначе на следующий элемент
Покажем на рисунке последовательность действий
После этого делаем так, чтобы новый элемент ссылался на следующий после n-го
Односвязный список
Каждый элемент списка мы представим программно с помощью структуры, которая состоит из двух составляющих:
1.Одно или несколько полей, в которых будет содержаться основная информация, предназначенная для хранения.
2. Поле, содержащее указатель на следующий элемент списка.
Отдельные объекты подобной структуры мы далее будем называть узлами, связывая их между собой с помощью полей, содержащих указатели на следующий элемент.
После создания структуры, нам необходимо инкапсулировать её объекты в некий класс, что позволит управлять списком, как цельной конструкцией. В классе будет содержаться два указателя (на хвост, или начало списка и голову, или конец списка), а так же набор функции для работы со списком.
В целом, полученный список можно представить так:
Итак, основные моменты создания списка, мы рассмотрели, переходим непосредственно к его формированию.
Формирование списка. Отведем место для указателей в статической памяти.
Зарезервируем место для динамического объекта.
Присвоим значение переменной ptail, и поместим в информационное поле значение элемента.
Переменная ptail должна содержать адрес последнего добавленного элемента, т. к. он добавлен в конец.
Если требуется завершить построение списка, то в поле указателя последнего элемента нужно поместить NULL.
В результате построен линейный односвязный список, содержащий два узла.
Вставка узла в определенное заданное место списка. Здесь и далее, мы не будем приводить фрагменты кода, так как они являются крупными. Позже мы с вами просто рассмотрим пример реализации односвязного списка целиком. А, сейчас, разберем операции над списком с помощью иллюстраций. Выделить память под новый узел. Записать в новый узел значение. Записать в указатель на следующий узел адрес узла, который должен располагаться после нового узла. Заменить в узле, который будет располагаться перед новым узлом, записанный адрес на адрес нового узла.
Удаление узла из списка. Записать адрес узла, следующего за удаляемым узлом, в указатель на следующий узел в узле, предшествующем удаляемому. Удалить узел, предназначенный для удаления.
Односвязный линейный список
Каждый узел однонаправленного (односвязного) линейного списка (ОЛС) содержит одно поле указателя на следующий узел. Поле указателя последнего узла содержит нулевое значение (указывает на NULL). 
Узел ОЛС можно представить в виде структуры
Основные действия, производимые над элементами ОЛС:
Инициализация ОЛС
Инициализация списка предназначена для создания корневого узла списка, у которого поле указателя на следующий элемент содержит нулевое значение.
Добавление узла в ОЛС
Функция добавления узла в список принимает два аргумента:
Процедуру добавления узла можно отобразить следующей схемой: 
Добавление узла в ОЛС включает в себя следующие этапы:
Таким образом, функция добавления узла в ОЛС имеет вид:
Возвращаемым значением функции является адрес добавленного узла.
Удаление узла ОЛС
В качестве аргументов функции удаления элемента ОЛС передаются указатель на удаляемый узел, а также указатель на корень списка.
Функция возвращает указатель на узел, следующий за удаляемым.
Удаление узла может быть представлено следующей схемой: 
Удаление узла ОЛС включает в себя следующие этапы:
Удаление корня списка
Функция удаления корня списка в качестве аргумента получает указатель на текущий корень списка. Возвращаемым значением будет новый корень списка — тот узел, на который указывает удаляемый корень.
Вывод элементов списка
В качестве аргумента в функцию вывода элементов передается указатель на корень списка.
Функция осуществляет последовательный обход всех узлов с выводом их значений.
Взаимообмен узлов ОЛС
В качестве аргументов функция взаимообмена ОЛС принимает два указателя на обмениваемые узлы, а также указатель на корень списка. Функция возвращает адрес корневого элемента списка.
Взаимообмен узлов списка осуществляется путем переустановки указателей. Для этого необходимо определить предшествующий и последующий узлы для каждого заменяемого. При этом возможны две ситуации:
При замене соседних узлов переустановка указателей выглядит следующим образом: 
При замене узлов, не являющихся соседними переустановка указателей выглядит следующим образом: 
При переустановке указателей необходима также проверка, является ли какой-либо из заменяемых узлов корнем списка, поскольку в этом случае не существует узла, предшествующего корневому.
Функция взаимообмена узлов списка выглядит следующим образом:
Комментариев к записи: 77
using namespace std;
struct NODE <
char value;
struct NODE* next;
>;
struct DbCircleList <
size_t size;
struct NODE* head;
>;
void addNode(DbCircleList* list, char elem)
<
NODE* newElem = new NODE;
newElem->value = elem;
if (list->size == 0)
<
list->head = newElem;
list->head->next = list->head;
>
else
<
struct NODE* temp;
temp = list->head;
list->head = newElem;
newElem->next = temp;
>
++list->size;
>
void printList(DbCircleList* list)
<
NODE* tmp = list->head;
cout «List values: » endl;
for ( int i = 0; i size; ++i)
<
cout «Value: » tmp->value endl;
tmp = tmp->next;
>
>
int main()
<
DbCircleList* list = new DbCircleList;
list->size = 0;
list->head = NULL ;
DbCircleList* list1 = new DbCircleList;
list1->size = 0;
list1->head = NULL ;
DbCircleList* list2 = new DbCircleList;
list2->size = 0;
list2->head = NULL ;
addNode(list, ‘b’);
addNode(list, ‘b’);
addNode(list, ‘3’);
addNode(list, ‘c’);
addNode(list, ‘3’);
addNode(list, ‘7’);
delete list;
delete list1;
delete list2;
return 0;
>
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
struct book
<
char name[30];
char author[30];
int num_page;
int year;
char style[30];
struct book* next;
>;
struct book* poperedbook, * element, * pershiy, * novii, * ostan;
void Stvorutu( void )
<
element = ( struct book*)malloc( sizeof ( struct book));
pershiy = element;
do
<
poperedbook = element;
ostan = poperedbook;
poperedbook->next = NULL ;
>
void hood( void )
<
element = pershiy;
int main()
<
SetConsoleCP(1251);
SetConsoleOutputCP(1251);
struct list <
int ptr;
list *next;
>;
void input_list(list *&first, int n) <
first = new list;
cinn >> first->ptr;
list *q = first;
for ( int i = 0; i next = new list;
q = q->next;
cin >> q->ptr;
>
q->next = 0;
>
void print_list(list *q) <
while (q) <
cout q->ptr » » ;
q = q->next;
>
cout endl;
>
void razbienie_list(list *&first) <
list *q = first;
list *chet = new list;
list *nechet = new list;
list *q1 = chet;
list *q2 = nechet;
list *w1 = q1;
list *w2 = q2;
while (p) <
if (q->ptr % 2) <
q2->ptr = p->ptr;
q2->next = new list;
w2 = q2;
q2 = q2->next;
>
else <
q1->ptr = p->ptr;
q1->next = new list;
q1 = q1;
q1 = q1->next;
>;
q = q->next;
>
w1->next = 0;
w2->next = 0;
>
int main() <
list *first = 0;
int n = 5;
input_list(first, n);
print_list(first);
razbienie_list(first);
print_list(first);
return 0;
>
int main()
<
char name[maxSize] = <'\0'>;
char type[maxSize] = <'\0'>;
double MaximumHeight;
double lifespan;
Wood* Head = nullptr;
int n;
//Вводим число деревьев, которые будем хранить в массиве
cout «Number of Wood = » ;
cin >> n;
//Вводим информацию о всех деревьях с помощью реализованной функции
for ( int i = 0; i // удаление элемента
cout » deleted Woods = » ;
cin >> lifespan;
DeleteWood(Head, WoodSearch(Head, lifespan)); // ЗДЕСЬ ОШИБКА
PrintWood(Head);
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
struct list
<
int field;
struct list* ptr;
>;
// Инициализация списка (ОЛС)
struct list* init( int a)
<
struct list* head = ( struct list*)malloc( sizeof ( struct list));
head->field = a;
head->ptr = NULL ;
return (head);
>
// Добавление элемента (возвращает добавленный элемент) (ОЛС)
struct list* addelem( struct list* lst, int number)
<
struct list* temp, * p;
temp = ( struct list*)malloc( sizeof ( struct list)); // выделение памяти под узел списка
p = lst->ptr; // временное сохранение указателя
lst->ptr = temp; // предыдущий узел указывает на создаваемый
temp->field = number; // сохранение поля данных добавляемого узла
temp->ptr = p; // созданный узел указывает на следующий элемент
return (temp);
>
// Удаление корня списка (возвращает новый корень) (ОЛС)
struct list* deletehead( struct list* root)
<
struct list* temp;
temp = root->ptr;
free(root);
return (temp); // новый корень списка
>
struct list* add( struct list* head, int data)
<
struct list* temp, * p;
p = head->ptr;
temp = ( struct list*)malloc( sizeof ( struct list));
head->ptr = temp;
temp->field = data;
temp->ptr = p;
return (temp);
>
struct list* t1 = t->ptr;
while (t1)
<
if (t1->field == v)
<
t->ptr = t1->ptr;
free(t1);
return ;
>
t = t1;
t1 = t1->ptr;
>
>
void sub( struct list* a, struct list* b)
<
struct list* p2;
for ( struct list* p2 = b; p2; p2 = p2->ptr)
del(a, p2->field);
/* struct list* p2;
p2 = b;
while (p2)
<
del(a, p2->field);
p2 = p2->ptr;
>*/
/* struct list* p1, * p2;
p1 = a;
p2 = b;
while (p1)
<
while (p2)
<
if (p1->field == p2->field)
deletelem(p1, p1->field);
p2 = p2->ptr;
>
p1 = p1->ptr;
>*/
>
int main()
<
setlocale(LC_ALL, «Russian» );
/* struct list* p1 = ( struct list*)malloc( sizeof ( struct list));
struct list* p2 = ( struct list*)malloc( sizeof ( struct list));
p1 = init(5);
add(p1, 6);
add(p1, 9);
p2 = init(6);
add(p2, 7);
Список
Связный список (англ. List) — структура данных, состоящая из элементов, содержащих помимо собственных данных ссылки на следующий и/или предыдущий элемент списка. С помощью списков можно реализовать такие структуры данных как стек и очередь.
Содержание
Односвязный список [ править ]
Простейшая реализация списка. В узлах хранятся данные и указатель на следующий элемент в списке.
Двусвязный список [ править ]
Также хранится указатель на предыдущий элемент списка, благодаря чему становится проще удалять и переставлять элементы.
XOR-связный список [ править ]
В некоторых случаях использование двусвязного списка в явном виде является нецелесообразным. В целях экономии памяти можно хранить только результат выполнения операции Xor над адресами предыдущего и следующего элементов списка. Таким образом, зная адрес предыдущего элемента, мы можем вычислить адрес следующего элемента.
Циклический список [ править ]
Первый элемент является следующим для последнего элемента списка.
Операции на списке [ править ]
Рассмотрим базовые операции на примере односвязного списка.
Вставка [ править ]
Очевиден случай, когда необходимо добавить элемент ( [math]newHead[/math] ) в голову списка. Установим в этом элементе ссылку на старую голову, и обновим указатель на голову.
Поиск [ править ]
Удаление [ править ]
Для того, чтобы удалить голову списка, переназначим указатель на голову на второй элемент списка, а голову удалим.
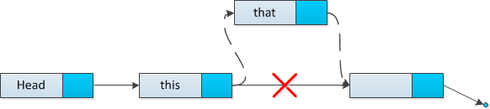
Удаление элемента после заданного ( [math]thisElement[/math] ) происходит следующим образом: изменим ссылку на следующий элемент на следующий за удаляемым, затем удалим нужный объект.
Поиск цикла в списке [ править ]
Для начала необходимо уметь определять — список циклический или нет. Воспользуемся алгоритмом Флойда «Черепаха и заяц». Пусть за одну итерацию первый указатель (черепаха) переходит к следующему элементу списка, а второй указатель (заяц) на два элемента вперед. Тогда, если эти два указателя встретятся, то цикл найден, если дошли до конца списка, то цикла нет.
Поиск длины хвоста в списке с циклом [ править ]
Наивные реализации [ править ]
Реализация за [math]O(n^2)[/math] [ править ]
Будем последовательно идти от начала цикла и проверять, лежит ли этот элемент на цикле. На каждой итерации запустим от [math]pointMeeting[/math] вперёд указатель. Если он окажется в текущем элементе, прежде чем посетит [math]pointMeeting[/math] снова, то точку окончания (начала) хвоста нашли.
Реализация за [math]O(n \log n)[/math] [ править ]
Эффективная реализация [ править ]
Доказательство корректности алгоритма [ править ]
[math]f_1(n) = L + (n-L) \bmod N[/math]
[math]f_2(n) = L + (2n-L) \bmod N[/math]
[math]Q = L + (1-k) N[/math]
Пусть [math]L = p N + M, 0 \leqslant M \lt N[/math]
[math]L \lt k N \leqslant L + N[/math]
[math]pN + M \lt kN \leqslant (p+1)N + M[/math] откуда [math]k = p + 1[/math]
Задача про обращение списка [ править ]
Для того, чтобы обратить список, необходимо пройти по всем элементам этого списка, и все указатели на следующий элемент заменить на предыдущий. Эта рекурсивная функция принимает указатель на голову списка и предыдущий элемент (при запуске указывать [math]NULL[/math] ), а возвращает указатель на новую голову списка.
Алгоритм корректен, поскольку значения элементов в списке не изменяются, а все указатели [math]next[/math] изменят свое направление, не нарушив связности самого списка.