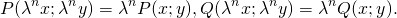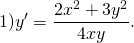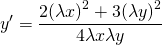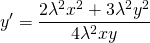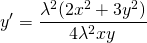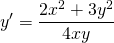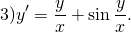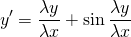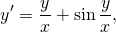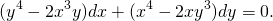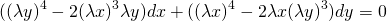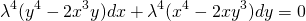Однородное уравнение что значит
Однородные уравнения (ЕГЭ 2022)
В этой статье ты научишься решать однородные уравнения.
В частности, тригонометрические и показательные.
И это не так сложно, как выглядит!
Потому что алгоритм решения однородных уравнений один и тот же!
Для этого эти уравнения и выделили в одну группу – чтобы было легче решать. По одному алгоритму.
Читай статью, решай примеры и все поймешь!
Однородные уравнения — коротко о главном
Определение однородных уравнений
Однородные уравнения – это уравнения вида \( <
_<0>>< ^ >+< _<1>>< ^ >y+< _<2>>< ^ >< ^<2>>+…+< _ >x< ^ >+< _ >< ^ >=0\) с двумя неизвестными, в каждом из слагаемых которых одинаковая сумма степеней этих неизвестных.
Решение всех однородных уравнений сводится к делению на одну из неизвестных в степени \( n\) и дальнейшей заменой переменных.
Алгоритм решения однородных уравнений
Однородные уравнение — подробнее
Что такое однородные уравнения? Давай посмотрим на определение.
Однородные уравнения – это уравнения вида \( <
_<0>>< ^ >+< _<1>>< ^ >y+< _<2>>< ^ >< ^<2>>+…+< _ >x< ^ >+< _ >< ^ >=0\) с двумя неизвестными, в каждом из слагаемых которых одинаковая сумма степеней этих неизвестных.
Совершенно пугающее определение, поэтому разберемся на примере.
Пример №1
Это уравнение однородное. Почему? Давай посмотрим на определение.
Стоп! Давай все-таки попытаемся разобраться в этой громоздкой формуле.
На первом месте должна идти первая переменная в степени \( n\) с некоторым коэффициентом. В нашем случае это \( 1\cdot <^<2>>,\ \ k=1,\ \ x=a,\ \ n=2\)
Дальше идет первая переменная в степени \( n-1\) и вторая переменная в первой степени.
Как мы выяснили, \( n=2\), значит здесь степень \( n-1=1\) при первой переменной \( \left( a \right)\) – сходится.
Первая переменная \( \left( a \right)\) в степени \( n-2=0\), и вторая переменная \( \left( b \right)\) в квадрате, с коэффициентом \( \left( 3 \right)\). Это последний член уравнения.
Как видишь, наше уравнение подходит под определение в виде формулы.
Давай рассмотрим вторую (словесную) часть определения.
…с двумя неизвестными, в каждом из слагаемых которого одинаковая сумма степеней этих неизвестных.
У нас две неизвестные \( (a\) и \( b)\). Здесь сходится.
Рассмотрим все слагаемые. В них сумма степеней неизвестных должна быть одинакова.
\( 3<^<2>>\) — сумма степеней равна \( 2\).
Как видишь, все сходится! Это однородное уравнение.
Теперь давай потренируемся в определении однородных уравнений.
Определи какие из уравнений — однородные
Однородные уравнения — уравнения под номерами:
Рассмотрим отдельно \( 11\) уравнение.
Если мы разделим каждое слагаемое на разложим каждое слагаемое, то получим:
А это уравнение полностью попадает под определение однородных уравнений.
Как решать однородные уравнения
Решение всех однородных уравнений сводится к делению на одну из неизвестных в степени \( n\) и дальнейшей заменой переменных.
Пример №2
Найдите \( \displaystyle \frac
Разделим уравнение на \( <
Нужно всегда помнить, что делить (и умножать) на переменную мы можем только тогда, когда мы уверены, что эта переменная не может быть равна \( 0\). Например, если нас просят найти \( \frac
\), то мы сразу понимаем, что \( y\ne 0\), поскольку на \( 0\) делить нельзя.
Когда это не так очевидно, необходимо отдельно проверять случай, когда эта переменная равна \( 0\).
У нас по условию y не может быть равен \( 0\). Поэтому мы можем смело делить на \( <
Произведя замену \( t=\frac
Так как это приведенное квадратное уравнение, воспользуемся теоремой Виета:
Произведя обратную замену, получаем ответ
Ответ: \( 2;5\)
Пример №3
Нужно найти: \( \displaystyle \ \frac
Решение:
Разделим уравнение на \( <
Произведем замену \( \displaystyle t=\frac
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Пример №4
Здесь нужно не делить, а умножать.
Умножим все уравнение на \( <
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Решение однородных тригонометрических уравнений
Решение однородных тригонометрических уравнений ничем не отличается от способов решения, описанных выше.
Только здесь, помимо прочего, нужно немного знать тригонометрию. И уметь решать тригонометрические уравнения (для этого можешь прочитать раздел «Тригонометрические уравнения»).
Рассмотрим такие уравнения на примерах.
Пример №5
Решите уравнение \( <<\sin >^<2>>x-3\sin x\cdot \cos x-4<<\cos >^<2>>x=0\).
Мы видим типичное однородное уравнение: \( \sin x\) и \( \cos x\) – это неизвестные, а сумма их степеней в каждом слагаемом равна \( 2\).
Подобные однородные уравнения решаются не сложно, но перед тем, как разделить уравнения на \( <<\cos >^<2>>x\), рассмотрим случай, когда \( \cos x=0\)
В этом случае уравнение примет вид: \( <<\sin >^<2>>x=0\), значит \( \sin x=0\). Но синус и косинус не могут одновременно быть равны \( 0\), ведь по основному тригонометрическому тождеству \( <<\cos >^<2>>x+<<\sin >^<2>>x=1\). Поэтому \( \cos x\ne 0\), и на него можно смело делить:
Сделаем замену \( t=tgx\) и решим квадратное уравнение:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Пример №6
Решите уравнение \( 5<<\sin >^<2>>x-2\sin x\cdot \cos x-3<<\cos >^<2>>x=0\).
Как и в примере \( 5\), нужно разделить уравнение на \( <<\cos >^<2>>x\).
Рассмотрим случай, когда \( \cos x=0\) :
Но синус и косинус не могут одновременно быть равны \( 0\), ведь по основному тригонометрическому тождеству \( <<\cos >^<2>>x+<<\sin >^<2>>x=1\).
Поэтому \( \cos x\ne 0\).
Сделаем замену \( t=tgx\) и решим квадратное уравнение:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Решение однородных показательных уравнений
Однородные уравнения решаются так же, как рассмотренных выше. Если ты забыл, как решать показательные уравнения – посмотри соответствующий раздел («Показательные уравнения»)!
Рассмотрим несколько примеров.
Пример №7
Мы видим типичное однородное уравнение, с двумя переменными и суммой степеней \( 2x\). Разделим уравнение на \( <<18>^<2x>>\):
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Пример №8
Разделим уравнение на \( <<16>^<2x>>\):
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Пример №9
На примере этой задачи повторим, что такое однородные уравнения и как их решать.
Здесь можно заметить любопытную вещь: если поделить каждое слагаемое на \( <^<2>>\), получим:
То есть, теперь нет отдельных \( a\) и \( b\), – теперь переменной в уравнении является искомая величина \( \frac\). И это обычное квадратное уравнение, которое легко решить с помощью теоремы Виета: произведение корней равно \( 2\), а сумма \( 3\) – это числа \( 2\) и \( 1\).
Ответ: \( 1;\text< >2.\)
называется однородным.
То есть это уравнение с двумя неизвестными, в каждом слагаемом которого одинаковая сумма степеней этих неизвестных. Например, в примере выше эта сумма равна \( 2\).
Решение однородных уравнений осуществляется делением на одну из неизвестных в этой степени:
И последующей заменой переменных: \( t=\frac
Чаще всего нам будут встречаться уравнения второй степени (то есть квадратные), а их решать мы умеем:
\( \displaystyle \Leftrightarrow\ a<
Отметим, что делить (и умножать) все уравнение на переменную можно только если мы убеждены, что эта переменная не может быть равна нулю!
Например, если нас просят найти \( \displaystyle \frac
В случаях, когда это не так очевидно, необходимо отдельно проверять случай когда эта переменная равна нулю. Например:
Решите уравнение \( <<\sin >^<2>>x+3\sin x\cdot \cos x+2<<\cos >^<2>>x=0\).
Пример №10
Видим здесь типичное однородное уравнение: \( \sin x\) и \( \cos x\) – это неизвестные, а сумма их степеней в каждом слагаемом равна \( 2\).
Но, прежде чем разделить на \( <<\cos >^<2>>x\) и получить квадратное уравнение относительно \( \displaystyle \frac<\sin x><\cos x>\), мы должны рассмотреть случай, когда \( \cos x=0\).
Как определить однородное уравнение
Дифференциальное уравнение 1-го порядка P(x;y)dx+Q(x;y)dy=0 называется однородным, если P(x;y) и Q(x;y) — однородные функции одинакового измерения, то есть
Как определить, что дифференциальное уравнение — однородное? На практике проверку уравнения на однородность проводят следующим образом: вместо каждого x подставляют λx, вместо каждого y — λy. При этом y’, dx и dy не трогают. После этого упрощают уравнение. Если после упрощения удается сократить на λ (или n- ю степень λ) и получить исходное уравнение, то это и означает, что данное уравнение является однородным уравнением 1-го порядка.
Другая форма записи: y’=f(x;y). Это уравнение является однородным, если функция f(x;y) является однородной функцией нулевого порядка. Это означает, что f(λx;λy)=f(x;y).
Подставляем вместо каждого x λx, вместо каждого y — λy:
Выносим лямбда в квадрате за скобки и сокращаем на него:
Пришли к исходному уравнению, а это значит, что данное уравнение — однородное.
2) (x-y)ydx-x²dy=0.
Подставляем вместо каждого x λx, вместо каждого y — λy: (λx-λy)λydx-(λx)²dy=0. Теперь выносим общий множитель λ² за скобки: λ²((x-y)ydx-x²dy)=0. Делим обе части уравнения на λ²:
(x-y)ydx-x²dy=0. Пришли к исходному уравнению, значит, это уравнение — однородное. (Здесь P(x;y) и Q(x;y) — однородные функции 2й степени).
Наличие дроби y/x уже косвенно указывает на то, что уравнение может быть однородным. Проверим, так ли это:
После сокращения на λ получаем исходное уравнение:
а это значит, что данное уравнение является однородным.
Подставляем вместо каждого x λx, вместо каждого y — λy:
Делим обе части уравнения на лямбда в 4й степени:
Получили исходное уравнение, а значит, оно является однородным. (Здесь P(x;y) и Q(x;y) — однородные функции 4й степени).
Дифференциальное однородное уравнение: особенности и решение
Однородные уравнения
| F = | g 3 +r 3 | A = | d 2 + w 2 |
| 3g 3 + 5r 2 g | 2dw |
Чтобы убедиться в их однородности, достаточно аргументы функции F или A умножить на какой-либо коэффициент и посмотреть, не сократится ли он.
Замена e(t) = f(1, t)
Выше говорилось о том, что дифференциальные уравнения с однородными функциями сводятся к разделяющимся за счет замены. Для объяснения этого рассмотрим лемму.
Доказывается данная лемма тривиальным образом: для этого просто нужно положить k = 1/x для всех ненулевых x.
Применение замены в решение y’ = f(x, y)
Интегрируя, получим решение E = ln|x| + C.
Заметка
Рассмотрим, почему вышеописанная замена работает при решении однородных дифференциальных уравнений. Для этого возьмем общее решение E = ln|x| + C и заменим x на kx и y на ky: E = ln|kx| + C = ln(k) + ln|x| + C. В свою очередь выражение ln(k) + C может быть представлено как W, и тогда решение будет выглядеть как E = ln|x| + W.
Получается, что замена x на kx и y на ky приводит лишь к замещению одного решения другим, но из того же класса. Иными словами, другое решение также удовлетворяет исходному уравнению. Описанное свойство на координатной плоскости называется гомотетией, т. е. интегральные кривые однородных дифференциальных уравнений переходят друг в друга.
Пример 1
Дано уравнение l 2 + ml + m 2 l’ + m 2 = 0. Найдем его решение. Неопытный глаз может по ошибке торопливо заключить, что данное уравнение не однородно, так как подстановка km вместо m и kn вместо n не дает исходное уравнение. Ошибка в данном случае заключается в том, что уравнение предварительно не было разрешено относительно производной n’. Сделаем.
В данном виде легко определить, что уравнение однородно.
| f(km, kl) = | (-1)[(km) 2 + (kl) 2 + k 2 ml] | = | (-1)(l 2 +ml+m 2 )k 2 | = | f(m, l) |
| (km) 2 | m 2 k 2 |
Приступим к решению, совершив замену l/m = v. Получим l = vm и l’ = mv’ + v. Подставим эти значения в уравнение:
Из получившегося уравнения в дифференциальной форме легко находится общий интеграл:
Проведем обратную замену:
Линейные дифференциальные уравнения
Часто однородные дифференциальные уравнения путают с линейными. Для полноты вопроса рассмотрим немного и этот класс. Итак, линейным называется дифференциальное уравнение, в котором функция и ее производная располагаются в линейной зависимости, т. е. получаем уравнение, которому присущ следующий вид:
Для разрешения этого уравнения относительно y’ необходимо рассмотреть все корни o(x). Положим, что для некоторого числа o(x0) = 0, тогда одним из решений описанного уравнение будет x0, т.к. получаем o(x0)dy = 0 и dx = 0. Это становится очевидным, если записать дифференциальную форму уравнения, умножив на dx обе части: o(x)dy + w(x)ydx = e(x)dx.
Исключив нулевые значения o(x), для оставшихся значений x записываем уравнение в разрешенном виде, поделив его на o(x).
Решение линейных дифференциальных уравнений
В общем случае линейное уравнение (неоднородное) решается в несколько этапов:
Еще одна путаница однородных уравнений возникает при рассмотрении однородных систем уравнений. Однако это другой вопрос, рассмотрение которого выходит за пределы данной статьи.
Примеры
Дана задача. Нужно найти решение.
| y’ + | ty | = | t |
| t 2 +1 | √(t 2 +1) |
Очевидно, данное уравнение неоднородно, поэтому решим сначала следующее уравнение:
Следует отметить, что одним из решений уравнения является y = 0. Нахождение общего решения происходит через дифференциальную форму, которая позволяет воспользоваться разделением переменных:
| dy | = | (-1)tdt |
| y | t 2 +1 |
Решение неоднородного уравнения выполним другим, аналогичным способом, который называется методом вариации постоянной, или метод Лагранжа. Опишем его теоретически.
Применяя метод Лагранжа для нашей задачи, положим:
| y | = | x 2 | + | D |
| 2√(t 2 +1) | √(t 2 +1) |
Мы рассмотрели способы решения линейных однородных уравнений.
16. Однородные и линейные уравнения первого порядка
Прежде всего, рассмотрим простые и важные классы уравнений первого порядка, приводящихся к уравнениям с разделяющимися переменными.
I. Однородные уравнения.
Называется однородным, если функция 
может быть представлена как функция отношения своих аргументоВ:
Однородное, так как его можно записать в виде
В общем случае переменные в однородном уравнении не разделяются. Однако, вводя вспомогательную неизвестную функцию U по формуле
или 
Мы сможем преобразовать однородное уравнение в уравнение с разделяющимися переменными.
И уравнение 
прИНимает вид
, т. е. 
После интегрирования получаем:
Найдя отсюда выражение для И как функции от Х, и возвращаясь к переменной 
, получим искомое решение однородного уравнения.
Чаще всего не удается просто найти явное выражение для И. Тогда после интегрирования следует в левую часть вместо U ПодстаВить 
; в результате мы получим решение уравнения в неявном виде.
Разумеется, мы предполагаем, что 
. Если 
, то 
и не нужно делать никаких преобразований, ибо само заданное уравнение 
— с разделяющимися переменными.
Нет необходимости запоминать полученные выше формулы: в каждом примере нетрудно проделать полностью указанное преобразование.
Пример. Найдем решение однородного уравнения
Замена 
приводит к уравнению
или 
Разделяя переменные, находим:
, или 
Возвращаясь к перемеННой У, приходим к общему решению:
II. Линейные уравнения. Вторым часто встречающимся типом уравнений первого порядка явлЯЕтся линейное уравнение.
Определение. Уравнение вида
(*)
Т. Е. линейное относительно искомой фуНКции и ее производНОй, называется линейным.
Здесь Р(Х) и Q(Х) — известные функции независимой переменной Х.
Уравнение (*) сводится к двум уравнениям с разделяющимися переменными путем следующего искусственного приема. Запишем функцию У в виде произведения двух функций: 
. одной из них мы можем распорядиться совершенно произвольно; при этом вторая должна быть определена в зависимости от первой таким образом, чтобы их произведение удовлетворяло данному линейному уравнению. Свободой выбора одной иЗ функций U и N мы воспользуемся для максимального упрощения уравнения, получающегося после замены.
Из равенства 
находим производную У’:
Подставляя это выражение в уравнение (*), имеем:
, или 
.
Выберем в качестве N какое-нибудь частное решение уравнения
. (**)
Тогда для отыскания U получим уравнение
. (***)
Сначала найдем N из уравнения (**). Разделяя переменные, имеем:
и 
.
Как и раньше, под неопределенным интегралом здесь понимается Какая-нибудь одна первообразная от функции Р(Х), т. е. N является вполне определенной функцией от Х.
Зная N, находим далее И из уравнения (***):
Здесь мы уже берем для U все первообразные. По И и N найдем искомую функцию У:
Полученная формула дает общее решение линейного уравнения (*).
Положение не изменится, если мы прибавим произвольную постоянную к интегралу в показателе. В самом деле, эта вторая произвольная постоянная в конечном счете исчезнет, так как один множитель будет содержать ее в знаменателе, а другой — в числителе.
Можно решать задачу с помощью определенных интегралов с переменным верхним пределом. При этом
Частное решение, соответствующее начальному условию 
, Получается отсюда при 
.
Как и раньше, мы не настаиваем на запоминании общей формулы. Следует помнить лишь способ решения и применять его в каждом конкретном случае.
Пример. Решим уравнение 
Положим 
, тогда 
. Имеем: 
или 
Пусть 
. Отсюда 
и, значит, 
Т. е. 
Следовательно, 
откуда 
и, значит, 
Имеем окончательно:
.
Рассмотрим одну важную задачу электротехники, которая приведет нас к линейному дифференциальному уравнению первого порядка. Пусть ЭЛектрическая цепь имеет сопротивление R и самоиндукцию L.
Если через I обозначить силу тока в цепи, а через Е электродвижущую силу, то, как известно из физики,
.
Считая, что Е является известной функцией времени, получаем линейное уравнение, которое запишем в виде
Проинтегрируем это уравнение в предположении, что 
при начальном условии 
. Это означает, что мы включаем в цепь, в которой не было тока, постоянную электродвижущую силу. Воспользовавшись общей формулой, выраженной при помощи определенных интегралов, получим:
Или, выполняя интегрирование,
.
Ток I слагается как бы из двух токов: тока 
, соответствующего закону Ома, и экстратока замыкания 
, протекающего в обратном направлении. Экстраток замыкания быстро стремится к нулю, и поэтому в цепи довольно скоро устанавливается постоянный ток. Еще проще решается задача о размыкании цепи. В этом случае мы считаем, что 
и 
. Тогда получается уравнение с разделяющимися переменными 
Решая его, ПолуЧиМ 
— экстраток размыкания. Скорость СтремЛения экстратока к нулю зависит от отношения 
: чем это отношение больше, тем быстрее экстраток затухает.
Рекомендуем читателю самостоятельно решить задачу в случае, когда электродвижущая сила Е синусоидальна, т. е. когда 
.