Один треугольник находится внутри другого докажите что его периметр меньше
Треугольник лежит внутри треугольника. Его периметр тоже меньше?
Треугольник задан координатами его вершин. Вычислить периметр, площадь треугольника
Собственно вот сама задача: Треугольник задан координатами его вершин. Вычислить периметр, площадь.
Определить, что точка лежит лежит внутри прямоугольника или на одной из его сторон
составит программу печатающую значение TRUE если указанное высказывание является истинным, и FALSE.
Определить, что точка лежит лежит внутри прямоугольника или на одной из его сторон
составит программу печатающую значение TRUE если указанное высказывание является истинным, и FALSE.
Решение
Решение
Решение
Решение
Можно было, конечно, вместо рисунков просто написать два слова «неравенство треугольника» и отправить ТС-а продираться сквозь дебри геометрии самостоятельно.
Байт, спасибо
(а где блондинка?)
jogano,
спасибо. Вы так здорово разбираетесь в геометрии, что вам можно
только позавидовать (Нет, это хорошая белая зависть). А вот применить
эллипс мне даже в голову не пришло. Хотя я понимал конечно, что тот
случай, когда одна сторона треугольника будет лежать на другой стороне
треугольника требует особого рассмотрения. Ведь нигде не сказано, что
этот треугольник можно подвинуть или повернуть или вообще изменить.
(например он просто вписан, без возможности что-либо с ним сделать).
Один треугольник находится внутри другого докажите что его периметр меньше
Задача 1: a, b, c – стороны треугольника. a = 3,17, b = 0,75, c – целое число. Найти c.
Задача 2: Доказать, что в четырехугольнике диагональ меньше половины периметра.
Задача 3:
a) Доказать, что в четырехугольнике любая сторона меньше суммы остальных.
b) То же для любого многоугольника.
Задача 4: Есть 7 прутьев длиннее 9 см, но короче 1 м. Доказать, что из трех из них можно составить треугольник.
Задача 5: Найти точку на данной прямой, сумма расстояний от которой до двух данных точек минимальна.
Задача 6: Найти точку внутри четырехугольнике, сумма расстояний от которой до вершин минимальна.
Задача 7: A и B – точки внутри многоугольника. Доказать, что расстояние между ними меньше половины периметра многоугольника.
Задача 8: Доказать, что в выпуклом четырехугольнике сумма диагоналей больше суммы противоположных сторон.
Задача 9: Доказать, что в выпуклом четырехугольнике сумма диагоналей больше полупериметра, но меньше периметра.
Задача 10: Доказать, что в выпуклом n-угольнике (n > 3) не больше двух сторон, которые длиннее любой диагонали.
Задача 11: Один треугольник лежит внутри другого. Доказать, что периметр внутреннего треугольника меньше периметра внешнего
a) если треугольники имеют общую сторону и угол.
b) если треугольники имеют общий угол.
c) если треугольники имеют общую сторону.
Задача 12: Один выпуклый многоугольник лежит внутри другого. Доказать, что периметр у внутреннего многоугольника меньше, чем у внешнего.
Задача 13: Доказать, что перпендикуляр короче наклонной.
Задача 14: В лесу 100 деревьев. Высота любого больше 10, но меньше 40 метров. Расстояние между любыми двумя деревьями не больше разности их высот. Доказать, что лес можно обнести забором длинны 81 метр.
Задача 15: Доказать, что сумма расстояний от точки внутри треугольника до его вершин больше его полупериметра, но меньше периметра.
Задача 16: Доказать, что в выпуклом 5-угольнике сумма диагоналей больше периметра, но меньше удвоенного периметра.
Задача 17: a) Доказать, что из двух наклонных короче та, которая ближе к перпендикуляру.
b) В треугольнике ABC точка L лежит на стороне BC. Доказать, что AL b a)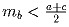 
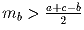
, b) 
.
Задача 19: Дан угол и точки A и B внутри него. Найти X и Y на сторонах угла такие, что длина пути AXYB минимальна.
Задача 20: На столе лежат несколько разных, но правильно идущих часов. Доказать, что найдется момент, когда сумма расстояний от центра стола до концов минутных стрелок больше суммы расстояний от центра стола до центров часов.
Задача 21: Доказать, что в любом выпуклом 5-угольнике есть три диагонали, из которых можно составить треугольник.
Задача 22: Многоугольник, вырезанный из бумаги, сложили, перегнув по одной линии. Доказать, что в результате этого периметр уменьшился.
Задача 23: Стороны треугольника выражаются целыми числами. Может ли его медиана иметь длину 1?
И. В. Яковлев | Материалы по математике | MathUs.ru
внутри треугольника располагаться треугольник большего периметра? Или внутри тетраэдра
тетраэдр большего периметра?
Данный листок посвящён различным подходам к одной геометрической задаче, которая
была предложена в далёком 1982 году на Всесоюзной олимпиаде по математике1.
Задача. Вершины тетраэдра KLM N лежат внутри, на гранях или на рёбрах другого тетраэдра ABCD. Докажите, что сумма длин всех рёбер тетраэдра KLM N меньше, чем 4/3 суммы длин всех рёбер тетраэдра ABCD.
Эта задача была четвёртой в варианте второго дня, и решили её лишь четыре человека из пятидесяти трёх (среди них был Григорий Перельман в то время десятиклассник, а ныне один из крупнейших современных математиков).
При этом было найдено три различных решения:
одно чисто геометрическое, не требующее ничего кроме неравенства треугольника; второе использовало усреднение проекций векторов на различные прямые, а третье базировалось на идее выпуклой оптимизации и по сути совпадало с авторским. Со всеми тремя решениями мы и познакомимся.
Задача 1. Один тетраэдр расположен внутри другого.
Может ли периметр (т. е. сумма длин рёбер) внутреннего тетраэдра быть больше периметра внешнего?
Задача 2. Один треугольник расположен внутри другого.
Может ли периметр внутреннего треугольника быть больше периметра внешнего?
Геометрическое решение Вначале рассмотрим решение, не выходящее за рамки школьной геометрии и требующее минимума технических средств.
Задача 3. Назовём грань тетраэдра наибольшей, если её периметр не меньше периметра каждой из остальных граней.
Докажите, что периметр тетраэдра не превосходит удвоенного периметра его наибольшей грани.
Задача 4. Треугольник расположен внутри выпуклого многоугольника.
Докажите, что периметр треугольника не превосходит периметра многоугольника.
Задача 5. Какой фигурой может быть проекция тетраэдра на плоскость? Докажите, что периметр фигуры-проекции меньше 2/3 суммы длин проекций рёбер тетраэдра на эту плоскость.
Задача 6. Решите Задачу.
Уровень Всесоюзной олимпиады был выше нынешней Всероссийской, так как помимо России в ней участвовали лучшие школьники союзных республик: Украины, Белоруссии, Закавказья, Прибалтики. (сейчас бывшие республики сами по себе являются сильными математическими странами и берут медали на Международной математической олимпиаде). Из победителей и призёров союза можно было составить несколько полноценных команд на межнар, а сборная СССР на Международной олимпиаде обычно занимала 1–3 места (чаще всего первое).
Усреднение проекций вектора Сначала нужно обсудить понятие среднего значения функции, которое служит далеко идущим обобщением понятия среднего арифметического нескольких чисел.
Пусть функция f (x) задана на
Пользуясь тем, что дуги разбиения очень малы, мы можем аппроксимировать окружность многоугольником и считать, что lk есть длина стороны многоугольника (то есть длина хорды, стягивающей соответствующую дугу), а точка Mk выбрана в середине этой стороны. Такой приём поможет найти интересующее нас среднее значение чисто геометрически, не прибегая к вычислению интеграла.
Задача 9. В вертикальной плоскости расположено проволочное кольцо радиуса R.
На проволоку насажена бусинка массой m. Вычислите работу силы тяжести при соскальзывании бусинки из верхней точки кольца в нижнюю.
среднее значение длины проекции вектора на Установленный замечательный результат всевозможные прямые пропорционально длине вектора и не зависит от его направления позволяет доказать следующее утверждение.
Задача 11. На плоскости даны две системы векторов: a1,.
. am и b1. bn. Известно, что сумма длин проекций векторов первой системы на любую прямую не превосходит суммы длин проекций векторов второй системы на ту же прямую. Докажите, что сумма длин векторов первой системы не превосходит суммы длин векторов второй системы.
Задача 12. Один выпуклый многоугольник расположен внутри другого.
Докажите, что периметр внутреннего многоугольника не превосходит периметра внешнего.
Задача 14. В пространстве даны две системы векторов: a1,.
. am и b1. bn. Известно, что сумма длин проекций векторов первой системы на любую прямую не превосходит суммы длин проекций векторов второй системы на ту же прямую. Докажите, что сумма длин векторов первой системы не превосходит суммы длин векторов второй системы.
Задача 15. Один выпуклый многогранник расположен внутри другого.
Докажите, что площадь поверхности внутреннего многогранника не превосходит площади поверхности внешнего.
Задача 16. Пусть проекция тетраэдра на некоторую прямую является отрезком длины l.
Докажите, что сумма длин проекций рёбер тетраэдра на эту прямую не меньше 3l и не больше 4l.
Задача 17. Решите Задачу.
Выпуклая оптимизация Для начала разберёмся с важнейшим понятием выпуклой функции.
Определение. Множество точек плоскости или пространства называется выпуклым, если вместе с любой парой своих точек оно целиком содержит отрезок, их соединяющий.
Определение. Функция f (x) называется выпуклой на промежутке I R, если
для любых x1, x2 I и любых неотрицательных, µ таких, что + µ = 1.
Задача 18. Пусть a b и x = a + (1 )b.
Убедитесь, что если пробегает отрезок [0; 1], то x пробегает отрезок [a; b].
Задача 19. Надграфиком функции y = f (x) называется множество
(это множество точек, расположенных над графиком, включая сам график). Докажите, что функция выпукла тогда и только тогда, когда её надграфик выпуклое множество.
Задача 20. Докажите, что сумма функций, выпуклых на промежутке I, также является выпуклой на I функцией.
Задача 21. Докажите, что наибольшее значение функции, выпуклой на отрезке, достигается на границе этого отрезка.
Мы определили понятие выпуклости для функции, заданной на точках прямой. Можно обобщить его для функции точки плоскости или пространства.
Рассмотрим для определённости трёхмерное пространство E3 (ведь именно оно нужно для нашей Задачи). Зафиксируем начало координат O и каждой точке X E3 поставим в соответствие её радиус-вектор x = OX. Тогда функцию f (X) точки X можно рассматривать как функцию f (x) радиус-вектора этой точки.
Определение. Пусть V E3 выпуклое подмножество трёхмерного пространства. Функция f (x) называется выпуклой на V, если
для любых X1, X2 V и любых неотрицательных, µ таких, что + µ = 1.
Задача 22. Пусть f (X) выпуклая функция точки X.
Пусть X пробегает некоторый отрезок.
Докажите, что наибольшее значение f достигается на границе этого отрезка.
Для решения Задачи нас интересует выпуклость лишь одной функции расстояния.
Задача 23. Докажите, что функция f (x) = |x| является выпуклой (на всём пространстве E3 ).
Задача 25. Пусть A, B, C фиксированные точки пространства.
Докажите, что периметр тетраэдра ABCX является выпуклой функцией точки X.
Задача 26. Решите Задачу.
«НАУЧНЫЙ ВЕСТНИК ДГМА № 1 (7Е), 2011 106 ОПРЕДЕЛЕНИЕ КАЧЕСТВА И НАДЁЖНОСТИ МНОГОЛЕЗВИЙНОГО ИНСТРУМЕНТА Клименко Г. П. Разработана иерархическая система свойств, составляющих качества многолезвийных сборных инструментов. Исследована износостойкость фрез с пластинами, изготовленными разными фирмами. На основании теории надёжности получ. »
«РАБОЧАЯ ПРОГРАММА ПО ХИМИИ СРЕДНЕГО ОБЩЕГО ОБРАЗОВАНИЯ (БАЗОВЫЙ УРОВЕНЬ) Пояснительная записка Рабочая программа составлена в соответствии с ФК ГОС 2004.На основе: 1) Примерной образовательной программы среднего общего образования по химии, МО РФ 2004;2) Закона Российской Федерации от 29.12.2012 №273 ФЗ «Об образовании в Российской Феде. »
«Введение Теоретическая и статистическая вероятность Зависимые и независимые события Формула Бернулли КОМБИНАТОРНАЯ ВЕРОЯТНОСТЬ Тема 5 Перевод осуществлен при поддержке IT Akadeemia Jaan Penjam, email: jaan@cs.ioc. »
«Расшифровка «Генриха». Второго, с помощью «Расшифрованного Нострадамуса» Дмитрия и Надежды Зима С учётом математической расшифровки предсказаний Нострадамуса, произведённой авторами, выяснилось, что некоторые катрены, посвящённые Нострадамусом будущему «Генриху», Второму, может расшифровать только. »
«УДК 082 ББК 94 Z 40 Wydawca: Sp. z o.o. «Diamond trading tour» Druk I oprawa: Sp. z o.o. «Diamond trading tour» Adres wydawcy I redacji: Warszawa, ul. Wyszogrodzka,16 e-mail: info@conferenc.pl Cena (zl.): bezpatnie Zbir raportw naukowych. Z 40 Zbir r. »
«Петрология, геохимия, геохронология ЛИТЕРАТУРА Алфимова Н.А., Матреничев В.А. Континентальное выветривание в раннем докембрии: особенности минеральных преобразований и состав гипергенных растворов. Литология и полезные ископаемые, М., 2006, в печати (№4) Ахм. »
«Методологической основой рабочей программы является перспективное планирование, составленное по примерной основной общеобразовательной программе дошкольного образования «От рождения до школы» под ред. Н.Е. Вераксы, Т.С. Комаровой, М.А. Васильев. »
«.’ ‘.-у/• с5t-J ТЕЗИСЫ Д ОКЛАД ОВ XIX ВСЕСОЮЗНОГО СОВЕЩАНИЯ ПО ФИЗИКЕ ВЗАИМОД ЕЙСТВИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ С КРИСТАЛЛАМИ Москва, 29 31 мая 1989 г. Издательство Московского Университета АКАДЕМИЯ НАУК СССР МОСКОВСКИЙ ОРДЕНА ЛЕНИН,’,, ОРДЕНА. »
«IFCS 02в Пункт 3 повестки дня IFCS/FORUM III/02w МФХБ/ФОРУМ III/02в Партнерство в интересах глобальной химической безопасности Original: English 12 April 2000 ДОКУМЕНТ ДЛЯ ПРИНЯТИЯ РЕШЕНИЙ Ф. »
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.
Один треугольник находится внутри другого докажите что его периметр меньше
Задача 1: a, b, c – стороны треугольника. a = 3,17, b = 0,75, c – целое число. Найти c.
Задача 2: Доказать, что в четырехугольнике диагональ меньше половины периметра.
Задача 3:
a) Доказать, что в четырехугольнике любая сторона меньше суммы остальных.
b) То же для любого многоугольника.
Задача 4: Есть 7 прутьев длиннее 9 см, но короче 1 м. Доказать, что из трех из них можно составить треугольник.
Задача 5: Найти точку на данной прямой, сумма расстояний от которой до двух данных точек минимальна.
Решение: Указание: если точки лежат по одну сторону от прямой, отразите одну из них относительно этой прямой.
Задача 6: Найти точку внутри четырехугольнике, сумма расстояний от которой до вершин минимальна.
Решение: Точка пересечения диагоналей
Задача 7: A и B – точки внутри многоугольника. Доказать, что расстояние между ними меньше половины периметра многоугольника.
Задача 8: Доказать, что в выпуклом четырехугольнике сумма диагоналей больше суммы противоположных сторон.
Задача 9: Доказать, что в выпуклом четырехугольнике сумма диагоналей больше полупериметра, но меньше периметра.
Задача 10: Доказать, что в выпуклом n-угольнике (n > 3) не больше двух сторон, которые длиннее любой диагонали.
Задача 11: Один треугольник лежит внутри другого. Доказать, что периметр внутреннего треугольника меньше периметра внешнего
a) если треугольники имеют общую сторону и угол.
b) если треугольники имеют общий угол.
c) если треугольники имеют общую сторону.
Задача 12: Один выпуклый многоугольник лежит внутри другого. Доказать, что периметр у внутреннего многоугольника меньше, чем у внешнего.
Задача 13: Доказать, что перпендикуляр короче наклонной.
Задача 14: В лесу 100 деревьев. Высота любого больше 10, но меньше 40 метров. Расстояние между любыми двумя деревьями не больше разности их высот. Доказать, что лес можно обнести забором длинны 81 метр.
Задача 15: Доказать, что сумма расстояний от точки внутри треугольника до его вершин больше его полупериметра, но меньше периметра.
Задача 16: Доказать, что в выпуклом 5-угольнике сумма диагоналей больше периметра, но меньше удвоенного периметра.
Задача 17: a) Доказать, что из двух наклонных короче та, которая ближе к перпендикуляру.
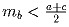
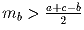
b) В треугольнике ABC точка L лежит на стороне BC. Доказать, что AL b a) , b) .
Решение:
a) Достройте треугольник до параллелограмма
b) Сложите неравенства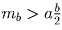 
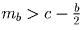
и 
.
Задача 19: Дан угол и точки A и B внутри него. Найти X и Y на сторонах угла такие, что длина пути AXYB минимальна.
Задача 20: На столе лежат несколько разных, но правильно идущих часов. Доказать, что найдется момент, когда сумма расстояний от центра стола до концов минутных стрелок больше суммы расстояний от центра стола до центров часов.
Решение: Это обязательно случится в один из двух моментов, разделённых получасом, так как расстояние до центра каждых часов меньше полусуммы расстояний до конца минутной стрелки, измеренных в эти два момента.
Задача 21: Доказать, что в любом выпуклом 5-угольнике есть три диагонали, из которых можно составить треугольник.
Задача 22: Многоугольник, вырезанный из бумаги, сложили, перегнув по одной линии. Доказать, что в результате этого периметр уменьшился.
Задача 23: Стороны треугольника выражаются целыми числами. Может ли его медиана иметь длину 1?
Один треугольник находится внутри другого докажите что его периметр меньше
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.
Какое отношение это имеет к предыдущей задаче Вот какое: если мы разрешаем углы больше 180, то всё просто | угол в 360 разрезан на 5 равных частей, сумма которых равна 360, и т. д. Если же мы не хотим говорить об углах, больших 180, то это рассуждение не годится и надо действовать чуть сложнее. Проведём какую-нибудь прямую через заданную точку, которая разделит два из пяти углов на части. Всего получится 7 частей. В сумме эти части дают столько же, сколько наши пять углов (каждый разрезанный угол равен сумме двух его частей). С другой стороны, эти части складываются в два развёрнутых угла, поэтому в сумме дают 2 180.
23. Из точки выходят четыре луча, делящие плоскость на четыре угла. При этом оказалось, что (считая против часовой стрелки) первый угол равен третьему, а второй | четвёртому. Докажите, что лучи составляют две прямые (продолжая друг друга).
Обозначим первый и третий углы (они равны) через, а второй и четвёртый | через. Тогда + + + = 360, то есть 2 + 2 = 360, поэтому 2( + ) = 360, и + = 180. А рядом находящиеся углы, в сумме дающие 180, составляют развёрнутый угол.
Ещё несколько задач 24. Имеется деревянный угольник с углом в 19.
Как построить с его помощью угол в 1 Что будет, если откладывать угол в 19, пока не получится полный круг 25. Прямой угол разделен двумя лучами на три угла. Один из них на 10 больше другого и на меньше третьего. Найдите величины углов. [ Ответ:
30, 20, 40.] 26. Прямой угол разделен двумя лучами на три угла. Один из них в два раза меньше другого и в три раза меньше третьего. Найдите величины углов.
[ Ответ: 15, 30, 45.] 27. В полдень минутся и часовая стрелки совпали. Когда они совпадут в следующий раз [ Ответ:
Через 12/11 часа.] 28. Сколько раз в течение суток часовая и минутная стрелки совпадают Сколько раз они образуют развёрнутый угол прямой угол 29. Через точку на плоскости провели 10 прямых, после чего плоскость разрезали по этим прямым на углы. Докажите, что хотя бы один из этих углов меньше 20. Всего 20 лучей, 20 углов по дают 400 > 360.
30. Из одной точки выходят четыре луча. (перечисленные по часовой стрелке), которые делят плоскость на четыре угла, три из которых таковы: = 45, = 90, = 105. Найдите четвёртый угол. Найдите углы и. [ Ответ: 120, 135, (если брать угол, меньший 180; если складывать и, то получится угол в 195, больший развёрнутого).] 31. Из одной точки проведены три луча, и. Известно, что = 10, = 20.
Чему может быть равен угол Укажите все возможности. [ Ответ: 10, 30.] 32. Из одной точки проведены четыре луча,, и. Известно, что = 10, = 20 = 40. Чему может быть равен угол Укажите все возможности. [ Ответ: 10, 30, 50, 70.] 33. Угол равен 100. Луч проведён так, что угол на 10 больше угла. Чему равны углы и (Укажите все возможности.) [ Ответ: 55, 45; другой вариант | 135, 125.] 34. Угол равен 100. Луч проведён так, что угол в полтора раза больше угла. Чему равны углы и (Укажите все возможности.) [ Ответ: 60, 40; другой вариант | 156, 104.] 35. Из точки провели четыре луча, делящих плоскость на четыре угла, которые пронумеровали по часовой стрелке. Докажите, что если первый и третий углы равны, то биссектрисы второго и четвёртого лежат на одной прямой.
36. Из точки на листе бумаги провели четыре луча, делящих плоскость на четыре угла. Затем лист разрезали по биссектрисам этих углов на четыре части (которые тоже являются углами). Докажите, что два из этих углов образуют в сумме 180, и два остальных | тоже.
37. Прямой угол разделён на два. Найдите угол между биссектрисами получившихся углов.
38. Из бумаги вырезано много одинаковых углов, величина которых составляет целое число градусов.
Известно, что 21 такой угол можно приложить друг к другу, и они ещё не заполнят всей плоскости, а 22 уже не поместятся. Найдите величину углов.
[ Ответ: 360/21 > > 360/22; = 17.] 39. Можно ли нарисовать треугольник и точку внутри него, из которой любая сторона видна под прямым углом 3 90 = 270
46. Расстояние равно 5, а расстояние равно 3. Может ли расстояние быть равно 9 Может ли расстояние быть равно 1 На оба вопроса ответ отрицательный. В первом случае это невозможно, так как не может быть больше + = 5 + 3 = 8. Во втором случае дело немного сложнее, и надо применить неравенство треугольника к тем же точкам в другом порядке. Если = 1, то получится, что + = 3 + 1 = 4; между тем = 5. Получается, что > +, чего не может быть (неравенство треугольника, только точки переименованы).
47. На плоскости даны четыре точки,, и. Докажите, что + +.
Это неравенство можно было бы называть неравенст вом четырёхугольника и прочесть так: сторона четырёхугольника не меньше суммы трёх других его сторон. (Или так: ломаный путь не короче прямого.) Оно является следствием неравенства треугольника, и чтобы увидеть это, достаточно провести в четырёхугольнике диагональ. В самом деле, если в сумме + + заменить два первых слагаемых на, то по неравенству треугольника сумма уменьшится (или останется той же, если точка лежит на отрезке ). Остаётся второй раз применить неравенство треугольника и заметить, что +.
Повторим наше рассуждение более формально. По неравенству треугольника, +. Прибавляя к обеим частям, видим, что + + +. С другой стороны, по неравенству треугольника +.
48. Докажите, что в треугольнике любая сторона меньше половины периметра (суммы сторон).
53. Докажите, что длина ломаной линии (непрерывной линии, составленой из нескольких отрезков) не меньше расстояния между её концами. (Таким образом, прямой путь всегда короче непрямого.) Будем спрямлять наш путь постепенно. Возьмём какой-то участок пути из двух звеньев и и заменим участок < < на отрезок <.
По неравенству треугольника путь сократится, а количество звеньев ломаной уменьшится на 1. После нескольких таких сокращений мы и получим прямой путь.
54. Многоугольник разрезали по прямой на две части. Докажите, что периметр каждой из частей меньше периметра исходного многоугольника. (Другими словами, если отрезать от бумажного многоугольника кусок, сделав прямой разрез, то его периметр уменьшится.) Периметр каждой из частей отличается от полного периметра исходного многоугольника тем, что ломаный участок пути заменён на прямой. От этого периметр может только уменьшиться.
Эта задача требует некоторого пояснения. Вообще говоря, прямая может делить многоугольник не на две части, а на три или даже больше (см. рисунок). Такие многоугольники называют невып уклыми. Но и в этом случае периметр каждой части (по тем же причинам) не больше периметра исходного многоугольника.
Можно по-разному объяснять, что такое выпуклый многоугольник. Вот несколько вариантов:
многоугольник выпуклый, если • всякий отрезок, соединяющий две точки внутри многоугольника, целиком лежит в нём;
• многоугольник лежит по одну сторону от любой прямой, проведённой по его стороне;
• все углы в нём меньше 180;
• его можно вырезать из бумаги, разрезая её по прямым.
Интуитивно ясно, что все эти свойства описывают одни и те же многоугольники (как говорят математики, экви валентны ), но строго доказать это (и даже сформулировать) совсем не просто.
55. Один выпуклый многоугольник лежит внутри другого. Докажите, что периметр внутреннего многоугольника меньше периметра внешнего.
Внутренний многоугольник можно вырезать из внешнего, проводя разрезы по сторонам. Каждый из таких разрезов отрезает от остающегося многоугольника кусок и (как мы видели в задаче 54) уменьшает периметр, пока в итоге не получится внутренний многоугольник.
Ещё несколько задач 56. Может ли в треугольнике сторона быть вдвое больше другой стороны и вдвое меньше третьей [ Ответ: /2 + Pages: | 1 |
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.