какая асимптотическая сложность бинарного поиска в отсортированном массиве размера n

Оценка сложности алгоритмов, или Что такое О(log n)

Авторизуйтесь

Оценка сложности алгоритмов, или Что такое О(log n)

Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.

Оценка сложности

Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.

Примеры

O(n) — линейная сложность

Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.

O(log n) — логарифмическая сложность

Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.

O(n 2 ) — квадратичная сложность

Старт 4 ноября, 9 месяцев, Онлайн, Беcплатно

Бывают и другие оценки по сложности, но все они основаны на том же принципе.

Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.

Наглядно

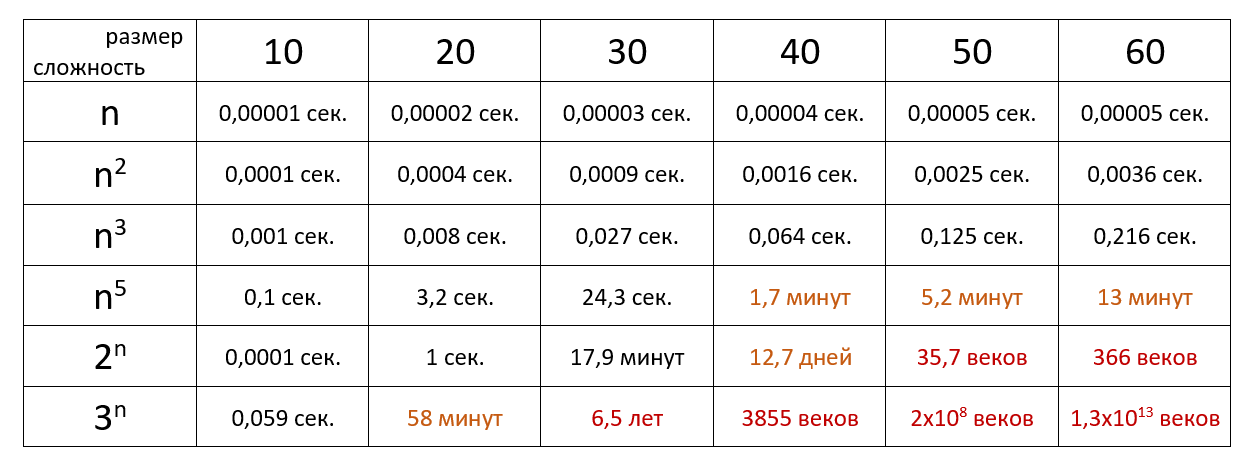
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:

Тут можно посмотреть сложность основных алгоритмов сортировки и работы с данными.

Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».

Источник

Введение в анализ сложности алгоритмов (часть 3)

От переводчика: данный текст даётся с незначительными сокращениями по причине местами излишней «разжёванности» материала. Автор абсолютно справедливо предупреждает, что отдельные темы могут показаться читателю чересчур простыми или общеизвестными. Тем не менее, лично мне этот текст помог упорядочить имеющиеся знания по анализу сложности алгоритмов. Надеюсь, что он окажется полезен и кому-то ещё.
Из-за большого объёма оригинальной статьи я разбила её на части, которых в общей сложности будет четыре.
Я (как всегда) буду крайне признательна за любые замечания в личку по улучшению качества перевода.

Логарифмы

Практическая рекомендация: на соревнованиях алгоритмы часто реализуются на С++. Как только вы проанализировали сложность вашего алгоритма, так сразу можете получить и грубую оценку того, как быстро он будет работать, приняв, что в секунду выполняется 1 000 000 команд. Их количество считается из полученной вами функции асимптотической оценки, описывающей алгоритм. Например, вычисление по алгоритму с Θ( n ) займёт около секунды при n = 1 000 000.

Рекурсивная сложность

Если вы всё же не уверены в этом, то вы всегда можете найти точную сложность путём подсчёта количества инструкций. Примените этот метод к данной функции, чтобы найти её f( n ), и убедитесь, что она линейная (напомню, что линейность означает Θ( n ) ).

Логарифмическая сложность

Одной из известнейших задач в информатике является поиск значения в массиве. Мы уже решали её ранее для общего случая. Задача становится интереснее, если у нас есть отсортированный массив, в котором мы хотим найти заданное значение. Одним из способов сделать это является бинарный поиск. Мы берём средний элемент из нашего массива: если он совпадает с тем, что мы искали, то задача решена. В противном случае, если заданное значение больше этого элемента, то мы знаем, что оно должно лежать в правой части массива. А если меньше — то в левой. Мы будем разбивать эти подмассивы до тех пор, пока не получим искомое.

Вот реализация такого метода в псевдокоде:

Если вы не уверены, что метод работает в принципе, то отвлекитесь и решите вручную какой-нибудь простой пример.

Если вы прочли раздел о логарифмах выше, то такое выражение будет для вас знакомым. Решив его, мы получим:

Практическая рекомендация: улучшение асимптотического времени выполнения программы часто чрезвычайно повышает её производительность. Намного сильнее, чем небольшая «техническая» оптимизация в виде использования более быстрого языка программирования.

Источник

Асимптотическая нотация

Измерить скорость алгоритма реальным временем — секундами и минутами — непросто. Одна программа может работать медленнее другой не из-за собственной неэффективности, а по причине медлительности операционной системы, несовместимости с оборудованием, занятости памяти компьютера другими процессами…

Для измерения эффективности алгоритмов придумали универсальные концепции, и они выдают результат независимо от среды, в которой запущена программа. Измерение асимптотической сложности задачи производится с помощью нотации О-большого.

Вот формальное определение:

Не бойтесь формального определения! По сути, оно определяет асимптотическое возрастание времени работы программы, когда количество ваших данных на входе растет в сторону бесконечности. Например, вы сравниваете сортировку массива из 1000 элементов и 10 элементов, и нужно понять, как возрастёт при этом время работы программы. Или нужно подсчитать длину строки символов путем посимвольного прохода и прибавлением 1 за каждый символ:

Представьте, что в переменной length вы сохранили значение, равное количеству символов в строке. Например, length = 1000. Чтобы получить длину строки, нужен только доступ к этой переменной, на саму строку можно даже не смотреть. И как бы мы ни меняли длину, мы всегда можем обратиться к этой переменной. В таком случае асимптотическая скорость = O(1). От изменения входных данных скорость работы в такой задаче не меняется, поиск завершается за постоянное время. В таком случае программа является асимптотически постоянной.

Недостаток: вы тратите память компьютера на хранение дополнительной переменной и дополнительное время для обновления её значения.

Но в какой-то момент квадратичная функция обгонит линейную, от этого не уйти.

В случае бинарного поиска = Ω(1) (находит за постоянное время независимо от размера массива).

Источник

Асимптотическая сложность алгоритмов: что за зверь?

Асимптотическая сложность алгоритмов встречается повсеместно. Доступно рассказываем, что это такое, где и как используется.

Асимптотическая сложность алгоритмов представляет собой время и память, которые понадобятся вашей программе в процессе экзекуции. Одно дело – знать, что существуют линейные или логарифмические алгоритмы, но совсем другое – понимать, что же за всем этим стоит.

С помощью Big O Notation можно математически описать то, как поведет себя программа в условиях наихудшего сценария при большом количестве входных данных. Например, если вы используете сортировку пузырьком, чтобы отсортировать элементы в целочисленном массиве по возрастанию, то худшим сценарием в этом случае будет отсортированный в убывающем порядке массив. При таком раскладе вашему алгоритму понадобится наибольшее количество операций и памяти.

Разобравшись в принципе работы Big O Notation, вы сможете решить проблему оптимизации ваших программ и добиться максимально эффективного кода.

Сложности О(1) и O(n) самые простые для понимания.

О(1) означает, что данной операции требуется константное время. Например, за константное время выполняется поиск элемента в хэш-таблице, так как вы напрямую запрашиваете какой-то элемент, не делая никаких сравнений. То же самое относится к вызову i-того элемента в массиве. Такие операции не зависят от количества входных данных.

Например, если у вас есть отсортированный массив, насчитывающий 8 элементов, в худшем случае вам понадобится сделать Log_2(8)=3 сравнений, чтобы найти нужный элемент.

Рассмотрим отсортированный одномерный массив с 16 элементами:

Допустим, нам нужно найти число 13.

Мы выбираем медиану массива и сравниваем элемент под индексом 7 с числом 13.

Так как наш массив отсортирован, а 16 больше, чем 13, мы можем не рассматривать элементы, которые находятся под индексом 7 и выше. Так мы избавились от половины массива.

Дальше снова выбираем медиану в оставшейся половине массива.

Сравниваем и получаем, что 8 меньше, чем 13. Уменьшаем массив вдвое, выбираем элемент посередине и делаем еще одно сравнение. Повторяем процесс, пока не останется один элемент в массиве. Последнее сравнение возвращает нужный элемент. Лучшее развитие событий – если первая выбранная медиана и есть ваше число. Но в худшем случае вы совершите log_2(n) сравнений.

То же самое произойдет, если вам надо будет пройтись по элементам двумерного массива.

Использование алгоритмов, которые работают в O(n^2) и выше (например, экспоненциальная функция 2^n ), является плохой практикой. Следует избегать подобных алгоритмов, если хотите, чтобы ваша программа работала за приемлемое время и занимала оптимальное количество памяти.

Источник

как рассчитать сложность бинарного поиска

Я слышал, как кто-то сказал, что поскольку бинарный поиск делит пополам входные данные, необходимые для поиска, то это алгоритм log (n). Так как я не имею математического образования, я не могу иметь к нему отношение. Может кто-нибудь объяснить это немного подробнее? это имеет отношение к логарифмической серии?

Здесь более математический способ увидеть это, хотя и не очень сложно. ИМО намного понятнее, чем неформальные:

Вопрос в том, сколько раз вы можете разделить N на 2, пока не получите 1? По сути, это говорит о том, что бинарный поиск (половина элементов), пока вы не нашли его. В формуле это будет так:

Теперь сделайте журнал ₂ :

это означает, что вы можете разделить журнал N раз, пока у вас все не будет разделено. Это означает, что вы должны делить log N («выполнить бинарный поиск»), пока не найдете свой элемент.

Для двоичного поиска T (N) = T (N / 2) + O (1) // рекуррентное соотношение

Применить теорему Мастера для вычисления сложности времени выполнения рекуррентных соотношений: T (N) = aT (N / b) + f (N)

Здесь a = 1, b = 2 => log (база b) = 1

также здесь f (N) = n ^ c log ^ k (n) // k = 0 & c = log (основание b)

Итак, T (N) = O (N ^ c log ^ (k + 1) N) = O (log (N))

T (n / 2) = T (n / 4) + 1 + 1

Как мы взяли 2 ^ k = n

Таким образом, сложность Времени O (log n)

Это не половина времени поиска, это не сделало бы это log (n). Это уменьшает это логарифмически. Задумайтесь об этом на мгновение. Если у вас 128 записей в таблице и вам нужно искать значение линейно, то, вероятно, потребуется около 64 записей в среднем, чтобы найти ваше значение. Это н / 2 или линейное время. При бинарном поиске вы устраняете 1/2 возможных записей на каждой итерации, так что самое большее потребуется всего 7 сравнений, чтобы найти ваше значение (логарифмическая база 2 из 128 равна 7 или 2, а степень 7 равна 128). сила бинарного поиска.

2,85. Log2 (7) составляет

2,81. У меня нет математического фона, чтобы объяснить разницу в 0,04, но я думаю, что это связано с отсутствием дробных битов или какой-то другой магией 🙂

Это просто формальный математический жаргон для того, чтобы иметь возможность доказывать утверждения и т. Д. Он имеет очень простое объяснение. Когда n становится очень большим, функция log n будет увеличивать время, необходимое для выполнения функции. Размер «входного набора», n, это просто длина списка.

Проще говоря, причина бинарного поиска в O (log n) состоит в том, что он вдвое сокращает входной набор в каждой итерации. Проще думать об этом в обратной ситуации. На x итерациях, какой длинный список может проверить алгоритм двоичного поиска в max? Ответ 2 ^ х. Отсюда видно, что наоборот, в среднем алгоритму двоичного поиска требуется log2 n итераций для списка длины n.

Если вы посмотрите на простой итеративный подход. Вы просто удаляете половину элементов для поиска, пока не найдете нужный элемент.

Вот объяснение того, как мы придумали формулу.

Так что худший случай будет

Это показывает худший случай, когда вы достигаете N / 2 x, где x таков, что 2 x = N

В других случаях N / 2 x, где x таков, что 2 x x = N
=> log ₂ (2 x ) = log ₂ (N)
=> x * log ₂ (2) = log ₂ (N)
=> x * 1 = log ₂ (N)
=> Более формально ⌊log ₂ (N) + 1⌋

Источник