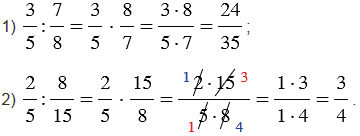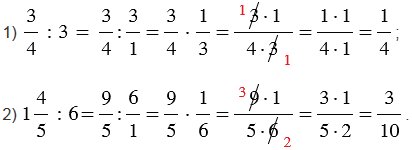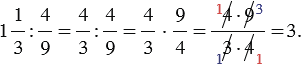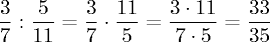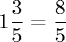кака разделить дробь на дробь
Деление дробей: теория и практика
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.
Основные свойства дроби
1. Дробь не имеет значения, при условии, если делитель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Две дроби a/b и c/d называются равными, если a * d = b * c.
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Деление дробных чисел
Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.
Свойства деления:
1. При делении на единицу получится такое же число:
2. На ноль делить нельзя.
3. Когда делим ноль на любое число, всегда получаем ноль:
4. Когда делим любое число на само себя получаем единичку:
5. Когда делим сумму на какое-либо число, можно разделить на него каждое слагаемое, а потом сложить полученное:
6. Когда делим разность на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе:
7. Когда делим произведение двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель:
Записывайся на онлайн обучение по математике, с лучшими учителями! Для учеников с 1 по 11 классы!
Деление обыкновенных дробей
Как делить дробь на дробь? Выполняем следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам неважно, одинаковые знаменатели или нет.
Деление дроби на натуральное число
Для деления дроби на натуральное число нужно:
Деление натурального числа на дробь
Чтобы поделить натуральное число на обыкновенную дробь нужно:
Деление на смешанное число
Для деления смешанных чисел необходимо:
Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Деление обыкновенных дробей
Примеры:
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Деление смешанных чисел
| Чтобы выполнить деление смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом деления дробей. |
Примеры:
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Деление на натуральное число
При делении дроби на натуральное число, учитываем то, что любое натуральное число можно представить в виде дроби со знаменателем 1, затем пользуемся правилом деления дробей.
Примеры:
Обратите внимание, если возможно, то прежде, чем перемножить числа, выполняем сокращение (такой ход действий облегчит вычисления).
Нахождения числа по его дроби
| Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь |
Примеры:
1) Найдите число, если 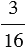
2) Найдите число, если 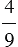
Поделись с друзьями в социальных сетях:
Деление обыкновенных дробей: правила, примеры, решения
С дробями можно выполнять все действия, в том числе и деление. Данная статья показывает деление обыкновенных дробей. Будут даны определения, рассмотрены примеры. Подробно остановимся на делении дробей на натуральные числа и наоборот. Будет рассмотрено деление обыкновенной дроби на смешанное число.
Деление обыкновенных дробей
Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.
Отсюда получим и сформулируем правило деления обыкновенных дробей:
Запишем правило в виде выражения: a b : c d = a b · d c
Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.
Перейдем к рассмотрению деления обыкновенных дробей.
Ответ: 9 7 : 5 3 = 27 35 .
При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.
Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 8 15 : 24 65 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Необходимо произвести сокращение, а это выполняется следующим образом: 8 · 65 15 · 24 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Деление необыкновенной дроби на натуральное число
Рассмотрим данное деление дроби на число.
Решение
Ответ: 16 45 : 12 = 4 135 .
Деление натурального числа на обыкновенную дробь
Ответ: 25 : 15 28 = 46 2 3 .
Деление обыкновенной дроби на смешанное число
При делении обыкновенной дроби на смешанное число легко можно свети к делению обыкновенных дробей. Нужно совершить перевод смешанного числа в неправильную дробь.
Деление смешанного числа производится таким же образом, как и обыкновенных.
Как разделить дробь на дробь
Для того, чтобы разделить обыкновенную дробь на обыкновенную дробь, нужно умножить первую дробь на «перевернутую» вторую дробь. Такая «перевернутая» обыкновенная дробь, где числитель и знаменатель поменяли местами называется обратной.
При делении дробей необходимо обратить внимание на то, чтобы вторая дробь не равнялась нулю. Иногда, если дробь имеет довольно-таки громоздкий вид, это сделать весьма затруднительно. Кроме того, вторая дробь может содержать некоторые переменные (неизвестные) величины, которые при определенных значениях обращают дробь в нуль. Также нужно уделить внимание тем случаям, когда знаменатель второй дроби обращается в нуль. При действиях с переменными все эти случаи необходимо указать в окончательном ответе.
Чтобы разделить смешанную дробь на смешанную, смешанную дробь на обыкновенную или обыкновенную на смешанную, нужно привести смешанные дроби к обыкновенному виду. После чего произвести деление, как указано в шаге 1.
Для перевода смешанной дроби к обыкновенной необходимо целую часть смешанной дроби умножить на ее знаменатель и прибавить полученное произведение к числителю.
При делении десятичной дроби на обыкновенную (смешанную) или при делении обыкновенной (смешанной) дроби на десятичную, все дроби приводятся к обыкновенному виду. После этого деление производится согласно шагу 1. Для перевода десятичной дроби в обыкновенную, «выкидываем» из десятичной дроби запятую и записываем в числитель дроби, а в знаменатель пишем единицу и столько нулей, сколько цифр стояло справа от десятичной точки.
Для деления двух десятичных дробей нужно в делимом и делителе перенести десятичную точку на столько цифр вправо, чтобы из второй дроби получилось целое число и разделить полученные числа.
Если при этом в делимом для переноса десятичной запятой «не хватает» цифр, то недостающие знаки заменяются нулями.
Дроби. Умножение и деление дробей.
Умножение обыкновенной дроби на дробь.
Чтобы перемножить обыкновенные дроби, необходимо умножить числитель на числитель (получим числитель произведения) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби. Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Обратите внимание! Здесь не нужно искать общий знаменатель!!
Деление обыкновенной дроби на дробь.
Деление обыкновенной дроби на дробь происходит так: переворачиваете вторую дробь (т.е. меняете числитель и знаменатель местами) и после этого дроби перемножаются.
Формула деления обыкновенных дробей:
Умножение дроби на натуральное число.
Обратите внимание! При умножении дроби на натуральное число, числитель дроби умножается на наше натуральное число, а знаменатель дроби оставляем прежним. Если результатом произведения оказалась неправильная дробь, то обязательно выделите целую часть, превратив неправильную дробь в смешанную.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением, переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.