как вы думаете какая теория может объяснить различное поведение двух братьев близнецов

Мнимые парадоксы СТО. Парадокс близнецов

Парадокс близнецов, он же парадокс Ланжевена, он же парадокс часов – это первый и наиболее известный парадокс СТО, основанный на тезисе, сформулированном Эйнштейном в основополагающей работе «К электродинамике движущихся тел». Статус «парадокса» появился позднее. В предлагаемой работе показано, что задача о близнецах не является парадоксом, это рядовая задача специальной теории относительности, имеющая в ней однозначное, непротиворечивое решение.

Тем не менее, в литературе и в интернете до сих пор идут многочисленные дискуссии по этому парадоксу. Предложено и вновь предлагаются множество его решений (объяснений), из которых делаются выводы как о непогрешимости СТО, так и её ложности. Впервые тезис, послуживший основой для формулировки парадокса, был изложен Эйнштейном в его основополагающей работе по специальной (частной) теории относительности «К электродинамике движущихся тел» в 1905 году:

«Если в точке А находятся двое синхронно идущих часов и мы перемещаем одни из них по замкнутой кривой с постоянной скоростью до тех пор, пока они не вернутся в А (. ), то эти часы по прибытии в А будут отставать по сравнению с часами, остававшимися неподвижными. ».

В дальнейшем этот тезис получил собственные имена «парадокс часов», «парадокс Ланжевена» и «парадокс близнецов». Последнее название прижилось, и в настоящее время чаще встречается формулировка не с часами, а с близнецами и космическими полётами: если один из близнецов улетает на космическом корабле к звёздам, то по возвращению он оказывается моложе своего остававшегося на Земле брата.

Парадокс, кажущееся противоречие в предсказаниях теории относительности возникает, если движущимся близнецом считать того, который оставался на Земле. В этом случае теперь уже улетавший в космос близнец должен ожидать, что остававшийся на Земле брат окажется моложе него. Так же и с часами: с точки зрения часов на экваторе движущимися следует считать часы на полюсе. Таким образом, и возникает противоречие: так кто же из близнецов окажется моложе? Какие из часов покажут время с отставанием?

Чаще всего парадоксу обычно даётся простое объяснение: две рассматриваемые системы отсчета на самом деле не являются равноправными. Близнец, который улетал в космос, в своём полёте не всегда находился в инерциальной системе отсчета, в эти моменты он не может использовать уравнения Лоренца. Так же и с часами.

Отсюда следует сделать вывод: в СТО не может быть корректно сформулирован «парадокс часов», специальная теория не делает двух взаимоисключающих предсказаний. Полное решение задача получила после создания общей теории относительности, которая решила задачу точно и показала, что, действительно, в описанных случаях отстают движущиеся часы: часы улетавшего близнеца и часы на экваторе [2]. «Парадокс близнецов» и часов, таким образом, является рядовой задачей теории относительности.

Вариации на тему «парадокса близнецов»

Гораздо реже обсуждается другой, сформулированный Эйнштейном в этой же работе и следующий сразу же за первым, тезис об отставании часов на экваторе от часов, находящихся на полюсе Земли. Смыслы обоих тезисов совпадают:

«… часы с балансиром, находящиеся на земном экваторе, должны идти несколько медленнее, чем точно такие же часы, помещённые на полюсе, но в остальном поставленные в одинаковые условия».

На первый взгляд это утверждение может показаться странным, ведь расстояние между часами неизменно и нет относительной скорости между ними. Но на самом деле на изменение темпа хода часов влияет мгновенная скорость, которая, хотя и меняет непрерывно своё направление (тангенциальная скорость экватора), но все в сумме они дают ожидаемое отставание часов.

Недоумение развеется, если добавить третьи часы вблизи траектории движущихся часов и идущие синхронно с часами в центре (на полюсе). Относительно третьих часов движущиеся часы имеют бесспорное относительное движение и, следовательно, замедление темпа хода. Но часы в центре и вне окружности идут синхронно, поэтому движущиеся часы замедляют ход и по отношению к часам в центре.

X^2 + y^2 = R^2
где,
x, y – координаты движущихся часов Т2 в системе отсчета неподвижных;
R – радиус окружности, описываемой движущимися часами Т2.

Очевидно, что с точки зрения движущихся часов Т2, расстояние между ними и неподвижными часами Т1 также равно R в любой момент времени. Но известно, что геометрическим местом точек, равно удалённых от заданной, является окружность. Следовательно, и в системе отсчета движущихся часов Т2, неподвижные часы Т1 движутся вокруг них по окружности:

x1^2 + y1^2 = R^2
где,
x1, y1 – координаты неподвижных часов Т1 в системе отсчета движущихся;
R – радиус окружности, описываемой неподвижными часами Т1.

А это, в свою очередь, означает, что с точки зрения специальной теории относительности и в этом случае должно возникнуть отставание часов. Очевидно, что в этом случае, наоборот: Т2 > T3 = T. Получается, что и на самом деле специальная теория относительности делает два взаимоисключающих предсказания Т2 > T3 и Т2 < T3?

И это действительно так, если не принять во внимание, что теория была создана для инерциальных систем отсчета. Здесь же движущиеся часы Т2 не находятся в инерциальной системе. Само по себе это не запрет, а лишь указание на необходимость учесть это обстоятельство. И это обстоятельство разъясняет общая теория относительности [2].

Применять его или нет, можно определить простым опытом. В инерциальной системе отсчета на тела не действуют никакие внешние силы. В неинерциальной системе и согласно принципу эквивалентности общей теории относительности на все тела действует сила инерции или тяготения. Следовательно, маятник в ней отклонится, все незакреплённые тела будут стремиться переместиться в одном направлении.

Такой опыт рядом с неподвижными часами Т1 даст отрицательный результат, будет наблюдаться невесомость. А вот рядом с движущимися по окружности часами Т2 на все тела будет действовать сила, стремящаяся отбросить их от неподвижных часов. Мы, разумеется, считаем, что никаких иных гравитирующих тел поблизости нет. Кроме того, движущиеся по окружности часы Т2 сами по себе не вращаются, то есть, движутся не так, как Луна вокруг Земли, обращённая к ней всегда одной и той же стороной. Наблюдатели рядом с часами Т1 и Т2 в своих системах отсчета будут видеть удалённый от них на бесконечность объект всегда под одним и тем же углом.

Таким образом, движущийся с часами Т2 наблюдатель должен учесть факт неинерциальности своей системы отсчета в соответствии с положениями общей теории относительности. Эти положения говорят, что часы в поле гравитации или в эквивалентном ему поле инерции, замедляют свой ход. Поэтому в отношении неподвижных (по условиям опыта) часов Т1 он должен признать, что эти часы находятся в гравитационном поле меньшей напряженности, поэтому они идут быстрее его собственных и к их ожидаемым показаниям следует добавить гравитационную поправку.

Напротив, наблюдатель рядом с неподвижными часами Т1 констатирует, что движущиеся часы Т2 находятся в поле инерционной гравитации, поэтому идут медленнее и от их ожидаемых показаний следует отнять гравитационную поправку.

Как видим, мнение обоих наблюдателей полностью совпали в том, что движущиеся в исходном смысле часы Т2 отстанут. Следовательно, специальная теория относительности в «расширенной» трактовке делает два строго согласованных предсказания, что не даёт никаких оснований для провозглашения парадоксов. Это рядовая задача, имеющая вполне конкретное решение. Парадокс в СТО возникает лишь в том случае, если использовать её положения к объекту, не являющимся объектом специальной теории относительности. Но, как известно, неверная посылка может привести как к правильному, так и к ложному результату.

Эксперимент, подтверждающий СТО

Следует отметить, что все эти рассмотренные мнимые парадоксы соответствуют мысленным экспериментам на основе математической модели под названием Специальная Теория Относительности. То, что в этой модели данные эксперименты имеют полученные выше решения, не обязательно означает, что в реальном физическом эксперименты будут получены такие же результаты. Математическая модель теории прошла многолетнее испытание и в ней не найдено никаких противоречий. Это значит, что все логически корректные мысленные эксперименты неизбежно будут давать результат, подтверждающий её [1].

В этой связи представляет особый интерес эксперимент, который общепризнанно в реальных условиях показал точно такой же результат, что и рассмотренный мысленный эксперимент. Непосредственно это означает, что математическая модель теории верно отражает, описывает реальные физические процессы.

Это был первый эксперимент по проверке отставания движущихся часов, известный как эксперимент Хафеле – Китинга, проведённый в 1971 г [3]. Четверо часов, сделанных на основе цезиевых стандартов частоты, были помещены на два самолета и совершили кругосветное путешествие. Одни часы путешествовали в восточном направлении, другие обогнули Землю в западном направлении. Разница в скорости хода времени возникала из-за добавочной скорости вращения Земли, при этом учитывалось и влияние поля тяготения на полетной высоте по сравнению с уровнем Земли. В результате эксперимента удалось подтвердить общую теорию относительности, измерить различие в скорости хода часов на борту двух самолетов. Полученные результаты были опубликованы в журнале Science в 1972 году.

Источник

Парадокс близнецов

Парадокс близнецов (RA050) — одна из наиболее известных попыток демонстрации противоречивости специальной теории относительности. В основу кажущегося противоречия положена относительность релятивистского замедления времени, которое должно наблюдаться в системах отсчёта, движущихся относительно наблюдателя (детальнее — см. формулировку ниже).

В виде парадокса данный эффект впервые был сформулирован Полем Ланжевеном в 1911 году, и на протяжении десятилетия «парадоксу» были даны несколько объяснений с применением разных методов теории относительности (в т.ч. самим Эйнштейном, который объяснил его на основании своей теории гравитации). Позднее, в конце 1950-х, работы Герберта Дингла породили новый всплеск внимания к «парадоксу», и в них были оспорены существующие его объяснения. Многими учёными эта критика была признана несостоятельной, и в настоящее время, несмотря на иногда появляющиеся публикации о «парадоксе» как о демонстрации противоречивости ТО, большинство учёных считает «парадокс» разрешённым.

Содержание

Формулировка [ править ]

Одна из возможных формулировок парадокса такова.

Из двух братьев-близнецов один отправляется в межзвёздное путешествие («путешественник») на субсветовой скорости до звезды, расстояние до которой составляет (например) 5 световых лет, а второй остаётся ожидать на Земле («домосед»). Полагается, что путешественник и домосед пребывают в одинаковом взаимном положении, и далее следуют противоречивые выводы, «опровергающие» ТО:

Источник [ править ]

Хайдаров К.А. Галактическая эволюция [1] (в книге «парадокс» преподносится в качестве опровержения ТО).

Разъяснение [ править ]

Неравноправность систем отсчёта [ править ]

Как это и предполагается в формулировке парадокса, система отсчёта, связанная с Землёй, будет считаться инерциальной с приемлемой для данной задачи точностью. Вместе с тем, движение звездолёта, ускоряющегося до субсветовой скорости, инерциальной системой отсчёта считать нельзя. Следовательно, путешественник и домосед не оказываются в равных условиях: лишь последний пребывает в инерциальной системе отсчёта.

Согласно первому постулату теории относительности (принципу относительности), все инерциальные системы отсчёта равноправны. Это означает, что нет опытов, позволяющих установить различие между такими системами отсчёта (т.е., все опыты в таких системах будут проходить одинаково). Поскольку путешественник не пребывает в таковой (он испытывает ускорение), то к его системе отсчёта и системе отсчёта домоседа невозможно напрямую применить принцип относительности.

Кроме того, даже если отвлечься от ускорений (предположить что изменения скорости происходят мгновенно), то звездолёт всё равно оказывается в неравных условиях с Землей, т.к. он по крайней мере один раз «меняет» инерциальную систему отсчёта, когда поворачивает обратно. В то время Земля всегда находится в одной и той же ИСО. И именно эта асимметрия приводит к тому, что близнец на звездолёте оказывается моложе близнеца на Земле. Причём эта асимметрия принципиально неустранима: нельзя вернутся в точку старта не изменяя направления вектора скорости.

Подробное решение [ править ]

Переформулировка [ править ]

Рассмотрим ускоренное движение звездолёта, ограничиваясь в рассуждениях специальной теорией относительности.

Прежде всего, необходимо отметить два важных момента, позволяющих сократить изложение:

Следует отметить, что последнее допущение может привести к тому, что время полёта (с точки зрения каждого из наблюдателей) может сократиться, поскольку путешественник теперь не тратит время на ускорение. Вместе с тем, можно показать, что порядок разности показаний часов при достаточно высокой скорости полёта будет тем же.

Решение на основе СТО [ править ]

Пусть — скорость звездолёта, , . Ей соответствует коэффициент (Лоренц-фактор)

определяющий то, во сколько раз с точки зрения «недвижимого» наблюдателя сократится в направлении движения звездолёт, и то, во сколько раз медленнее будет там протекать время.

Теория относительности не налагает ограничения на ускорения, поэтому для простоты можно допустить, что замедление звездолёта происходит достаточно быстро, и его влиянием на ход часов можно пренебречь, а основное время звездолёт проводит в равномерном прямолинейном движении. Следует отметить, что ускорение само по себе не приводит к замедлению времени, но оно приводит к появлению скорости, которая затем оказывает влияние на ход часов. Так, если зведолёт на некотором пути двигался неравномерно, то для определения замедления его собственного времени (относительно времени «неподвижной» системы отсчёта), можно разбить время пути на короткие интервалы, положив, что на каждом из них движение равномерно, и сделав переход к соответствующему интегралу.

Рассмотрим движение с точки зрения домоседа. Допустим, он расценит, что звездолёт потратил лет, двигаясь в одну сторону, и по его измерениям на звездолёте пройдёт примерно лет, что довольно немного.

Путешественник, пролетая через Землю, будет полагать, что до звезды не так далеко: всего-то каких-нибуть световых лет, поскольку пространство вокруг него сжалось вдоль направления его движения (Земля в его системе отсчёта также не будет шарообразной, хотя и она будет казаться таковой визуально). Спустя примерно лет он делает остановку, и сверяет часы. Но он также обнаружит, что его часы отстали.

Дело в том, что если на всём пути звездолёта разместить синхронизированные часы с Землёй, то эти часы уже не будут казаться синхронизированными с точки зрения путешественника: здесь сказывается относительность одновременности, проявляющееся в теории относительности. Хотя каждые отдельно взятые часы с точки зрения путешественника будут идти медленно, но показывать они будут разное время, и это время будет опережать собственное время путешественника примерно в раз. Такое соотношение будет примерно сохраняться до конца полёта.

Теперь же, если звездолёт также быстро (почти мгновенно) разгонится до субсветовой скорости обратно к Земле, то на обратный путь он потратит по собственным часам всё те же лет, а для домоседа пройдёт всё те же лет.

При этом надо отметить, что свет, т.е. изображение Земли, которое путешественник видит в телескоп, так «прыгать» не будет, т.к. свет существует локально, а локальные окрестности в момент разворота меняться не будут.

Итого в момент, когда звездолёт будет пролетать обратно мимо Земли для домоседа проходит суммарно 10 лет, а для космонавта лет и 10 лет для «землянина». Суммарная разница в возрасте составит лет. И эта разница будет объективна и инвариантна: не будет не зависит от выбора системы отсчёта в которой мы наблюдаем за экспериментом.

Т.е. нет никакого противоречия, никакого парадокса в логическом смысле. А есть наблюдаемый физический эффект, который неожидан для обывателя.

Вариации [ править ]

У парадокса близнецов есть множество вариаций, которые пытаются как-то обойти особенности «классического парадокса». В частности:

Источник

Парадокс близнецов

Парадо́кс близнецо́в — мысленный эксперимент, при помощи которого пытаются «доказать» противоречивость специальной теории относительности. Согласно СТО, с точки зрения «неподвижных» наблюдателей все процессы у двигающихся объектов замедляются. С другой стороны, принцип относительности декларирует равноправие инерциальных систем отсчёта. На основании этого строится рассуждение, приводящее к кажущемуся противоречию. Для наглядности рассматривается история двух братьев-близнецов. Один из них (далее путешественник) отправляется в космический полёт, второй (далее домосед) — остаётся на Земле. Чаще всего «парадокс» формулируется следующим образом:

Формулировка I. С точки зрения домоседа часы движущегося путешественника имеют замедленный ход времени, поэтому при возвращении они должны отстать от часов домоседа. С другой стороны, относительно путешественника двигалась Земля, поэтому отстать должны часы домоседа. На самом деле братья равноправны, следовательно, после возвращения их часы должны показывать одно время.

Тем не менее, согласно СТО отставшими окажутся часы путешественника. В таком нарушении видимой симметричности братьев и усматривается противоречие.

Содержание

История

Эффект релятивистского замедления времени был сформулирован Альбертом Эйнштейном в его работе 1905 года в виде следующей теоремы:

Если в точке А находятся двое синхронно идущих часов и мы перемещаем одни из них по замкнутой кривой с постоянной скоростью до тех пор, пока они не вернутся в А (на что потребуется, скажем, t сек), то эти часы по прибытии в А будут отставать по сравнению с часами, остававшимися неподвижными… [1]

Классификация объяснений парадокса

Объяснить парадокс, подобный «парадоксу близнецов», можно при помощи двух подходов:

1) Выявить происхождение логической ошибки в рассуждениях, которые привели к противоречию; 2) Провести детальные вычисления величины эффекта замедления времени с позиции каждого из братьев.

Первый подход зависит от деталей формулировки парадокса. В разделах «Простейшие объяснения» и «Физическая причина парадокса» будут приведены различные версии «парадокса» и даны объяснения того, почему противоречия на самом деле не возникает.

В рамках второго подхода расчёты показаний часов каждого из братьев проводятся как с точки зрения домоседа (что обычно не представляет труда), так и с точки зрения путешественника. Так как последний менял свою систему отсчёта, возможны различные варианты учёта этого факта. Их условно можно разделить на две большие группы.

К первой группе относятся вычисления на основе специальной теории относительности в рамках инерциальных систем отсчёта. В этом случае этапы ускоренного движения считаются пренебрежимо малыми по сравнению с общим временем полёта. Иногда вводится третья инерциальная система отсчёта, движущаяся навстречу путешественнику, при помощи которой показания его часов «передаются» брату-домоседу. В разделе «Обмен сигналами» будет приведен простейший расчёт, основанный на эффекте Доплера.

Ко второй группе относятся вычисления, учитывающие детали ускоренного движения. В свою очередь, они делятся по признаку использования или неиспользования в них теории гравитации Эйнштейна (ОТО). Расчёты с использованием ОТО основаны на введении эффективного гравитационного поля, эквивалентного ускорению системы, и учёте изменения в нём темпа хода времени. Во втором способе неинерциальные системы отсчёта описываются в плоском пространстве-времени и понятие гравитационного поля не привлекается. Основные идеи этой группы расчётов будут представлены в разделе «Неинерциальные системы отсчёта».

Кинематические эффекты СТО

В основе СТО лежат преобразования Лоренца. Для понимания сути парадокса близнецов необходим аккуратный анализ основных кинематических эффектов, которые из них следуют. Рассмотрим две системы отсчёта и , пространственные оси которых параллельны друг другу. Пусть система движется относительно вдоль оси со скоростью , тогда:

где — координата и время события, измеренные в «неподвижной» системе отсчёта , а — координата и время того же события для наблюдателя, связанного с «движущейся» системой .

Замедление времени

Если часы неподвижны в системе , то для двух последовательных событий имеет место . Такие часы перемещаются относительно системы по закону , поэтому интервалы времени связаны следующим образом:

Важно понимать, что в этой формуле интервал времени измеряется одними движущимися часами . Он сравнивается с показаниями нескольких различных, синхронно идущих часов, расположенных в системе , мимо которых пролетают часы . В результате такого сравнения оказывается, что движущиеся часы идут медленнее неподвижных часов.

Важный аспект эффекта замедления времени связан с эквивалентностью инерциальных систем отсчёта (принцип относительности). Часы, неподвижные в системе : , движутся относительно синхронизированных часов в системе : . В результате, часы будут идти медленнее по сравнению с часами в системе :

Несмотря на совпадения обозначений в двух последних формулах, они не противоречат друг другу. Каждая из них описывает различные измерительные процедуры. В первом случае одни часы движутся мимо нескольких часов в , а во втором случае ситуация обратная, и одни часы движутся мимо нескольких часов в .

Относительность одновременности

Относительность одновременности событий является ключевым эффектом СТО, необходимым для понимания «парадокса близнецов». Рассмотрим несколько синхронизированных часов, расположенных вдоль оси в каждой из систем отсчёта. В преобразованиях Лоренца предполагается, что в момент времени начала систем отсчёта совпадают: . Ниже изображена такая синхронизация отсчёта времени (на «центральных» часах) с точки зрения системы отсчёта (левый рисунок) и с точки зрения наблюдателей в (правый рисунок):

Предположим, что рядом с каждыми часами в обеих системах отсчёта находятся наблюдатели. Положив в преобразованиях Лоренца , получаем . Это означает, что наблюдатели в системе , одновременно с совпадением времени на центральных часах, регистрируют различные показания на часах в системе . Для наблюдателей, расположенных справа от точки , с координатами 0″ border=»0″ />, в момент времени часы неподвижной системы отсчёта показывают «будущее» время: 0″ border=»0″ />. Наблюдатели , находящиеся слева от , наоборот, фиксируют «прошлое» время часов : . На рисунках выше положение стрелок символизирует подобную разницу показаний часов двух систем отсчёта.

Единое «настоящее», то есть часы, синхронно идущие в различных точках пространства, можно ввести только в рамках конкретной инерциальной системы отсчёта. Однако этого нельзя сделать одновременно для двух различных систем отсчёта.

Движущаяся относительно неподвижных наблюдателей система с их точки зрения содержит рассинхронизированные в направлении движения часы, своеобразное непрерывное объединение «прошлого», «настоящего» и «будущего».

Эффекты замедления времени и относительности одновременности тесно связаны друг с другом и одинаково необходимы для расчёта ситуации, описанной в «парадоксе» близнецов.

Простейшие объяснения

Благодаря своей продолжительной истории парадокс близнецов существует в разнообразных формулировках. Чаще всего тем или иным методом демонстрируется симметричность братьев, из которой должно было бы следовать противоречие с выводом СТО о том, что отстанут часы путешественника. Исходная версия парадокса (Формулировка I) не уточняет характера движения путешественника. Поэтому для неё справедливо следующее простое объяснение (на качественном уровне):

При этом, чем короче момент ускорения, тем оно больше, и как следствие больше разница в скорости часов на Земле и космического корабля, если он удалён от Земли в момент изменения скорости. Поэтому ускорением никогда нельзя пренебречь.

Конечно, сама по себе констатация несимметричности братьев не объясняет, почему замедлиться должны часы именно у путешественника, а не у домоседа. Кроме этого, часто возникает непонимание:

«Почему нарушение равноправия братьев в течение столь короткого времени (остановка путешественника) приводит к такому разительному нарушению симметрии?»

Чтобы глубже понять причины несимметричности и следствия, к которым они приводят, необходимо ещё раз выделить ключевые посылки, явно или неявно присутствующие в любой формулировке парадокса. Для этого будем считать, что вдоль траектории движения путешественника в «неподвижной» системе отсчёта, связанной с домоседом, расположены синхронно идущие (в этой системе) часы. Тогда возможна следующая цепочка рассуждений, как бы «доказывающих» противоречивость выводов СТО:

Итак, почему путешественник на самом деле будет наблюдать отставание своих часов от часов «неподвижной» системы, несмотря на то, что все такие часы с его точки зрения идут медленнее? Наиболее простым объяснением [28] в рамках СТО является то, что синхронизовать все часы в двух инерциальных системах отсчёта невозможно. Рассмотрим это объяснение подробнее.

Физическая причина парадокса

Во время полёта путешественник и домосед находятся в различных точках пространства и не могут сравнивать свои часы непосредственно. Поэтому, как и выше, будем считать, что вдоль траектории движения путешественника в «неподвижной» системе, связанной с домоседом, расставлены одинаковые, синхронно идущие часы, которые может наблюдать путешественник во время полёта. Благодаря процедуре синхронизации в «неподвижной» системе отсчёта введено единое время, определяющее в данный момент «настоящее» этой системы.

После старта путешественник «переходит» в инерциальную систему отсчёта , движущуюся относительно «неподвижной» со скоростью . Этот момент времени принимается братьями за начальный . Каждый из них будет наблюдать замедленный ход часов другого брата.

Однако, единое «настоящее» системы для путешественника перестаёт существовать. В системе отсчёта есть своё «настоящее» (множество синхронизированных часов). Для системы , чем дальше по ходу движения путешественника находятся части системы , тем в более отдалённом «будущем» (с точки зрения «настоящего» системы ) они находятся.

Непосредственно это будущее наблюдать путешественник не может. Это могли бы сделать другие наблюдатели системы , расположенные впереди по движению и имеющие синхронизированное с путешественником время.

Поэтому, хотя все часы в неподвижной системе отсчёта, мимо которых пролетает путешественник, идут с его точки зрения медленнее, из этого не следует, что они отстанут от его часов.

В момент времени , чем дальше впереди по курсу находятся «неподвижные» часы, тем больше их показания с точки зрения путешественника. Когда он достигает этих часов, они не успеют отстать настолько, чтобы скомпенсировать начальное расхождение времени.

Действительно, положим координату путешественника в преобразованиях Лоренца равной . Закон его движения относительно системы имеет вид . Время, прошедшее после начала полёта, по часам в системе меньше, чем в :

Другими словами, время на часах путешественника отстаёт от показаний часов системы . В то же время часы, мимо которых пролетает путешественник, неподвижны в : . Поэтому их темп хода для путешественника выглядит замедленным:

\Delta t.» border=»0″ />

несмотря на то, что все конкретные часы в системе идут медленнее с точки зрения наблюдателя в , разные часы вдоль его траектории будут показывать время, ушедшее вперед.

Разность темпа хода часов и — эффект относительный, тогда как значения текущих показаний и в одной пространственной точке — носят абсолютный характер. Наблюдатели, находящиеся в различных инерциальных системах отсчёта, но «в одной» пространственной точке, всегда могут сравнить текущие показания своих часов. Путешественник, пролетая мимо часов системы видит, что они ушли вперёд t'» border=»0″ />. Поэтому, если путешественник решит остановиться (быстро затормозив), ничего не изменится, и он попадёт в «будущее» системы . Естественно, после остановки темп хода его часов и часов в станет одинаковым. Однако, часы путешественника будут показывать меньшее время чем часы системы , находящиеся в точке остановки. В силу единого времени в системе часы путешественника отстанут от всех часов , в том числе и от часов его брата. После остановки путешественник может вернуться домой. В этом случае весь анализ повторяется. В результате, как в точке остановки и разворота, так и в исходной точке при возвращении путешественник оказывается моложе своего брата-домоседа.

Если же вместо остановки путешественника до его скорости ускорится домосед, то последний «попадёт» в «будущее» системы путешественника. В результате «домосед» окажется моложе «путешественника». Таким образом:

кто изменяет свою систему отсчёта, тот и оказывается моложе.

Обмен сигналами

Вычисление замедления времени с позиции каждого брата можно провести при помощи анализа обмена сигналами между ними. Хотя братья, находясь в различных точках пространства, не могут непосредственно сравнивать показания своих часов, они могут передавать сигналы «точного времени» при помощи световых импульсов или видеотрансляции изображения часов. Понятно, что при этом они наблюдают не «текущее» время на часах брата, а «прошлое», так как сигналу требуется время для распространения от источника к приёмнику.

При обмене сигналами необходимо учитывать эффект Доплера. Если источник удаляется от приёмника, то частота сигнала уменьшается, а когда он приближается — увеличивается:

где — собственная частота излучения, а — частота принимаемого наблюдателем сигнала. Эффект Доплера имеет классическую составляющую и составляющую релятивистскую, непосредственно связанную с замедлением времени. Скорость , входящая в соотношения изменения частоты, является относительной скоростью источника и приёмника.

Рассмотрим ситуацию, в которой братья передают друг другу каждую секунду (по своим часам) сигналы точного времени. Проведём сначала расчёт с позиции путешественника.

Расчёт путешественника

Время полёта по часам путешественника в одну сторону равно , и такое же в обратную. Количество принятых «земных секунд» в течение путешествия равно их частоте , умноженной на время. Поэтому при удалении от Земли путешественник получит существенно меньше «секунд»:

а при приближении, наоборот, больше:

t’_1.» border=»0″ />

Суммарное количество «секунд», полученных с Земли за время , больше, чем переданных на неё:

в точном соответствии с формулой замедления времени.

Расчёт домоседа

Несколько иная арифметика у домоседа. Пока его брат удаляется, он также регистрирует увеличенный период точного времени, передаваемый путешественником. Однако, в отличие от брата, домосед наблюдает такое замедление дольше. Время полёта на расстояние в одну сторону составляет по земным часам . Торможение и разворот путешественника домосед увидит спустя дополнительное время , требуемое свету для прохождения расстояния от точки разворота. Поэтому, только через время от начала путешествия домосед зарегистрирует ускоренную работу часов [rmr 4] приближающегося брата:

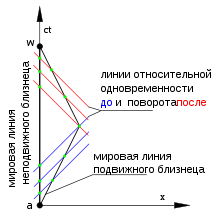
Время движения света от точки разворота выражается через время полёта к ней путешественника следующим образом (см. рисунок):

Поэтому количество «секунд», полученных от путешественника, до момента его разворота (по наблюдениям домоседа) равно:

Сигналы с повышенной частотой домосед принимает в течение времени (см. рисунок выше), и получает «секунд» путешественника:

Суммарное число полученных «секунд» за время равно:

Таким образом, соотношение для показания часов в момент встречи путешественника () и брата-домоседа () не зависит от того, с чьей точки зрения оно рассчитывается.

Геометрическая интерпретация

В пространстве Минковского мировая линия покоящегося (или двигающегося равномерно и прямолинейно) наблюдателя является отрезком прямой. Мировая линия путешественника, улетевшего с Земли и возвратившегося к ней, прямой не является (в простейшем случае мгновенного изменения скорости на противоположную в точке поворота она является ломаной, а при прохождении части пути с постоянным ускорением соответствующий участок линии будет дугой гиперболы). Так же как в обычной геометрии из всех линий, соединяющих две точки, самой короткой является прямая, так же и в пространстве Минковского из всех мировых линий, соединяющих две точки, самой длинной (а не самой короткой в силу псевдоевклидовости пространства-времени) является отрезок прямой.

Поскольку длина мировой линии наблюдателя, переместившегося в пространстве Минковского из точки a в точку w, с точностью до множителя c равна времени, которое было затрачено на это перемещение в его собственной системе отсчёта, мы имеем, что из всех наблюдателей, стартовавших в точке a и финишировавших в точке w, в системе отсчёта того наблюдателя, который покоился (или двигался равномерно и прямолинейно, если пространственные координаты точек a и w не совпадают), пройдёт наибольшее время.

Неинерциальные системы отсчёта

В произвольных системах отсчёта свойства пространства и времени определяются метрическим тензором , задающим интервал между двумя бесконечно близкими событиями:

где по повторяющимся индексам подразумевается суммирование (по греческим буквам от 0 до 3, а по латинским от 1 до 3), — временная координата, — пространственные. Собственное время часов вдоль их траектории определяется следующим образом:

Его величина является инвариантом, следовательно, вычисления проведенные в различных системах отсчёта, должны давать один и тот же результат.

Расчёт домоседа

Близнец, оставшийся на Земле, находится в инерциальной системе отсчёта, поэтому для него метрика может быть выбрана таким образом, что

В этом случае собственное время любых часов принимает простой вид:

где — скорость этих часов. Земные часы неподвижны (), и их собственное время равно координатному . Часы путешественника имеют переменную скорость . Так как корень под интегралом остаётся всё время меньше единицы, время этих часов, независимо от явного вида функции , всегда оказываются меньше . В результате .

Если разгон и торможение проходят релятивистски равноускоренно (с параметром собственного ускорения ) в течение , а равномерное движение — , то по часам корабля пройдёт время [29] :

, где — гиперболический арксинус

Рассмотрим гипотетический полёт к звёздной системе Альфа Центавра, удалённой от Земли на расстояние в 4,3 световых года. Если время измеряется в годах, а расстояния в световых годах, то скорость света равна единице, а единичное ускорение св.год/год² близко к ускорению свободного падения и примерно равно 9,5 м/c².

Пусть половину пути космический корабль двигается с единичным ускорением, а вторую половину — с таким же ускорением тормозит (). Затем корабль разворачивается и повторяет этапы разгона и торможения. В этой ситуации время полёта в земной системе отсчёта составит примерно 12 лет, тогда как по часам на корабле пройдёт 7,3 года. Максимальная скорость корабля достигнет 0,95 от скорости света.

За 64 года собственного времени космический корабль с единичным ускорением потенциально может совершить путешествие (вернувшись на Землю) к галактике Андромеды, удалённой на 2,5 млн св. лет. На Земле за время такого полёта пройдёт около 5 млн лет. Развивая вдвое большее ускорение (к которому тренированный человек вполне может привыкнуть при соблюдении ряда условий и использования ряда приспособлений, например, анабиоза), можно подумать даже об экспедиции к видимому краю Вселенной (около 14 млрд. св. лет), которая займёт у космонавтов порядка 50 лет; правда, возвратившись из такой экспедиции (через 28 млрд. лет по земным часам), её участники рискуют не застать в живых не то что Землю и Солнце, но даже нашу Галактику. Исходя из этих расчётов, разумный радиус доступности для межзвёздных экспедиций с возвратом не превышает нескольких десятков световых лет, если, конечно, не будут открыты какие-либо принципиально новые физические принципы перемещения в пространстве-времени. Впрочем, обнаружение многочисленных экзопланет даёт основания полагать, что планетные системы встречаются у достаточно большой доли звёзд, поэтому космонавтам будет что исследовать и в этом радиусе (например, планетные системы ε Эридана и Глизе 581).

Расчёт путешественника

Для проведения того же расчёта с позиции путешественника, необходимо задать метрический тензор, соответствующий его неинерциальной системе отсчёта. Относительно этой системы скорость путешественника нулевая, поэтому время на его часах равно

Заметим, что является координатным временем и в системе путешественника отличается от времени системы отсчёта домоседа.

Земные часы свободны, поэтому они движутся вдоль геодезической, определяемой уравнением [30] :

где — символы Кристоффеля, выражающиеся через метрический тензор . При заданном метрическом тензоре неинерциальной системы отсчёта эти уравнения позволяют найти траекторию часов домоседа в системе отсчёта путешественника. Её подстановка в формулу для собственного времени даёт интервал времени, прошедший по «неподвижным» часам:

где — координатная скорость земных часов.

Результат всех этих вычислений показывает, что и с точки зрения путешественника его часы отстанут от часов неподвижного наблюдателя. В итоге разница времени путешествия с обеих точек зрения будет одинаковая, и путешественник окажется моложе домоседа. Если длительность этапов ускоренного движения много меньше длительности равномерного полёта, то результат более общих вычислений совпадает с формулой, полученной в рамках инерциальных систем отсчёта.

Выводы

Рассуждения, проводимые в истории с близнецами, приводят только к кажущемуся логическому противоречию. При любой формулировке «парадокса» полной симметричности между братьями нет. Кроме этого, важную роль для понимания того, почему время замедляется именно у путешественника, менявшего свою систему отсчёта, играет относительность одновременности событий.

Расчёт величины замедления времени с позиции каждого брата может быть выполнен как в рамках элементарных вычислений в СТО, так и при помощи анализа неинерциальных систем отсчёта. Все эти вычисления согласуются друг с другом и показывают, что путешественник окажется моложе своего брата-домоседа.

Парадоксом близнецов часто также называют сам вывод теории относительности о том, что один из близнецов состарится сильнее другого. Хотя такая ситуация и необычна, в ней нет внутреннего противоречия. Многочисленные эксперименты по удлинению времени жизни элементарных частиц и замедлению хода макроскопических часов при их движении подтверждают теорию относительности. Это даёт основание утверждать, что замедление времени, описанное в истории с близнецами, произойдёт и при реальном осуществлении этого мысленного эксперимента.

Источник