как узнать какой шифр используется
Шифр Виженера
Калькулятор шифрует входной текст на русском языке шифром Виженера. Неалфавитные символы (пробелы, знаки препинания, цифры) — не преобразуются.
Так как Шифр Цезаря у нас уже есть, было бы логично дополнить его калькулятором, который шифрует/расшифровывает текст используя шифр Виженера.
Суть алгоритма шифрования проста. Шифр Виженера — это последовательность шифров Цезаря с различными значениями сдвига (ROTX — см. Шифр Цезаря). То есть к первой букве текста применяется преобразование, например, ROT5, ко второй, например, ROT17, и так далее. Последовательность применяемых преобразований определяется ключевой фразой, в которой каждая буква слова обозначает требуемый сдвиг, например, фраза ГДЕ ОН задает такую последовательность шифров Цезаря: ROT3-ROT4-ROT5-ROT15-ROT14, которая повторяется, пока не будет зашифрован весь текст сообщения.
Как повествует Википедия, шифр Виженера является шифром подстановки, то есть шифром, в котором каждая буква исходного текста заменяется буквой шифр-текста. Для вскрытия подобных шифров используется частотный криптоанализ.
Еще там можно прочитать про вариант шифра с бегущим ключом (running key), который был когда-то был невзламываемым. Этот вариант заключается в использовании в качестве ключа блока текста, равного по длине исходному тексту. Впрочем, и этот вариант, как оказалось, успешно поддается взлому. Проблема с бегущим ключом шифра Виженера состоит в том, что криптоаналитик имеет статистическую информацию о ключе (учитывая, что блок текста написан на известном языке) и эта информация будет отражаться в шифрованном тексте. Если ключ действительно случайный, его длина равна длине сообщения и он использовался единожды, то шифр Виженера теоретически будет невзламываемым, но такие системы уже относятся к классу систем одноразового кода, или одноразового шифр-блокнота (one-time pad). Они действительно не поддаются взлому, однако их практическое применение довольно затруднительно.
10 популярных кодов и шифров
Авторизуйтесь
10 популярных кодов и шифров
Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.
В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.
Стандартные шифры
Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».
Попробуйте расшифровать сообщение:
Сумели? Напишите в комментариях, что у вас получилось.
Шифр транспонирования
В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.
Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:
Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:
Азбука Морзе
В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов: 
Сможете расшифровать сообщение, используя картинку?
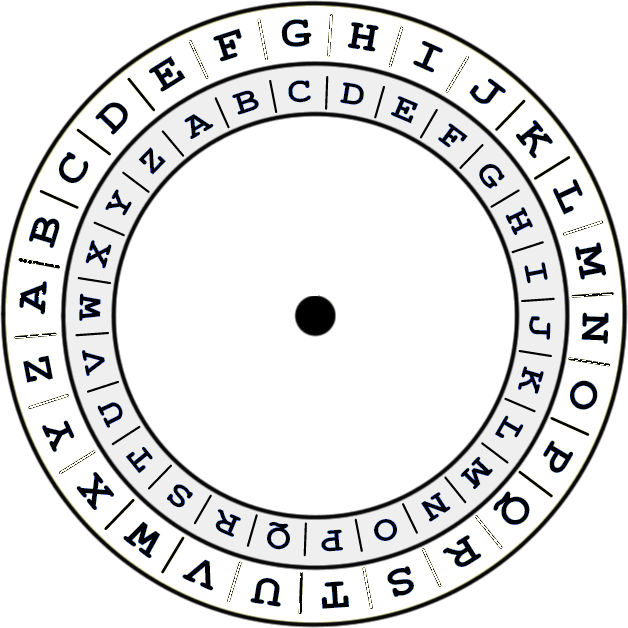
Шифр Цезаря
Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.
А здесь использован шифр Цезаря с шагом 5:
Моноалфавитная замена
Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.
Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».
Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.
Шифр Виженера
Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.
В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для (k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.
Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.
Попробуйте расшифровать эту фразу самостоятельно:
Подсказка длина кодового слова — 4.
Шифр Энигмы
Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.
Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.
Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.
Цифровые шифры
В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.
Двоичный код
Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.
Расшифруйте следующее сообщение, в котором использована кириллица:
Шифр A1Z26
Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите. Только нижний регистр.
Попробуйте определить, что здесь написано:
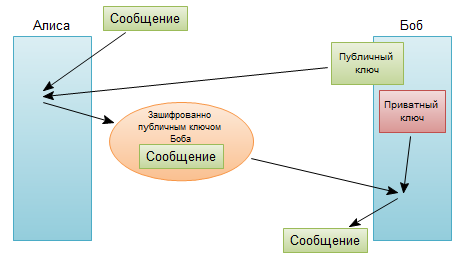
Шифрование публичным ключом
Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.
Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.
Как расшифровать код или шифр?
Для этого применяются специальные сервисы. Выбор такого инструмента зависит от того, что за код предстоит расшифровать. Примеры шифраторов и дешифраторов:
Популярные коды и шифры.
В рубрике “Информационная безопасность” мы разбирали общие вопросы о криптографии и методах шифрования. В этой статье мы рассмотрим самые популярные коды и шифры.
В мире существует множество шифров и кодов для засекречивания различных посланий. Вопреки распространенному мнению, код и шифр — это не одно и то же. В коде каждое слово заменяется на какое-то иное кодовое слово, в то время как в шифре заменяются сами символы сообщения.
1. Шифр Цезаря
Шифр Цезаря так называется, потому что его использовал сам Юлий Цезарь. Шифр Цезаря — это не один шифр, а целых двадцать шесть, использующих один и тот же принцип. Например, шифр ROT1 относится к шифру Цезаря.
Получателю нужно сказать, какой из шифров используется. Если используется шифр «G», тогда А заменяется на G, B на H, C на I и т.д. Если используется шифр «Y», тогда А заменяется на Y, B на Z, C на A и т.д. На шифре Цезаря базируется огромное число других, более сложных шифров.
Шифр Цезаря очень простой и быстрый, но он является шифром простой одинарной перестановки и поэтому легко взламывается.
2. Азбука Морзе
Азбука является средством обмена информации и ее основная задача – сделать сообщения более простыми и понятными для передачи. В системе Морзе каждая буква, цифра и знак препинания имеют свой код, составленный из группы тире и точек. При передаче сообщения с помощью телеграфа тире и точки означают длинные и короткие сигналы. Пример:
3. Стеганография
Стеганография старше кодирования и шифрования. Это искусство появилось очень давно. Оно буквально означает «скрытое письмо» или «тайнопись». Хоть стеганография не совсем соответствует определениям кода или шифра, но она предназначена для сокрытия информации от чужих глаз. Про стеганографию можно почитать в нашей отдельной статье.
4. ROT1
Данный шифр известен всем с детства. Каждая буква шифра заменяется на следующую за ней в алфавите. Так, A заменяется на B, B на C, и т.д.
«ROT1» значит «ROTate 1 letter forward through the alphabet» («сдвиньте алфавит на одну букву вперед»).
5. Моноалфавитная замена
Описанные выше ROT1 и азбука Морзе являются представителями шрифтов моноалфавитной замены. Приставка «моно» означает, что при шифровании каждая буква изначального сообщения заменяется другой буквой или кодом из единственного алфавита шифрования.
Дешифрование шифров простой замены не составляет труда, и в этом их главный недостаток. Разгадываются они простым перебором или частотным анализом.
6. Транспозиция
В транспозирующих шифрах буквы переставляются по заранее определенному правилу. Например, если каждое слово пишется задом наперед, то из «all the better to see you with» получается «lla eht retteb ot ees joy htiw».
В Гражданскую войну в США и в Первую мировую его использовали для передачи сообщений.
7. Шифр Виженера
Шифр Виженера использует тот же принцип, что и шифр Цезаря, за тем исключением, что каждая буква меняется в соответствии с кодовым словом.
Данный шифр на порядок более устойчив к взлому, чем моноалфавитные, хотя представляет собой шифр простой замены текста. Пример:
Давайте зашифруем слово “Пароль” с помощью данного шифра. Ключевое слово будем использовать “Код”. Нарисуем таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Фраза: | п | а | р | о | л | ь |
| Ключ | к | о | д | к | о | д |
Берем первые буквы ключа и нашего слова и скрещиваем между собой с помощью таблицы Виженера и получается буква “ъ” и идем далее. Остальное попробуйте самостоятельно и напишите ответ в комментариях
8. Настоящие коды
В настоящих кодах каждое слово заменяется на другое. Расшифровывается такое послание с помощью кодовой книги, где записано соответствие всех настоящих слов кодовым, прямо как в словаре.
Многие страны использовали коды, периодически их меняя, чтобы защититься от частотного анализа. Но есть минус: если кодовая книга будет украдена, то с ее помощью больше будет невозможно что-либо зашифровать, и придется придумывать новый код, что требует огромных усилий и затрат времени.
9. Шифр Энигмы
Энигма — это шифровальная машина, использовавшаяся нацистами во времена Второй Мировой. Принцип ее работы таков: есть несколько колес и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.
Существовало более ста триллионов возможных комбинаций колес, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.
10. Шифр Гронсфельда
Шифр Гронсфельда — это модификация шифра Цезаря. Данный способ является значительно более стойким к взлому и заключается в том, что каждый символ кодируемой информации шифруется при помощи одного из разных алфавитов, которые циклически повторяются. Можно сказать, что это многомерное применение простейшего шифра замены.
11. Шифрование методом публичного ключа
Суть данного шифра заключается, как правило, в наличии двух ключей, один из которых передается публично, а второй является секретным (приватным). Открытый ключ используется для шифровки сообщения, а секретный — для дешифровки.
В роли открытого ключа чаще всего выступает очень большое число, у которого существует только два делителя, не считая единицы и самого числа. Вместе эти два делителя образуют секретный ключ.
10 популярных кодов и шифров
Необходимость засекречивать важные послания возникла еще в древности. Со временем люди находили новые, все более сложные способы делать послания недоступными чужим глазам. Вопреки распространенному мнению, код и шифр — это не одно и то же. В коде каждое слово заменяется на какое-то иное кодовое слово, в то время как в шифре заменяются сами символы сообщения. Когда люди говорят «код», они, как правило, имеют в виду «шифр». Древние рукописи и языки были поняты с помощью техник декодирования и дешифрования. Самый известный пример — Розеттский камень Древнего Египта. Фактически коды и шифры определяли исход многих войн и политических интриг на протяжении всей истории человечества. Существуют тысячи типов шифрования сообщений, но в этой статье мы рассмотрим лишь 10 самых известных и значимых из них.
10. Стеганография
Стеганография — это искусство скрытого письма. Этой технике даже больше лет, чем кодам и шифрованию. Например, сообщение может быть написано на бумаге, покрыто ваксой и проглочено с той целью, чтобы незаметно доставить его получателю. Другой способ — нанести сообщение на бритую голову курьера, подождать, пока волосы вырастут заново и скроют послание. Лучше всего для стенографии использовать повседневные объекты.
9. ROT1
Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, A заменяется на B, B на C, и т.д. «ROT1» значит «ROTate 1 letter forward through the alphabet» (англ. «сдвиньте алфавит на одну букву вперед»). Сообщение «I know what you did last summer» станет «J lopx xibu zpv eje mbtu tvnnfs». Этот шифр весело использовать, потому что его легко понять и применять, но его так же легко и расшифровать. Из-за этого его нельзя использовать для серьезных нужд, но дети с радостью «играют» с его помощью. Попробуйте расшифровать сообщение «XBT JU B DBU J TBX?».
8. Транспозиция
В транспозирующих шифрах буквы переставляются по заранее определенному правилу. Например, если каждое слово пишется задом наперед, то из «all the better to see you with» получается «lla eht retteb to ees joy htiw». Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет «la tl eh eb tt re to es ye uo iw ht». Подобные шифры использовались в Первую Мировую и Американскую Гражданскую Войну, чтобы посылать важные сообщения. Сложные ключи могут сделать такой шифр довольно сложным на первый взгляд, но многие сообщения, закодированные подобным образом, могут быть расшифрованы простым перебором ключей на компьютере. Попробуйте расшировать «THGINYMROTSDNAKRADASAWTI».
7. Азбука Морзе
В азбуке Морзе каждая буква алфавита, все цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов, часто называемых «точками и тире». Так, A — это «•—», B — «—•••», и т.д. В отличие от большинства шифров, азбука Морзе используется не для затруднения чтения сообщений, а наоборот, для облегчения их передачи (с помощью телеграфа). Длинные и короткие сигналы посылаются с помощью включения и выключения электрического тока. Телеграф и азбука Морзе навсегда изменили мир, сделав возможной молниеносную передачу информации между разными странами, а также сильно повлияли на стратегию ведения войны, ведь теперь можно было можно осуществлять почти мгновенную коммуникацию между войсками.
6. Шифр Цезаря
Шифр Цезаря называется так, как ни странно, потому что его использовал сам Юлий Цезарь. На самом деле шифр Цезаря — это не один шифр, а целых двадцать шесть, использующих один и тот же принцип! Так, ROT1 — всего один из них. Получателю нужно сказать, какой из шифров используется. Если используется шифр «G», тогда А заменяется на G, B на H, C на I и т.д. Если используется шифр «Y», тогда А заменяется на Y, B на Z, C на A и т.д. На шифре Цезаря базируется огромное число других, более сложных шифров, но сам по себе он не представляет из себя интереса из-за легкости дешифровки. Перебор 26 возможных ключей не займет много времени. Li bra ghflskhu wklv dqg bra nqrz lw, fods brxu kdqgv.
5. Моноалфавитная замена
ROT1, азбука Морзе, шифр(ы) Цезаря относятся к одному и тому же типу шифров — моноалфавитной замене. Это значит, что каждая буква заменяется на одну и только одну другую букву или символ. Такие шифры очень легко расшифровать даже без знания ключа. Делается это при помощи частотного анализа. Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А». Человек, расшифровывающий моноалфавитный шифр, может смотреть на частоту встречающихся букв и почти законченные слова. Так, «T_E» с большой долей вероятности окажется «ТНЕ». К сожалению, этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов, чтобы с достаточной достоверностью выявить соответствие наиболее часто встречающихся символов буквам из обычного алфавита. Мария Стюарт использовала невероятно сложный моноалфавитный шифр с несколькими вариациями, но когда его наконец-то взломали, прочитанные сообщения дали ее врагам достаточно поводов, чтобы приговорить ее к смерти. Ptbndcb ymdptmq bnw yew, bnwzw raw rkbcriie wrze bd owktxnwa.
4. Шифр Виженера
Этот шифр сложнее, чем моноалфавитные. Представим, что у нас есть таблица, построенная по тому же принципу, что и приведенная выше, и ключевое слово, допустим, «CHAIR». Шифр Виженера использует тот же принцип, что и шифр Цезаря, за тем исключением, что каждая буква меняется в соответствии с кодовым словом. В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова (в нашем случае «С»), вторая буква — согласно алфавиту для второй буквы кодового слова («H»), и так далее. В случае, если послание длиннее кодового слова, то для (k*n+1)-ой буквы (где n — это длина кодового слова) вновь будет использован алфавит для первой буквы кодового слова, и так далее. Очень долгое время шифр Виженера считался невзламываемым. Чтобы его расшифровать, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания, где n — предполагаемая длина кодового слова. Если длина была угадана верно, то и сам шифр вскроется с большей или меньшей долей вероятности. Если предполагаемая длина не дает верных результатов, то пробуют другую длину кодового слова, и так далее до победного конца. Eoaqiu hs net hs byg lym tcu smv dot vfv h petrel tw jka.
3. Настоящие коды
В настоящих кодах каждое слово заменяется на другое. Расшифровывается такое послание с помощью кодовой книги, где записано соответствие всех настоящих слов кодовым, прямо как в словаре. Преимущества такого способа в том, что сообщению необходимо быть ЧРЕЗВЫЧАЙНО длинным, чтобы можно было его взломать с помощью частотного анализа, так что коды полезнее некоторых шифров. Многие страны использовали коды, периодически их меняя, чтобы защититься от частотного анализа. Тем не менее, есть и минус: кодовая книга становится критическим предметом, и в случае, если она будет украдена, то с ее помощью больше будет невозможно что-либо зашифровать, и придется придумывать новый код, что требует огромных усилий и затрат времени. Обычно коды используют только богатые и влиятельные люди, которые могут поручить работу по их составлению другим.
2. Шифр Энигмы
Энигма — это шифровальная машина, использовавшаяся нацистами во времена Второй Мировой. Принцип ее работы таков: есть несколько колес и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес. Соль в том, что существовало более ста триллионов возможных комбинаций колес, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения. Все Энигмы были идентичными, так что при одинаковом начальном положении колес на двух разных машинах и текст выходил одинаковый. У немецкого командования были Энигмы и список положений колес на каждый день, так что они могли с легкостью расшифровывать сообщения друг друга, но враги без знания положений послания прочесть не могли. Когда Энигма попала в руки к союзникам, они все равно сперва не могли ничего с ней сделать, потому что не знали положений-ключей. Дело по взлому шифра Энигмы было начато в польской разведке и доведено до конца в британской с помощью ученых и специальных машин (например, Turing Bombe, чья работа заключалась в том, чтобы моделировать одновременно работу сразу нескольких десятков Энигм). Отслеживание коммуникаций нацистов дало армии союзников важное преимущество в войне, а машины, использовавшиеся для его взлома, стали прообразом современных компьютеров.
1. Шифрование публичным ключом
Алгоритм шифрования, применяющийся сегодня в различных модификациях буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это некое очень большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53. Открытый ключ используется для того, чтобы зашифровать сообщение, а секретный — чтобы расшифровать. Без секретного ключа расшифровать сообщение невозможно. Когда вы отправляете свои личные данные, допустим, банку, или ваша банковская карточка считывается банкоматом, то все данные шифруются открытым ключом, а расшифровать их может только банк с соотвествующим секретным ключом. Суть в том, что математически очень трудно найти делители очень большого числа. Вот относительно простой пример. Недавно RSA выделила 1000 долларов США в качестве приза тому, кто найдет два пятидесятизначных делителя числа 1522605027922533360535618378132637429718068114961
380688657908494580122963258952897654000350692006139.
Понравилась статья? Подпишитесь на канал, чтобы быть в курсе самых интересных материалов
Шифры замены и табличного гаммирования
В данной работе рассматриваются шифры замены и табличного гаммирования. Читателю предлагается поучаствовать в процессе решения несколько задач из области защиты информации.
Допустим, что устройства читателя подвергаются атаке со стороны неизвестного хакера.
Нарушитель, хакер, злоумышленник не ограничивается выводом из строя устройств. Он их перепрограммирует с целью принудить владельца выполнять какие-то требования либо банального вымогательства у владельца устройств некоторой денежной суммы. Объявляет о требованиях, например, звонком по сотовому телефону и диктует условия (цену) за восстановление работоспособного состояния устройства. Информационная подсистема приборов защищена шифрами разной сложности. Нарушитель использует свои параметры этих разных шифров для затруднения владельцу самостоятельно восстановить работоспособность устройств.
Некоторые положения теории криптологии
Математическая модель произвольного шифра замены SА = (Х, К, Y, E, D), где
X – символ (фрагмент) открытого текста в алфавите А, |A| = n;
Y– символ шифртекста в алфавите В, |B| = m;
K – ключ шифра k =1(1)K; Ek – преобразование зашифрования с ключом kз;
Dk – преобразование расшифрования с ключом kp.
Требования к криптографической системе (КГС)
реализуемость и неизменность шифралгоритма программная и аппаратная;
преобразования, используемые в шифралгоритме должны быть обратимыми;
владение шифралгоритмом не должно способствовать вскрытию ключ;
совпадение объемов (длина шифрованного равна длине исходного) текстов;
любой возможный ключ должен обеспечивать равновероятную защиту;
отсутствие просто устанавливаемых зависимостей между ключами в сеансах связи;
прочтение шифртекста только с соответствующим ключом;
малые изменения ключа должны существенно менять шифртекст прежнего исходного;
малые изменения исходного текста при одном ключе существенно меняют шифртекст;
дополнительные символы к исходному тексту надежно скрываются в шифтексте;
число операций в атаке перебором ключей ограничивается возможностями компьютера;
число операций при атаке на ключ должно быть не меньше числа возможных ключей.
Требования к криптографическим примитивам [8]
биективность (при n=m), регулярность или (n,m,k)-эластичность векторного отображения;
высокая степень корреляционной иммунности;
большая алгебраическая степень и высокая нелинейность;
низкие автокорреляционные показатели, обеспечение строгого лавинного критерия.
Открытый текст прочитывается в первой строке, затем последний символ второй строки и далее справа налево, не прерываясь, в третьей и четвертой строках. Слова в клетки вписаны без пробелов
Для защиты информационной подсистемы «умного» устройства используется простая криптографической система, использующая алфавит естественного языка (русского). В сценарии участвуют два субъекта: владелец устройства и хакер. Владелец знает, что алфавит естественного языка (ЕЯ) предварительно подвергается преобразованию путем умножения на известную ему перестановку 32 степени. Буквы е и ё считаются одной буквой поэтому размерность алфавита не 33, а 32 буквы. Тексты пишутся без пробелов.
Задача читателя, который получил доступ к смешанному алфавиту, состоит в полном восстановлении работоспособности умного устройством (текстов команд), получении возможности замены смешанного алфавита другим (собственным) и зашифровании на его основе текстов (команд управления), которые появляются на экране устройства.
Отметим, что при работе с шифрами учитываются законы естественных языков (ЕЯ):
закон избыточности текстов,
закон частоты встречаемости элементов (букв, слов, n-грамм ) текста,
Простая одноалфавитная замена (без ключа)
Задача №1
Устройство перестало подчиняться командам (отказало), подверглось атаке нарушителя. После простейших проверок наличия внешних дефектов, энергоинтерфейсов, запаха горелой проводки изоляции не чувствуется, а на экранчике дисплея появилось (см. ниже
Зашифрованное сообщение №1
ъ ы п т к ю з г ю я ъ ы п ч к с ы э
Это набор из 18 символов <ъыпткюзгюяъыпчксыэ>, кажущийся бессмысленным. Но на самом деле нарушитель что-то сообщает владельцу на экране и исключает возможность использования устройства по назначению. Попробуем расшифровать оставленное злоумышленником сообщение. Для этого сформируем в таблице 1 перестановку, т.е. последовательность символов (букв) смешанного алфавита (четвертая строка).
Вторая строка частота встречаемости букв (в тысячных долях) естественного алфавита (третья строка), последняя (четвертая строка) содержит переставленные перестановкой Р 32 степени буквы ЕЯ
Шифрование текста нарушителем. В регистр загружается открытый текст и заменяем каждую его букву символом из 4-й строки (табл. 1), этот символ появляется на экране устройства (вторая строка таблицы 2)
При расшифровании символы верхней строки вписываются по мере их раскрытия, а вторая строка заполняется, считывается с экрана, взломанного устройства
Расшифрование текста с экрана. С каждым символом хакерского шифртекста экрана последовательно входим в таблицу 1 (нижняя строка) и в третьей ее строке находим соответствующий символ исходного (не шифрованного, открытого) текста хакера. Пройдя все 18 символов удается восстановить текст от хакера, его пожелание владельцу устройства «прочитайте про шифры».
Одноалфавитная замена с ключом
Задача №2
Для увеличения стойкости шифра к атакам, использующим частотный закон ЕЯ, в этом шифре используется не только смешанный алфавит, но вводится новый элемент в алгоритм шифрования, называемый ключом.
Определение. Ключом называется секретная последовательность символов алфавита (слово) фиксированной длины, возможно осмысленная, что совсем не обязательно, используемая при преобразовании открытого текста в шифрованный и обратно.
Таким образом, к характеристикам ключа относятся:
доступность – закрытый, открытый (в двухключевых шифрах),
алфавит – языка страны,
длина – число букв (символов),
состав – названия всех букв ключа,
порядок – следование букв состава ключа (осмысленный или нет),
срок – длительность использования.
Введение в алгоритм шифрования нового элемента «ключа» способствует при замене символа «х» открытого текста символом «у» шифрованного текста при очередном повторном появлении символа «х» заменить его не символом «у», как первый раз, а каким-то другим, на который укажет символ ключа. Подсчет нарушителем встречаемости символов открытого и шифрованного текста, не позволяет ему правильно сопоставлять пары таких символов, так как частота символов шифртекста стала отличной от прежней. Действительно, одному символу открытого текста стали соответствовать несколько разных символов шифртекста. Наглядно это увидим на конкретном примере.
Пусть, как и раньше, на экране устройства хакер написал свой текст (он изменился):
Зашифрованное сообщение №2
ю я и ю ю я и ю ю я и ю ю я и ю ю я
Этот текст возник иначе, чем в задаче 1, т.е. другим путем (с использованием ключа) отличным от способа шифрования в задаче 1. В качестве ключа используется короткое 4-х буквенное слово «ТЕСТ».
Шифрование. В таблице 3 верхняя строка заполнена открытым текстом хакера, а под ней выписан многократно без пробелов ключ ТЕСТ. В третью строку вписываются символы шифрованного текста, взятые из последней строки таблицы 1
Заливкой выделены повторяющиеся группы из 4-х символов, что может указывать на длину ключа
Задача №3
Шифрование. Для увеличения стойкости шифра к атакам, использующим частотный закон ЕЯ, в этом шифре используется не только смешанный алфавит, но вводится новый элемент в алгоритм шифрования, называемый ключом. Как влияет длина ключа на шифртекст? Изменим (увеличим на 1 символ) длину ключа. В таблице 4 верхняя строка заполнена открытым текстом хакера, а под ней выписан многократно без пробелов ключ ТЕКСТ. В третью строку вписываются символы смешанного алфавита, взятые из последней строки таблицы 1
Пусть, как и раньше, на экране устройства хакер (нарушитель) написал свой текст:
Зашифрованное сообщение №3 (текст опять изменился)
ю я л и ю ю я л и и ю ю я л и ю ю я л
Получилась очень похожая на предыдущую картинка, просто повторов стало меньше, а длина ключа возросла на 1 символ.
Многоалфавитная замена с ключом, гаммирование
Рассмотрение проблемы с атакой на шифры, которая использует частотные зависимости ЕЯ, привело к мысли использовать в алгоритме шифрования не только ключ, что как мы видели в задачах 2,3 оказалось не очень удачным решением (легко определяется длина ключа, повторяющиеся символы), но и более чем один (множество) смешанных алфавитов.
Ниже мы подробно рассмотрим схему шифрования с этими нововведениями и некоторые факторы, влияющие на стойкость шифра к атакам
Задача №4
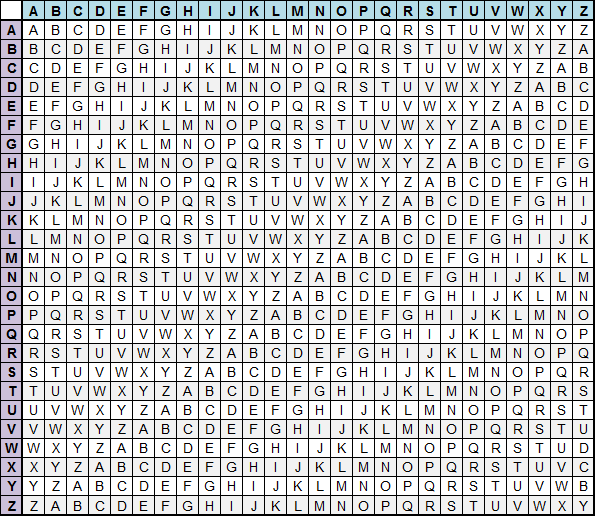
В этой задаче используется множество смешанных алфавитов, организованных в квадрат Виженера, а ключи используются прежние.
Для увеличения стойкости шифра к атакам, использующим частотный закон ЕЯ, в этом шифре используется не единственный смешанный алфавит, а их множество с применением циклического сдвига каждого последующего на один символ относительно предыдущего. Вытолкнутый циклическим сдвигом символ из начала алфавита помещается в конец списка букв алфавита так, что полная длина алфавите не меняется.
При одноалфавитной замене без ключа всегда символ «х» (буква) исходного (открытого) текста заменялась одной и той же буквой «у» смешанного алфавита, и частота использования х и у была одинаковой, совпадающей с частотой встречаемости символа «х» в ЕЯ. При многоалфавитной замене нарушитель понимает, что символ «х» при каждом очередном появлении в открытом тексте заменяется разными буквами из разных смешанных алфавитов. Этот факт не дает возможности нарушителю напрямую воспользоваться частотным законом ЕЯ, так как частота встречаемости символов открытого текста осталась прежней, но частота встречаемости символов шифрованного текста стала совершенно другой.
Зашифрованное сообщение №4 (текст опять изменился)
у и р г а т н э ь л з ш з ц ч ж ш з
Что же такое нарушитель желает сообщить владельцу «умного» устройства? Стремление разобраться в шифрованном сообщении приводит к необходимости детального анализа ситуации с шифрами и текстами открытыми и шифрованными. Прежде всего, необходимо уяснить как будет использоваться множество смешанных алфавитов, какое их количество задействуется в алгоритме и как эти алфавиты соотносятся друг с другом. Ответ на эти вопросы помогает найти новая таблица 5, названная квадратом 32×32 (таблицей) Виженера. Сколько смешанных алфавитов следует привлекать в алгоритме шифра? Как выбрать ключ шифра?
Строкам таблицы Виженера соответствуют символы (буквы) ключа. Из этого следует, что при шифровании используются столько строк квадрата Виженера, сколько букв содержит ключ шифра (при условии отсутствия повторов). Так как ключом может быть произвольная последовательность букв, то строкам квадрата соответствует полный алфавит. Колонкам квадрата соответствуют символы исходного текста – также полный алфавит.
Таким образом, в этом квадрате размещаются 32 смешанных алфавита (см таблица 1) по горизонтали и по вертикали. Каждый алфавит в этих линиях сдвигается (изменяется) на один символ относительно предыдущей линии, и этот символ вписывается после последнего символа в конце списка. Верхняя строка и вторая колонка – это алфавит ЕЯ с исходным упорядочением букв, т.е. каждая строка и столбец помечены буквой стандартного алфавита.
Из множества возможных перемешиваний алфавита Б. Виженер предложил использовать только n = 32. Способ их получения из первого путем циклического сдвига на каждом шаге на одну позицию.
Процесс шифрования. Исходный текст без пробелов вписывается в линейный регистр. Каждой букве отводится своя ячейка регистра. Ниже этого регистра помещается другой регистр, в который вписывается ключ ТЕСТ шифра. Если ключ шифра короче текста, то ключ вписывается многократно один за другим без пробелов. Таким образом, каждая буква исходного текста соответствует некоторой букве ключа. Это можно отобразить так «хи» → «хk».
Первой букве открытого (столбец) текста соответствует первая буква ключа (строка)
«хи =П»→«хk=т». Переходим в квадрат Виженера. Строка квадрата обозначена буквой «т» ключа, а столбец квадрата определяется буквой открытого текста «П». В клетке пересечения выбранных линий (строки, столбца) находится буква шифртекста «уш = у». Формально эти действия описываются цепочкой «хk = т» → «хи = П» → «уш = у» из трех символов: тПу.
Дальше все повторяется до исчерпания открытого текста. Результатом такого шифрования является третья строчка таблицы 6. Именно она появляется на экране дисплея умного устройства.
Анализ текста с экрана. Из примера для ключа «ТЕСТ» видим, что первая буква ИТ П заменяется на У, которая взята в строке квадрата, помеченной буквой Т ключа, и в колонке квадрата, соответствующей (помеченной) букве П.
Второй раз, когда буква П встречается в ИТ замена (буква 3) для нее берется в строке, ключа, помеченной буквой С (не как раньше буквой т), и в той же самой колонке для буквы П. Уже отсюда видим, что подсчет частот встречаемости буквы П в исходном тексте и символов замены для этой буквы в шифрованном тексте не совпадают, что не позволяет напрямую воспользоваться законом частоты повторяемости букв при вскрытии шифртекста.
Во-первых, в ключе могут быть повторяющиеся буквы и для них используется одна и та же строка квадрата Виженера:
Во-вторых, не исключается возможность совпадений (наложений) одинаковых непрерывных участков ИТ на одинаковые непрерывные участки ключа.
К чему это может привести будет рассмотрено на примере оцифровки для второго более длинного ключа «ТЕКСТ».
Анализ исходного текста и шифртекста с ключом ТЕСТ показывает следующее: в ИТ имеются две повторяющиеся триграммы «ПРО», в скобках за буквами пишем какими буквами они заменились в шифртексте: Р(И, Ш, Ш) встречается три раза; буквы П (У, З), О(Р З), Т(Т, Ь), И(А, Б) – по два раза; Ч(Г), А(Н),Й(Э),Е(Л),Ш(Ц),Ф(Ж),Ы(З).
Наш ограниченного объема пример позволил продемонстрировать все возможности замен. Хотя ключ ТЕСТ содержит четыре буквы, но различных среди них только три. Следовательно, при шифровании будут использованы только три различных смешанных алфавита.
Задача №5
Процесс шифрования. В этой задаче также используется множество смешанных алфавитов, организованных в квадрат Виженера. Используется более длинный ключ ТЕКСТ.
Первой букве открытого текста соответствует первая буква ключа «хи =П»→«хk=т».
Переходим в квадрат Виженера. Строка квадрата обозначена буквой «т» ключа, а столбец квадрата определяется буквой открытого текста «П». В клетке пересечения выбранных строки и столбца находится буква шифртекста «уш = у». Формально эти действия описываются цепочкой «хk = т» → «хи = П» → «ущ = у» из трех символов: тПу.
Дальше все повторяется до исчерпания открытого текста. Результатом такого шифрования является третья строчка таблицы 7. Именно она появляется на экране дисплея умного устройства.
Зашифрованное сообщение №5
у и ч к а ь я о в т у и ч г а ж и я
Будем пытаться прочесть это сообщение в ходе анализа шифртекста.
Анализ и дешифрование текста с экрана. Ключ ТЕКСТ содержит пять букв, из них различных только четыре, и с этим ключом будут использованы четыре различных смешанных алфавита. Какой же из ключей обеспечивает большую устойчивость к взлому (расшифрованию)?
Казалось-бы, тот шифр, который использует большее число различных алфавитов, что приводит к замене одной и той же буквы ИТ большим числом других букв, и лучше ее маскирует. Но, увы, это не общее правило. Наш пример призван это подтвердить.
Все ситуации замены при шифровании могут быть описаны следующим перечнем:
одинаковые буквы ИТ (П(УУ), Р(ИИИ), О(ЧЧ), И(АА),) заменяются одинаковыми в ШТ (У, И, Ч, А);
одинаковые буквы ИТ (Т) заменяются разными в ШТ (Ь, В);
разные буквы ИТ(Ч, А, Й, Е, Ш, Ф, Ы) заменяются разными в ШТ(К, Я, О, Т, Г, Ж, Я);
разные буквы ИТ (А, Ы) заменяются одинаковыми в ШТ (Я).
Определение длины ключа. Причиной появления одной и той же буквы Y в ШТ может быть либо совпадение буквы X в ИТ и буквы ключа под ней; либо на Y была заменена другая буква из ИТ при использовании сдвинутого смешанного алфавита.
Действительно, в исходном тексте буква Р попадает трижды на букву Е ключа ТЕКСТ во 2-й, 12-й и 17-й позициях и заменяется буквой И из одного и того же смешанного циклически сдвинутого алфавита. Этот алфавит в квадрате Виженера соответствует строке, помеченной буквой Е ключа. Интервалы между повторениями буквы И кратны числу 5. Все три интервала кратны 5.
17 – 12 = 5, 17 – 2 = 15, 12 – 2 = 10.
Аналогично с буквой У в 1 и 11— й позициях ШТ, интервал 11 – 1=10 кратен 5; с буквой Ч в 3-й и в 13-й позициях ШТ; интервал равен 13 – 3 = 10, что также кратно 5. Буква Я в позициях 7-й и 18-й ШТ не удовлетворяет общему правилу 18 – 7=11, что не кратно 5, а вот буква А в ШТ в позициях 5-й и 15-й опять подчинена правилу, интервал 15 – 5 = 10 кратен 5.
Как только решен этот вопрос сразу же становится возможным определение списков букв ШТ, которые были зашифрованы одним и тем же смешанным алфавитом. Не зная самого ключа, мы должны полагать, что используются пять различных алфавитов (по числу букв в ключе), т.е. пять строк квадрата Виженера.
Множество всех букв ШТ теперь можно расчленить на L = 5 групп, таким образом, что в каждой группе соберутся буквы из одной строки квадрата Виженера, т. е. из одного смешанного алфавита. Таким образом удается свести задачу к нескольким последовательным, но одноалфавитной замены для каждого. А это уже задача из числа успешно решаемых. Как же осуществить разбиение букв?
На этом этапе вскрытия шифрограммы перед нами встает задача выбора дальнейшего пути исследования. Если бы выборки в каждой группе были значительными (более 700 букв), то используя закон частоты встречаемости буквы, сопоставив частоту появления букв в русском языке и в каждой группе, а также учитывая семантику вскрываемого текста можно было бы и завершить решение задачи, но при малых выборках ожидать успеха на этом пути не приходится.
Можно ли каким-то образом получить такие матрицы, не располагая данными о ключе?
Эта информация может явиться той основой, которая позволит выявить сам ключ, т.е. слово. Ясно, что, зная величину сдвигов между алфавитами, можно пытаться подобрать слово из букв стандартного алфавита по маске, которая учитывает структуру самих сдвигов. Поиск может выполняться с использованием словарей или с визуальным контролем. Надо полагать, что ключ будет осмысленным словом или даже фразой. Это и должно использоваться при контроле в процессе поиска ключа.
Покажем на нашем примере как такой поиск выполняется. Построим (гребенку (Рис. 1 которая будет играть роль движка или шаблона (маски). Разность между крайними отметками на гребенке равна модулю наибольшего сдвига между алфавитами. Отметим крайние положения (зубцы) гребенки номерами наиболее раздвинутых алфавитов (в примере наиболее удаленных друг от друга букв Т и Е ключа) как 1 и 2. Все другие положения на гребенке определяются относительными расстояниями (сдвигами) алфавитов, занимающих промежуточное положение между выявленными крайними.
Снабдим их соответствующей нумерацией 3, 4, 5. Теперь, если перемещать движок- гребенку вдоль стандартного алфавита, помещенного на полоске, склеенной в кольцо, и считывать буквы напротив зубцов, то оказывается, что различных положений у такого движка всего 32 по числу букв в алфавите. Соответственно и буквенных наборов, потенциально образующих ключ такое же число. Остается выяснить путем перебора какая совокупность букв с точки зрения семантики наиболее подходит в качестве ключа. Считаем, что лента с алфавитом склеена в кольцо и движок перемещается по окружности.
На самом деле вопрос о построении гребенки не так прост. В нашем примере мы знаем ключ и соответственно ему нумеровали рабочие алфавиты из квадрата Виженера. При неизвестном ключе мы можем построить гребенку, но нумерация зубцов остается невыясненной. Порядок букв в ключе (относительный) будет определен так. В примере мы крайний правый зубец гребенки снабдили номером 1, а крайний левый номером 2, что соответствует буквам Т и Е стандартного алфавита. Но, не зная ключа, можно было поместить зубцы и наоборот (зубцы на Рис.1 для второй возможности представлены в виде (“-^-“)
Беглый анализ этих совокупностей после прочтения показывает, что совсем непросто получить осмысленный текст при произвольном выборе гребенки. Даже похожих на осмысленные слова совокупностей практически нет. Первая совокупность могла бы быть подозрительной на ключ с учетом того, что допущена ошибка в длине ключа и ключом является слово НАЕМНИК.
Но среди всей этой абракадабры имеется одно единственное вполне осмысленное слово ТЕКСТ (выделено заливкой) и, конечно, только оно может быть принято в качестве ключа.
Заключение
Материал приведенный в публикации знакомит с простыми шифрами алфавитной замены, которые известны с прошлого столетия или еще раньше, но для тех читателей, которые раньше не были знакомы с проблемами информационной безопасности, текст может быть интересен.
Подробно рассмотрено влияние ключа (его длины и состава) на шифртекст. Упоминание о законах естественного языка, которые всегда учитываются в науке криптология может заинтересовать читателей по разным причинам. Так, например, совсем слабо освещена в науке проблема избыточности ЕЯ. Как от нее избавляться или как ее использовать, где эта избыточность размещается в текстах мало что известно.
Архиваторы, сжимающие тексты, существуют давно, но их теория на сформулированные вопросы не отвечает. Более того, часто архиваторы проектируются так, чтобы тексты восстанавливались без потерь, т.е. исходная избыточность текстов восстанавливается.