как работает регуляризация в решающих деревьях какие параметры мы штрафуем в данных алгоритмах

Регуляризация

Регуляризация необходима для машинного и глубокого обучения. Это не сложный метод и он упрощает процесс машинного обучения. Настройка модели машинного обучения заключается не только в подаче данных. Во время обучения модели на станке с помощью искусственных нейронных сетей Вы столкнетесь с многочисленными проблемами. Эти проблемы могут существенно повлиять на производительность. Эта статья поможет вам разобраться в техниках, которые вы можете использовать для уменьшения количества проблем в процессе обучения работе со станком.

Что такое Регуляризация?

Использование регуляризации – это то же самое, что и название. Регуляризация означает сделать вещи приемлемыми или регулярными. Регуляризация – это техника, которая уменьшает ошибки модели, избегая переоснащения и обучая модель правильному функционированию.

Переподгонка

Переоснащение – обычная проблема. Когда вы переполняете модель данными, которые не содержат возможности обработки, она начинает действовать нерегулярно. Эта нерегулярность будет включать в себя шум, а не сигнал. Ваша модель начнет рассматривать ненужные данные как концепцию. Термин, используемый для обозначения этого, является “переподстройкой”, и это приводит к неточным выводам, что снижает точность и эффективность данных.
Предположим, нам необходимо предсказать, будут ли новоиспеченные студенты допущены к собеседованию. Мы обучим нашу систему 20 000 резюме, чтобы понять, соответствуют ли они квалификационным требованиям или нет. Результат, который мы получим, будет точным на 99 процентов. Теперь, когда вы тестируете свою модель с совершенно другим набором данных, результат будет менее 50 процентов. Это происходит потому, что модель, которую мы тренируем, не обобщает результат по невидимым данным. Мы также видим, что это вписывается в нашу повседневную жизнь.

Шум и сигнал

Сигнал – это шаблон, который помогает модели изучить соответствующие данные. Однако шум – это случайная и несущественная форма данных, которую вы не хотите вовлекать в результат. Мы не хотим, чтобы наши модели включали иррелевантные данные и влияли на наши результаты. Причиной этой нерегулярности является алгоритм модели. Он учит и устраняет ошибки во время тренировочного процесса.
Обучение в течение более длительного периода, даже после устранения всех ошибок, снизит производительность, так как модель начнет изучать неактуальные данные. Это усложнит нашу модель, и она не сможет обобщать новые данные. Хороший алгоритм разделит шум и сигнал.

Как работает регуляризация

Основная причина “переподгонки” модели заключается в том, что она не может обобщить данные из-за слишком большой нерелевантности. Однако регуляризация является эффективным методом, повышающим точность модели и уменьшающим ненужные отклонения.
Кроме того, этот метод позволяет избежать потери важных данных, что происходит с подгонкой. Регуляризация помогает модели учиться, применяя ранее изученные примеры к новым невидимым данным. Также можно уменьшить емкость модели, сводя различные параметры к нулю. Регуляризация удалит дополнительные веса из конкретных характеристик и равномерно распределит эти веса.
Давайте разберемся, как это работает. Когда мы хотим, чтобы модель работала правильно, мы определяем функцию потерь. Эта функция потерь будет определять производительность модели по данным путем расчета потерь. Нам нужно минимизировать потери, чтобы найти нужную модель. Для этого регуляризация добавляет лямбда, чтобы оштрафовать функцию потерь. Мы получаем оптимальное решение от этой методики, так как она отвергает высокие ошибки обучения при меньших значениях лямбда и отвергает более сложные модели с большими значениями лямбда.

Типы техники регуляризации

1. L1 Регуляризация

Регрессионная модель этой техники регуляризации называется регрессией Лассо. Модель регрессии – это штрафной термин. Лассо является кратким для Оператора Наименее Абсолютной Усадки и Выбора. Лассо добавляет абсолютное значение величины к коэффициенту. Эти значения являются штрафными терминами функции потерь.

2. L2 Регуляризация

С другой стороны, регрессионная модель регуляризации L2 – это регрессия гребней. В этой регуляризации штрафным членом функции потерь является квадратная величина коэффициента. В этом методе значение лямбда равно нулю, так как при добавлении большого значения лямбда будет прибавляться больше весов, что приводит к недоустановке.
Выбор между L1 и L2 Регуляризация
Для выбора метода регуляризации между L1 и L2 необходимо учитывать объем данных. Если данные больше, то следует использовать регуляризацию L2. Однако, если данные небольшие, необходимо выбрать регуляризацию L1.

3. Регуляризация выпадения данных

Согласно Википедии, отсев означает отсев видимых или скрытых единиц. Простыми словами, бросить – значит игнорировать юниты или нейроны во время тренировки модели. Модель не будет учитывать эти единицы при передаче данных через искусственную нейронную сеть. Это позволит избежать перегрузки тренировочных данных.

4. Расширение данных

В технике увеличения данных вы увеличиваете размер релевантных данных или сигнала, которые вы хотите включить в выходные данные. Основная причина, по которой модель не является обобщающей, заключается в переподборе. Однако, когда размер соответствующих данных увеличивается, модель не будет рассматривать добавление шума.

Заключение

Когда мы обучаем нашу модель посредством контролируемого обучения работе с машиной, мы передаем данные обучения. Теперь модель будет обучаться через модели тренировочных данных. Мы ожидаем, что модель определяет модели только через сигнал, что является релевантными данными. Однако, модель также включает в себя шум. Это влияет на производительность модели при прохождении новых данных.
В этом помогает техника регуляризации. Она уменьшает сложность, добавляя штраф. Существует два общих типа методов регуляризации. L1 минимизирует значение весов, а L2 минимизирует квадратную величину. Однако есть еще две техники для избежания переподготовки, одна из которых – “выпадание”, а другая – “увеличение данных”. Drop out будет игнорировать не относящиеся к делу единицы или шум, а увеличение данных увеличит размер сигнала.

Источник

Регуляризация

Содержание

Мотивация [ править ]

Как говорилось ранее, регуляризация полезна для борьбы с переобучением. Если вы выбрали сложную модель, и при этом у вас недостаточно данных, то легко можно получить итоговую модель, которая хорошо описывает обучающую выборку, но не обобщается на тестовую.

На примере линейной регрессии [ править ]

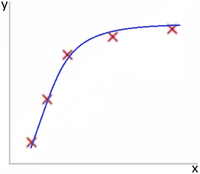
На Рис. 1 представлена зависимость, которая хорошо подходит для описания данных, а на Рис. 2 — модель, слишком сильно заточенная под обучающую выборку.

Однин из способов бороться с негативным эффектом излишнего подстраивания под данные — использование регуляризации, т. е. добавление некоторого штрафа за большие значения коэффициентов у линейной модели. Тем самым запрещаются слишком «резкие» изгибы, и предотвращается переобучение.

На примере логистической регрессии [ править ]

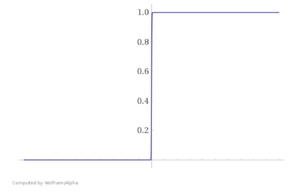
Необходимость регуляризации можно увидеть и на другом примере — при использовании логистической регресии. Представьте, что ваша обучающая выборка была линейно разделима. В таком случае в процессе оптимизации значения весов модели уйдут в бесконечность, и вместо сигмойды получится «ступенька», представленная на Рис. 3.

Это плохо, ибо произошло затачивание под обучающую выборку. Как и в предыдущем примере, побороться с этим можно путем добавления регуляризатора, не дающего весам принимать слишком большие значения.

Основные виды регуляризации [ править ]

В представленных ниже формулах для эмпирического риска [math]Q[/math] : [math]\mathcal[/math] является функцией потерь, а [math]\beta[/math] — вектором параметров [math]g(x, \beta)[/math] из модели алгоритма, а [math]\lambda[/math] — неотрицательный гиперпараметр, являющийся коэффициентом регуляризации.

Запишем задачу настройки вектора параметров [math]\beta[/math] :

где [math]\mathcal_(\beta) = \mathcal(y_, g(x_, \beta))[/math] — некоторая ограниченная гладкая функция потерь. Сделаем замену переменных, чтобы функционал стал гладким. Каждой переменной [math]\beta_[/math] поставим в соответствие две новые неотрицательные переменные:

[math]\begin \beta_ = u_ — v_ \\ |\beta_| = u_ + v_ \end[/math]

В новых переменных функционал становится гладким, но добавляются ограничения-неравенства:

Эластичная сеть [ править ]

Вероятностная интерпретация регуляризации [ править ]

Эквивалентная вероятностная задача [ править ]

Перед нами стоит задача — минимизировать эмпирический риск:

[math]Q(\beta, X^l)=\sum\limits _^l\mathcal(y_, g(x_, \beta)) \rightarrow \min\limits_<\beta>[/math]

[math]p(X^l|\beta)=\prod\limits_^lp(x_,y_|\beta) \rightarrow \max\limits_<\beta>[/math]

Удобнее рассматривать логарифм правдоподобия:

[math]L(\beta, X^l)=\ln p(X^l|\beta)=\sum\limits_^l \ln p(x_, y_|\beta) \rightarrow \max\limits_<\beta>[/math]

Можно заключить, что задачи в исходном и вероятностном представлении эквивалентны, если положить:

[math]-\ln p(x_, y_|\beta)=\mathcal(y_, g(x_, \beta))[/math]

Принцип максимума совместного правдоподобия данных и модели [ править ]

[math]p(X^l, \beta; \gamma)=p(X^l|\beta)p(\beta;\gamma)[/math]

Таким образом, приходим к принципу максимума совместного правдоподобия данных и модели:

[math]L_<\gamma>(\beta, X^l)=\ln p(X^l, \beta;\gamma)=\sum\limits_^l \ln p(x_, y_|\beta) + \ln p(\beta; \gamma) \rightarrow \max\limits_<\beta>[/math]

Функционал [math]L_<\gamma>[/math] распадается на два слагаемых: логарифм правдоподобия и регуляризатор, не зависящий от данных. Второе слагаемое ограничивает вектор параметров модели, не позволяя ему быть каким угодно.

В итоге мы получили, что с байесовской точки зрения многие методы регуляризации соответствуют добавлению некоторых априорных распределений на параметры модели. При этом можно определить распределения, которые соответствуют представленным ранее [math]L_<1>[/math] и [math]L_<2>[/math] регуляризаторам.

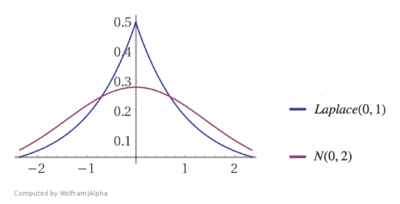
Нормальный регуляризатор [ править ]

[math]\beta \sim N(0, \sigma^2)[/math]

Логарифмируя, получаем квадратичный регуляризатор:

Лапласовский регуляризатор [ править ]

[math]\beta \sim Laplace(0, C)[/math]

Регуляризация в линейной регрессии [ править ]

$g(x, \beta) = \sum\limits_^n \beta_ \,f_(x)$

В итоге оптимизируемый функционал эмпирического риска выглядит следующим образом:

Гребневая регрессия [ править ]

Итоговый минимизируемый функционал с поправкой:

Оценим эффект, который оказывает добавление гребня. Выразим регуляризованное МНК-решение через сингулярное разложение:

Теперь найдём регуляризованную МНК-аппроксимацию целевого вектора y:

Поэтому данный метод называют также сжатие или сокращение весов.

В нерегуляризованном случае:

В случае с гребнем:

Лассо регрессия [ править ]

Итоговый минимизируемый функционал с поправкой:

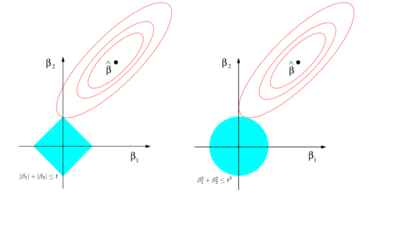
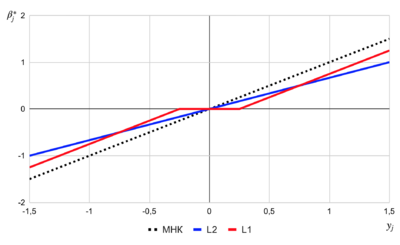
Сравнение гребневой и лассо регрессий [ править ]

В случае с гребневой регрессией:

В случае с лассо регрессией:

$\beta_^* = \begin y_ — \lambda / 2, y_ > \lambda / 2 \\ y_ + \lambda / 2, y_

Регуляризация в алгоритмах [ править ]

Градиентный спуск [ править ]

[math]Q(w, X^l)=\sum\limits_^l\mathcal(y_, \langle w, x_ \rangle) \rightarrow \min\limits_[/math]

где [math]\eta \gt 0[/math] — величина шага в направлении антиградиента.

Регуляризация — одна из эвристик улучшения градиентных методов обучения. Основным способом уменьшить переобучение является квадратичная регуляризация, называемая также сокращением весов. Чтобы ограничить рост абсолютных значений весов, к минимизируемому функционалу [math]Q(w)[/math] добавляется штрафное слагаемое:

Это приводит к появлению аддитивной поправки в градиенте:

[math]Q_<\tau>‘(w) = Q′(w) + \tau w[/math]

В результате правило обновления весов принимает вид:

Регуляризация предовтращает паралич, повышает устойчивость весов в случае мультиколлинеарности, повышает обобщающую способность алгоритма и снижает риск переобучения. Однако есть и недостатки — параметр [math]\tau[/math] необходимо выбирать с помощью кросс-валидации, что связано с большими вычислительными затратами.

Метод опорных векторов [ править ]

Метод опорных векторов (SVM) используется для задач классификации и регрессии. В нем строится гиперплоскость, разделяющая объекты выборки оптимальным образом.

Другие использования регуляризации [ править ]

Логистическая регрессия [ править ]

Как было показано в мотивационном примере, для логистической регрессии может быть полезно использовать регуляризацию.

Аналогично можно использовать и другие регуляризаторы.

Нейронные сети [ править ]

Для нейронной сети помимо добавления штрафного слагаемого к эмпирическому риску активно используют и другой метод борьбы с переобучением — прореживание сети (англ. dropout), в ходе которого упрощают сеть, руководствуясь правилом — если функция ошибки не изменяется, то сеть можно упрощать и дальше. Подробнее об этом можно почитать в статье, рассказывающей о практике реализации нейронных сетей.

Источник

Регуляризация: что это и почему важно

Підписуйтеся на Telegram-канал «DOU #tech», щоб не пропустити нові технічні статті.

Автор: Богдан Цал-Цалко, data scientist в DataRobot, лектор онлайн-школы robot_dreams.

Переобучение часто возникает при попытках улучшения datascience-моделей. Чем больше параметров, тем проще совершить эту ошибку. Я более 8 лет работаю с данными, и знаю, что при создании сложных моделей всегда нужно использовать инструменты, ограничивающие переобучение.

Регуляризация — это один из таких инструментов; своего рода встроенный предохранитель. В материале мы рассмотрим на примере, какова природа переобучения, как регуляризация помогает с ним справиться, а также как ее использовать для линейной регрессии и деревьев принятия решений.

Статья будет полезна аналитикам данных, которые хотят научиться работать с более сложными моделями.

Материал будет легче воспринять тем, кто уже знаком с линейной регрессией. Рассказывать о ней и о других основных типах регрессии я буду на своем курсе «Математика и статистика для анализа данных» в robot_dreams.

В каких случаях нужна регуляризация

Понять, как возникает переобучение, поможет пример.

Допустим, у нас есть ферма по выращиванию рыбы одного вида. Когда мы вылавливаем рыбу, то взвешиваем ее. Также можно допустить, что мы знаем возраст каждой пойманной рыбы. Предположим, что мы хотим оценить зависимость ее веса от возраста. Воспользуемся тем что этот биологический процесс был хорошо исследован, и мы сможем сгенерировать нужные нам данные. Обратимся к формуле роста фон Берталанфи:

а — возраст рыбы (наша единственная фича)

а₀— константа для оценки веса рыбы при рождении (допустим, — 0,47)

k — коэффициент скорости роста (допустим, 0,52)

L_∞— асимптотический вес (допустим, 2,75 кг)

Теперь смоделируем вес рыб в зависимости от возраста с помощью линейной регрессии:

Полученная RMSE (среднеквадратическая ошибка модели) на обучающих данных равна 0,30. Мы специально используем результаты на обучающей выборке, чтобы узнать, какова ее способность противостоять переобучению.

Видим, что зависимость явно не линейная, поэтому мы попробуем добавить полиномиальность в регрессию.

Как видно, с увеличением степени метрика на обучающих данных только растёт. Но если мы посмотрим на график того, что получилось для десятой степени, то поймем, какой ценой алгоритм достиг этих улучшений:

Начиная с возраста 7, по нашим оценкам, у рыб может наблюдаться отрицательный вес. Этот искусственный пример наглядно показывает, как работает переобучение в data science.

В данном случае основные проблемы — множество признаков, зависимых между собой, а также неравномерность их распределения. Такое часто наблюдается в реальных примерах при работе с данными. Но в реальности мы не всегда можем перебрать и оставить только те признаки, которые не позволят модели переобучиться. Давайте рассмотрим механизм, который бы помог предотвратить переобучение.

В чем суть регуляризации

Мы будем «наказывать» модель за избыточную сложность. Тут на помощь приходит регуляризация. Для линейной регрессии её идея проста и универсальна: добавить к оценке качества модели — функции потерь — сумму её собственных коэффициентов

Функция потерь обычной линейной регрессии:

Лассо-регрессия (lasso regression) — линейная регрессия с линейной пенализацией коэффициентов:

Ридж-регрессия (ridge regression) — регрессия с квадратичной пенализацией коэффициентов:

Эластик-нет (elastic net) — комбинация ридж-регрессии и лассо-регрессии:

α — это коэффициент который отвечает за влияние регуляризации.

l_{1 ratio} — коэффициент пропорции двух пенализаций в elastic net

Чтоб понять, как подобрать, нужно учитывать, что при:

α→0 мы получаем обратную линейную регрессию

α→∞ мы получаем среднее вместо регрессии

Технически минимизация таких регрессий немного сложнее — в отличие от обычной регрессии, у них нет прямых решений,. Для их решения часто прибегают к градиентному спуску ( почти нейронная сеть ).

Особенности работы с регуляризацией:

В обычной линейной регрессии единица измерения признака (килограммы или граммы) не имеет значения. Но если в моделях с регуляризацией один из признаков будет измеряться в килограммах, а другой — в граммах, то коэффициенты при них будут по-разному влиять на оптимизацию функции потерь. Соответственно, переменная в граммах может оказаться важнее. Я предпочитаю использовать стандартизацию данных при α не больше, чем стандартное отклонение целевого признака.

Посмотрим на примере рыбной фермы, как бы себя повела линейная регрессия с регуляризацией:

Как видим, для десятой степени нашей полиномиальной регрессии лассо-регуляризация показывает гораздо более применимые результаты.

Для ридж-регрессии получается более гладкая кривая, которая лучше описывает левый край:

Регуляризация для деревьев принятия решений

Регуляризация применима не только к линейной регрессии. Это набор приемов к разным моделям, ограничивающий их в стремлении к переобучению.

В семье моделей на основе деревьев принятия решений одно дерево способно выучить все данные. Это приводит к сильному переобучению. Поэтому стратегии регуляризации для них встроены в большинство популярных пакетов. Эти стратегии часто заключаются в ограничении определенных параметров дерева:

Также для регрессионных деревьев можно настраивать коэффициенты для линейной регуляризации, которые используются в их листах.

Леса деревьев принятия решений — более сложная модель. Для нее настраиваются параметры регуляризации, которые встречаются во многих нейросетях и являются универсальными для большинства итеративных моделей обучения:

Скрывая часть данных от моделей, мы отнимаем у них возможность использовать всю вариативность данных, чтоб выучить их наизусть. Слишком высокий отсев может скрыть искомую зависимость между признаками.

Почему регуляризованные модели работают лучше обычных

В моем опыте работы с платформой автоматического машинного обучения DataRobot ridge-регрессия и elastic net зарекомендовали себя гораздо лучше обычной регрессии.

В проекте по оценке риска нанесенных ущербов мы исследовали влияние разных признаков на результат. Это важно для понимания портфеля рисков, оптимизации количества данных и тарифов для потребителей. В рамках этого проекта elastic net показал один из лучших результатов на валидации, хотя обычная линейная регрессия оказалась гораздо ниже в рейтинге моделей. Благодаря связи elastic net с линейной регрессией он предоставил одну из самых простых интерпретаций влияния признаков для компании-заказчика.

Регуляризация — это защитный механизм алгоритмов обучения от избыточной сложности. Он помогает избежать переобучения. Это понятие объединяет множество инструментов и стратегий, и цель их всех — помочь автоматизировать войну data science против переобучения.

Источник

Русские Блоги

Регуляризация машинного обучения (Regularization)

1. The Problem of Overfitting

1

Давайте посмотрим на этот пример прогнозирования цен на дома. Давайте сделаем линейную регрессию на данных, которая является первой картинкой слева.

Если мы сделаем это, мы можем получить такую ​​прямую линию, которая соответствует данным, но на самом деле это не очень хорошая модель. Глядя на эти данные, становится ясно, что по мере того, как увеличивается площадь дома, изменение цен на жилье имеет тенденцию быть стабильным, или чем больше прав, тем более постепенным. Следовательно, линейная регрессия не очень хорошо подходит для тренировочных данных.

Мы называем этот тип подгонки, или высокий уклон.

На втором рисунке мы добавляем квадратный член в середине, что означает, что мы используем квадратичную функцию, чтобы соответствовать этим данным. Естественно, можно подобрать кривую, и факты доказали, что этот эффект подгонки очень хорош.

С другой стороны, если многочлен четвертой степени подгоняется к набору данных на третьем графике. Итак, здесь у нас есть пять параметров от θ0 до θ4, так что мы также можем подогнать кривую, и через наши пять обучающих выборок мы можем получить кривую, подобную той, что справа.

С одной стороны, мы, кажется, хорошо подходим к тренировочным данным, потому что эта кривая проходит все обучающие примеры. Тем не менее, это на самом деле очень искаженная кривая, она продолжает колебаться вверх и вниз. Поэтому, на самом деле, мы не думаем, что это хорошая модель для прогнозирования цен на жилье.

Поэтому мы называем подобную ситуацию переоснащением, также называемой высокой дисперсией.

То же, что и высокое отклонение, Высокая дисперсия также является историческим термином. На первый взгляд, если мы подберем многочлен высокого порядка, то эта функция может хорошо соответствовать обучающему набору (может соответствовать почти всем обучающим данным), но это также сталкивается с проблемой, что функция может быть слишком большой Слишком много переменных.

В то же время, если у нас недостаточно набора данных (обучающего набора), чтобы ограничить эту модель слишком большим количеством переменных, произойдет переобучение.

2

Проблема переобучения обычно возникает, когда имеется слишком много переменных (функций). В этом случае уравнение обучения всегда может очень хорошо соответствовать обучающим данным, то есть наша функция стоимости может быть очень близка к 0 или нулю.

Однако такая кривая делает все возможное, чтобы соответствовать обучающим данным, что приведет к невозможности обобщения для новых выборок данных, так что невозможно предсказать цену новой выборки. Здесь, Термин «обобщение» относится к способности гипотетической модели применяться к новым выборкам. Новые примеры данных относятся к данным, которые не отображаются в обучающем наборе.

Ранее мы видели переоснащение в случае линейной регрессии. Аналогичная ситуация относится к логистической регрессии.

3

Итак, если возникает проблема с переоснащением, что нам делать?

Слишком много переменных (функций) и очень мало данных обучения одновременно могут вызвать проблемы с переобучением. Поэтому, чтобы решить проблему переоснащения, существуют следующие два метода.

Способ 1. Попробуйте уменьшить количество выбранных переменных

В частности, мы можем вручную проверить каждую переменную и использовать ее, чтобы определить, какие переменные являются более важными, а затем сохранить эти более важные переменные функции. Что касается того, какие переменные должны быть отброшены, мы обсудим позже, это будет включать алгоритм выбора модели, этот алгоритм может автоматически выбирать, какие переменные функции принять, и автоматически отбрасывать ненужные переменные. Этот тип подхода очень эффективен, но его недостатком является то, что когда вы отбрасываете некоторые переменные функции, вы также отбрасываете некоторую информацию в вопросе. Например, возможно, все характерные переменные полезны для прогнозирования цен на жилье.На самом деле мы не хотим отбрасывать некоторую информацию или эти характерные переменные.

Метод 2: Регуляризация

При регуляризации мы сохраним все характеристические переменные, но уменьшим порядок характерных переменных (размер значения параметра θ (j)).

Этот метод очень эффективен. Когда у нас много характерных переменных, каждая из них может оказать небольшое влияние на прогноз. Как мы видели в примере прогнозирования цен на жилье, у нас может быть много характерных переменных, каждая из которых полезна, поэтому мы не хотим удалять их, что приводит к концепции регуляризации.

Далее мы обсудим, как применять регуляризацию и что называется регуляризованным средним, а затем мы начнем обсуждать, как использовать регуляризацию для правильной работы алгоритма обучения и избежания переобучения.

2. Cost Function

1

В предыдущем введении мы видели, что если для подгонки этих данных используется квадратичная функция, то она дает нам хорошее соответствие для данных. Однако, если мы используем полином более высокой степени для подгонки, у нас может получиться кривая, которая хорошо соответствует обучающему набору, но это не очень хороший результат, потому что он перекрывает данные, Поэтому общность не очень хорошая.

Давайте рассмотрим следующее предположение, которое мы хотим добавитьШтрафы, Так что параметры θ3 и θ4 достаточно малы.

Я имею в виду, что приведенная выше формула является нашей целью оптимизации, а это означает, что нам нужно минимизировать среднеквадратичную ошибку функции стоимости.

Для этой функции мы добавим несколько терминов, добавим 1000 раз квадрат 3 и добавим 1000 раз квадрат 4,

Таким образом, мы наконец подгоняем данные должным образом. То, что мы используем, это квадратичная функция плюс некоторый очень маленький, маленький вклад (потому что θ3 и θ4 этих членов очень близки к 0). Очевидно, это лучшее предположение.

2

В более общем смысле, вот идея регуляризации. Идея состоит в том, что если наше значение параметра соответствует меньшему значению (значение параметра меньше), то мы часто получаем более простое предположение.

В нашем примере выше мы штрафовали только 3 и 4, так что эти два значения близки к нулю, поэтому мы получаем более простое предположение, которое на самом деле является квадратичной функцией.

Но в более общем плане, если мы накажем другие параметры, такие как θ3 и θ4, то мы часто можем получить относительно простое предположение.

Фактически, чем меньше значение этих параметров, обычно соответствует более гладкой функции, то есть более простой функции. Поэтому проблема переоснащения вряд ли возникнет.

Я знаю, почему меньший параметр соответствует относительно простому предположению, которое вы, возможно, не до конца поняли, но в приведенном выше примере уменьшение θ3 и θ4 может сделать нас проще Предположим, этот пример, по крайней мере, дает нам некоторые интуитивные чувства.

Давайте посмотрим на конкретные примеры. У нас могут быть сотни характеристик для прогнозирования цен на жилье. В отличие от только что упомянутого полиномиального примера, мы не знаем, что θ3 и θ4 являются терминами полиномов высшего порядка. Итак, если у нас есть сотня функций, мы не знаем, как выбрать параметры с лучшей корреляцией, как уменьшить количество параметров и так далее.

Поэтому нам нужно изменить функцию стоимости и добавить элемент после этого, как мы это делали в квадратных скобках. Когда мы добавляем дополнительный термин регуляризации, мы сокращаем каждый параметр.

Кстати, по соглашению, мы не оштрафовали θ0, поэтому значение θ0 велико. Это сумма от 1 до n, а не от 0 до n. Но на практике
Это будет иметь очень небольшое значение, независимо от того, используете ли вы это θ0 или нет. Но согласно соглашению, мы обычно только регуляризуем от θ1 до θn.

Следующий пункт является термином регуляризации

и λ здесь называется параметром регуляризации.

λ Все, что вам нужно сделать, это контролировать баланс между двумя разными целями.

Первая цель состоит в том, что мы хотим тренироваться так, чтобы гипотеза лучше соответствовала тренировочным данным.Мы надеемся, что предположение может быть хорошо адаптировано к тренировочному набору.

Тем не менее, параметр регуляризации λ должен управлять балансом между этими двумя показателями, то есть целью сбалансированной тренировки подгонки и целью поддержания малого значения параметра. Чтобы сохранить гипотетическую форму относительно простой, чтобы избежать переоснащения.

Для нашего прогноза цен на жилье мы использовали очень многочлен высокого порядка, мы получим очень кривую и сложную функцию кривой, теперь нам нужно только использовать целевой метод регуляризации, затем вы Можно получить более подходящую кривую, но эта кривая не является реальной квадратичной функцией, а более гладкой и простой кривой. Это дает нам лучшее предположение для этих данных.

Еще раз, эту часть контента действительно трудно понять, почему эффект добавления параметров может иметь такой эффект? Но если вы лично оформите это, вы сможете увидеть самые интуитивные ощущения этого эффекта.

3

Что произойдет в случае регуляризованной линейной регрессии, если значение параметра регуляризации очень большое?

Если мы сделаем это, то наша гипотеза будет эквивалентна удалению этих терминов и оставлению нас только с простой гипотезой, которая может только показать, что цена дома равна значению θ0, что аналогично подгонке Горизонтальная линия является недостаточным для данных. В этом случае предполагается, что это прямая линия, которая терпит неудачу. Для обучающего набора это просто плавная линия. У нее нет тенденции, и она не будет стремиться к значению большинства обучающих выборок.

Другой способ выразить это предложение состоит в том, что в этом допущении слишком сильное «предубеждение» или слишком высокое отклонение (bais), и что прогнозируемая цена равна только 0. Для данных это просто горизонтальная линия.

Поэтому, чтобы регуляризация работала хорошо, мы должны обратить внимание на некоторые аспекты, мы должны выбрать хороший параметр регуляризации λ. Когда мы будем говорить о множественном выборе в будущем, мы обсудим метод автоматического выбора параметра регуляризации λ. Чтобы использовать регуляризацию, мы применим эти понятия к линейной регрессии и логистической регрессии. Затем мы можем сделать Они избегают переоснащения.

3. Regularized Linear Regression

Как мы уже упоминали ранее, функция стоимости регрессии гребня выглядит следующим образом:

Для линейной регрессии мы использовали два алгоритма обучения, один на основе градиентного спуска и один на основе нормальных уравнений.

1

Градиентный спуск, следующим образом:

2

Нормальное уравнение выглядит следующим образом:

3

Теперь рассмотрим M (то есть размер выборки), который меньше или равен N (то есть количеству признаков).

К счастью, регуляризация также решает эту проблему для нас, в частности, если регулярные параметры строго больше нуля, мы можем доказать следующую матрицу:

Будет обратимым. Следовательно, регулярное использование может также позаботиться о любых необратимых проблемах XTX.

Итак, теперь вы знаете, как реализовать регрессию гребня. С ее помощью вы можете избежать переоснащения, даже если у вас много функций в относительно небольшом тренировочном наборе. Это должно позволить вам лучше использовать линейную регрессию для многих задач.

В следующем видео мы применим эту идею регуляризации к логистической регрессии, чтобы мы могли предотвратить перегрузку логистической регрессии и повысить ее эффективность.

4. Regularized Logistic Regression

Регуляризованная логистическая регрессия на самом деле очень похожа на регуляризованную линейную регрессию.

Также используйте градиентный спуск:

Если вы используете методы регуляризации в продвинутых алгоритмах оптимизации, то вам необходимо определить costFunction для таких алгоритмов.

For those methods what we needed to do was to define the function that’s called the cost function.

На вход нашей пользовательской функции costFunction входит вектор θ, а возвращаемое значение имеет два элемента, а именно функцию стоимости jVal и градиент градиента.

Короче говоря, нам нужна эта пользовательская функция costFunction. Для Octave мы можем передать эту функцию в качестве параметра системной функции fminunc (fminunc используется для нахождения минимального значения функции, а @costFunction используется в качестве параметра, обратите внимание на @ costFunction аналогичен указателю функции на языке C), fminunc возвращает минимальное значение функции costFunction при неограниченных условиях, то есть минимальное значение функции стоимости jVal, которое мы предоставляем, конечно, оно также будет возвращать решение вектора θ.

Источник