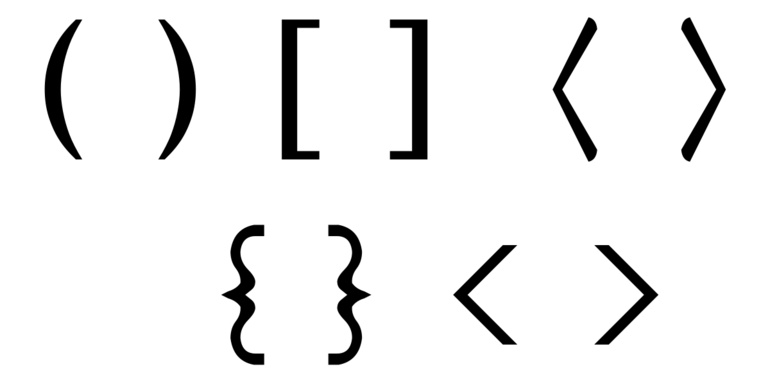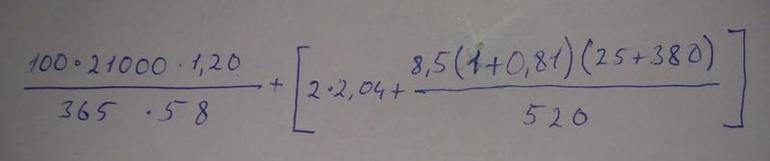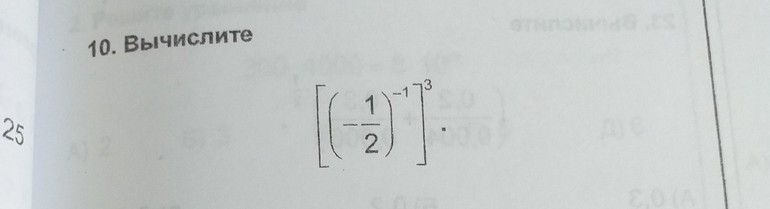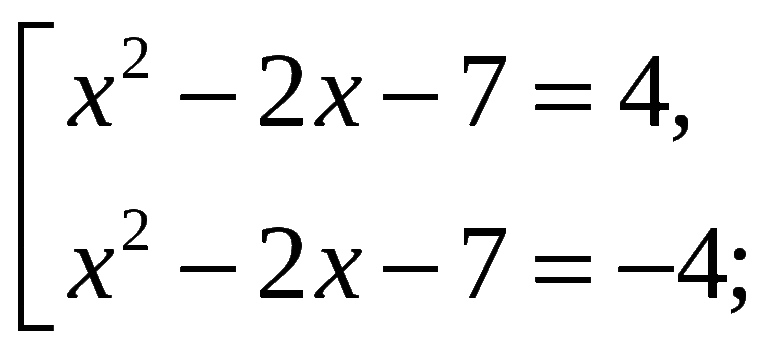как понять какие скобки ставить круглые или квадратные
Запись промежутков. Прием репетитора по математике для запоминания скобок
Н е задавали ли Вам когда-нибудь ученики вопросов, о том, кто впервые придумал те или иные знаки и обозначения? И почему они именно такие. Все репетиторы по математике не раз проверяли и записывали ответы в квадратных и линейных неравенствах. Не раз объясняли школьнику, в чем состоит разница между постановкой квадратной и круглой скобки в обозначении промежутков. Но, как показал опыт общения с преподавателями, далеко не все используют в своей работе аналогии особенностей записи математических объектов во благо запоминания их смысла. Репетитор, как мне кажется, должен уметь работать со всеми видами памяти ребенка, к числу которых относят ассоциативную память. Что я имею ввиду и причем здесь скобки?
Восприятия учеником нового материала имеет одну важную особенность: внимание к отдельным его частям оказывается сильно рассеянным, если репетитор по математике не связывает их с каким-нибудь естественным, понятным, знакомым и интересным процессом / объектом. То есть вызывает ассоциации. Проблема повышения внимания при изучении нового материала заключается в том, что ребенок не знает, какие его части нужно постараться запомнить и понять в первую очередь, ибо не понимает, какой стороной к нему в будущем повернется изучаемый объект. Действительно, откуда ему знать о применении арксинусов и арккосинусов в для записи формул корней тригонометрических уравнений? Может ли он представить себе, что промежутки, которые он проходит с репетитором по математике в 8 классе, берут в оборот буквально все темы вплоть до 11 класса? Откуда он знает, что именно придется повторять при подготовке к ЕГЭ? Репетитору совсем не просто фокусировать внимание школьника на простом факте или записи, которым в программе не уделяется должного внимания в момент их введения.
Покажу прием, который я использую для обоснования и запоминания логики постановки скобки для записи границы числового промежутка.
Какую аналогию использует репетитор по математике?
Обозначение часто отражает характер рассматриваемого объекта и таким образом помогает запоминанию. Если число включается во множество, то его надо «удержать», а если исключается, то «выпустить». Нечто похожее происходит с шариком на круглой и прямой полочке. Если полку сделать правильной, то есть прямой, и положить на нее шарик, то он на ней и останется. Именно так изображается квадратная скобка. Как показать ученику? Репетитор по математике рисует шарик как показано на рисунке

Забавное наблюдение, не правда ли? Практика моей работы говорит о том, что дети с большим интересом воспринимают любые эффектные объяснения, которые резко поднимают эмоциональный настрой. Если репетитор по математике проведет аналогию полочек, ученик запомнит назначение скобки. Станет понятно, что ее выбор зависит от того, хотим ли мы оставить число во множестве или нет.
Разница между скатившимся и удержанным шариком весьма значительная и поэтому прочное запоминание правила гарантировано. Практика показывает, что даже очень слабые дети, для которых подготовка к ЕГЭ по математике оказывается делом неимоверно сложным и тягостным, уверенно ставят на экзамене нужную скобку без каких-либо подсказок репетитора. Для обеспечения прочного запоминания репетитору по математике достаточно напомнить о полочках и шарике пару раз в течение последующих уроков.
Можно было потратить уйму времени на чтение исторической математической литературы и не найти ссылок на подобные наблюдения. Многие общепринятые в современной математике обозначения люди отбирали из множества других форм так, чтобы эти обозначения говорили о тех или иных свойствах объектов. Репетитору не мешало бы использовать их в методике объяснений. Дети часто путают скобки, ибо не понимают смысла, который в них вкладывается.
Уважаемые репетиторы и школьные преподаватели, обращайте внимание на разные мелочи, которых в такой науке как математика существует огромное множество. Учитесь их находить! Проявляйте наблюдательность и фантазию. Тогда многие процессы, о которых никак не удается рассказать ученику, предстанут перед его глазами более открытыми, простыми и интересными. Знак бесконечности, например, можно объяснить тем, что по восьмерке можно крутиться бесконечно, а знак 0, по которому тоже можно водить карандаш без остановки, — уже занят для записи соответствующего числа. Понимание логики оформления ответов является крайне важным для усвоения любого материала. Если это произойдет на ранней стадии обучения, то подготовка к ЕГЭ по математике не вызовет у ученика ни отвращения ни беспокойства.
Колпаков А.Н. Репетитор по математике. Автор идеи шарика.
Спасибо за Вашу работу, очень интересный прием. Здесь и запоминание и понятие. Слабым ученикам я говорю, что знак нестрогого неравенства состоит из трех отрезков, и их можно сложить в квадратную скобку, а знак строгого можно превратить в дугу. Но, конечно, это для очень слабых, к сожалению, таких все больше. С уважением. Н.М.
Здравствуйте, Надежда Михайловна. С тремя палочками от нестрогого неравенства — СУПЕР! Сам возьму на вооружение. Чего только не откроешь нового и неожиданного в общении с наблюдательными репетиторами по математике, учителями школ, учениками. А вот на счет строгого знака — сомнительная аналогия. Вот если бы знаком
Как записать ответ неравенства
Впрочем, мы рекомендуем освоить запись ответа неравенства в математических обозначениях сразу, так как в любом случае в старшей школе и затем в университете будут требовать именно такую запись ответа.
Перед разбором, как записывать ответ неравенства математическими знаками, вспомним расшифровку и обозначение этих знаков.
| Знак | Расшифровка |
|---|---|
| ∈ | «Принадлежит» Легко запомнить знак, как зеркальное отображение русской буквы « Э » или как символ евро « € », но только с одной палочкой посередине. |
| ( … ) | «Круглые скобки» Используются, когда число на границе интервала НЕ входит в сам интервал. На числовой оси такие числа обозначают «пустой» точкой. |
| [ … ] | «Квадратные скобки» Используются, когда число на границе интервала входит в сам интервал. На числовой оси такие числа обозначают «заполненной» точкой. |
| ∪ | «Объединение» Знак похож на подковку. Используется для объединения двух и более интервалов. |
| + ∞ | «Плюс бесконечность» Изображается как цифра « 8 » на боку со знаком « + » слева. Обозначает бесконечность на положительном (правом) краю числовой оси. |
| − ∞ | «Минус бесконечность» Изображается как цифра « 8 » на боку со знаком « − » слева. Обозначает бесконечность на отрицательном (левом) краю числовой оси. |
Перейдем к непосредственной записи ответа неравенства. Рассмотрим и решим линейное неравенство.
Мы решили линейное неравенство, теперь запишем его ответ с помощью математических знаков.
Перед тем, как записывать ответ неравенства, обязательно изобразите его на числовой оси.
Итак, мы изобразили ответ неравенства на числовой оси. После этого запишем слово «Ответ:» и за ним запишем « x ∈ ». Такая запись читается как «икс принадлежит».
Взглянув на рисунок ответа на числовой оси, мы видим, что область решений начинается с числа « 14 ». Число « 14 » не входит в область решений («пустая» точка на оси). Значит, используем круглую скобку.
Нам остается понять, где заканчивается область решений справа. Правильный ответ — справа область заканчивается в положительной бесконечности « + ∞ ».
На числовой оси на обоях краях слева и справа соответственно расположены «минус» и «плюс» бесконечности. Как правило, их не рисуют на числовой оси лишний раз, т.к. их наличие на оси подразумевается.
Запишем окончательный ответ.
Знаки « + ∞ » и « − ∞ » всегда записываются с круглыми скобками.
Разберем другой пример.
Также как и в предыдущем примере всегда начинаем записывать
ответ с записи « x ∈… ».
В ответе « x ≤ 8 » область решений начинается с « − ∞ » и заканчивается на « 8 », которое входит в ответ. Значит, « 8 » будет с квадратной скобкой. Так и запишем в ответе.
Запись ответа неравенства для квадратных неравенств
При решении квадратных неравенств часто может получаться несколько интервалов в ответе. Разберемся, как их записывать в ответ. Рассмотрим пример квадратного неравенства и его решение.
x 2 − 3x + 2 3 2 − 4 · 1 · 2
x1;2 =
| 3 ± √ 9 − 8 |
| 2 |
Рассмотрим другой пример квадратного неравенства и его решения.
x1;2 =
| 2 ± √ 2 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| 2 ± √ 4 + 12 |
| 2 |
В ответе неравенства мы получили два интервала в области решений
(x ≤ −1; x ≥ 3) и оба интервала нужно записать в ответ. Запись ответа неравенства всегда делается слева направо (как мы привыкли читать).
Начнем слева направо записывать интервалы в ответ. Первый интервал начинается с «минус» бесконечности и заканчивается на « −1 » (включительно). Так и запишем.
Второй интервал начинается с « 2 »(включительно) и заканчивается на «плюс» бесконечности. Для объединения интервалов используем знак « ∪ » («объединение»).
Скобки в математике
Вы будете перенаправлены на Автор24
Скобки в математике играют очень важную роль: с помощью них задаётся порядок действий с выражением, обозначаются границы промежутков и необходимость выполнения какого-либо действия над выражением. Также с помощью скобок обозначаются вектора и матрицы и действия с множествами.
Использование круглых скобок в математике
Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.
Первое применение.
С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.
В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.
Второе применение.
Третье применение.
Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.
$(x+2)^2; \int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$
Четвёртое применение.
Пятое применение.
Готовые работы на аналогичную тему
Пятое применение.
Квадратные скобки в математике
Что же означают квадратные скобки в математике и для чего они используются?
Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.
Первое применение.
Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.
Второе применение.
Третье применение.
С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.
$\left [ \begin
Фигурная скобка в математике
Первое применение.
С помощью символа фигурной скобки обозначают систему уравнений, решением которой являются корни, подходящие для всех уравнений, включённых в систему.
Второе применение.
Третье применение.
Треугольные скобки
В чем разница между круглыми и квадратными скобками?
В скобках прописываются промежутки, в каких функция существует, то есть имеет решение. Круглая скобка означает, что число не входит в область определения, квадратная – входит. При наличии бесконечности принято изображать круглую скобку.
Какая разница между круглыми и квадратными скобками?
Скобки для обозначения числовых промежутков
Для обозначения числовых промежутков используются пары скобок четырех видов: ( ), ( ], [ ) и [ ]. … Круглая скобка, прилегающая к числу, означает, что это число не включено в промежуток, а квадратная – что число включено.
Когда ставятся квадратные скобки в русском языке?
Квадратные скобки ставятся для обозначения главного предложения, круглые для обозначения придаточного предложения. Квадратные скобки используются в простых предложениях для обозначения границ. Круглые также нужны для обозначения вводных предложений.
Что за квадратные скобки?
В этом примере квадратные скобки означают тоже самое, что круглые. А иногда еще бывают скобки внутри скобок, которые тоже внутри скобок. Тогда самые внутренние скобки пишут круглые, средние квадратные, а внешние – фигурные. … Во 2 случае намного понятнее, какая скобка к чему относится.
Что означают квадратные скобки в графике?
В Паскале квадратные скобки используются для записи индексов элементов массива. В выражениях можно использовать только круглые скобки. На всякий случай, знаки операций между величинами тоже пропускать нельзя.
Когда ставятся квадратные скобки а когда круглые?
Если речь идет о числовых промежутках, то квадратные скобки ставятся тогда, когда число входит в числовой промежуток (точка закрашенная). Например: [7; 8]. В этом промежутке есть все числа от 7 до 8, а также сами числа 7 и 8. Круглые скобки ставятся тогда, когда число не входит в промежуток (выколотая точка).
Какие бывают скобки?
Когда ставят двойные скобки?
Двойные скобки и кавычки Если вам надо поставить в кавычки или взять в скобки часть выражения, уже стоящего в кавычках/скобках, запомните два простых принципа двойных скобок и двойных кавычек: … В таком случае читатель точно поймет, где заканчивается одно выражение в скобках/кавычках и как оно соотносится с другим.
Что означают эти скобки?
Скобка в конце сообщения обычно придаёт всему сообщению соответствующий тон. Скобка «)» указывает на позитивный или весёлый тон сообщения, а скобка «(» — на негативный, грустный или печальный тон.
Что означает скобка в интернете?
Что означают скобки в переписке в интернете. … На сайте Большой Вопрос употребление смайликов не привествуется администрацией и модераторами, но умеренное количество скобок не возбраняется. Чем искать смайл, быстрее получается скобочку поставить. Скобочка вот такая ) выражает радость, улыбку.
Где найти квадратные скобки на клавиатуре?
Для открывающей квадратной скобки в русской клавиатуре используются клавиши [х] для открывающей и [ъ] для закрывающей при включенной английской раскладке. C использованием одновременно нажатой клавиши [Shift] на этих же клавишах вы получите фигурные скобки <>.
Как определить какие скобки будут в неравенстве?
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка: Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, Читайте также Как правильно принимать амоксиклав?
Что означают квадратные скобки в формулах по физике?
, а квадратные скобки обозначают целую часть частного от деления m на p (так, ).
Когда нужно ставить скобки?
Этот знак препинания является рекомендованным, может заменяться запятыми или тире. Скобки ставят, если надо уточнить значение отдельных слов, дать попутное указание, разъясняющее смысл фразы, или вставить замечание, дополняющее высказывание.
Какие скобки ставить в функции?
Как найти область определения функции?
Область определения функции с корнем
Функцию с корнем можно определить так: y = n√x, где n — натуральное число больше единицы. Рассмотрим две вариации такой функции. Значит, область определения каждой из функций y = √x, y = 4√x, y = 6√x,… есть числовое множество [0, +∞).
Общая характеристика
Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Значение и разновидности
Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.
В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.
Разновидности:
Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.
В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.
Основные цели квадратной скобки в математике:
Другие варианты расчета:
Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.
Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.
Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.
На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.
Одинарные или двойные выражения
Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.
В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.
Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.
По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.
В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.
В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).
Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0
Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.
Прочие знаки
Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.
Удобство записи системы уравнений
Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.