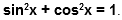как определить в какой четверти находится число
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| \(\frac<\pi><6>\) | \(\frac<\pi><4>\) | \(\frac<\pi><3>\) | \(\frac<\pi><2>\) | \(\frac<2\pi><3>\) | \(\frac<3\pi><4>\) | \(\frac<5\pi><6>\) | \(\pi\) | \(\frac<3\pi><2>\) | \(2\pi\) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
| Отметим на числовой окружности точки, соответствующие \(\frac<\pi><6>,\ \frac<13\pi><6>,\ \frac<25\pi><6>\), и \(-\frac<11\pi><6>\). Все четыре точки совпадают, т.к. \begin  |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: \begin
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: \(-\frac<\pi><2>;\ \frac<3\pi><4>;\ \frac<7\pi><6>;\ \frac<7\pi><4>\).
Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. \begin  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: \(-\frac<11\pi><2>;\ 5\pi;\ \frac<17\pi><6>;\ \frac<27\pi><4>\).
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 | Сравниваем каждое число с границами четвертей: \begin |
\(\frac\pi2\lt 2\lt \pi \Rightarrow \) угол 2 радиана находится во 2-й четверти
\(\pi\lt 4\lt \frac<3\pi> <2>\Rightarrow \) угол 4 радиана находится в 3-й четверти
\(\frac<3\pi><2>\lt 5\lt 2\pi \Rightarrow \) угол 5 радиана находится в 4-й четверти
\(7\gt 2\pi\), отнимаем полный оборот: \(0\lt 7-2\pi\lt \frac\pi2\Rightarrow\) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек \((k\in\mathbb
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
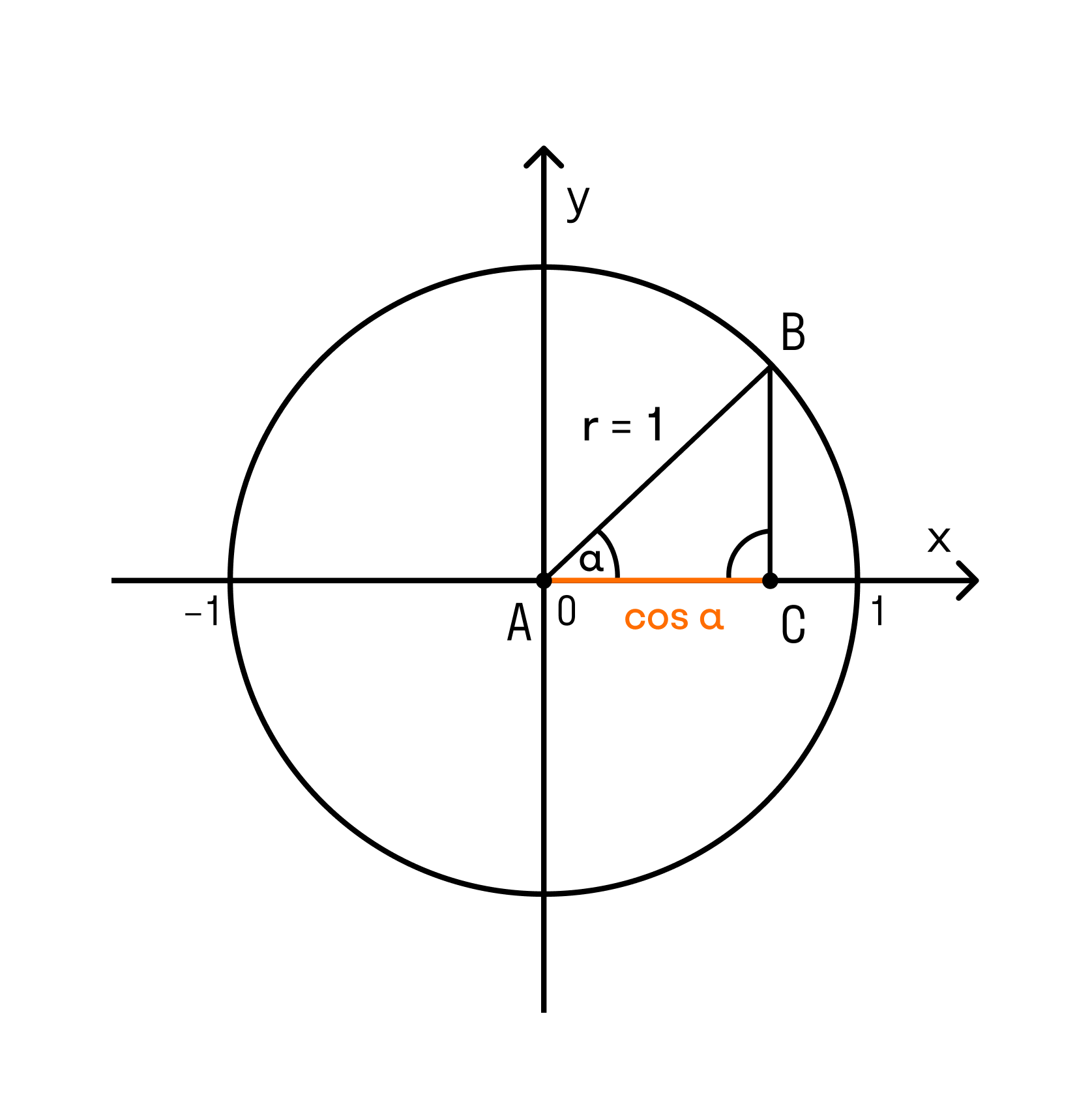
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
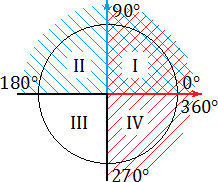
Знаки тригонометрических функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.
Задача. Найдите sin α, если sin 2 α = 0,64 и α ∈ [π/2; π].
Поскольку sin 2 α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.
Задача. Найдите cos α, если cos 2 α = 0,04 и α ∈ [π; 3π/2].
Действуем аналогично, т.е. извлекаем квадратный корень: cos 2 α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.
Задача. Найдите sin α, если sin 2 α = 0,25 и α ∈ [3π/2; 2π].
Имеем: sin 2 α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.
Задача. Найдите tg α, если tg 2 α = 9 и α ∈ [0; π/2].
Все то же самое, только для тангенса. Извлекаем квадратный корень: tg 2 α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!
Единичная окружность
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Для чего использовать единичную окружность
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Тригонометрическая окружность (ЕГЭ 2022)
Привет! Сегодня я научу тебя делать универсальную шпаргалку по тригонометрии, которая называется тригонометрическая окружность.
Если ты поймешь, что такое тригонометрическая окружность, то вся дальнейшая тригонометрия тебе покажется не более чем легкой прогулкой.
Открою секрет: с помощью окружности даже можно решать уравнения и неравенства!
Итак, давай приступим.
Тригонометрическая окружность — коротко о главном
Главный инструмент тригонометрии — это тригонометрическая окружность, она позволяет измерять углы, находить их синусы, косинусы и прочее.
Есть два способа измерять углы:
\( \displaystyle 180<>^\circ =\pi
Чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:
И наоборот: от радиан к градусам:
\( \displaystyle y=sin\ \alpha \)
\( \displaystyle x=cos\ \alpha \)
Чтобы найти синус и косинус угла, нужно:
Формулы приведения:
Это формулы, позволяющие упростить сложные выражения тригонометрической функции.
Эти формулы помогут тебе не запоминать вот такую таблицу:
Что нужно повторить
Вот, что тебе нужно повторить, если ты это забыл:
Вот картинка, которая кратко напомнит тебе, что такое эти синусы, косинусы и т. д.
Также давай вспомним основные соотношения между синусами, косинусами, тангенсами одного и второго острых углов прямоугольного треугольника:
Синус одного острого угла равен косинусу другого (и наоборот), тангенс одного острого угла равен котангенсу другого (и наоборот).
Данные утверждения были доказаны в других статьях. Мы же здесь с тобой уже будем почивать на лаврах, пожиная эти плоды.
Построение тригонометрической окружности
А теперь сделай вот что: возьми-ка в руки циркуль и нарисуй любую (самую любую, но лучше достаточно немаленькую) окружность.
Ну да ладно, задачка не самая сложная. Так, ты не потерял ту точку, в которой у тебя был центр (куда ты прикладывал острую ножку циркуля)? Я вот у себя потерял, растяпа! Ну ладно, найду!
А что пока делать тебе?
А вот что: проведи через эту точку две линии, которые пересекаются «прямым крестиком», то есть под прямым углом. И пусть их точка пересечения – это центр (который ты не потерял!) окружности.
Нарисовал? У меня получилось что-то вроде вот этого.
Правда я чуть-чуть поторопился и сразу «обозвал» эти прямые \( \displaystyle x\) и \( \displaystyle y\) и точку пересечения через \( \displaystyle O\).
А что такое в таком случае \( \displaystyle R\)?
Это радиус нашей окружности.
Как называлась наша тема? Единичная окружность.
Тогда будем считать ( но не будем так рисовать!), что \( \displaystyle R=1\ \).
А рисовать мы так не будем, потому что на такой крошечной картинке ты ничего не разберешь! Ты же понимаешь, что когда инженеры проектируют самолеты, скажем, они не рисуют его в натуральную величину?
Так и мы не будем рисовать единичную окружность в самом деле единичной. Это нам нужно исключительно для удобства.
Теперь отмечаем: \( \displaystyle OR=1\). Что же мы с тобой на самом деле сделали? А вот что:
Мы поместили нашу окружность в систему координат \( \displaystyle \mathbf
Это позволит изучать свойства такой окружности уже не с геометрической, а с математической точки зрения. Этот подход был придуман хитрым математиком и философом Рене Декартом еще в 17 веке!
Перегнать фигуру в цифры, каково, а?
Но допустим, мы поместили нашу окружность в координаты. В скольких точках она пересекается с осями системы координат?
Эти точки \( \displaystyle \left( A;\ B;\ C;\ D \right)\) имеют координаты:
Теперь вспомни, как называются области, на которые этот «координатный крестик» делит всю плоскость?
Они называются координатные четверти.
Тогда посмотри на рисунок. Наша окружность тоже оказалась разрезанной на 4 равные дольки. Давай пронумеруем каждую из этих долек против часовой стрелки:
Ты уже можешь догадаться, как называются эти самые дольки:
1 четверть, 2 четверть, 3 четверть, 4 четверть
(Прямо как четверти в школе!)
Углы на тригонометрической окружности
Теперь давай сделаем еще вот что. Снова посмотрим на предыдущую картинку.
Чему на ней равен \( \displaystyle \angle AOB\)?
Он равен \( \displaystyle 90<>^\circ \).
Также, как и \( \displaystyle \angle BOC\), как и угол \( \displaystyle \angle COD\), и угол \( \displaystyle \angle DOA\).
\( \displaystyle \angle \text
Тогда чему равна их сумма?
Она равна \( \displaystyle 360<>^\circ \).
Вместе же эти 4 угла составляют всю окружность целиком!
Градусная мера окружности равна \( \displaystyle 360<>^\circ \)!
\( \displaystyle \angle A\text
Что еще можно вытянуть? А вот что:
\( \displaystyle \angle A\text
Отметим эти значения также на нашей окружности:
Однако, ты нередко можешь увидеть и вот такую картинку:
где вместо привычных нам градусов появляются некие буковки «пи» \( \displaystyle \pi \) с цифрами.
В чем же тут дело, кто прав и кто виноват?
Ну так вот, кто прав, кто виноват, решать, увы, не нам. Но чтобы «воз не был поныне там», нам нужно уделить этому моменту пару минут времени.
В самом деле, есть два способа измерять углы:
Как измерять углы через градусы мы все знаем. Это нам привычно. Однако в некоторых случаях их измеряют по-другому (как в градуснике есть несколько шкал: цельсий, кельвин, фаренгейт и т. д.), а именно: через радианы.
Для того, чтобы перейти от одной формы записи к другой, используется вот такое основное соотношение:
\( \displaystyle 180<>^\circ =\pi
И все, больше знать ничего не надо!
По пропорции ты легко получишь, что для того, чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:
И наоборот: от радиан к градусам:
Ты должен уметь ориентироваться и в той, и в другой форме записи.
Потренируйся на следующих примерах:
Я сделаю только первые два, а остальные реши сам!
Все очень просто, не так ли? Остальные значения ты можешь найти в следующей таблице:
| \( \displaystyle 0<>^\circ \) | \( \displaystyle 30<>^\circ \) | \( \displaystyle 45<>^\circ \) | \( \displaystyle 60<>^\circ \) | \( \displaystyle 90<>^\circ \) | \( \displaystyle 120<>^\circ \) | \( \displaystyle 135<>^\circ \) | \( \displaystyle 150<>^\circ \) | \( \displaystyle 180<>^\circ \) |
| \( \displaystyle 0\) | \( \displaystyle \frac<\pi ><6>\) | \( \displaystyle \frac<\pi ><4>\) | \( \displaystyle \frac<\pi ><3>\) | \( \displaystyle \frac<\pi ><2>\) | \( \displaystyle \frac<2\pi ><3>\) | \( \displaystyle \frac<3\pi ><4>\) | \( \displaystyle \frac<5\pi ><6>\) | \( \displaystyle \pi \) |
| \( \displaystyle 210<>^\circ \) | \( \displaystyle 225<>^\circ \) | \( \displaystyle 240<>^\circ \) | \( \displaystyle 270<>^\circ \) | \( \displaystyle 300<>^\circ \) | \( \displaystyle 315<>^\circ \) | \( \displaystyle 330<>^\circ \) | \( \displaystyle 360<>^\circ \) |
| \( \displaystyle \frac<7\pi ><6>\) | \( \displaystyle \frac<5\pi ><4>\) | \( \displaystyle \frac<4\pi ><3>\) | \( \displaystyle \frac<3\pi ><2>\) | \( \displaystyle \frac<5\pi ><3>\) | \( \displaystyle \frac<7\pi ><4>\) | \( \displaystyle \frac<11\pi ><6>\) | \( \displaystyle 2\pi \) |
Так что впредь не удивляйся, когда ты увидишь вместо привычных градусов углы в радианах. Теперь ты знаешь, что это такое, и с чем его едят!
Подведем предварительные, но очень важные итоги:
Синус, косинус, тангенс и котангенс на тригонометрической окружности
Но мы с тобой и так слишком увлеклись. Ты давно уже, наверное, заждался обещанных синусов и косинусов на тригонометрической окружности. Не смею более отвлекаться!
Давай сделаем вот что: совместим два знакомых нам объекта: тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.
Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?
Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице.
Совместим мы их вот так:
Я нарисовал прямоугольный треугольник с центром в начале координат и гипотенузой равной \( 1\). Это так потому, что окружность-то у меня единичная!
Тогда по определению синуса и косинуса:
А что же такое отрезки \( OA\) и \( OB\)? Чему равны их длины?
Смотри, сейчас будет самое главное: мы взяли угол \( \alpha \) и провели луч, соединяющий этот угол с точкой на окружности.
Обозначим эту точку через \( B\). Пусть \( B\) имеет координаты \( B\left( x,y \right)\).
Тогда длина отрезка \( OA\) равна \( x\), а длина отрезка \( AB\)–равна \( y\).
Но мы с тобой помним, что \( sin\ \alpha =AB\), \( cos\ \alpha =OA\), тогда:
Ух ты! Это надо еще раз обдумать, что же мы такое получили.
Давай проговорим еще раз: мы выбрали некоторый угол \( \alpha \) и хотим найти его синус и косинус.
Вот и все! Теперь синус и косинус искать стало намного проще! Допустим, мы хотим найти синус, косинус \( 30\) градусов.
Отмечаем \( 30\) градусов на окружности и «достраиваем» этот угол до треугольника (как показано на рисунке выше).
Да очень просто: в прямоугольном треугольнике катет, лежащий против угла в \( 30\) градусов равен половине гипотенузы (это известный факт из геометрии 7 класса).
Так как гипотенуза равна \( 1\), то противолежащий ей катет равен \( 0,5\), откуда:
Что касается косинуса: для этого нам потребуется заметить, что выполняется тривиальное утверждение (основное тригонометрическое тождество):
Как ты думаешь, откуда оно берется? Да это же пресловутая теорема Пифагора!
Наши катеты в треугольничке равны \( x\) и \( y\), которые в свою очередь совпадают с \( cos\ \alpha \) и \( sin\ \alpha \). Гипотенуза в треугольнике равна \( 1\).
Эта формула позволит по известному синусу вычислить неизвестный косинус и наоборот.
Определение знака синуса, косинуса, тангенса и котангенса
Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла \( \displaystyle 30\) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».
Теперь попробуй на основе вышеизложенного найти синус и косинус углов: \( \displaystyle 60<>^\circ \) и \( \displaystyle 45<>^\circ \)
Можно схитрить: в частности для угла в \( \displaystyle 60<>^\circ \) градусов. Так как если один угол прямоугольного треугольника равен \( \displaystyle 60<>^\circ \) градусам, то второй – \( \displaystyle 30<>^\circ \) градусам. Теперь вступают в силу знакомые тебе формулы:
\( \displaystyle sin\ 30<>^\circ =cos\ 60<>^\circ \)
\( \displaystyle sin\ 60<>^\circ =cos\ 30<>^\circ \)
Тогда так как \( \displaystyle sin\ 30<>^\circ =0,5\), то и \( \displaystyle cos\ 60<>^\circ =0,5\). Так как \( \displaystyle cos\ 30<>^\circ =\frac<\sqrt<3>><2>\), то и \( \displaystyle sin\ 60<>^\circ =\frac<\sqrt<3>><2>\).
C \( \displaystyle 45\) градусами все еще проще: так если один из углов прямоугольного треугольника равен \( \displaystyle 45\) градусам, то и другой тоже равен \( \displaystyle 45\) градусам, а значит такой треугольник равнобедренный.
Значит, его катеты равны. А значит равны его синус и косинус.
Откуда: \( \displaystyle sin 45<>^\circ =cos 45<>^\circ =\sqrt<1>=\frac<\sqrt<2>><2>\)
Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в \( \displaystyle 0\) градусов и \( \displaystyle 90\) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!
У тебя должно было получиться:
\( \displaystyle sin\ 0<>^\circ =0\), \( \displaystyle cos\ 0<>^\circ =1\), \( \displaystyle sin\ 90<>^\circ =1\), \( \displaystyle cos\ 90<>^\circ =0\).
Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:
Обрати внимание, что на ноль делить нельзя!!
Теперь все полученные числа можно свести в таблицу:
Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.
Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса \( \displaystyle 90\) градусов. Это неспроста!
Поэтому мы с тобой будем считать, что тангенс \( \displaystyle 90\) градусов и котангенс нуля просто-напросто не определены!
Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:
Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.
Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.
Теперь же пусть наш угол больше \( \displaystyle 90\) градусов и не больше чем \( \displaystyle 360\).
Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.
Как мы поступаем? Да точно так же!
Давай рассмотрим вместо вот такого случая…
…вот такой:
То есть рассмотрим угол \( \displaystyle \alpha \), лежащий во второй четверти. Что мы можем сказать про него?
У точки \( \displaystyle <
Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!
Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.
Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.
Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).
Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.
Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.
Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:
Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.
Задачи на тренировку
Выяснить, какой знак имеют следующие величины:
Задача №2. \( \displaystyle sin\ \frac<2\pi ><3>,\ \cos \ \frac<11\pi ><6>,\ tg\frac<7\pi ><4>\).
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Теперь я хотел бы очень кратко остановиться вот еще на каком моменте. Давай снова вспомним основное тригонометрическое тождество.
Как я уже говорил, из него мы можем выразить синус через косинус или наоборот:
\( \displaystyle sin\ \alpha =\pm \sqrt<1-co<^<2>>\alpha >\)
\( \displaystyle cos\ \alpha =\pm \sqrt<1-si<
На выбор знака же будет влиять только та четверть, в которой находится наш угол альфа. На последние две формулы существует масса задач в ЕГЭ, например, вот таких:
Задача №3
Найдите \( \displaystyle 3cos\alpha \), если \( \displaystyle sin\alpha =-\frac<2\sqrt<2>><3>\) и \( \displaystyle \alpha \in \left( \frac<3\pi ><2>;2\pi \right)\).
На самом деле, это задача на четверть! Смотри, как она решается:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Углы больше 360 градусов
А как быть с углами, большими чем \( \displaystyle 360\) градусов?
Возьму я, скажем, угол в \( \displaystyle 30\) градусов (\( \displaystyle \frac<\pi ><6>\) радиан) и пойду от него против часовой стрелки…
На рисунке я нарисовал спираль, но ты-то понимаешь, что на самом деле у нас нет никакой спирали: у нас есть только окружность.
Так куда же мы попадем, если стартуем от определенного угла и пройдем полностью весь круг (\( \displaystyle 360\) градусов или \( \displaystyle 2\pi \) радиан)?
Куда мы придем? А придем мы в тот же самый угол!
Это же, конечно, справедливо и для любого другого угла:
Взяв произвольный угол \( \displaystyle \alpha \) и пройдя полностью всю окружность, мы вернемся в тот же самый угол \( \displaystyle \alpha \).
Что же нам это даст? А вот что: если \( \displaystyle sin\ \alpha =y,
\( \displaystyle \sin \left( \alpha +2\pi k \right)=y\), \( \displaystyle \cos \left( \alpha +2\pi k \right)=x\), откуда окончательно получим:
\( \displaystyle \sin \left( \alpha +2\pi k \right)=sin\alpha \) \( \displaystyle \cos \left( \alpha +2\pi k \right)=cos\alpha \)
Для любого целого \( \displaystyle k\). Это значит, что синус и косинус являются периодическими функциями с периодом \( \displaystyle 2\pi \).
Таким образом, нет никакой проблемы в том, чтобы найти знак теперь уже произвольного угла: нам достаточно отбросить все «целые круги», которые умещаются в нашем угле и выяснить, в какой четверти лежит оставшийся угол.
Например, найти знак:
Проверяем:
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Промежуточный итог
Итак, ты понял что такое тригонометрическая окружность и для чего она нужна.
Но у нас осталось еще очень много вопросов:
Чтобы узнать ответы на них, читай далее!
Отрицательные углы
Отрицательные углы в тригонометрии откладываются на тригонометрическом круге вниз от начала, по направлению движения часовой стрелки:
Давай вспомним, как мы до этого откладывали углы на тригонометрической окружности.
Мы шли от положительного направления оси \( \displaystyle Ox\) против часовой стрелки:
Тогда на нашем рисунке построен угол, равный \( \displaystyle 180+45=225<>^\circ \). Аналогичным образом мы строили все углы.
Однако ничего нам не запрещает идти от положительного направления оси \( \displaystyle Ox\) по часовой стрелке.
Мы будем тоже получать различные углы, но они будут уже отрицательными:
А следующей картинке изображено два угла, равные по абсолютной величине (если не знаешь, что это такое, читай здесь про «Модуль числа»), но противоположные по знаку:
В целом правило можно сформулировать вот так:
Схематично правило изображено вот на этом рисунке:
Ты мог бы задать мне вполне резонный вопрос: ну углы нам нужны для того, чтобы измерять у них значения синуса, косинуса, тангенса и котангенса.
Так есть ли разница, когда у нас угол положительный, а когда – отрицательный? Я отвечу тебе: как правило есть.
Однако ты всегда можешь свести вычисление тригонометрической функции от отрицательного угла к вычислению функции в угле положительном.
Посмотри на следующую картинку:
Я построил два угла, они равны по абсолютному значению, но имеют противоположный знак. Отметим для каждого из углов его синус и косинус на осях.
Что мы с тобой видим? А вот что:
Тогда если \( \displaystyle \text
Тогда если \( \displaystyle \text
Таким образом, мы всегда можем избавиться от отрицательного знака внутри любой тригонометрической функции: либо просто уничтожив его, как у косинуса, либо поставив его перед функцией, как у синуса, тангенса и котангенса.
Кстати, вспомни-ка, как называется функция \( \displaystyle f(x)\), у которой для любого допустимого \( \displaystyle x\) выполняется:\( \displaystyle f(-x)=-f(x)\)?
Такая функция называется нечетной.
А если же для любого допустимого \( \displaystyle x\) выполняется: \( \displaystyle f(-x)=f(x)\)? То в таком случае функция называется четной.
Таким образом, мы с тобой только что показали, что:
Синус, тангенс и котангенс – нечетные функции, а косинус – четная.
Таким образом, как ты понимаешь, нет никакой разницы, ищем ли мы синус от положительного угла или отрицательного: справиться с минусом очень просто. Так что нам не нужны таблицы отдельно для отрицательных углов.
С другой стороны, согласись, было бы очень удобно зная только тригонометрические функции углов первой четверти, уметь вычислять аналогичные функции и для остальных четвертей.
Можно ли это сделать? Конечно, можно!
У тебя есть по крайней мере 2 пути: первый – строить треугольник и применять теорему Пифагора (так мы с тобой и отыскали значения тригонометрических функций для основных углов первой четверти)
Второй – запомнив значения функций для углов в первой четверти и некое несложное правило, уметь вычислять тригонометрические функции для всех остальных четвертей.
Второй способ избавит тебя от долгой возни с треугольниками и с Пифагором, поэтому мне он видится более перспективным:
Итак, данный способ (или правило) называется формулами приведения.
Формулы приведения
Грубо говоря, эти формулы помогут тебе не запоминать вот такую таблицу (она между прочим содержит 98 чисел!):
…если ты помнишь вот эту (всего на 20 чисел):
То есть ты сможешь не забивать себе голову совершенно ненужными 78 числами! Пусть, например, нам нужно вычислить \( \displaystyle \text
Во-первых, нам понадобятся следующие знания:
Синус и косинус имеют период \( \displaystyle 2\pi \) (\( \displaystyle 360\) градусов)
\( \displaystyle sin\left( 2\pi k+x \right)=sin x\)
\( \displaystyle cos\left( 2\pi k+x \right)=cos x\)
Тангенс (котангенс) имеют период \( \displaystyle \pi \) (\( \displaystyle 180\) градусов)
\( \displaystyle ctg\left( \pi k+x \right)=ctg x\)
\( \displaystyle k\) – любое целое число
Синус и тангенс – функции нечетные, а косинус – четная:
Первое утверждение мы уже доказали с тобой, а справедливость второго установили совсем недавно.
Непосредственно правило приведения выглядит вот так:
Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул о четности.
Отбрасываем для синуса и косинуса его периоды: \( \displaystyle 2\pi k\) (по \( \displaystyle 360\) градусов), а для тангенса – \( \displaystyle \pi k\) (\( \displaystyle 180\) градусов).
\( \displaystyle sin\ 855<>^\circ =sin\left( 2\cdot 360<>^\circ +135<>^\circ \right)=sin\ 135<>^\circ \)\( \displaystyle tg\ 225<>^\circ =tg\left( 180<>^\circ +45<>^\circ \right)=tg\ 45<>^\circ \)
Если оставшийся «уголок» меньше \( \displaystyle 90\) градусов, то задача решена: ищем его в «малой таблице».
Иначе ищем, в какой четверти лежит наш угол \( \displaystyle \alpha \): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак.
Представляем угол \( \displaystyle \alpha \)в одной из следующих форм:
…так, чтобы оставшийся угол \( \displaystyle \beta \) был больше нуля и меньше \( \displaystyle 90\) градусов.
В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Теперь смотрим, что у нас получилось: если ты выбрал запись через \( \displaystyle 180\) или \( \displaystyle 360\) градусов плюс минус что-либо, то знак функции меняться не будет: ты просто убираешь \( \displaystyle 180\) или \( \displaystyle 360\) и записываешь синус, косинус или тангенс оставшегося угла.
Если же ты выбрал запись через \( \displaystyle 90\) или \( \displaystyle 270\) градусов, то синус меняем на косинус, косинус на синус, тангенс на котангенс, котангенс – на тангенс.
Ставим перед получившимся выражением знак, который мы запомнили.
Давай продемонстрируем все вышесказанное на примерах: