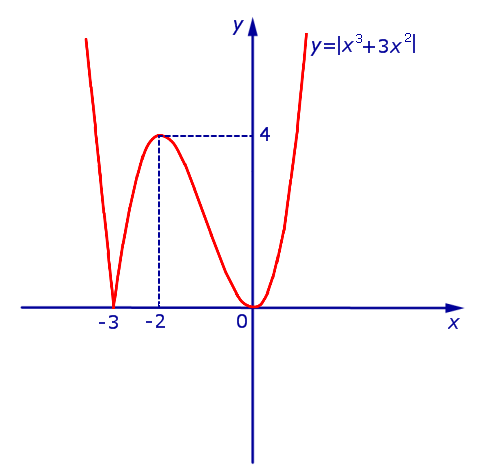
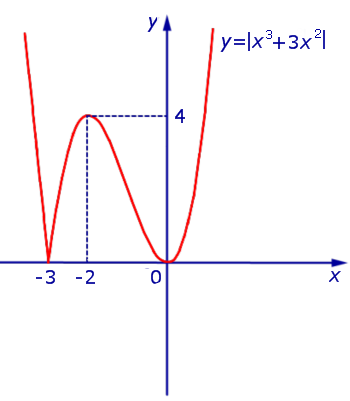
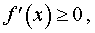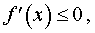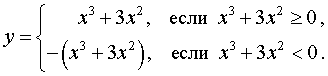как определить на каком промежутке функция возрастает а на каком убывает

Возрастание и убывание функции на интервале, экстремумы

Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.

Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.

Возрастание и убывание функции на интервале

Точки экстремума, экстремумы функции

Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Достаточные условия возрастания и убывания функции

Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.

Первое достаточное условие экстремума

Иначе говоря, получим их условия постановки знака:

Алгоритм для нахождения точек экстремума

Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:

Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.

Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.

Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид

Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:

После чего необходимо найти производную:

Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:

Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:

Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что

Перейдем к вычислению минимумов:

Произведем вычисления максимумов функции. Получим, что

Второй признак экстремума функции

Для начала находим область определения. Получаем, что

Необходимо продифференцировать функцию, после чего получим

Третье достаточное условие экстремума

Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что

Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.

Источник

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №15. Возрастание и убывание функции.

Перечень вопросов, рассматриваемых в теме

1) Нахождение промежутков монотонности функции,

2) Определение алгоритма нахождения промежутков возрастания и убывания функции,

3) Решение задачи на нахождения промежутков возрастания и убывания функции

Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х₁ и х₂ из этого промежутка из неравенства х₁ f(x₂)

Примеры и разбор решения заданий тренировочного модуля

№1. Определите промежутки монотонности функции

1.Найдем область определения функции.

D(y) =

2.Найдем производную функции.

3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).

Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

Так как на интервале производная функции отрицательна, то на этом интервале функция убывает.

Так как на интервале производная функции положительна, то на этом интервале функция возрастает.

Так как на интервале производная функции отрицательна, то на этом интервале функция убывает.

Так как в точках функция непрерывна, то эти точки входят в промежутки возрастания и убывания данной функции.

Следовательно, функция возрастает на ; функция убывает на и на .

Ответ: Функция возрастает на

Функция убывает на и на .

№2. Определите промежутки монотонности функции

у = х 5 –5х 4 +5х 3 – 4.

y‘ =

Ответ: Функция возрастает на ;

функция убывает на .

Источник

Исследование поведения функций с помощью производной

Интервалы возрастания и убывания функции

Достаточные условия для возрастания и убывания функции

Экстремумы (максимумы и минимумы) функции

«Подозрительные» на наличие экстремума точки функции. Теорема Ферма

Достаточные условия для существования экстремума функции

Пример исследования поведения функции

Интервалы возрастания и убывания функции

Для того, чтобы найти интервалы, на которых функция возрастает или убывает, часто используется метод, основанный на анализе знаков производной рассматриваемой функции. Суть этого метода состоит в следующем.

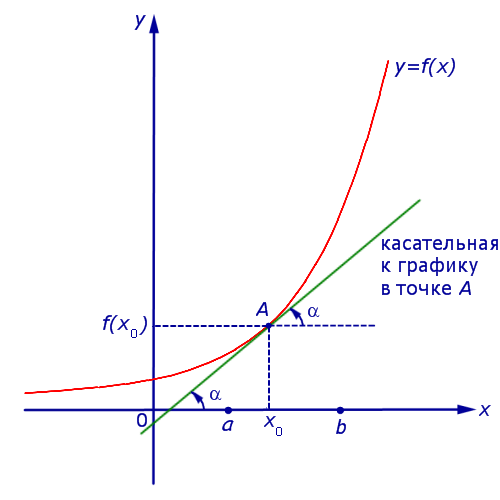
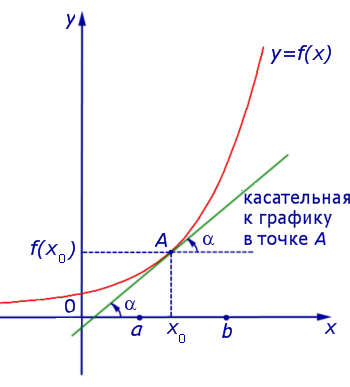
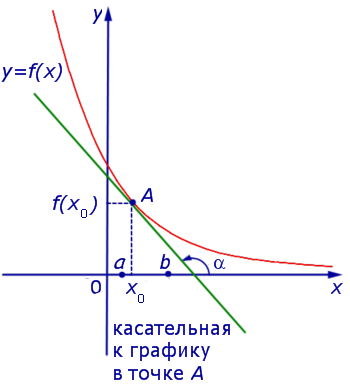
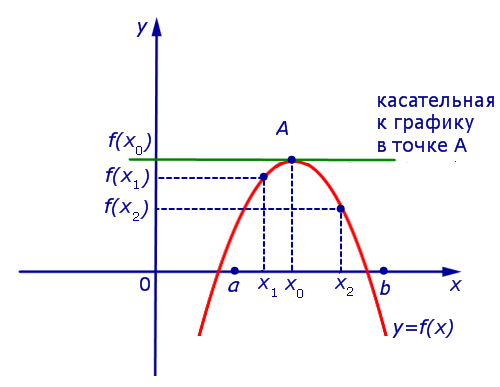
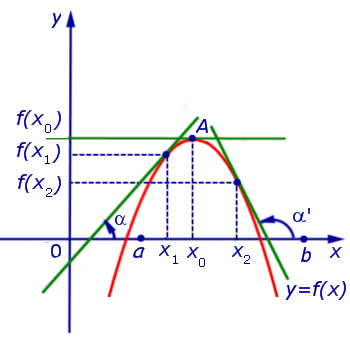
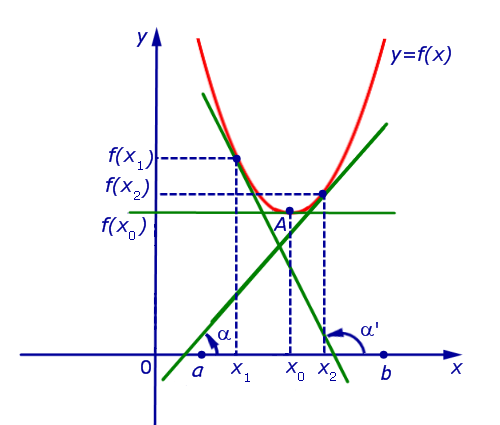
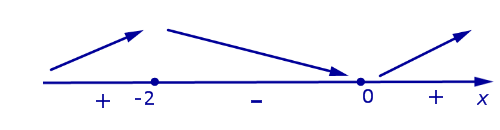
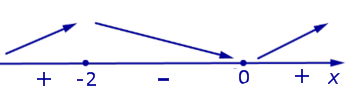
Если на интервале (a, b) функция y = f (x) строго возрастает и в каждой точке x₀ интервала имеет производную, то, как показано на рисунке 1, а также на рисунке 2,

угол α наклона касательной к графику функции будет острым, откуда вытекает неравенство:

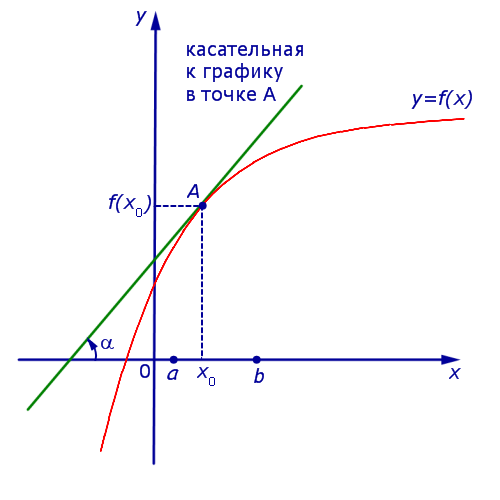
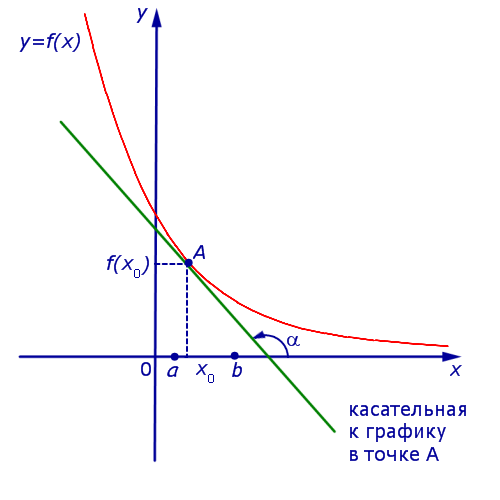
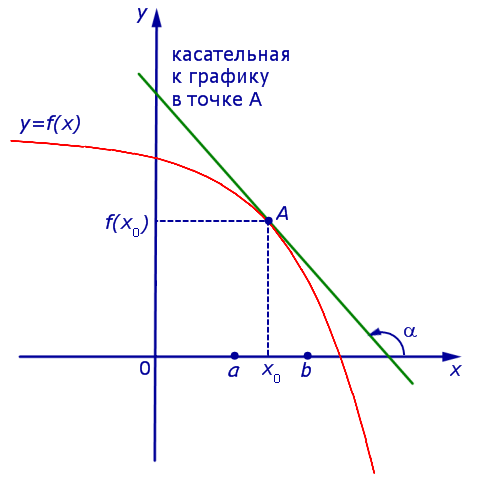
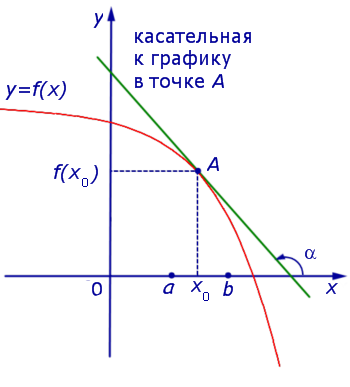
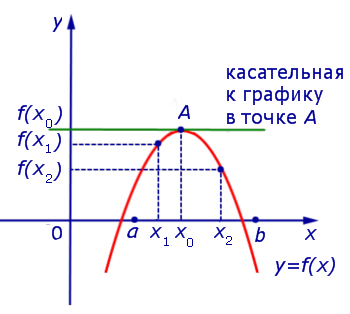
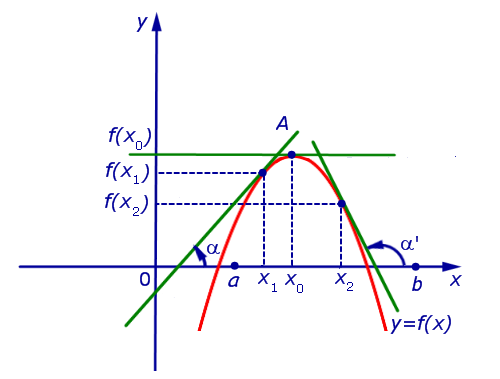
Если же на интервале (a, b) функция y = f (x) строго убывает и в каждой точке x₀ интервала имеет производную, то, как показано на рисунках 3 и 4,

угол α наклона касательной к графику функции будет тупым, откуда вытекает неравенство:

а). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству

б). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству

в). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству

г). Если в каждой точке x интервала (a, b) производная f ‘ (x) существует и удовлетворяет неравенству

Экстремумы (максимумы и минимумы) функции

.

.

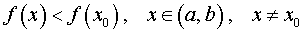
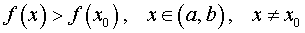
«Подозрительные» на наличие экстремума точки функции.
Теорема Ферма

Определение 4. Стационарной точкой функции называют такую точку, в которой производная функции равна нулю.

Определение 5. Критической точкой функции называют такую точку, в которой производная функции равна нулю или не существует.

Таким образом, если точка x₀ является критической точкой функции, то точка x₀ либо является стационарной точкой функции, либо производная функции в точке x₀ не существует.

.

.

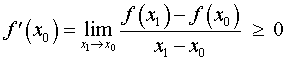
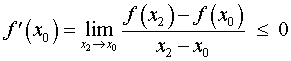
Достаточные условия для существования экстремума функции

В следующем утверждении, доказательство которого выходит за рамки школьного курса математики и в нашем справочнике не приводится, сформулированы достаточные условия для экстремума функции.

а). Если для точек 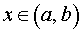выполнено условие:

б). Если для точек 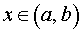выполнено условие:

Пример исследования поведения функции

Пример. Найти интервалы возрастания, убывания и экстремумы функции

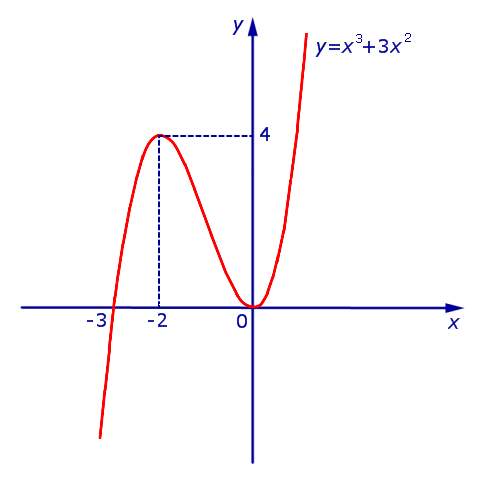
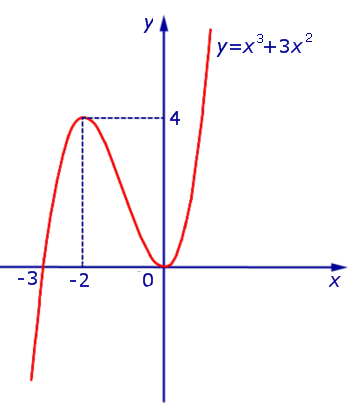
Решение. Исследуем сначала на возрастание, убывание и экстремумы функцию

и построим ее график. Для этого представим формулу (2) в виде

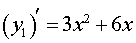(3)

и разложим на множители правую часть формулы (3):

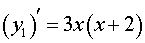(4)

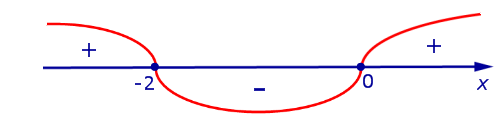
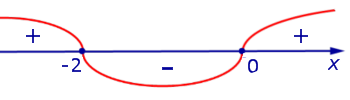
На рисунке 8 при помощи метода интервалов изобразим на числовой оси знаки производной (4)

Поскольку решением неравенства

,

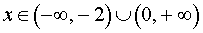(5)

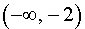
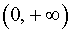
то в соответствии с утверждением 1 функция y₁ возрастает на каждом из интервалов и .

С другой стороны, поскольку решением неравенства

Так как решениями уравнения

Заметим, что при анализе поведения функции по знакам ее производной, удобно использовать следующую диаграмму, на которой стрелками указаны интервалы возрастания и убывания функции (рис. 9).

В силу определения модуля, справедливо равенство

В точке x = – 3 производная функции y = | x 3 + 3x 2 | не существует. Во всех остальных точках числовой оси производная функции y = | x 3 + 3x 2 | существует.

Функция y = | x 3 + 3x 2 | возрастает на каждом из интервалов (– 3, – 2) и .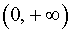

Источник

Возрастание и убывание функции

Общие понятия о поведении функций

Исследуя функции, заданные определенными уравнениями, особенно уделяют внимание их свойствам, а именно возрастанию или убыванию.

Монотонной функцией называется функция, меняющаяся в одном направлении.
На графиках представлены примеры монотонно возрастающей и монотонно убывающей функций.

Соответственно, монотонная функция может быть возрастающая или убывающая.

Возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается, иными словами, чем больше значение аргумента, тем больше значение функции.

Математическое выражение этого определения выглядит следующим образом:

Убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается, иными словами, чем больше значение аргумента, тем меньшее значение функции.

Математическое выражение этого определения выглядит следующим образом:

Разберем примеры решения задач на изучение характера поведения функции.

Поскольку значения функции увеличиваются, при увеличении значений аргумента, то данная функция на заданном отрезке будет возрастать.

Поскольку значения функции уменьшаются, при увеличении значений аргумента, то данная функция на данном отрезке будет убывать.

Не возрастающей называется такая функция, у которой при увеличении значения аргумента, значение функции увеличивается или остается на том же уровне, иными словами, большему значению аргумента соответствует большее или равное значение функции.

Не нашли что искали?

Просто напиши и мы поможем

Не убывающей называется такая функция, у которой при увеличении значения аргумента, значение функции уменьшается или остается на том же уровне, иными словами, большему значению аргумента соответствует меньшее или равное значение функции.

Постоянной называется такая функция, которая не убывает и не возрастает, то есть при увеличении или при уменьшении значения аргумента, значение функции остается на одном и том же уровне. Пример такой функции можно наблюдать на рисунке.

То есть функция \(y=5\) будет постоянной.

Постоянная, не убывающая и не возрастающая функции не есть монотонные.

Свойства монотонных функций

К свойствам монотонных функций относятся такие характеристики:

Монотонность производной и заданной функций связаны между собой, и это описано в таких теоремах:

Источник

«Возрастание и убывание функции»

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Возрастание и убывание функций

а b Признак возрастания функции y=f(x) M3 M1 M2

а b Признак убывания функции y=f(x) M3 M1 M2

Как определить промежутки убывания и возрастания функции Пример 1 Пример 2 Алгоритм: Найти производную функции f'(x). 2. Найти стационарные (f'(x)=0) и критические (f'(x) не существует) точки функции у= f(x). 3. Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках. 4. Сделать выводы о промежутках возрастания и убывания функции.

Как определить промежутки убывания и возрастания функции Посмотреть график функции Х Алгоритм

График функции Х График функции

График функции Х График функции

. а) у = х³ — 6 х² + 9 х — 9; б) у = 3 х² — 5х + 4.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

«Возрастание и убывание функции»

1. Научить находить промежутки монотонности.

2. Развитие мыслительных способностей, обеспечивающих анализ ситуации и разработку адекватных способов действия (анализ, синтез, сравнение).

3. Формирование интереса к предмету.

Сегодня мы продолжаем изучать приложение производной и рассмотрим вопрос о её применениик исследованию функций. Фронтальная работа

А теперь дадим некоторые определения свойствам функции “Мозговой штурм”

1. Что называют функцией?

2. Как называется переменная Х?

3. Как называется переменная Y?

4. Что называется областью определения функции?

5. Что называется множеством значения функции?

6. Какая функция называется чётной?

7. Какая функция называется нечётной?

8. Что можно сказать о графике чётной функции?

9. Что можно сказать о графике нечётной функции?

10. Какая функция называется возрастающей?

11. Какая функция называется убывающей?

12. Какая функция называется периодической?

Математика изучает математические модели. Одной из главнейших математических моделей является функция. Существуют разные способы описания функций. Какой самый наглядный?

– Как построить график?

Этот способ подойдет, если заранее известно, как примерно выглядит график. Например, что является графиком квадратичной функции, линейной функции, обратной пропорциональности, функции y = sinx? (Демонстрируются соответствующие формулы, учащиеся называют кривые, являющиеся графиками.)

А что если требуется построить график функции или еще более сложной? Можно найти несколько точек, но как ведет себя функция между этими точками?

Поставить на доске две точки, попросить учеников показать, как может выглядеть график “между ними”:

Выяснить, как ведет себя функция, помогает ее производная.

Откройте тетради, запишите число, классная работа.

Цель урока: узнать, как связан график функции с графиком ее производной, и научиться решать задачи двух видов:

1. По графику производной находить промежутки возрастания и убывания самой функции, а также точки экстремума функции;

2. По схеме знаков производной на промежутках находить интервалы возрастания и убывания самой функции, а также точки экстремума функции.

Подобные задания отсутствуют в наших учебниках, но встречаются в тестах единого государственного экзамена (часть А и В).

Для решения поставленной задачи, нам необходимо вспомнить некоторые вопросы, рассмотренные ранее.

Итак, запишем тему сегодняшнего урока: Признаки возрастания и убывания функции.

Признаки возрастания и убывания функции:

Если производная данной функции положительна для всех значений х в интервале (а; в), т.е.f'(x) > 0, то функция в этом интервале возрастает.
Если производная данной функции отрицательна для всех значений х в интервале(а; в), т.е.f'(x)

Порядок нахождения промежутков монотонности:

Найти область определения функции.

1. Найти первую производную функции.

2. решать самой на доске

Найти критические точки, исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции. Найти промежутки монотонности функций:

б) найдем первую производную:,

3. Исследуем знак производной в полученных промежутках, решение представим в виде таблицы.

указать на точки экстремума

Рассмотрим несколько примеровисследования функции на возрастание и убывание.

Достаточное условие существования максимума состоит в смене знака производной при переходе через критическую точку с «+» на «-«, а для минимума с «-» на «+». Если при переходе через критическую точку смены знака производной не происходит, то в данной точке экстремума нет

3. Найти стационарные точки, т.е. точки, где f'(x) = 0 или f'(x) не существует.
(Производная равна 0 в нулях числителя, производная не существует в нулях знаменателя)

4. Расположить Д(f) и эти точки на координатной прямой.

5. Определить знаки производной на каждом из интервалов

6. Применить признаки.

. Закрепление нового материала.

Учащиеся работают в парах, решение записывают в тетрадях.

а) у = х³ — 6 х² + 9 х — 9;

Двое работают у доски.

а) у = 2 х³ – 3 х² – 36 х + 40

Домашнее задание: тест (дифференцированный)

Источник