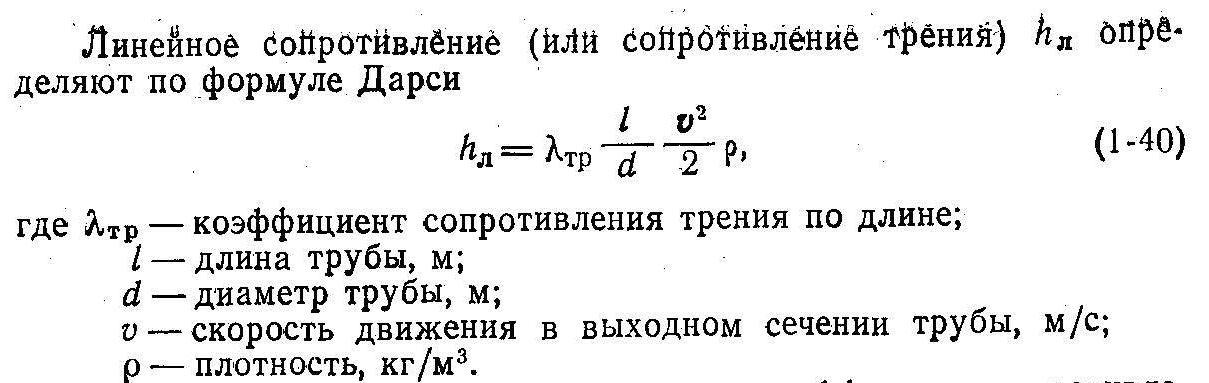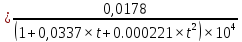как лабораторным путем определить потери на каком либо участке трубы

Что такое потери напора?

Третья статья в цикле статей по теоретическим основам гидравлики посвящена определению потерь напора.

Как рассказывалось ранее, при своем движении жидкость испытывает сопротивление, что выражается затратами ее энергии, т.е. затратами ее напора, что называют потерями напора.

Два вида потерь напора

Потери напора принципиально делятся на два типа:

Местные потери конкретно на данном рисунке: поворот, задвижка (условное обозначение по ГОСТ – «бантик»), еще один поворот и внезапное (т.е. не плавное) расширение.

Местные потери

Местные потери напора (говорят также “потери напора на местные сопротивления“) – это потери напора, которые происходят в основном из-за вихреобразования в конкретных местах трубопровода (потому и «местные»). Любое препятствие на пути движения потока жидкости является местным сопротивление. Чем сильнее деформируется поток, тем больше будет потеря напора. Например, на рисунке ниже показано внезапное сужение трубопровода. Хорошо видны 4 вихревые зоны до и после сужения.

Местную потерю напора можно определить, зная коэффициент сопротивления для данного сопротивления (обозначается буквой дзэта ζ, не имеет размерности) и среднюю скорость потока в сопротивлении V.

Пример. Определить потерю напора в вентиле, установленном на трубе внутренним диаметром d = 51 мм, при расходе Q = 2 л/с.

Сначала по уравнению неразрывности (ссылка на статью 2) определим среднюю скорость движения жидкости.

V = Q / ω = 4 · Q / 3,14 · d² = 4 · 0,002 / 3,14 · 0,051² = 0,98 м/с

Теперь необходим коэффициент сопротивления вентиля. Такие данные берут из гидравлических справочников или у производителей конкретной арматуры. По справочным данным находим, что коэффициент местного сопротивления вентиля равен 6.

Тогда потеря напора на вентиле: h_вент = ζ · V²/ 2 · g = 6 · 0,98² / 2 · 10 = 0,29 м.

Иллюстрация местных потерь напора

При расчете трубопроводных систем (внутренний водопровод здания, наружная водопроводная сеть и т.п.) обычно высчитывают не все сопротивления (так как их может быть очень много), а только самые существенные, создающие наибольшие сопротивления: например, счетчик воды. Потеря напора на остальных местных сопротивлениях учитывается коэффициентом, на который умножается значение потерь напора по длине (1,05 – 1,15 для наружных сетей, 1,1 – 1,3 для внутренних сетей здания).

Потери по длине

Потери напора по длине – потери напора на участках трубопровода. Возникают из-за работы сил трения. (сила трения возникает между слоями движущейся жидкости). Величина потерь напора, также, как и местных потерь, напрямую зависит от скорости движения жидкости. При достаточно высокой скорости усиливается влияние шероховатости стенок трубы.

Потерю напора по длине можно увидеть по разнице в уровнях воды между двумя пьезометрами

Точное определение потерь напора по длине является довольно сложной задачей, для этого необходимо устанавливать режим движения жидкости (бывает ламинарный и турбулентный), подбирать расчетную формулу для коэффициента гидравлического трения в зависимости от числа Рейнольдса Re, характеризующего степень турбулизации потока. Это изучается студентами в рамках курса механики жидкости.

При этом для быстрого расчета потерь напора были составлены специальные таблицы для инженеров, позволяющие, зная материал трубы и ее диаметр, а также расход воды, быстро определить так называемые удельные потери напора (сколько напора теряется на 1 м трубы). Эта величина называется 1000i, значение 1000i = 254 означает, что поток, проходя 1 м такой трубы теряет 254 мм (миллиметра) напора, т.е. 0,254 метра. Это значение также называется «гидравлический уклон», и это нельзя путать с геодезическим, т.е. просто с физическим уклоном (наклоном) самой трубы. Для расчета стальных труб используют таблицы Шевелева.

Скачать таблицы таблицы Шевелева в формате PDF можно на нашем сайте.

Таблицы Шевелева для определения потерь напора

Например, из данного фрагмента видно, что если вода с расходом 1,50 л/с пойдет по трубе диаметром 50 мм, то скорость в этой трубе будет 0,47 м/с, а 1000i составит 9,69 мм на метр (на каждом метре трубы теряется 9,69 миллиметров напора).

Чтобы определить, сколько метров напора будет потеряно на всем участке – нужно перемножить 1000i с длиной участка. Чтобы ответ получился в метрах, 1000i делят на 1000.

Итак, потери напора по длине: h_l = 1000i·l / 1000 = i·l

Если наш участок трубы имеет длину, скажем, 25 метров, то потеря напора на нем:

h_l = 9,69*25/1000 = 0,24 м.

Учтем и местные сопротивления, тогда полная потеря напора на данном участке:

Таблицы были переведены в электронный вид в виде программы, созданной Любчуком Ю.Е.
Загрузить программу “Таблицы Шевелева” можно с нашего сайта.

С помощью этой программы, можно легко посчитать потери напора в трубах из различных материалов. В следующей статье подробно опишем, как пользоваться данной программой на задаче из жизни.

Источник

Лабораторно-практическая работа №3 «Расчет потерь напора в трубопроводах»

Инструкционная карта к практической работе №3 по дисциплине Гидравлика содержит теоретические сведения, необходимые для успешного выполнения работы, а так же три задачи на определение потерь напора в трубопроводе, исходные данные разбиты на три варианта.

Просмотр содержимого документа
«Лабораторно-практическая работа №3 «Расчет потерь напора в трубопроводах»»

ИНСТРУКЦИОННАЯ КАРТА №3

ПО ДИСЦИПЛИНЕ «ОСНОВЫ ГИДРАВЛИКИ, ПНЕВМАТИКИ И ТЕПЛОТЕХНИКИ»

Тема: Уравнение Бернулли для идеальной и реальной жидкости

Практическая работа №3

Тема «Расчет потерь напора в трубопроводах»

Цель: Приобретение практических навыков решения задач на определение числа Рейнольдса, расчета потери напора в трубопроводах по длине.

В.Г. Ерохин, М.Г. Маханько «Сборник задач по основам гидравлики и теплотехники», М.: «Энергия», 1979, стр. 18-26.

Оборудование и принадлежности: инструкционная карта, калькулятор, справочные таблицы.

Задание: Используя изученные формулы, решите следующие задачи:

Определить потерю напора в прямом трубопроводе длиной l =1000 м, по которому прокачивается нефтепродукт с плотностью ρ= 900 кг/м 3 в количестве V = 31,4 л/с. Внутренний диаметр трубопровода dв = 200 мм, коэффициент гидравлического сопротивления λ =0,04(Ерохин 1-58, стр. 33).

Задачу решите по формуле Дарси, предварительно вычислив площадь сечения трубы по внутреннему диаметру и скорость движения в выходном сечении по объемному расходу. Ответ оформите в виде таблицы, оставив только свой вариант.

По трубопроводу с внутренним диаметром dв= 150 мм протекает пар с давлением p_абс=100 кгс/см 2 и температурой t=370 0 С. Скорость пара v=40 м/с. Определить часовой расход пара и критерий Рейнольдса (Ерохин 1-57, стр. 33).

Часовой расход пара определяется как произведение площади поперечного сечения трубопровода на среднюю скорость потока, площадь сечения трубы определяется по внутреннему диаметру. Критерий Рейнольдса определите по значению кинематической вязкости.

Коэффициент кинематической вязкости можно определить по заданной температуре пара:

Ответ оформите в виде таблицы, оставив только свой вариант

Источник

Как лабораторным путем определить потери на каком либо участке трубы

Расход воды в системе водоснабжения связан с сечением трубы и скоростью движения следующей зависимостью:

Рисунок 426. (11)

Рисунок 427. (12)

Практически не представляется возможным установить какие-либо обоснованные пределы колебания расчетной скорости движения воды в трубах, исходя из чисто технических соображений [1]. Между тем, легко видеть, что изменение скорости (при заданном расчетном расходе) существенно влияет на экономические показатели системы водоснабжения. Из приведенной выше формулы видно, что с увеличением скорости диаметр водопровода уменьшается, что обуславливает снижение его строительной стоимости. В свою очередь увеличение скорости влечет за собой увеличение потерь напора в водопроводной сети. Потери напора при движении воды по трубам пропорциональны их длине и зависят от диаметра труб, расхода воды (скорости течения), характера и степени шероховатости стенок труб (то есть от материала труб) и от области гидравлического режима их работы. Основной формулой инженерной гидравлики, связывающей все указанные характеристики, является формула Дарси-Вейсбаха:

Рисунок 428. (13)

где — линейные потери напора, м;

— коэффициент гидравлического сопротивления;

Режим движения жидкости определяется числом Рейнольдса

Рисунок 429. (14)

— кинематический коэффициент вязкости воды при температуре воды 10 ºС.

Смена режимов движения происходит при критических числах Рейнольдса .

Критерием режима движения служат следующие неравенства:

Рисунок 430. (15)

При , коэффициент гидравлического сопротивления можно определить по формуле Колбрука-Уайта

Рисунок 431. (16)

Где коэффициент эквивалентной шероховатости, м.

Область перемежающейся турбулентности

Рисунок 432. (17)

Коэффициент гидравлического сопротивления можно определить по формуле

Рисунок 433. (18)

При смене режимов движения жидкости и сопротивление трубопроводов практически незначительно отклоняется от закономерностей, соответствующих ламинарному режиму движения.

Возможные расхождения при расчете коэффициента гидравлического сопротивления по различным формулам, предложенным авторами Ф.А.Шевелевым А.Д. Альтшулем, Г.А. Муриным, Б.Л.

Шифринсоном, Колбруком-Уайтом при незначительны по сравнению с теми ошибками, которые обычно имеют место вследствие неопределенности в выборе значения шероховатости или степени зарастания трубопровода.

При расчете коэффициента гидравлического сопротивления в случае, когда наиболее целесообразно на наш взгляд использовать зависимость Колбрука-Уайта.

Источник

Лабораторная работа № 5 определение потери напора в прямой трубе

1. Сущность и цель работы

Потеря напора по длине трубы определяется по формуле Дарси – Вейсбаха

, (1)

V – средняя скорость;

l – коэффициент гидравлического сопротивления трения (коэффициент Дарси).

(2)

где D – абсолютная шероховатость, n – кинематический коэффициент вязкости жидкости.

При расчетах сначала определяют область гидравлического сопротивления, затем выбирают расчетную формулу.

Вид функции (2) впервые был установлен опытами Никурадзе, выполненными для плотной, однородной, равномерной шероховатости из песка, нанесенной на внутреннюю поверхность круглых труб.

Были определены следующие области сопротивления:

1) область ламинарного течения Re 500

Расчетная формула Никурадзе

, (8)

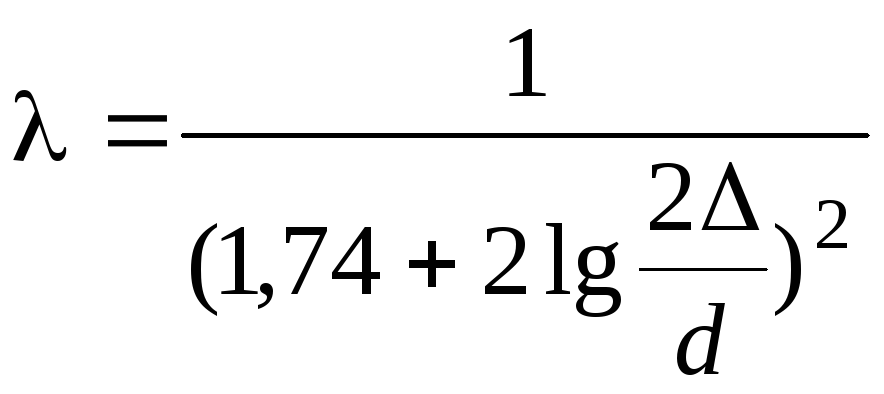
или формула Шифринсона

. (9)

Коэффициент сопротивления lв этой области обычно имеет значенияl= 0,02…0,05.

Целью настоящей работы является:

1. Определение потери напора h_l при движении воды расчетным путем по формуле Дарси – Вейсбаха и опытным путем по показаниям пьезометров.

2. Сравнение полученных результатов и определение погрешности опыта.

2. Описание установки

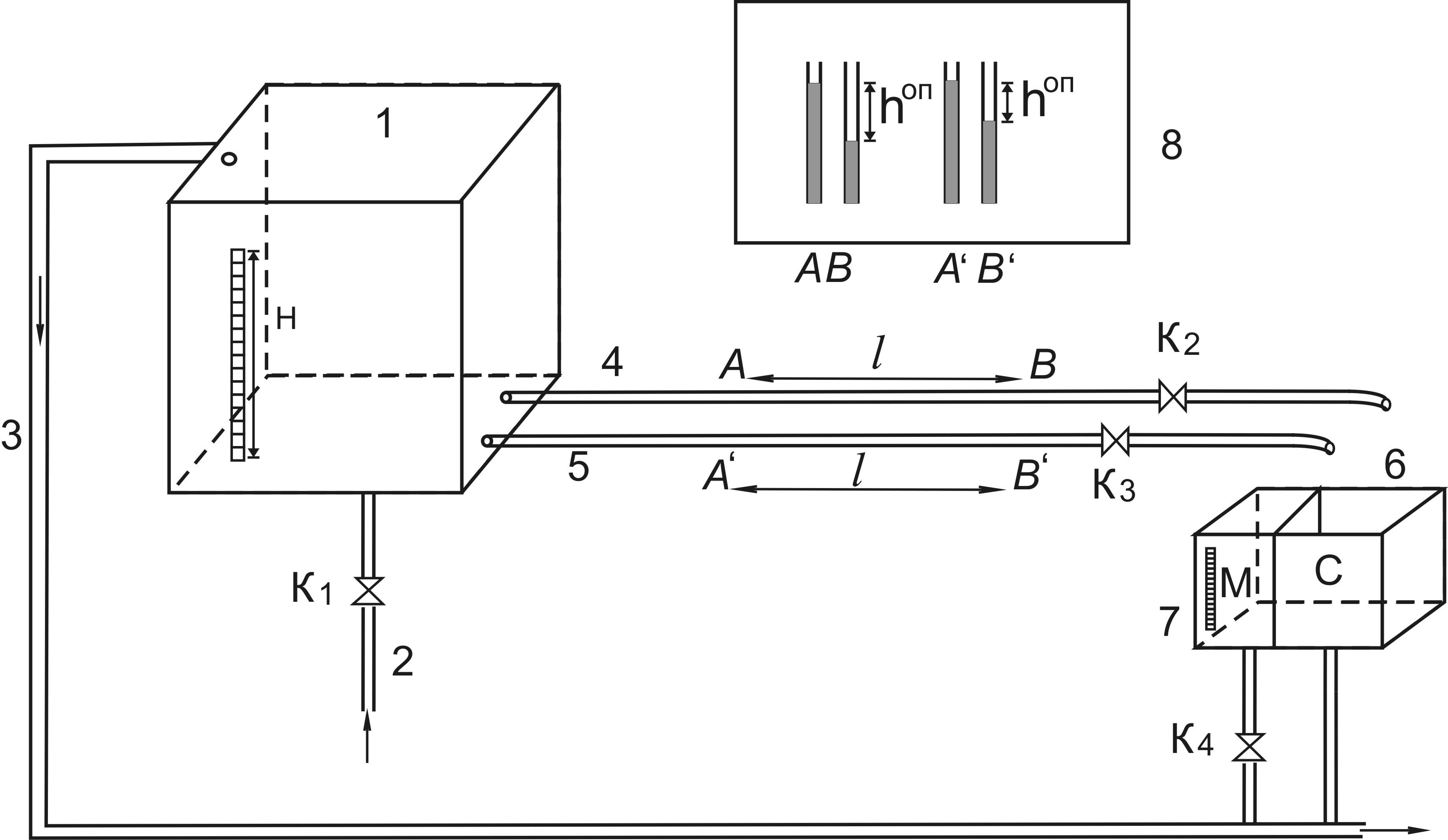
Напорный бак 1 (рис. 8) присоединен к водопроводной сети 2 с помощью крана К₁. Труба 3 соединяет напорный бак с канализацией, предохраняя его от переполнения. Две горизонтально расположенные трубы 4 и 5 одинакового диаметра (d₁=d₂=20 мм) сделаны из разных материалов имеющих разную величину эквивалентной шероховатости (Δ=0,02 мм и Δ=0,2 мм). На конце каждой из этих труб установлены регулировочные краны К₂ и К₃, позволяющие изменять расход воды. Бак 6 имеет перегородку, которая делит его на два отсека С и М (сливной и мерный).

В зависимости от положения гибкого шланга, надетого на трубу, поток из трубы направляется либо в сливной С, либо в мерный М отсек бака. Количество воды в мерном отсеке определяется с помощью водомерного стекла 7. На стенде над трубами расположена панель измерительных инструментов 8, на которой расположены пьезометры, измеряющие потери напора h_l на соответствующих рабочих участках трубы l_АВ на трубе 4 и l_A’B’ на трубе 5.

3. Порядок выполнения работы.

Испытания проводить отдельно для трубы 4, затем для трубы 5.

Установить постоянный напор в баке 1 (), регулируя расход в трубе кранами(или) и краномна входе в напорный бак.

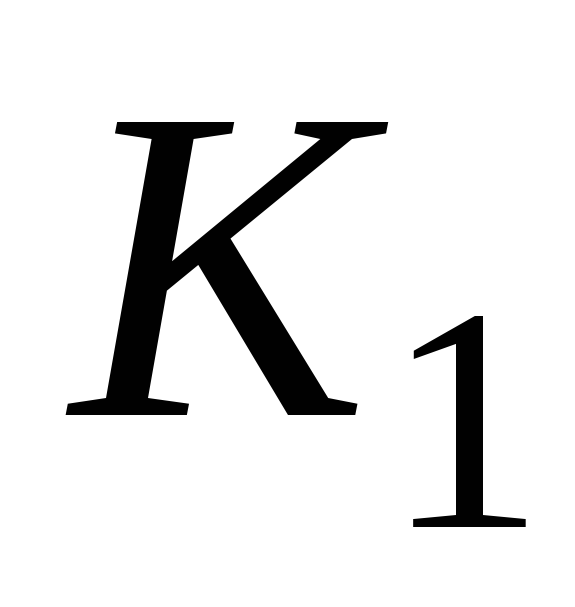
Определить потери напора по разности показаний пьезометров: 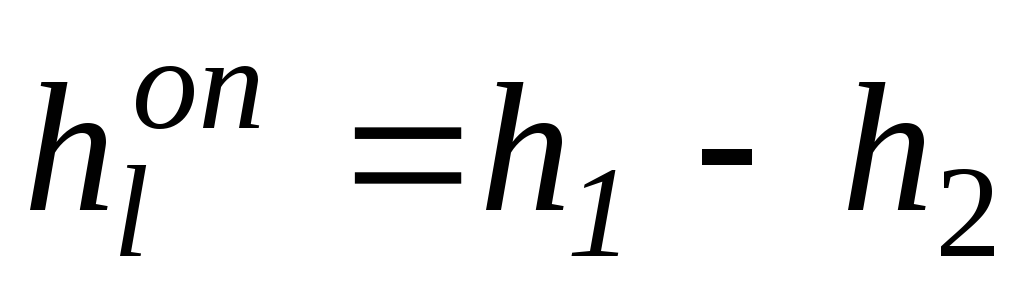, на участке путим.

Определить расход воды Q, замеряя его объемным методом,

,

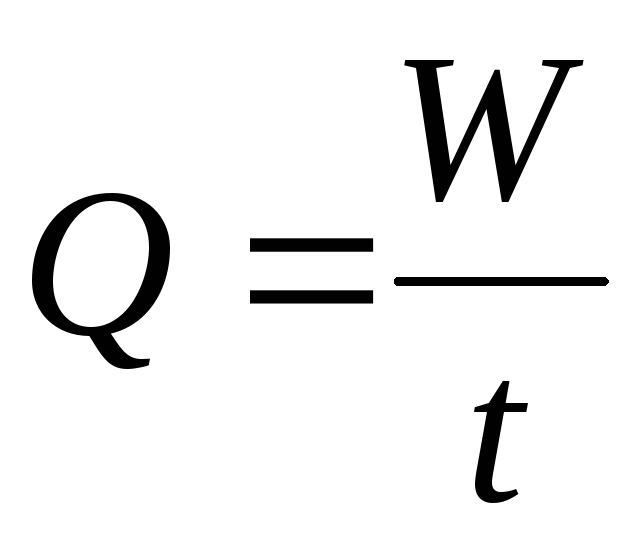
где t – время заполнения объема W мерного бака 6.

Определить среднюю скорость живого сечения

,

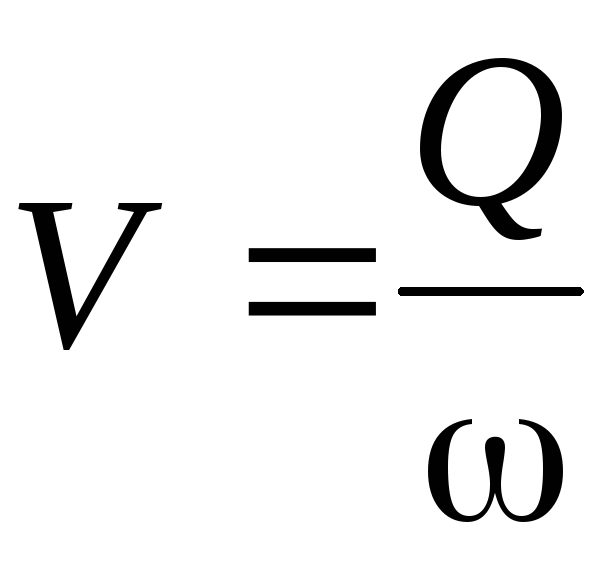
где 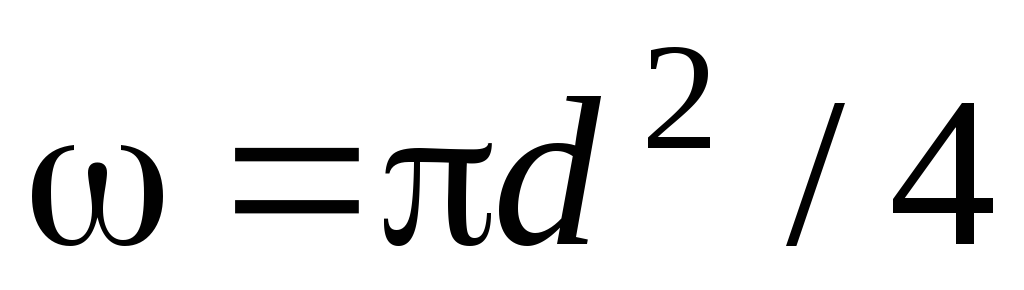– площадь живого сечения.

По измеренной температуре T в мерном баке 6 определить коэффициент кинематической вязкости (см. табл. 7) и вычислить число Рейнольдса:

.

Источник

Как лабораторным путем определить потери на каком либо участке трубы

Лабораторная работа: Изучение потерь напора по длине при равномерном движении жидкости

напора по длине при установившемся движении воды в круглоцилиндрической трубе и практического использования основного уравнения гидродинамики – уравнения Даниила Бернулли.

Рис. 1. Схема опытной установки для определения потерь напора по длине

2.2 Исходные данные

— материал трубы – сталь;

— внутренний диаметр опытного трубопровода d = 21 мм;

— площадь поперечного сечения опытного трубопровода S =0.000346, м 2 ;

Определение потерь напора на расчетных участках

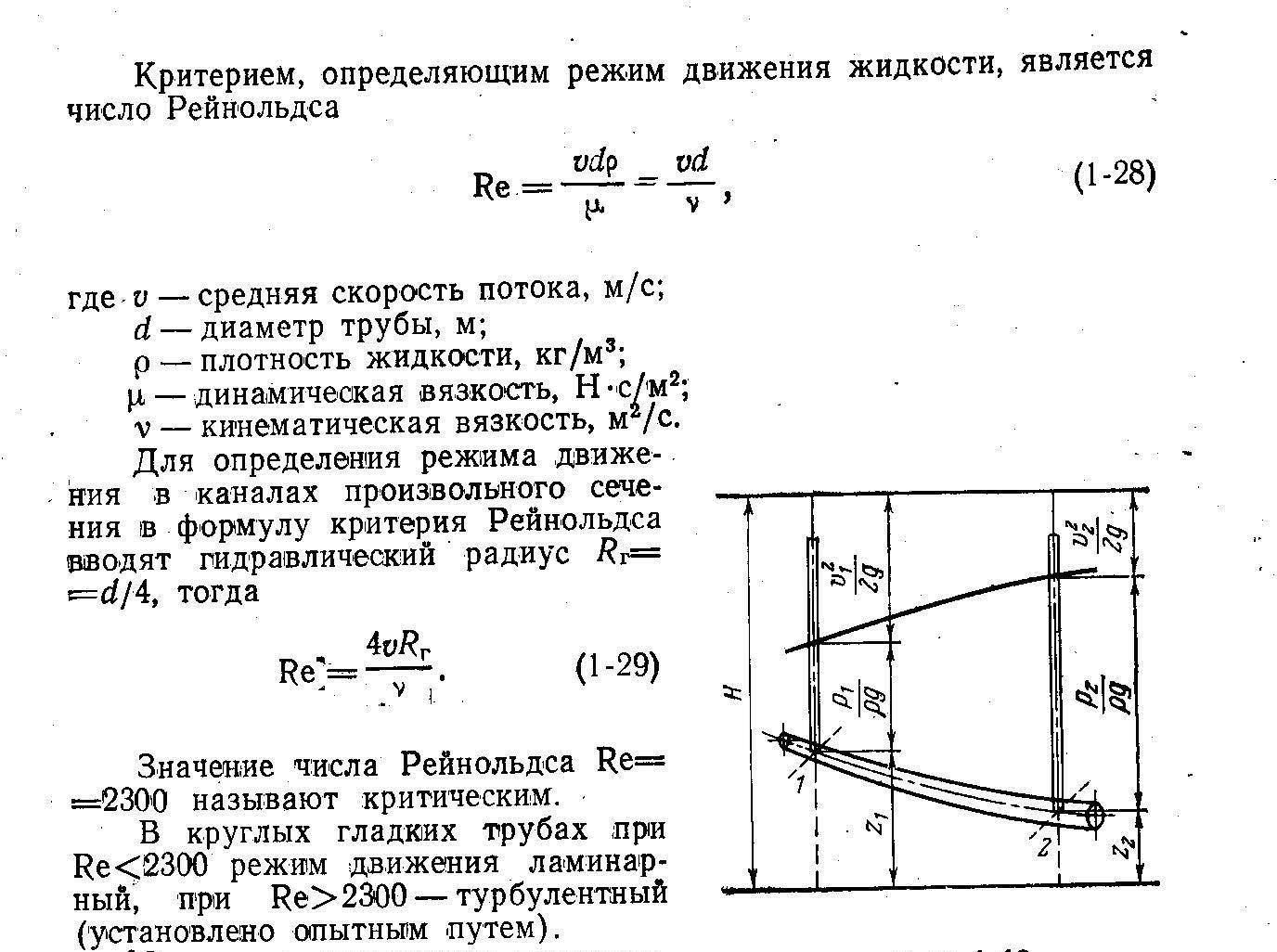
Запас полной механической энергии движущегося объема жидкости, отнесенной к его тяжести, называют полный напором Н. Единицы измерения напора: Дж/H = H м/м = м.

В соответствии с законом сохранения энергий, для двух сечений 1-1 и 2-2 стационарного потока идеальной жидкости, движущейся равномерно, имеем:

В действительности же при движении реальной жидкости в трубопроводах имеют место потери ее механической энергии. Эти потери энергии связаны с наличием сил трения по длине потока, а также с изменением сечения и направления движения потока жидкости в мест­ных сопротивлениях (коленах, тройниках, задвижках, вентилях и т.д.). В этом случае имеем:

где h_пот (1-2) – потеря напора между сечениями 1-1 и 2-2 потока жидкости.

где h_l – потеря напора на трение по длине потока или линейная потеря напора,м;

h_m– местная потеря напора, м.

Линейные потери напора в круглых трубах при равномерном движении жидкости определяют по формуле Дарси-Вейсбаха:

где – коэффициент гидравлического трения или гидравлического сопротивления;

l,d – соответственно, длина и внутреннийдиаметр трубопровода расчетного участка, м;

V – средняя скорость движения води в трубопроводе расчетного участка, м/с;

Местные потери напора находят по формуле Вейсбаха:

Значение величины в формуле (2.7) определяется по выражениям [3, 6]:

— неновые стальные и чугунные трубы:

где k_l – коэффициент, учитывающий потери напора в местных сопротивлениях трубопровода; при расчетах хозяйственно-питьевого водопровода жилых и общественных зданий принимается

h_l – потеря напора на трение по длине трубопровода,м.

Формулу (2.7) в инженерной практике, как правило, применяют в преобразованной форме в виде следующих выражений:

где A_l – удельное сопротивление трубопровода, c 2 /м 6 ;

q с – расчетный расход холодной воды, определяемый по формуле(2.3), м 3 /с;

1 – длина расчетного участка трубопровода, м;

i = h₁/l – гидравлический уклон (удельная линейная потеря напора),м/м.

Величина А₁ определяется по формуле:

Значения величины А рассчитаны и приведены в таблицах [2, 6].

Значения произведения (1000i) в формуле (2.15) рассчитаны и приведены в таблицах [2, 5].

2.8 Выбор счетчика воды и определение потерь напора в нем

Для учета количества и расхода воды на вводе в здание в составе водомерного узла устанавливается скоростной счетчик воды. Скоростные счетчики воды бывают:

– крыльчатыетипа ВСКМ, ГОСТ 6019-83;

– турбинные типа СТВ, ГОСТ 14167-83.

Крыльчатые счетчики изготавливают диаметром условного прохода 15-50 мм; турбинные – 65-250 мм.

Диаметр условного прохода счетчика следует выбирать исходя из среднечасового расхода холодной воды за сутки наибольшего водопотребления. Этот расход не должен превышать эксплуатационный расход воды, принимаемый по таблице 4 [1].

Средний часовой расход холодной воды за сутки наибольшего водопотребления определяется по формуле:

q с _u – норма расхода холодной воды потребителем в сутки наибольшего водопотребления, л/сут; принимается по заданию (в общем случае – по Приложению И [1]);

U – общее количество потребителей (жителей) определяется по формуле (2.1);

Т – время потребления воды (T = 24), ч;

1000 – коэффициент пересчета (1 м 3 =1000 л).

Потери напора в счетчике определяются по выражению [1]:

q c – расчетный расход воды, м 3 /ч; определяется по формуле (2.3). Расчетные параметры счетчиков воды приведены в таблице 4 [1]. Потери напора в крыльчатых счетчиках не должны превышать 2,5 м, а в турбинных –1 м [1].

При конструировании водомерногоузла необходимо использовать его типовые схемы [2].

Определение диаметров труб и потерь напора в сети

Графы 9, 10, 11 (табл. 1) заполняются с использованием таблиц для гидравлического расчета стальных водопроводных труб (табл. 8). При выполнении расчета рекомендуется проверить возможность применении труб одного диаметра на всю высоту стояка и магистральной линии.

Диаметры труб и потери напора на единицу длины (1000i) на каждом расчетном участке следует определять методом интерполяции по табл. [2], выборка из которых приведена в табл. 8, по величине q_в с учетом допустимых расчетных скоростей в элементах сети, которые в трубопроводах водопроводной сети не должны превышать 3 м/с СНиП 2.04,01-85 § 7.6 Экономические скорости следует принимать 0,9–1,2 м/с но не более 1,5 м/с.

В примере q_в1-2 = 0,093 л/с, данный расчетный расход в табл.8 находится между табличными

расходами = 0,08 л/с и = 0,10 л/с;

скоростями = 0,47м/с и = 0,59м/с;

потерями напора на единицу длины (1000i)

Разность между верхним и нижним пределом табличных расходов

Разность между действительным расчетным расходом q_в и ближайшим табличным расходом q ₁ табл

0,093 – 0,08 = 0,013 л/с.

Далее интерполируем искомую скорость из соотношений

V = 0,47 + (0,59 – 0,47) × 0,013/0,02 = 0,545 м/с,

потери напора на единицу длины 1000_i

66,9 + (102,2 – 66,9) × 0,013/0,02 = 88,5.

Аналогичным способом определяют ближайшие допустимые скорости и, соответственно, диаметры труб и потери напора на трение для остальных расчетных участков и заполняют графы 9, 10, 11 табл. 1. Графу 12 получают умножением графы 2 на графу 11.

Результатом заполнения графы 12 табл. 1 явится суммарная величина потерь на трение на линии ввода Н_вв (см. расчетные участки табл. 1 «11-ВУ и ВУ-ввод»).

Лабораторная работа № 5 определение потери напора в прямой трубе

V – средняя скорость;

l – коэффициент гидравлического сопротивления трения (коэффициент Дарси).

где D – абсолютная шероховатость, n – кинематический коэффициент вязкости жидкости.

При расчетах сначала определяют область гидравлического сопротивления, затем выбирают расчетную формулу.

Вид функции (2) впервые был установлен опытами Никурадзе, выполненными для плотной, однородной, равномерной шероховатости из песка, нанесенной на внутреннюю поверхность круглых труб.

Были определены следующие области сопротивления:

1) область ламинарного течения Re 500

Расчетная формула Никурадзе

или формула Шифринсона

Коэффициент сопротивления lв этой области обычно имеет значенияl= 0,02…0,05.

Целью настоящей работы является:

1. Определение потери напора h_l при движении воды расчетным путем по формуле Дарси – Вейсбаха и опытным путем по показаниям пьезометров.

2. Сравнение полученных результатов и определение погрешности опыта.

2. Описание установки

Напорный бак 1 (рис. 8) присоединен к водопроводной сети 2 с помощью крана К₁. Труба 3 соединяет напорный бак с канализацией, предохраняя его от переполнения. Две горизонтально расположенные трубы 4 и 5 одинакового диаметра (d₁=d₂=20 мм) сделаны из разных материалов имеющих разную величину эквивалентной шероховатости (Δ=0,02 мм и Δ=0,2 мм). На конце каждой из этих труб установлены регулировочные краны К₂ и К₃, позволяющие изменять расход воды. Бак 6 имеет перегородку, которая делит его на два отсека С и М (сливной и мерный).

В зависимости от положения гибкого шланга, надетого на трубу, поток из трубы направляется либо в сливной С, либо в мерный М отсек бака. Количество воды в мерном отсеке определяется с помощью водомерного стекла 7. На стенде над трубами расположена панель измерительных инструментов 8, на которой расположены пьезометры, измеряющие потери напора h_l на соответствующих рабочих участках трубы l_АВ на трубе 4 и l_A’B’ на трубе 5.

3. Порядок выполнения работы.

Испытания проводить отдельно для трубы 4, затем для трубы 5.

Установить постоянный напор в баке 1 (), регулируя расход в трубе кранами(или) и краномна входе в напорный бак.

Определить расход воды Q, замеряя его объемным методом,

где t – время заполнения объема W мерного бака 6.

Определить среднюю скорость живого сечения

где – площадь живого сечения.

По измеренной температуре T в мерном баке 6 определить коэффициент кинематической вязкости (см. табл. 7) и вычислить число Рейнольдса:

Лабораторная работа №3. ПОТЕРИ НАПОРА ПО ДЛИНЕ ТРУБОПРОВОДА

Цель работы: определение значения коэффициента гидравлического сопротивления (трения) λ (коэффициента Дарси) и сопоставление его с величиной, рассчитанной по эмпирической формуле.

1. Освоить на практике способ определения режима течения жидкости по трубопроводу.

2. Усвоить основные соотношения при расчете потерь напора: формулы Дарси-Вейсбаха, Блазиуса, Альтшуля, Пуазейля, Шифринсона.

3. Освоить методику расчета потерь по длине для гидравлических гладких и шероховатых труб на различных режимах течения.

Потери напора (давления) в трубопроводах гидросистем принято разделять на местные потери и потери по длине. Правильный расчет потерь при проектировании гидросистем важен, поскольку определяет:

• работоспособность гидропривода, гидросистем;

• коэффициент местного действия гидросистемы станка, робота или другой машины;

• тепловой баланс в гидросистеме станка, энергоустановки, теплообменнике;

• экономию энергетических и материальных ресурсов.

Потери по длине играют существенную роль в системах тепло- и энергосбережения, подачи топлива, в гидросистемах автоматических линий и пр.

Потери по длине – это потери, обусловленные вязким трением частиц жидкости между собой и о стенки трубопроводов при равномерном течении в прямых трубах постоянного сечения.

Как лабораторным путем определить потери на каком либо участке трубы

Казанский государственный технологический университет

Лабораторная работа №3

Определение потерь напора в прямой цилиндрической трубе

Цель работы: 1) определение потерь напора непосредственно из опыта при различных скоростях движения воды;

2) определение потерь напора по длине расчетным путем; 3) сравнение полученных опытных значений с вычисленными.

Описание установки: (рисунок на последней странице) установка состоит из центробежного насоса 14, бака 1, трубопровода, включающего прямую горизонтальную круглую стальную трубу 2, регулировочных задвижек 11 и 13. Потери напора в трубе измеряются дифференциальным манометром 4, присоединенным к начальному и конечному сечениям исследуемого участка трубы с помощью пьезометрических колец и импульсных трубок. Расход протекающей через трубопровод воды регулируется задвижкой 11 и определяется с помощью водомера 3 и секундомера.

Сущность работы: гидравлические потери напора по длине (путевые потери) при течении жидкости в прямой трубе обусловлены трением слоев жидкости друг о друга и о стенки канала и определяются по формуле Дарси-Вейербаха:

Источник