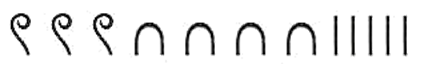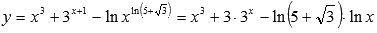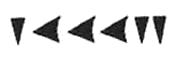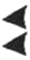к какому виду относится римская система счисления

Системы счисления. Непозиционные системы счисления.

В непозиционных системах счисления величина, обозначающая цифру, не зависит от положения в числе. К тому же, система может накладывать ограничения на расстановку цифр, например, чтобы цифры располагались по убыванию.

Существуют такие непозиционные системы счисления:

— Единичная система счисления,

— Пятеричная система счисления (Счёт на пятки́),

— Древнеегипетская система счисления,

— Вавилонская система счисления,

— Алфавитные системы счисления,

— Еврейская система счисления,

— Греческая система счисления,

— Римская система счисления,

— Система счисления майя,

Рассмотрим некоторые из, приведенных выше, систем счисления.

Единичная система счисления.

С первых попыток научиться считать у людей возникла необходимость записи чисел. Сначала это было легко — зарубка либо черточка на любой поверхности отвечала за один предмет. Таким образом возникла первая система счисления — единичная.

Число в единичной системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.

В более позднее время для упрощения восприятия больших чисел, эти знаки стали группировать по три или по пять. Далее равнообъёмные группы знаков начали заменять новым знаком — так возникли прообразы современных цифр.

У данной системы есть значительные недостатки — чем больше число, тем длиннее строка из палочек. Кроме того, существует большая вероятность в записи числа, пропустив или случайно дописав палочку.

Изначально в счете использовали пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.

Древнеегипетская десятичная система счисления.

В Древнем Египте использовали свои символы (цифры) для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Вот некоторые из них:

Почему мы ее называем десятичной? Как указано выше — люди начали группировать символы. В Египте — решили группировать по 10, оставив без изменений цифру “1”. Здесь, число 10 называется основанием десятичной системы счисления, а все символы — представление числа 10 в определенной степени.

Числа в древнеегипетской системе счисления записывали, в виде комбинаций таких символов, и все они повторялись не больше 9 раз. Результатом было сумма элементов числа. Этот метод получения значения свойственен каждой непозиционной системе счисления. Для примера посмотрите на запись числа 345:

Вавилонская шестидесятеричная система счисления.

В вавилонской системе счисления использовали только 2 символа: “прямой” клин — для единиц и “лежащий” — для десятков. Для определения значения числа нужно изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. Для примера посмотрим на число 32:

Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной системы счисления.

Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а значения больше 59 — в позиционной с основанием 60. Например, число 92:

Запись числа была не конкретной, так как не было цифры, которая обозначала бы нуль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа они ввели новый символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:

Значит, число 3632 записывают так:

Шестидесятеричная вавилонская система — первая система счисления, которая частично основана на позиционном принципе. Эту систему счисления используют и сейчас, например, для определения времени — час состоит из 60 минут, а минута из 60 секунд.

Римская система счисления.

Римская система счисления немного похожа с египетской. Здесь для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используют заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.

Способы определения значения числа:

Источник

Римская система счисления

Римские цифры — цифры, использовавшиеся древними римлянами в своей непозиционной системе счисления.

Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.

Римские цифры появились около 500 лет до нашей эры у этрусков.

Содержание

Цифры

Число	Римское обозначение
1	I
5	V
10	X
50	L
100	C
500	D
1000	M

Для закрепления в памяти буквенных обозначений цифр в порядке убывания существует мнемоническое правило:

Соответственно M, D, C, L, X, V, I

Примеры

Число	Римское обозначение
0	отсутствует
4	IV (иногда IIII)
8	VIII
9	IX
31	XXXI
46	XLVI
99	IC
666	DCLXVI
1668	MDCLXVIII
1989	MCMLXXXIX
3999	MMMCMXCIX
2009	MMIX

Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.

Пример: число 1988. Одна тысяча M, девять сотен CM, восемьдесят LXXX, восемь VIII. Запишем их вместе: MCMLXXXVIII.

Существует «сокращённый способ» для записи больших чисел, таких как 1999. Он не рекомендуется, но иногда используется для упрощения. Отличие состоит в том, что для уменьшения цифры слева от неё может писаться любая цифра:

Применение

В русском языке римские цифры используются в следующих случаях.

В других языках сфера применения римских цифр может иметь особенности, например, в западных странах римскими цифрами иногда записывается номер года.

Расширение

Римские цифры предоставляют возможность записывать числа от 1 до 3999 (MMMCMXCIX). Для решения этой проблемы были созданы [кто?] расширенные римские цифры.

Юникод

Римские цифры в Юникод

Код	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Значение [4]	1	2	3	4	5	6	7	8	9	10	11	12	50	100	500	1 000
U+2160	Ⅰ 2160	Ⅱ 2161	Ⅲ 2162	Ⅳ 2163	Ⅴ 2164	Ⅵ 2165	Ⅶ 2166	Ⅷ 2167	Ⅸ 2168	Ⅹ 2169	Ⅺ 216A	Ⅻ 216B	Ⅼ 216C	Ⅽ 216D	Ⅾ 216E	Ⅿ 216F
U+2170	ⅰ 2170	ⅱ 2171	ⅲ 2172	ⅳ 2173	ⅴ 2174	ⅵ 2175	ⅶ 2176	ⅷ 2177	ⅸ 2178	ⅹ 2179	ⅺ 217A	ⅻ 217B	ⅼ 217C	ⅽ 217D	ⅾ 217E	ⅿ 217F
Значение	1 000		5 000		10 000		–	–	6		50		50 000		100 000
U+2160! U+2180	ↀ 2180		ↁ 2181		ↂ 2182		Ↄ	ↄ	ↄ		ↄ		ↄ		ↄ

Символы в диапазоне U+2160—217F присутствуют только для совместимости с другими стандартами, которыми определены эти символы. В обиходе применяются обычные буквы латинского алфавита. Отображение таких символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы.

Примечания

Полезное

Смотреть что такое «Римская система счисления» в других словарях:

Римская система счисления — непозиционная система счисления, в которой для записи чисел используются буквы латинского алфавита: I означает один ; V означает пять ; X означает десять ; L означает пятьдесят ; C означает сто ; D означает пятьсот ; M означает тысяча ; Для… … Финансовый словарь

Система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Позиционная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Троичная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Унарная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Двоичная система счисления — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия

Двенадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Кириллическая система счисления — Башенные часы с кириллическими числами в Суздале … Википедия

Двадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Шестидесятеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Источник

Римская система счисления Ⅷ

Здравствуйте, на этой странице разберем римскую систему счисления. Здесь мы поговорим про основные определения, её значение в информатике и других науках, рассмотрим сферы, где она применяется на данный момент. Поговорим про её перевод в десятичную систему.

Краткий исторический экскурс

Первые достоверные упоминания о римской системе счисления датируются от пятисотых годов до нашей эры. Точных обстоятельств, при которых возникла нотация, никто не знает. Однако мы можем опираться на несколько версий.

Например, вот одна из них: цифры от 1 до 3 записывались с помощью палочек (I, II, III). Это говорит, что Римская нумерация берет свое начало от унарной (единичной системы). Она является простейшей и примитивнейшей нумерацией, в ней был только один знак, который обозначал единицу. Однако тогда было непонятно, как возникли другие символы. На этот счет есть более интересная версия.

Некоторые считают, что формат появился благодаря методам пальцевого счета. Так значения от одного до четырех отображались пальцами от указательного до мизинца. Число 5 же (V) – угол между указательным и большим пальцем, а десять соответствует двум рукам, с помощью которых показывается знак X.

Но и с этой версией не все так гладко. В ней считается, что римляне переняли обозначения у древних этрусков. Однако те, в свою очередь, читали свои записи справа налево, в то время как жители Рима читали их слева направо. Так что история происхождения исчисления и по сей день остается неразгаданной. Перейдем к понятиям.

Основные положения

Римское исчисление – является непозиционной системой счисления, в которой для отображения чисел используются буквы латинского алфавита, такие как I, V, X, L, M, C, D. Чтобы понять, что значит каждая из них, приведем ниже небольшую табличку.

Перевод десятичных чисел в римскую систему счисления и обратно

Чтобы осуществить перевод необходимо усвоить несколько простых правил, после изучения которых, Вы сможете с легкостью перевести любое значение. Вот что вам необходимо усвоить:

Калькулятор в РСС

Введите величину в дес.формате

Сгенерировать случайную

Достоинства и недостатки в сравнении с позиционными отображениями

К плюсу римской нотации можно отнести, что с помощью неё легко производить арифметические действия с маленькими значениями. Минусов же у неё намного больше, ими являются все недостатки непозиционных форматов, такие как:

Все эти минусы привели к тому, что на данный момент главенствующим является более совершенный позиционный формат (например, позиционный двоичный или десятеричный способ отображения количественных величин). Именно он используется в точных науках – математике и информатике. Однако нотация кое-где применяется и сейчас.

Где применяется

Заключение

Вот и всё, Вы познакомились с непозиционной римской системой счисления. Теперь Вы знаете основные положения, её историю происхождения, значение в информатике, а так же как осуществлять перевод значений в десятичном формате. Тема достаточно интересная, при возникновении вопросов – задавайте их в комментариях.

Источник

Информатика

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Развиваясь, древний человек стал испытывать потребность в способах выражения количества. Подсчет убитых животных, количество врагов или соседей – причин становилось все больше. Сначала люди использовали только понятия «один», «много». После стали использовать понятие «пара», чтобы обозначить два предмета, это намного облегчило жизнь.

Постепенно перешли к использованию подручных средств – пальцев на руках и ногах, зарубок на коре дерева, кости животного или узелков на канате. Именно такие примитивные «счетные машины» позволили через тысячи лет узнать, что предки умели не просто считать, но даже умудрялись фиксировать результаты подсчета.

Кроме зарубок и узелков появилась потребность в символах, выражающих большее количество чего-либо, чем «один». Тогда были придуманы первые знаки для выражения больших значений. Так, египтяне, использовали знаки для цифр 1, 5, 10. Число 324 в их системе выглядело так:

А описание чисел при помощи специальных знаков и является системой счисления.

Системы счисления – виды, особенности

Система счисления (СС) – способ выражения чисел при помощи специальных правил и знаков, которые называются цифрами.

Все существующие системы делят на 2 группы:

Чтобы выразить число 475, достаточно по порядку написать 3 символа, 475, выражая 5 единиц, 7 десятков и 4 сотни.

К этой группе также относятся СС с различными основаниями (2,8,16).

Еще одна особенность – чтобы выразить число и не использовать сотни символов, применяется прибавление и вычитание. Написать 475 римскими знаками можно так CCCCXXXXXXXIIIII, но это нерационально. Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.

Правильным считается тот вариант, при котором получается меньше символов.

Интересно. Первой позиционной СС была вавилонская и была она шестнадцатиричная! А в 19 веке использовали двенадцатеричную СС.

Алфавит СС – знаки, которые используются для обозначения цифр.

Основание – количество знаков, которыми кодируются числа. Еще оно показывает отличие между цифрами на разных позициях. Основание – целое число, начиная с 2.

Важно. Если в тексте идет речь о различных системах, то чтобы уточнить, какая используется основа, ставится подстрочный знак: 1254₈, 01100111₂. Примеры? Если же обозначения нет, по умолчанию это десятичная (12549).

Разряд – положение, позиция обозначения цифры в числе. Пример?

Непозиционные СС, их особенности

Первоначально древние люди ставили отметки (черточки-зарубки, точки), чтобы обозначить количество того или иного предмета. Отклики этого подхода все еще встречаются (полоски у военных, счетные палочки).

Постепенно от единиц они переходили к группам предметов по 3, 5, 10 единиц. Постепенно такие группы стали обозначаться определенными символами, что позволило сократить размер записи.

Римская СС

В ней определенным цифрам отвечают латинские буквы. Их сумма и будет числом.

Основные рекомендации при пользовании римскими цифрами:

Таблица римских цифр

Недостаток этой СС в том, что для больших чисел недоступны операции сложения или другие, ещё она сложная и громоздкая. Зато римские цифры отлично вписались там, где нужна нумерация и эстетика: циферблаты, номера глав, списки, серии документов.

Основные позиционные СС, правила перевода

Двоичная система счисления

Систему, на которой основывается работа компьютеров, придумал гениальный немецкий ученый Г.В. Лейбниц (еще до 19 века!). Он придумал и описал СС, в которой все вычисления проводятся при помощи двух простейших символов – 0 и 1.

Компьютер, как механическое устройство, получает команды в виде двоичной кодировки. Он не в силах понять сложные задания, человеческую речь, музыку или тысячи оттенков, а переводя/кодируя всю необходимую информацию при помощи 0 и 1 (сеть, отсутствие сети), можно передать ему любые команды или информацию. Естественно, такие задания выглядят как огромные массивы двух знаков.

Алгоритм перевода чисел из десятичной в двоичную систему:

Этот порядок действия позволят переводить в любую позиционную СС. В данном случае, основа – 2, остаток 2 +7*10 1 +9*10 0 = 579₁₀.

Обычно мы пользуемся свернутой формой записи чисел, то есть без разбивки на разряды и умножения на основу.

А чтобы было легче, пользуются готовой таблицей степеней 2.

Альтернативный способ преобразования для гуманитариев

Для начала нужно написать степени двойки, начиная с самой большой:

Далее нужно отнимать от числа максимальную степень двойки и напротив нее ставить 1, если есть в исходном варианте или 0, если его нет.
Перевод числа 579

Если же оно на 1 больше, то число будет начинаться и заканчиваться на 1, а внутри – сплошные 0.

Основой такой системы является 8, а числа восьмеричной системы 0-7. Данная система счисления является позиционной и целочисленной. Применяется в сферах, связанных с цифровыми технологиями, особенно в Linux-программном обеспечении (права доступа, исполнения).

Пример: Перевести 579₈ из десятичной в восьмеричную систему счисления:

Обратный перевод из восьмеричной СС в десятичную:

1103₈ = 1∙8 3 +1∙8 2 +0∙8 1 +3∙8 0 = 512+64+0+3 = 579₁₀

Альтернативный вариант таблицы степеней

Шестнадцатеричная СС

Это целочисленная система с основанием 16 (символы шестнадцатеричной системы счисления 0-9 и буквы A – F). Используется в реализации компьютерного программирования и документации на низком уровне, так как 8-битный байт, для записи которого удобно использовать 2 цифры из шестнадцатеричной системы.

Стандарт Юникод использует 4 и более символов 16-ой СС.

Для записи цвета из красного, зеленого и синего (R, G и B) также используют эту систему.

Алгоритм преобразования чисел в 16СС

Способ преобразования аналогичный предыдущим – расписывание числа как многочлена с учетом степеней 16. Для этого число делится на 16, в итоге – перечень остатков от деления, записанных наоборот.

В сети есть калькуляторы, способные выполнять преобразование чисел в различные СС и обратно (некоторые даже с детальным описанием процесса).

Арифметика для 2СС

Принципы выполнения простейших арифметических операций одинаковы для любых позиционных систем, независимо от основы:

Особенности арифметики СС с разными основами:

Примеры арифметических операций:

Для удобства разработаны готовые таблицы сложения в различных системах:

Сложение в 8-ой СС в 16СС

С их помощью можно быстро суммировать в различных СС.

Сложение для разных СС на примере 15 и 6:

Если необходимо сложить числа из разных систем, их приводят к одной основе. Самым простым вариантом будет перевод в десятичную систему, решение простого примера и перевод результата в любую из систем.

Рассмотрим сумму 43₈ и 56₁₆. Результат можно выразить в любой СС, но проще привести к 8- или 16-ричной:

Переводим число 56 в восьмеричную через двоичную:

Умножение в 8-ой СС

Сравнение систем

СС могут быть с произвольной основой, но популярны 2,8,10,16-ые.

Сравнительная таблица разных систем счисления:

Перевод числа 75 в разные системы:

Правила перевода из двоичной, восьмеричной и шестнадцатеричной в 10СС:

Исходный вариант следует разделить на тройки цифр, с крайней справа. Если не хватает, старший разряд дополнить 0. Далее под каждой триадой ставится подходящий символ из 8‑ой системы.

Рассмотрим перевод на примере числа 579, которое соответствует 1001000011₂

Правила перевода из двоичной в шестнадцатеричную систему счисления:

Число разбивается по 4 знака, начиная справа (с меньшего разряда). Если не будет хватать символов у старшего разряда, тетраду дополняют нулями.

Сравнительный перевод дробей в СС

Чтобы перевести правильные дроби из 10-ой СС в другие позиционные, следует придерживаться правила, которое хорошо видно на примере перевода числа 0,35:

Удобно писать над каждой цифрой порядок, а дальше ее умножить на основу СС в степени разряда.

Перевод целых и дробей в 2СС, 8СС, 16СС:

Таблицы истинности

При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.

Основные логические операции

Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.

Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:

Фрагмент таблицы истинности для конъюнкции.

Так выражаются условия для всех логических операций.

Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.

Источник