к какому типу относится таблица табель успеваемости
Ответы Учебник Информатика 9 класс — §1.4.Табличные информационные модели
Ответы (решебник) к учебнику по Информатике — 9 класс, параграф 1.4 — Босова Л.Л., Босова А.Ю. , задания 1-10
Глава 1. МОДЕЛИРОВАНИЕ И ФОРМАЛИЗАЦИЯ
§1.4.Табличные информационные модели ГДЗ, Информатика 9 класс Босова ответы на «Вопросы и задания»
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Какие преимущества обеспечивают табличные информационные модели по сравнению со словесными описаниями? Приведите пример
Преимуществом табличной информационной модели является компактность и легкообозримость.
3. Примеры табличный информационных моделей:
а) на уроках в школе: таблица умножения, таблица Менделеева, расписание уроков, школьный дневник и журнал
б) в повседневной жизни: календарь, расписание движения автобусов
4. К какому типу относится таблица «Табель успеваемости», расположенная в конце вашего дневника?
Таблица «Табель успеваемости» является таблицей «объект-свойство».
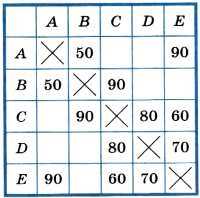
5. Узнайте, в каких случаях в ячейку таблицы ставится знак «х». Почему мы использовали этот знак в таблице (пример 2)?
Этот знак(х) мы ставим тогда, когда значение в этой ячейке невозможно и оно пустое.
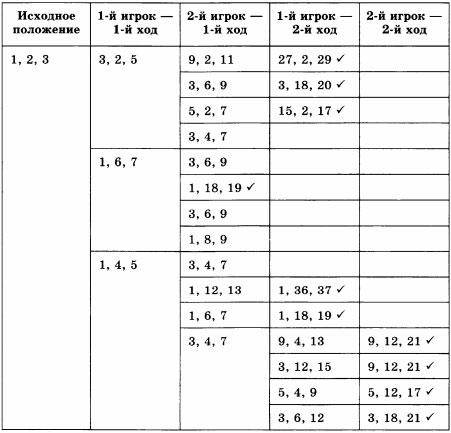
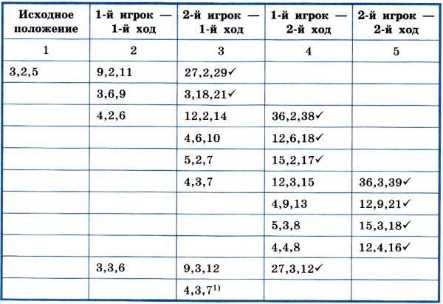
6. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 1 камень, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 17. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Рассмотрим все варианты ходов первого игрока. Различных вариантов у него оказывается 3, так как 1 · 3 = 3 и 1 + 2 = 3. Поэтому во 2-м столбце заполним только 3 ячейки.
Пусть после хода 1-го игрока в кучах оказалось 3 и 2 камня. Рассмотрим все варианты ходов 2-го игрока. Из таблицы видно, что только один из его ходов не позволит выиграть первому игроку своим вторым ходом. Это ситуация, когда в кучах окажется по 3 и 4 камня. Вернемся к ее рассмотрению чуть позже.
Первый игрок не должен сделать ход, приводящий к ситуации, когда в кучах окажется 1 и 6 камней, так как в этом случае второй игрок получает возможность выиграть, утроив число камней во второй куче.
Если после хода 1-го игрока в кучах оказалось 1 и 4 камня, то второй игрок не сможет добиться выигрыша своим первым ходом. Но два его хода, в результате которых в кучах окажется по 3 и 4 камня, не позволят выиграть первому игроку своим вторым ходом. Рассмотрим эту ситуацию подробно.
Представим все варианты второго хода первого игрока, если в результате хода второго игрока в кучах оказалось 3 и 4 камня. Ни один из ходов первого игрока не может привести к победе, но такая возможность появляется у второго игрока.
Ответ:
При безошибочной игре соперников побеждает второй игрок. У него есть шанс выиграть первым ходом. Иначе его первый ход должен быть таким, чтобы в кучах оказалось 3 и 4 камня.
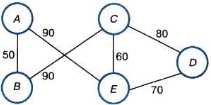
7. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость перевозок между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Стоимость перевозок по маршруту складывается из стоимостей перевозок между соседними станциями. Перевозки между населёнными пунктами А, В, С, В, Е осуществляют три компании, представившие стоимость своих услуг в табличной форме. Какая компания обеспечивает минимальную стоимость перевозок из А в В?
Для большей наглядности перейдем от таблиц к графам:
Минимальная стоимость у 1 компании
ACB = 3 + 4 = 7
Минимальная стоимость у 2 компании
ACB = 3 + 4 = 7
AECB = 1 + 2 + 4 = 7
Минимальная стоимость у 3 компании
ACB = 3 + 4 = 7
AECB = 4 + 2 + 4 = 10
AEB = 4 + 2 = 6
Ответ:
Третья компания.
8. Соревнования по плаванию были в самом разгаре, когда стало ясно, что первые четыре места займут мальчики из пятёрки лидеров. Их имена: Валерий, Николай, Михаил, Игорь, Эдуард, фамилии: Симаков, Чигрин, Зимин, Копылов, Блинов (имена и фамилии названы в произвольном порядке). Нашлись знатоки, которые предсказали, что первое место займёт Копылов, второе — Валерий, третье — Чигрин, четвёртое — Эдуард. Но ни один из ребят не занял того места, какое ему предсказывали. На самом деле первое место завоевал Михаил, второе — Симаков, третье — Николай, четвёртое — Блинов, а Чигрин не попал в четвёрку сильнейших. Назовите имя и фамилию каждого из лидеров.
Прогноз
1. Копылов
2. Валерий
3. Чигрин
4. Эдуард
5. —
Результат
1. Михаил
2. Симаков
3. Николай
4. Блинов
5. Чигрин
Исходя из результата фамилия Михаила не Симаков, не Блинов и не Чигрин. Исходя из прогноза так же не Копылов. Значит, Михаил Зимин — 1 место.
Валерий не Симаков и не Чигрин. Значит, Валерий Блинов — 4 место.
Эдуард не Блинов, не Чигрин, Эдуард Симаков — 2 место.
Остались фамилии Чигрин, Копылов и имена Николай, Игорь. Чигрин так и остался в прогнозе в результате под одинаковым обозначением (фамилией), значит, имя Николай принадлежит Николаю Копылову — 3 место.
Чигрин Игорь — 5 место.
Ответ:
Михаил Зимин,
Эдуард Симаков,
Николай Копылов,
Валерий Блинов,
Игорь Чигрин.
9. В Норильске, Москве, Ростове и Пятигорске живут четыре супружеские пары (в каждом городе — одна пара). Имена этих супругов: Антон, Борис, Давид, Григорий, Ольга, Мария, Светлана, Екатерина. Антон живёт в Норильске, Борис и Ольга — супруги, Григорий и Светлана не живут в одном городе, Мария живёт в Москве, Светлана — в Ростове. В каком городе живёт каждая из супружеских пар?
Антон живет в Норильске, Светлана — в Ростове, Мария — в Москве.
Значит Борис и Ольга живут в Пятигорске.
Светлана и Георгий не живут в одном городе и это значит, что Георгий живет с Марией в Москве.
Остались Давид и Екатерина. Екатерина живет с Антоном в Норильске, а Давид живет со Светланой в Ростове.
Ответ:
Антон и Екатерина проживают в Норильске,
Григорий и Мария — в Москве,
Давид и Светлана — в Ростове,
Борис и Ольга — в Пятигорске.
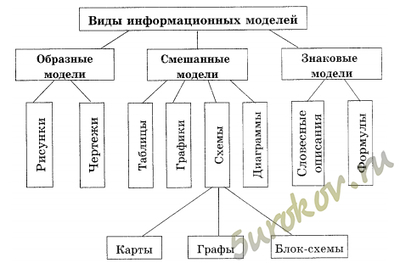
10. Постройте граф, отражающий разновидности информационных моделей
На этой странице размещен вариант решения заданий с страниц учебника по информатике за 9 класс авторов Босова. Здесь вы сможете списать решение домашнего задания или просто посмотреть ответы. ГДЗ
Литература: Учебник по Информатике, 9 класс. Автор: Босова Л.Л., Босова А.Ю. Издательство: Бином. Год: 2016, 2017
К какому типу относится таблица табель успеваемости
Вычислительными будем называть такие таблицы, в которых значения некоторых свойств вычисляются с использованием значений других свойств из этой же таблицы.
Таблица 2.19
Подарочный набор для первоклассника
| Товар | Цена, руб | . Количество | Стоимость, руб. |
| Тетрадь, 12л., клетка | 3 | 10 | 30 |
| Тетрадь, 12 л., линейка косая | 2,5 | 10 | 25 |
| Альбом для рисования, 8 л. | 5 | 4 | 20 |
| Карандаши цветные «Зарница», 6 цв. | 20 | 1 | 20 |
| Авторучка | 5 | 6 | 30 |
| Карандаш простой | 1 | 6 | 6 |
| Цветная бумага, 8 цв. | 12 | 2 | 24 |
| Итого: | 39 | 155 |
Эта таблица относится к типу ОС. Значения в графе «стоимость» вычислены по формуле: цена х количество.
Последняя строка этой таблицы называется итоговой. Она предназначена для записи итогов. Итоговая строка имеет заголовок «Итого» или «Всего».
В ячейках итоговой строки размещают суммы чисел из соответствующих граф. Но эти суммы должны иметь смысл. Так, если сложить все числа в графе «Количество», то мы узнаем общее число предметов, входящих в подарочный набор. Общая стоимость набора находится суммированием всех чисел, стоящих в графе «Стоимость». А вот сумма по графе «Цена» не имеет никакого смысла.
Собираясь на пляж, веселые человечки решили запастись прохладительными напитками. Незнайка взял с собой 2 литра кваса, 1 литр газировки и 1 литр малинового сиропа, Пончик — 3 литра газировки и 2 литрг го сиропа, Торопыжка — 2 литра газировки, доктор Пилюлькин — 1 литр кваса и 1 литр касторки.
Сколько литров напитков каждого вида взяли все человечки вместе?
Сколько всего литров напитков взял с собой каждый из человечков?
Сколько всего литров напитков взяли все человечки вместе?
Представим имеющуюся информацию о парах объектов классов «человечек»
— «напиток» в таблице типа ООО. В этом случае свойством пары объектов будет количество (в литрах) напитка, запасенного человечком.
| Напиток | Человечек | ||||
| Незнайка | Пончик | Торопыжка | Пилюлькин | Всего ; | |
| Квас,л | 2 | 0 | 0 | 1 | 3 |
| Газировка, л | 1 | 3 | 2 | 0 | 6 |
| Сироп, л | 1 | 2 | 0 | 0 | 3 |
| Касторка, л | 0 | 0 | 0 | 1 | 1 |
| Итого: | 4 | 5 | 2 | 2 | 13 |
Ответ на первый вопрос находится в итоговой графе таблицы. Ответ на второй вопрос — в итоговой строке. Ответ на третий вопрос находится в нижней правой ячейке — на пересечении итоговой строки и итоговой графы.
Обратите внимание, что последнее число может быть получено двумя способами. Узнать, сколько всего напитков взяли с собой человечки, можно, если сложить количество напитков, взятых Незнайкой, Пончиком, Торопыжкой и Пилюлькиным (суммирование по итоговой строке). Это же число будет получено, если сложить взятое человечками количество кваса, газировки, малинового сиропа и касторки (суммирование по итоговой графе). Эту особенность числа, стоящего в правой нижней ячейке таблицы, можно использовать для контроля своих вычислений.
Сколько монет истратил на покупку напитков каждый человечек?
Сколько монет затрачено на покупку напитков каждого вида?
Сколько потрачено денег всеми человечками вместе?
У нас появилось дополнительное свойство «цена», которое характеризует не пару объектов, а относится к одному объекту этой пары. Можем строить таблицу типа ОСО. Для этого видоизменим таблицу 2.20: правее боковика добавим графу «Цена». Для каждого человечка введем дополнительную графу «Стоимость». Итоговая графа тоже разбивается на две графы — «Количество» и «Стоимость»:
| Напит | Цена мон. | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего | |||||
| Кол- во, л | Ст-ть, мон | Кол- во, л | Ст-ть, мон | Кол- во, л | Ст-ть, мон | Кол- во, л | Ст-ть, мон | Кол- во, л | Ст-ть, мон | ||
| Квас | 1 | 2 | 2 | 0 | 0 | 0 | 0 | 1 | 1 | 3 | 3 |
| Газировка | 3 | 1 | 3 | 3 | 9 | 2 | 6 | 0 | 0 | 6 | 18 |
| Сироп | 6 | 1 | 6 | 2 | 12 | 0 | 0 | 0 | 0 | 1 | 18 |
| Касторка | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 2 |
| Итого: | 4 | 11 | 5 | 21 | 2 | 6 | 2 | 3 | 13 | 41 | |
Чтобы при вычислениях не путать литры с монетами, чуть видоизменим таблицу:
| Напитки | Цена, мон. | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего | |||||
| Кол- во, л | Ст-ть, мон | Кол- во, л | Ст-ть, мон | Кол- во, л | Ст-ть, мон | Кол- во, л | Ст-ть, мон | Кол- во, л | Ст-ть, мон | ||
| Квас | 1 | 2 | 2 | 0 | 0 | 0 | 0 | 1 | 1 | 3 | 3 |
| Газировка | 3 | 1 | 3 | 3 | 9 | 2 | 6 | 0 | 0 | 6 | 18 |
| Сироп | 6 | 1 | 6 | 2 | 12 | 0 | 0 | 0 | 0 | 1 | 18 |
| Касторка | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 2 |
| Итого: | 4 | 11 | 5 | 21 | 2 | 6 | 2 | 3 | 13 | 41 | |
Вычислительными будем называть такие таблицы, в которых значения некоторых свойств вычисляются с использованием значений других свойств из этой же таблицы.
Вычислительная таблица может содержать итоговую строку (графу). Итоговая строка (графа) имеет заголовок «Итого» или «Всего».
В ячейках итоговой строки (графы) размещают суммы чисел из соответствующих граф (строк). Важно, чтобы эти суммы имели смысл.
1. В какой жизненной ситуации могут оказаться полезными вычислительные таблицы? Приведите пример.
2. На что следует обращать внимание при заполнении итоговой строки (графы)?
Урок 5
§1.4 Табличные информационные модели
Ключевые слова:
• таблица
• таблица «объект—свойство»
• таблица «объект—объект»
В табличных информационных моделях информация об объектах представляется в виде прямоугольной таблицы, состоящей из столбцов и строк.
Вам хорошо известно табличное представление расписания уроков, в табличной форме представляются расписания движения автобусов, самолётов, поездов и многое другое.
Представленная в таблице информация наглядна, компактна и легкообозрима.
1.4.1. Представление данных в табличной форме
В качестве информационных моделей объектов, обладающих одинаковыми наборами свойств, как правило, используются таблицы типа «объект—свойство».
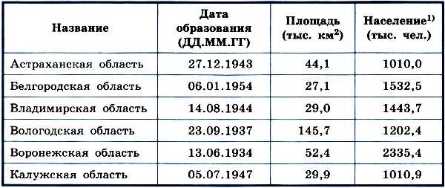
Например, информацию о регионах нашей страны можно представить с помощью таблицы, фрагмент которой приведён в табл. 1.1.
В этой таблице каждая строка содержит информацию об одном объекте — регионе; столбцы — отдельные характеристики (свойства) рассматриваемых объектов: название, дата образования, площадь и т. д. Такие таблицы могут содержать числовую, текстовую и графическую информацию.
Таблица 1.1
Регионы Российской Федерации
1) Численность населения приведена по результатам переписи населения России 2010 г.
Располагаете ли вы аналогичной информацией о своём регионе? Уточните информацию о современной численности населения вашего региона.
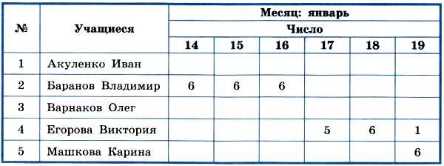
В таблицах типа «объект — объект» отражается взаимосвязь между объектами одного или нескольких классов. Например, в школьных журналах есть таблица «Сведения о количестве уроков, пропущенных обучающимися»; её фрагмент представлен в табл. 1.2.
Таблица 1.2
Сведения о пропусках уроков
В этой таблице отражена связь «количество пропущенных уроков» между объектами класса «Учащиеся» и объектами класса «Число».
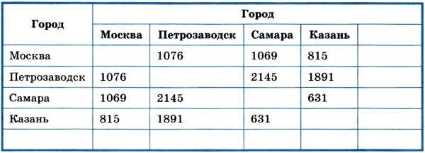
В таблице «Расстояния между городами» (табл. 1.3) представлены расстояния между парами объектов, принадлежащих одному классу «Город». Создайте эту таблицу в текстовом редакторе и добавьте в свободные строку и столбец информацию о своём населённом пункте.
Таблица 1.3
Расстояния между городами (км)
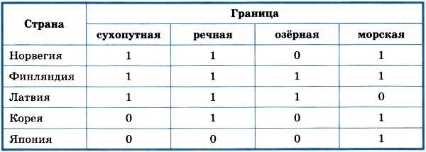
В форме таблицы «объект-объект» можно представить информацию о наличии границ (сухопутной, морской, озёрной, речной) России с другими странами; её фрагмент представлен в табл. 1.4.
Таблица 1.4
Граница Российской Федерации
Если граница соответствующего вида есть, то в нужную ячейку ставится 1, а если нет — 0.
Важная особенность этой таблицы состоит в том, что в ней фиксируются не количественные («Сколько?»), а качественные свойства (наличие/отсутствие связи между объектами).
1.4.2. Использование таблиц при решении задач
Рассмотрим несколько примеров задач, которые удобно решать с помощью табличных информационных моделей.
Пример 1. Два игрока играют в следующую игру. Перед ними лежат две кучи камней, в первой из которых 3 камня, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16. Кто выигрывает при безошибочной игре — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте. Ранее мы рассмотрели способ записи решения подобных задач с помощью дерева. Сейчас оформим решение в виде таблицы (табл. 1.5).
Таблица 1.5
Таблица игры
1) Вариант (как повторный) исключается из дальнейшего рассмотрения
Три числа в каждой ячейке таблицы обозначают соответственно количество камней в кучах и их сумму. В первом столбце зафиксировано распределение камней перед игрой (исходное положение).
Во втором столбце рассмотрены все возможные варианты ходов первого игрока; победить с первого хода он не может.
В третьем столбце рассмотрены имеющиеся выигрышные варианты ходов второго игрока (отмечены «галочкой»). При безошибочной игре первого игрока такие ситуации возникнуть не должны. Поэтому рассматриваем все возможные ходы второго игрока в случаях, когда у него нет выигрышного хода. Если получены одинаковые варианты, то все из них, кроме одного, исключаем из дальнейшего рассмотрения.
В четвёртом столбце отмечены имеющиеся выигрышные варианты второго хода первого игрока. При безошибочной игре второго игрока такие ситуации возникнуть не должны. Поэтому рассматриваем все возможные ходы первого игрока в случае, когда у него нет выигрышного хода.
В пятом столбце отмечены выигрышные ходы второго игрока, имеющиеся при всех вариантах хода первого игрока.
Таким образом, при безошибочной игре соперников побеждает второй игрок. Его первый ход должен быть таким, чтобы в кучах стало 4 и 3 камня.
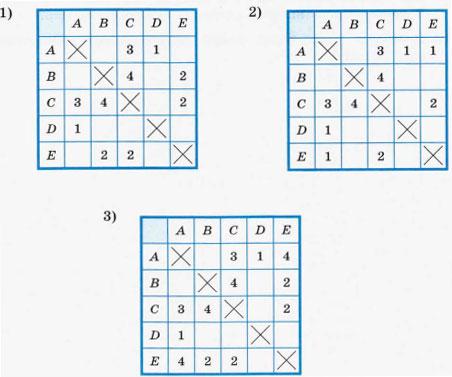
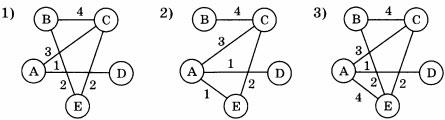
Пример 2. С помощью взвешенного графа на рис. 1.6, в представлена схема дорог, соединяющих населённые пункты А, В, С, D, Е. Построим таблицу, соответствующую этому графу (рис. 1.12).
Рис. 1.12. Весовая матрица
Если между парой населённых пунктов существует дорога, то в ячейку на пересечении соответствующих строки и столбца записывается число, равное её длине. Имеющиеся в таблице пустые клетки означают, что дорог между соответствующими населёнными пунктами нет. Построенная таким образом таблица называется весовой матрицей.
Для решения некоторых задач бывает удобно по имеющейся таблице строить граф. При этом одной и той же таблице могут соответствовать графы, внешне не похожие друг на друга. Например, рассмотренной выше таблице кроме графа на рис. 1.6, в соответствует граф на рис. 1.13.
Рис. 1.13. Вариант графа, представляющего схему дорог
Пример 3. Таблицы типа «объект—объект» удобно использовать для решения логических задач, в которых требуется установить взаимно однозначное соответствие между объектами нескольких классов. Рассмотрим задачу, в которой объекты связаны тремя парами отношений.
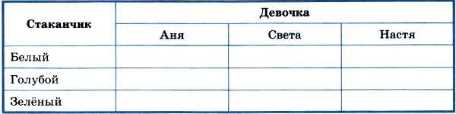
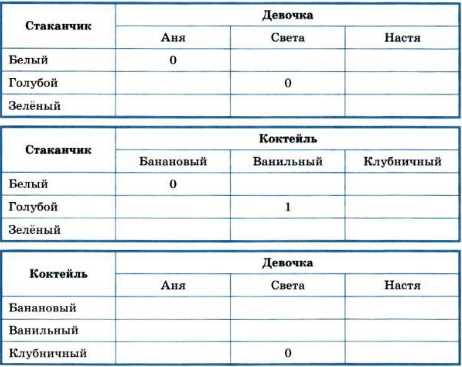
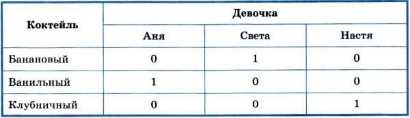
Три подружки — Аня, Света и Настя — купили различные молочные коктейли в белом, голубом и зелёном стаканчиках. Ане достался не белый стаканчик, а Свете — не голубой. В белом стаканчике не банановый коктейль. В голубой стаканчик налит ванильный коктейль. Света не любит клубничный коктейль.
Требуется выяснить, какой коктейль и в каком стаканчике купила каждая из девочек.
Создадим три следующие таблицы:
Отметим в таблицах информацию, содержащуюся в условии задачи:
Имеющейся во второй таблице информации достаточно для того, чтобы заполнить всю эту таблицу:
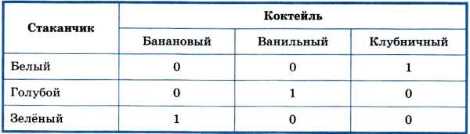
Используя факты, что Света купила не клубничный коктейль и что этот коктейль был налит в белый стаканчик, заполняем всю первую таблицу:
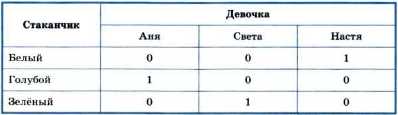
На основании информации в первой и второй таблицах можем заполнить всю третью таблицу:
Ответ: Аня купила ванильный коктейль в голубом стаканчике, Света — банановый коктейль в зелёном стаканчике, Настя — клубничный коктейль в белом стаканчике.
САМОЕ ГЛАВНОЕ
В табличных информационных моделях информация об объекте представляется в виде прямоугольной таблицы, состоящей из столбцов и строк. Представленная в таблице информация наглядна, компактна и легкообозрима.
Таблица типа «объект—свойство» — это таблица, содержащая информацию о свойствах отдельных объектов, принадлежащих одному классу.
Таблица типа «объект—объект» — это таблица, содержащая информацию о некотором одном свойстве пар объектов, чаще всего принадлежащих разным классам.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Какие преимущества обеспечивают табличные информационные модели по сравнению со словесными описаниями? Приведите пример.
3. Приведите примеры табличных информационных моделей, с которыми вы имеете дело:
а) на уроках в школе;
б) в повседневной жизни.
4. К какому типу относится таблица «Табель успеваемости», расположенная в конце вашего дневника?
5. Узнайте, в каких случаях в ячейку таблицы ставится знак х. Почему мы использовали этот знак в таблице (пример 2)?
6. Два игрока играют в следующую игру. Перед ними лежат две кучи камней, в первой из которых 1 камень, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 17. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
7. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость перевозок между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Стоимость перевозок по маршруту складывается из стоимостей перевозок между соседними станциями. Перевозки между населёнными пунктами А, В, С, В, Е осуществляют три компании, представившие стоимость своих услуг в табличной форме. Какая компания обеспечивает минимальную стоимость перевозок из А в В?
8. Соревнования по плаванию были в самом разгаре, когда стало ясно, что первые четыре места займут мальчики из пятёрки лидеров. Их имена: Валерий, Николай, Михаил, Игорь, Эдуард, фамилии: Симаков, Чигрин, Зимин, Копылов, Блинов (имена и фамилии названы в произвольном порядке). Нашлись знатоки, которые предсказали, что первое место займёт Копылов, второе — Валерий, третье — Чигрин, четвёртое — Эдуард. Но ни один из ребят не занял того места, какое ему предсказывали. На самом деле первое место завоевал Михаил, второе — Симаков, третье — Николай, четвёртое — Блинов, а Чигрин не попал в четвёрку сильнейших. Назовите имя и фамилию каждого из лидеров.
9. В Норильске, Москве, Ростове и Пятигорске живут четыре супружеские пары (в каждом городе — одна пара). Имена этих супругов: Антон, Борис, Давид, Григорий, Ольга, Мария, Светлана, Екатерина. Антон живёт в Норильске, Борис и Ольга — супруги, Григорий и Светлана не живут в одном городе, Мария живёт в Москве, Светлана — в Ростове. В каком городе живёт каждая из супружеских пар?
10. Постройте граф, отражающий разновидности информационных моделей.
Электронное приложение к уроку
 |  |  |
| Файлы | Материалы урока | Ресурсы ЭОР |
Cкачать материалы урока