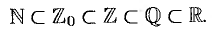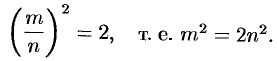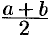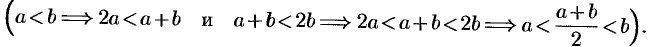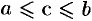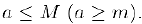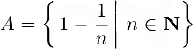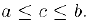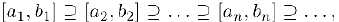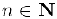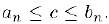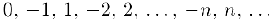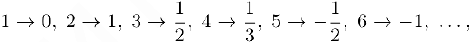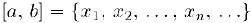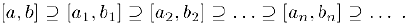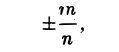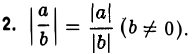к какому числовому множеству не относится число 0
Числовые множества — определения
Числовые множества — введение
Словосочетание «числовые множества» довольно часто встречается в учебниках математики. Там очень часто можно встретить фразы такого плана:
«Бла-бла-бла, где 
Частенько вместо окончания фразы можно увидеть вот такую запись 

Числовых множеств не так уж и много. Ниже можно увидеть определения различных числовых множеств.
Множество натуральных чисел
Множество натуральных чисел включает в себя все целые числа больше нуля — положительные целые числа.
Например: 1, 3, 20, 3057. Множество не включает в себя цифру 0.
Множество целых чисел
В это числовое множество входят все целые числа больше и меньше нуля, а так же ноль.
Множество рациональных чисел
Рациональные числа, вообще говоря, представляют собой множество дробей, которые не сокращаются (если дробь сокращается, то это уже будет целое число, и для этого случая не стоит вводить еще одно числовое множество).
Пример чисел входящих в рациональное множество: 3/5, 9/7, 1/2.
Множество вещественных чисел

где 

Такие числа невозможно представить в виде дроби. В противном случае, подобное число можно было бы отнести к множеству рациональных чисел.
Примеры вещественных чисел:
Давайте рассмотрим значение корня из двух внимательнее. В целочисленной части представлена только одна цифра — 1, поэтому мы можем записать:
В дробной части (после точки) последовательно идут числа 4, 1, 4, 2 и так далее. Поэтому для первых четырех цифр можно записать:

Смею надеяться, что теперь запись определения множества вещественных чисел стала понятней.
Заключение
Следует помнить, что одна и та же функция может проявлять совершенно разные свойства в зависимости от того к какому множеству будет принадлежать переменная. Так что помните основы – они вам пригодятся.
Числовые множества
ЕГЭ по математике — экзамен чисто практический. Однако знания о том, какие бывают числа, необходимы при решении многих задач.
Натуральные числа — это числа, применяемые для счёта предметов. Натуральные числа можно использовать в качестве номеров.
Наименьшее натуральное число — единица¹. Числа 21, 249, 30988 являются натуральными. Все вместе они составляют множество натуральных чисел, обозначаемое буквой N:
Что же такое множество? Это одно из первичных понятий математики, т. е. таких, которые лежат в основе логической системы и уже не определяются через другие понятия. Интуитивно мы понимаем, что множество — это набор или совокупность элементов, объединенных каким-либо общим признаком.
Множества обычно обозначаются заглавными буквами. Множество натуральных чисел мы можем условно изобразить вот так:
Но числа бывают не только натуральными. Индийцы изобрели число ноль и отрицательные числа. Теперь они для нас привычны, но когда-то европейцы — древние греки и римляне — долгое время обходились без нуля. Сейчас нам трудно это представить.
Натуральные числа, целые отрицательные числа и ноль вместе составляют множество целых чисел, которое обозначается Z :
Например, получая в тригонометрическом уравнении серию решений, мы пишем: n ∈ Z, и это означает, что n — целое число.
Очевидно, множество целых чисел включает в себя множество натуральных:
Кроме целых чисел, однако, имеются ещё и дроби.
Стало быть, целые числа — частный случай дробей.
Долгое время — в античности — считалось, что любое число можно записать в виде дроби с числителем и знаменателем. Дело в том, что для древних греков числа и их соотношения были почти священны. Пифагорейцы говорили: «Числа правят миром». Они верили, что все основные принципы мироздания можно выразить языком математики, что соотношения чисел выражают гармонию, закон и порядок природы, перед которым склоняют голову даже олимпийские боги. Греческое искусство, особенно архитектура, подчинялось правилам, канонам. Греки точно установили, какими должны быть пропорции в архитектуре — например, отношение диаметра колонны к её длине — чтобы здание было гармоничным. И все эти пропорции были отношениями целых чисел.
Ещё раз повторим, в чём разница между рациональными и иррациональными числами.
7 : 11 = 0,636363636363.
Мы видим, что цифры повторяются, то есть дробь является периодической. Таким образом, любое рациональное число можно записать десятичной дробью — конечной или бесконечной периодической.
А вот в числе цифры не заканчиваются, и никакой периодичности их следования не наблюдается. Иррациональные числа — это бесконечные непериодические дроби.
Вместе оба множества — рациональных и иррациональных чисел — образуют множество действительных (или вещественных) чисел, которое обозначается R (от слова real).
Возникает вопрос: это всё? Все ли числа, какие только могут быть, содержатся в множестве действительных чисел? Или за его пределами ещё что-то есть?
Для успешной сдачи ЕГЭ других чисел не нужно. Да и, казалось бы, мы назвали все возможные числа. Но вот какой парадокс: положительные и отрицательные числа симметрично расположены на числовой прямой, верно? И при этом из положительных чисел можно извлечь квадратный корень, а из отрицательных — нельзя! Не существует действительного числа, которое при возведении в квадрат даёт −1.
Оказывается, однако, что существует числовое множество, содержащее в себе множество R и бесконечное множество других чисел, не являющихся действительными. В этом множестве находится мнимая единица i, для которой верно i² = −1. И называется оно множеством комплексных чисел.
Комплексные числа служат естественным языком описания многих физических явлений. Те из вас, кто выбрал инженерную специальность (в особенности связанную с распространением волн, электротехникой и радиофизикой), непременно встретятся с ними. В отличие от действительных («вещественных») чисел, применяемых для описания материального, плотного мира «вещей», комплексные числа оказываются удобным инструментом для построения математических моделей волн и колебаний всевозможной природы.
Ну а будущим физикам наверняка интересно будет узнать, что элементарные частицы живут и взаимодействуют по законам именно комплексных чисел. Наукой, описывающей комплексный микромир, является квантовая физика.
¹ В школьной математике ноль не является натуральным числом. Мы ведь не используем его для счёта предметов. Ну какой здравомыслящий человек скажет: «На столе стоит ноль чашек»? 🙂
Пособие для обучающихся «Числовые множества»
Ищем педагогов в команду «Инфоурок»
Государственное образовательное учреждение
среднего профессионального образования
«Алексинский машиностроительный техникум»
Понятие числа возникло в глубокой древности из практической потребности людей и развивалось в процессе развития человечества. Область человеческой деятельности расширялась и соответственно, возрастала потребность в количественном описании и исследовании. Сначала понятие числа определялось теми потребностями счёта и измерения, которые возникали в практической деятельности человека, всё более усложняясь. Позже число становится основным понятием математики, и потребности этой науки определяют дальнейшее развитие этого понятия.
Множества, элементами которых являются числа, называются числовыми.
Примерами числовых множеств являются:
Q=
R—множество действительных чисел.
Между этими множествами существует соотношение
Порядок арифметических действий: сначала выполняются действия в скобках; внутри любых скобок сначала выполняют умножение и деление, а потом сложение и вычитание.
Если число имеет только два делителя (само число и единица), то оно называется простым : если число имеет более двух делителей, то оно называется составным.
Для любых заданных натуральных чисел a и b можно найти наибольший общий делитель. Он обозначается D(a,b). Если числа a и b таковы, что D(a,b) = 1, то числа a и b называются взаимно простыми.
Для любых заданных натуральных чисел a и b можно найти наименьшее общее кратное. Оно обозначается K(a,b). Любое общее кратное чисел a и b делится на K(a,b).
Каждое рациональное число представимо в виде конечной или бесконечной периодической десятичной дроби.
Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.
Основное свойство дроби: если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получится дробь, равная данной.
Если числитель и знаменатель дроби взаимно простые числа, то дробь называется несократимой .
Значимыми цифрами числа называются все его цифры, кроме нулей, стоящих в начале.
Числа не являющиеся целыми или дробными называются иррациональными .
Каждое иррациональное число представляется в виде непереодической бесконечной десятичной дробью.
Множество всех конечных и бесконечных десятичных дробей называется множеством действительных чисел : рациональных и иррациональных.
Множество R действительных чисел обладает следующими свойствами.
1. Оно упорядоченное: для любых двух различных чисел α и b имеет место одно из двух соотношений а
2. Множество R плотное: между любыми двумя различными числами a и b содержится бесконечное множество действительных чисел х, т. е. чисел, удовлетворяющих неравенству a
(a 2a а +b а +b 2 а а
Действительные числа можно изображать в виде точек на числовой прямой. Чтобы задать числовую прямую необходимо отметить на прямой точку, которой будет соответствовать число 0- начало отсчёта, а затем выбрать единичный отрезок и указать положительное направление.
Комплексные числа подразделяются на алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим.
Более общими (но всё ещё счётными) классами чисел, чем алгебраические, являются периоды, вычислимые и арифметические числа (где каждый последующий класс шире, чем предыдущий).
Также надо понимать, что одно выделяемое числовое множество может являться подмножеством другого. Так, например, множество натуральных чисел (N) является подмножеством целых (Z).
С другой стороны, могут быть два числовых множества, по отношению к которым нельзя сказать, что одно является подмножеством другого. Например, в таких отношениях находятся множества положительных (R + ) и отрицательных (R — ) действительных чисел. Они принадлежат неперекрывающимся числовым диапазонам.
Ниже представлена иерархия чисел, для множеств которых справедливо выражение 
Обозначение, запись и изображение числовых множеств
Из большого количества разнообразных множеств особо интересными и важными являются числовые множества, т.е. те множества, элементами которых служат числа. Очевидно, что для работы с числовыми множествами необходимо иметь навык записи их, а также изображения их на координатной прямой.
Запись числовых множеств
N – множество всех натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; J – множество иррациональных чисел; R – множество действительных чисел; C – множество комплексных чисел.
Напомним также следующие обозначения:
Рассмотрим теперь схему описания числовых множеств на примере основных стандартных случаев, наиболее часто используемых на практике.
Таким же образом, объединяя различные числовые промежутки и множества отдельных чисел, возможно дать описание любому числовому множеству, состоящему из действительных чисел. На основе сказанного становится понятно, для чего вводятся различные виды числовых промежутков, такие как интервал, полуинтервал, отрезок, открытый числовой луч и числовой луч. Все эти виды промежутков совместно с обозначениями множеств отдельных чисел дают возможность через их объединение описать любое числовое множество.
Изображение числовых множеств на координатной прямой
В практических примерах удобно использовать геометрическое толкование числовых множеств – их изображение на координатной прямой. К примеру, такой способ поможет при решении неравенств, в которых нужно учесть ОДЗ – когда нужно отобразить числовые множества, чтобы определить их объединение и/или пересечение.
Зачастую и не указывают начало отсчета и единичный отрезок:
В большинстве случаев возможно не соблюдать абсолютную точность чертежа: вполне достаточно схематичного изображения без соблюдения масштаба, но с сохранением взаимного расположения точек относительно друг друга, т.е. любая точка с бОльшей координатой должна быть правее точки с меньшей. С учётом сказанного уже имеющийся чертеж может выглядеть так:
Отдельно из возможных числовых множеств выделяют числовые промежутки интервалы, полуинтервалы, лучи и пр.)
Информация, приведенная в данной статье, призвана помочь получить навык видеть запись и изображение числовых множеств так же легко, как и отдельных числовых промежутков. В идеале записанное числовое множество сразу должно представляться в виде геометрического образа на координатной прямой. И наоборот: по изображению должно с легкостью формироваться соответствующее числовое множество через объединение числовых промежутков и множеств, являющихся отдельными числами.
Числовые множества с примерами решения и образцами выполнения
Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:
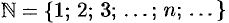
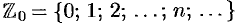
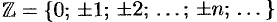
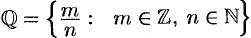
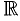
Между этими множествами существует соотношение
Множество 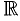
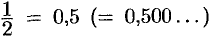
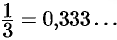
Действительные числа, не являющиеся рациональными, называются иррациональными.
Теорема:
Не существует рационального числа, квадрат которого равен числу 2.
Допустим, что существует рациональное число, представленное несократимой дробью 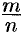
Отсюда следует, что 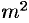
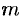
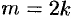
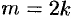
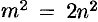
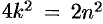
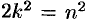
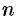
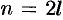
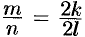
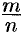
Иррациональное число выражается бесконечной непериодической дробью. Так, 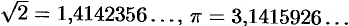
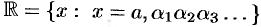
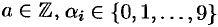
Множество 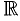
1. Оно упорядоченное: для любых двух различных чисел 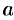
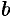
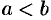
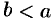
2. Множество 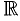
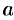
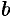
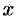
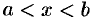
Так, если 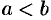
3. Множество 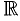
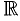
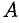
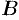
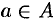
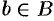
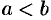
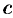
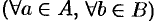
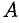
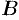
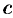
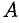
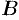
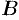
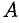
Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек прямой. Это означает, что каждому числу 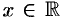
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
Числовые множества
Множество 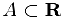
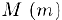
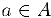
Числа 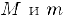
Ограниченное снизу и сверху множество, называется ограниченным.
Наименьшая из мажорант (наибольшая из минорант) называется верхней (нижней) гранью множества А. Верхняя грань обозначается через 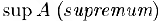
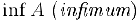
В качестве примера рассмотрим множество
Здесь 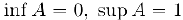
Докажем теперь теорему о существовании граней множества.
Теорема:
Ограниченное сверху (снизу) множество имеет. верхнюю (нижнюю) грань.
Доказательство:
Предположим, для определенности, что множество А ограничено сверху. Обозначим через В множество его мажорант. Тогда для любых чисел 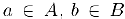
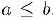
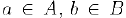
Таким образом, с одной стороны, число с: является мажорантой, а, с другой стороны, оно нс превосходит любой из мажорант и, следовательно, 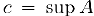
Рассмотрим систему вложенных отрезков
Принцип вложенных отрезков. Любая система вложенных отрезков имеет непустое пересечение.
Доказательство. Пусть множества А и В состоят из левых и правых концов отрезков, соответственно. Так как для любых 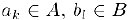
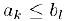
то по свойству полноты множества действительных чисел найдется разделитель 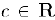
Таким образом, число с принадлежит всех отрезкам системы. Принцип доказан.
Множества можно сравнивать по количеству элементов, содержащихся в них. Конечные множества считаются равномощными, если они имеют одинаковое ’тело элементов. Если множество содержит бесконечное количество элементов, то можно попытаться сравнить его с другим бесконечным множеством простой структуры. например, с множеством натуральных чисел.
Бесконе’шое множество называется счетным, если его элементы можно пронумеровать, т. с. каждый элемент множества получает свой, отличный от других номер, выражающийся натуральным числом.
Примерами счетных множеств могут служить, например, множества целых и рациональных чисел. Целые числа можно пересчитать, расположив их в ряд:
Для того, чтобы пронумеровать рациональные числа, расположим их в следующей бесконечной матрице:
В строках этой матрицы записаны все несократимые рациональные дроби с фиксированным знаменателем. Ясно, что каждому рациональному числу однозначно найдется место в этой матрице. Занумеруем теперь числа матрицы по диагоналям, на’шная с левого верхнего угла, т. е.
где запись 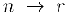
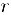
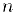
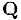
На этих примерах мы наблюдаем любопыппдй парадокс, который является особенностью бесконечных множеств: бесконечное множество может быть равномощно своей части, т. с. содержать столько же элементов, сколько их имеется в собственном подмножестве.
В заключение этого параграфа покажем что существуют множества, которые являются более мощными, чем счетные.
Теорема:
Любой отрезок множества действительных чисел является несчетным множеством.
Доказательство:
Предположим, наоборот, что отрезок 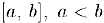
— пронумерованное множество чисел этого отрезка. Выберем внутри данного отрезка отрезок 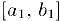
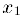
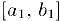
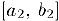
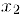
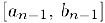
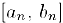
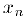
В соответствии с принципом вложенных отрезков, найдется число с, общее для всех отрезков. Пусть 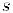
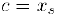
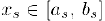
Числовые множества и числовые последовательности
Множества
Понятие м ножества принадлежит к числу первичных, неопределяемых понятий. Употребляя термин «множество», будем понимать под этим любое собрание (совокупность) определенных и различимых между собой элементов, мыслимое как единое целое. Например, мы можем говорить о множестве букв на данной странице, о множестве песчинок на морском берегу, о множестве всех корней уравнения, о множестве всех четных чисел и т. д.
Если А — произвольное множество элементов, то утверждение «элемент о принадлежит множеству А символически записывается так: a ∈ А. Запись a ∈ А (или a∉А) означает, что элемент о не принадлежит множеству А. Если каждый элемент из множества А входит и в множество В, то мы называем А подмножеством множества В и пишем А ⊂ В. Так, множество всех четных чисел Z’ является подмножеством множества Z всех целых чисел. Заметим, что всегда А ⊂ А.
Если А ⊂ В и В ⊂ А, т.е. если каждый элемент множества А есть также и элемент В и наоборот, то мы говорим, что множества А и В равны и пишем А = В. Тем самым множество однозначно определено своими элементами. Пользуясь этим, мы будем иногда обозначать множество его элементами, заключенными в фигурные скобки. Так
суть множества, соответственно состоящие из одного элемента а, двух элементов a и b, трех элементов а, b и с. Часто все элементы множества выписать затруднительно, или невозможно. В таких случаях невыписанные элементы будем заменять точками:
есть множество, состоящее из элементов а, b, с и, может быть, еше некоторых других. Какие эти другие элементы, обозначенные точками, должно быть указано, например:
множество натуральных чисел <1, 2, 3…..п,… >;
множество квадратов натуральных чисел <1, 4, 9,…, п2,… >; множество простых чисел <2, 3,5,7,… >.
Если А ⊂ В, но А ≠ В, то А называют правильной частью множества В (истинным подмножеством множества В).
Иногда мы не знаем заранее, содержит ли некоторое множество хотя бы один элемент. Поэтому целесообразно ввести понятие пустого множества, т. е. множества, не содержащего ни одного элемента. Будем обозначать пустое множество символом ∅. Любое множество содержит пустое множество в качестве подмножества.
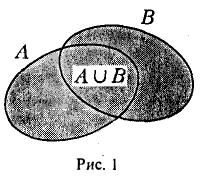
Пусть А и В — два множества. Их суммой или объединением С = A ∪ В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств A и В (рис. 1).
Назовем пересечением множеств А и В множество С = А ∩ В, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В (рис. 2). Например, если А = <1, 2, 3>, В = <2, 3, 4, 5>, то A U В = <1,2, 3, 4, 5>, A ∩ В = <2,3>.
Аналогично определяются объединение и пересечение любого числа множеств.
Если А ∩ В = ∅, то говорят, что множества А и В не пересекаются.
Множество называется конечным, если оно состоит из некоторого натурального числа элементов. Например, конечным является множество всехжителейданного города, а также множество всех людей, населяющих планету Земля. Непустое множество называется бесконечным, если оно не является конечным. Так, множество N = <1, 2,… >всех натуральных чисел является бесконечным множеством.
Пусть А и В — некоторые множества. Говорят, что между множествами А и В установлено взаимнооднозначное соответствие, если каждому элементу множества А поставлен в соответствие один элемент множества В так, что: 1) разным элементам множества А поставлены в соответствие разные элементы множества В и 2) каждый элемент множества В поставлен в соответствие некоторому элементу множества А. Если между двумя конечными множествами А и В удалось установить взаимнооднозначное соответствие, то множество А и В имеют одинаковое число элементов. Множества А и В, между которыми можно установить взаимнооднозначное соответствие, называются эквивалентными.
Обозначение: А
Бесконечное множество А называется счетным, если можно установить взаимнооднозначное соответствие между множеством А и множеством N натуральных чисел, т. е. если А
N. Каждое бесконечное множество содержит счетное подмножество.
Действительные числа. Абсолютная величина
Числа 1, 2, 3,…, п, п + 1,… называются натуральными числами. Дроби вида
где т и п — натуральные числа, а также число 0 называются рациональными числами. В частности, рациональным будет каждое натуральное и каждое целое отрицательное число. Любое рациональное число выражается либо конечной, либо бесконечной периодической десятичной дробью.
Кроме рациональных чисел существуют еще иррациональные числа, которые выражаются бесконечными непериодическими десятичными дробями. Например,
Рациональные и иррациональные числа называются действительными (вещественными) числами.
Можно показать, что множество всех рациональных чисел счетно. Множество всех действительных чисел счетным не является.
Мы будем предполагать, что основные свойства действительных чисел и арифметические действия над ними известны из школьного курса математики.
Определение:
Если а > 0, то отношение |х| ≤ а эквивалентно отношению
-а ≤ х ≤ а (проверьте это!).
Для абсолютных величин верны следующие соотношения:
1. |а • b| = |а| • |b|;
Справедливость этих соотношений вытекает из правила умножения и деления действительных чисел и из определения абсолютной величины.