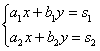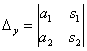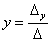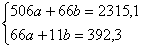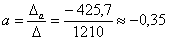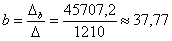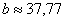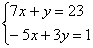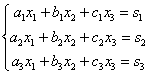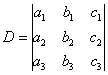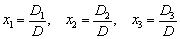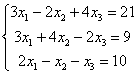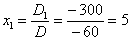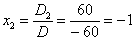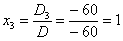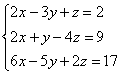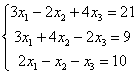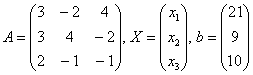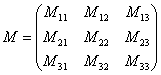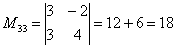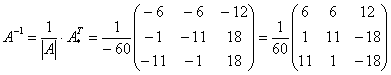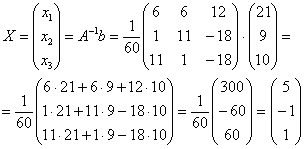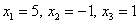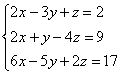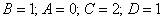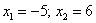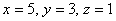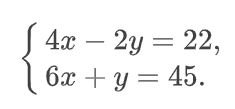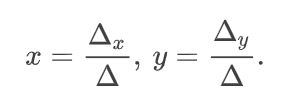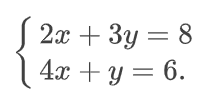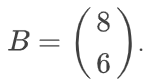к каким слау применим метод обратной матрицы и метод крамера сопоставление
Правило Крамера. Метод обратной матрицы
Представляю Вашему вниманию вторую часть урока Как решить систему линейных уравнений? В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Настоятельно рекомендую скачать программу для автоматизированного решения систем по формулам Крамера и с помощью обратной матрицы. Всегда приятно знать правильный ответ заранее, более того, программа позволит сразу обнаружить ошибку по ходу решения задачи, что значительно сэкономит время!
Решение системы по формулам Крамера
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель 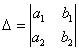
Если 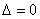
Если 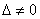
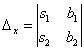
На практике вышеуказанные определители также могут обозначаться латинской буквой 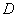
Корни уравнения находим по формулам: 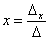
Решить систему линейных уравнений
Решение: Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
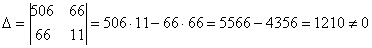
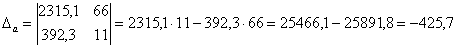
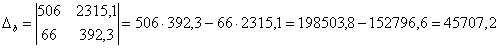
Ответ: 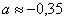
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «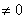
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения 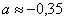
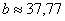
Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если 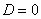
Если 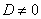
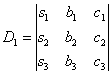
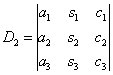
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов 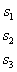
Решить систему по формулам Крамера.
Решение: Решим систему по формулам Крамера. 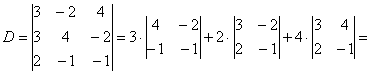
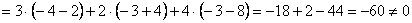
Ответ: 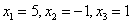
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: 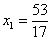
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде 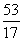
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например: 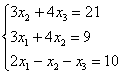
Здесь в первом уравнении отсутствует переменная 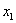
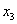
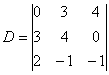
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Решить систему с матричным методом
Решение: Запишем систему в матричной форме: 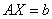
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице 
Решение системы найдем по формуле 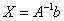
Согласно формуле нам нужно найти обратную матрицу 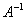
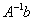
Обратную матрицу найдем по формуле: 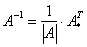
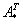
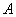
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если 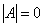
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент: 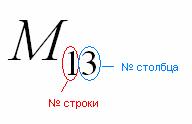
То есть, двойной подстрочный индекс указывает, что элемент 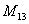
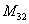
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
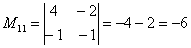
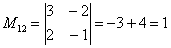
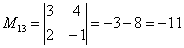
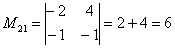
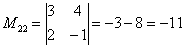
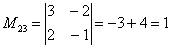
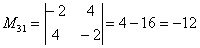
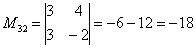
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).
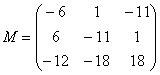
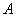
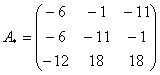
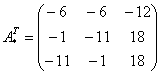
Повторюсь, выполненные шаги мы подробно разбирали на уроке Как найти обратную матрицу?
Теперь записываем обратную матрицу:
Ни в коем случае не вносим 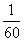
Осталось провести матричное умножение. Умножать матрицы можно научиться на уроке Действия с матрицами. Кстати, там разобран точно такой же пример.
Обратите внимание, что деление на 60 выполняется в последнюю очередь.
Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже рассказал, когда мы разбирали правило Крамера.
Ответ:
Решить систему с помощью обратной матрицы.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Наиболее универсальным способом решения системы является метод исключения неизвестных (метод Гаусса). Доступно объяснить алгоритм не так-то просто, но я старался!.
Пример 3:
Пример 6:
Пример 8: 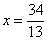
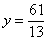
Примеры 10, 12:
Автор: Емелин Александр
(Переход на главную страницу)

Разбираемся в решении линейных уравнениях раз и навсегда
Одной из наиболее важных тем курса алгебры является решение систем линейных уравнений. Давайте узнаем, как научиться с ними расправляться разными методами.
Системой линейных алгебраических уравнений (СЛАУ) называется объединение n линейных уравнений, каждое из которых содержит k переменных:
Отметим, что не всегда количество неизвестных будет совпадать с количеством уравнений в системе, но системы такого уровня рассматриваются в старшей школе. В данной статье речь пойдёт о системах двух уравнений с двумя переменными, за исключением пункта «Решение систем линейных уравнений методом Гаусса», где мы рассмотрим систему с тремя переменными. Вот несколько методов решения систем линейных уравнений.
Решение системы линейных уравнений методом подстановки («школьный метод»)
Метод подстановки знаком из курса школьной математики, его изучают в 7 классе. Это самый лёгкий способ решения систем линейных уравнений. Его алгоритм достаточно прост и заключается в следующем:
Для примера применим данный метод решения к следующей системе уравнений:
Согласно первому пункту алгоритма решения СЛАУ нужно выразить одну переменную через другую. В данном случае удобно из второго уравнения системы выразить переменную y через переменную x:
Далее подставим переменную y, выраженную через x, в первое уравнение системы. Получим:
Тогда можно записать систему уравнений, равносильную первой:
Раскроем скобки и приведём первое уравнение системы к следующему виду:
Теперь найдём значение y, подставив значение переменной x в выражение для второй переменной:
Применив данный метод к рассматриваемой системе линейных уравнений, мы нашли пару чисел (7;3), являющуюся её решением.
Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда». Выберите класс и получите неделю бесплатного доступа к курсу алгебры по промокоду ALGEBRA2021: 7 класс, 8 класс, 9 класс, 10 класс.
Решение системы линейных уравнений методом почленного сложения (вычитания) уравнений системы
Суть данного метода состоит в избавлении от одной из переменных в системе уравнений, алгоритм метода достаточно простой:
В качестве примера решим систему уравнений:
методом почленного сложения (вычитания). Здесь будет достаточно просто «избавиться» от переменной y. Для этого почленно умножим обе части первого уравнения системы на 2:
получим равносильную систему уравнений:
Теперь прибавим к левой части первого уравнения левую часть второго уравнения, а к правой части первого уравнения — правую часть второго. В итоге получим уравнение вида:
Решим это уравнение относительно единственной переменной:
Подставим найденное значение в первое уравнение исходной системы и найдём значение y:
Итак, пара чисел (4;3) является решением системы линейных уравнений с двумя переменными. Данное решение было получено методом сложения.
Решение системы линейных уравнений по формулам Крамера
Чтобы решить систему линейных уравнений методом Крамера, нужно познакомиться с понятием определителя.
Определение
Определителем системы называют запись чисел в квадратной таблице, в соответствие которой ставится число по некоторому правилу.
Давайте познакомимся с этим правилом. Пусть даны четыре числа a, b, c, d. Пусть они имеют следующее расположение в квадратной таблице:
Значение определителя системы в этом случае находится по формуле:
Определитель, составленный из коэффициентов при переменных в линейной системе уравнений, называется главным определителем системы. Будем обозначать его Δ. Например, у рассмотренной выше системы уравнений:
главный определитель будет иметь вид:
Найдём его значение:
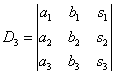
Для решения системы линейных уравнений методом Крамера нам понадобятся ещё два определителя, которые называются вспомогательными:
Отметим, что в данные определители уже входят правые части каждого уравнения системы. Так, в определитель Δₓ первым столбцом записываем правые части уравнений (так называемые свободные члены уравнений), второй столбец оставляем таким же, как в главном определителе системы. В определитель Δу вторым столбцом записываем правые части уравнений, а первый столбец оставляем таким же, как в главном определителе системы.
Итак, формулы Крамера для решения системы двух линейных уравнений с двумя переменными:
Отметим, что данный метод решения СЛАУ можно применять лишь в тех случаях, когда Δ ≠ 0.
Убедимся в том, что данные формулы работают, подставив в них ранее найденные значения определителей:
Пара чисел (4;3) действительно является решением данной системы уравнений.
Обобщим алгоритм нахождения решений системы двух линейных уравнений с двумя переменными методом Крамера. Пусть дана система линейных уравнений:
Решение системы линейных уравнений с помощью обратной матрицы
Матрицей системы линейных уравнений называется таблица, составленная из коэффициентов при переменных. Так, для системы вида:
матрицей A является:
Столбцом свободных коэффициентов будем называть
а столбцом переменных —
Тогда систему уравнений можно переписать в виде:
Поясним, как происходит умножение матрицы на столбец. В матрице A есть строки: (а₁₁, а₁₂) и (а₂₁, а₂₂) а также столбцы (а₁₁, а₂₁) и (а₁₂, а₂₂).
При умножении матрицы на столбец X получается столбец, а само умножение происходит по следующему правилу:
Рассмотрим алгоритм поиска обратной матрицы:
1) вычислить определитель матрицы A:
2) записать матрицу миноров M. Для этого нужно просто переставить числа в матрице A следующим образом:
3) записать матрицу алгебраических дополнений А ͙. Для этого необходимо лишь поменять знаки коэффициентов а₁₂ и а₂₁ в матрице миноров M, в результате чего получим:
записать матрицу, транспонированную к матрице алгебраических дополнений:
найти обратную матрицу А⁻¹, разделив каждый элемент матрицы Аᵀ ͙ на значение определителя матрицы A, то есть
Для нахождения неизвестных нужно полученную обратную матрицу А⁻¹ умножить на столбец свободных коэффициентов:
Поясним всё на примере решения системы линейных уравнений с двумя переменными:
столбец свободных коэффициентов:
Следуя алгоритму решения СЛАУ, найдём обратную матрицу А⁻¹:
1) определитель матрицы A равен
3) матрица алгебраических дополнений:
4) матрица, транспонированная к матрице алгебраических дополнений:
5) обратная матрица:
Теперь умножим найденную обратную матрицу на столбец свободных коэффициентов:
Пара чисел (1;2) является решением данной системы уравнений.
Решение системы линейных уравнений методом Гаусса
Этот метод позволяет достаточно легко находить решения систем линейных уравнений, в которых более двух уравнений и неизвестных. По сути, этот метод является обобщением метода подстановки. Итак, как можно решить систему линейных уравнений? Рассмотрим этот способ на примере системы трёх уравнений с тремя неизвестными.
На первом этапе решения систему уравнений необходимо привести к трапециевидной форме, которая выглядит следующим образом:
Для этого нужно провести несложные линейные преобразования с коэффициентами расширенной матрицы системы. Расширенная матрица системы отличается от матрицы системы лишь тем, что она содержит ещё и столбец правых частей уравнений, который записывается справа. Преобразования включают в себя сложение или вычитание строк матрицы, а также умножение элементов строки на число.
Применим данный метод к системе линейных уравнений с тремя переменными:
Расширенная матрица A данной системы принимает вид:
Проводя преобразования строк, нужно добиться того, чтобы в третьей строке расширенной матрицы на первом и втором местах были нули, а во второй строке — нуль на первом месте (возможно, при этом во второй строке будет ещё нуль и на третьем месте).
Вначале вычтем из второй строки матрицы первую строку, умноженную на два, в результате во второй строке окажется два нуля. Затем вычтем из третьей строки первую строку, умноженную на три, в результате чего в третьей строке окажется только один ноль:
С одной стороны, можно остановиться на данном этапе, поменять вторую и третью строку местами, решить систему уравнений, соответствующую полученной расширенной матрице:
С другой стороны, следуя алгоритму решения системы уравнений, необходимо вычесть из третьей строки расширенной матрицы вторую строку и получить два нуля в последней строке матрицы:
Это позволит перейти к решению ещё более простой системы линейных уравнений:
Итак, решение системы линейных уравнений методом Гаусса: x = 1, y = 2, z = 3.
Заключение
В этой статье мы разобрали следующие основные способы решения систем линейных уравнений:
Надеемся, что теперь вы сможете без труда справиться с любым линейным уравнением.
У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Интересное по рубрике
Найдите необходимую статью по тегам
Подпишитесь на нашу рассылку
Мы в инстаграм
Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Рекомендуем прочитать
Реальный опыт семейного обучения
Звонок по России бесплатный
Посмотреть на карте
Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.