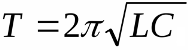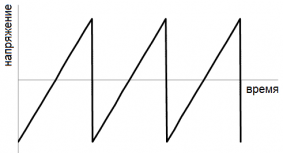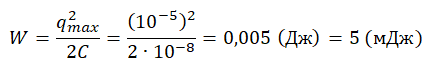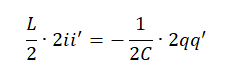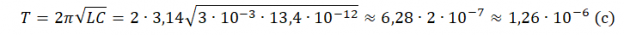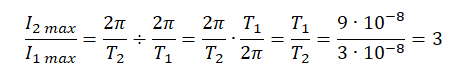Электрические колебания: виды и характеристики, амплитуда, частота и фаза колебаний

Колебания — процессы, многократно повторяющиеся или приблизительно повторяющиеся через некоторые промежутки времени. Колебательные процессы широко распространены в природе и в технике.

В электротехнике и электронике приходится иметь дело с самыми разнообразными типами электрических колебаний, т. е. колебаний напряжений и токов в различных электрических цепях, а также с механическими колебаниями, например колебаниями мембран микрофонов или громкоговорителей.

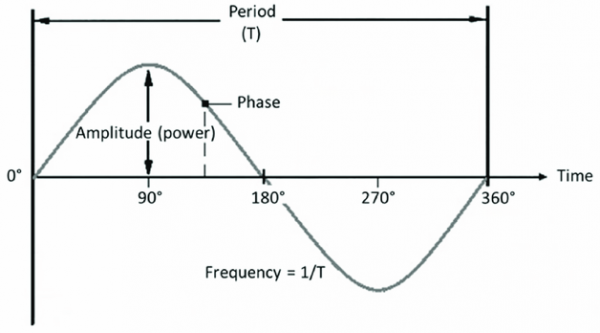
Колебания, как процессы повторяющиеся, характеризуются, во-первых, наибольшими отклонениями, которых достигает колеблющаяся величина, или амплитудой колебаний, во-вторых, частотой, с которой происходят повторения одних и тех же состояний, или частотой колебаний, и, в-третьих, тем, какое именно состояние, какая фаза процесса соответствует моменту начала отсчета времени. Эта последняя характеристика колебательного процесса называется «начальной фазой» или для краткости просто «фазой».

Характеристики колебаний (амплитуда, период, частота и фаза):

В зависимости от того, что происходит с амплитудой, различают колебания:

стационарные или незатухающие, амплитуда которых не меняется со временем ;

затухающие, амплитуда которых уменьшается со временем ;

нарастающие, амплитуда которых нарастает со временем ;

модулированные по амплитуде, амплитуда которых со временем то возрастает, то убывает.

В зависимости от того, как повторяются колебания со временем, различают колебания:

периодические, т. е такие, у которых все состояния повторяются точно через определенные промежутки времени ;

приблизительно периодические, при которых все состояния лишь приблизительно повторяются, например, затухающие или частотно-модулированные (т. е. колебания, частота которых все время изменяется в некоторых пределах около какого-то определенного значения).

синусоидальные (гармонические) или близкие к синусоидальным ;

релаксационные, форма которых существенно отличается от синусоидальных.

Наконец, по происхождению колебательного процесса различают:

собственные или свободные колебания, возникающие в результате происшедшего в системе толчка (или вообще нарушения равновесия системы) ;

вынужденные возникающие в результате длительного внешнего колебательного воздействия на систему, и автоколебания, происходящие в системе при отсутствии внешних воздействий, в силу способности самой системы поддерживать колебательный процесс в ней.

Быстрые же колебания создаются при помощи специальных методов, среди которых в современной технике наибольшую роль играют электронные генераторы.

В зависимости от частоты принято делить электрические колебания на две группы — низкой частоты, частота которых ниже 15 000 гц, и высокой частоты, частота которых больше 15 000 гц. Граница эта выбрана потому, что колебания ниже 15 000 гц производят ощущение звука в человеческом ухе, колебаний же с частотой выше 15 000 гц человеческое ухо не слышит.

Частота собственных колебаний в контуре приближенно определяется т. н. формулой Томсона:

Т. к. всякий контур обладает сопротивлением, в котором происходят потери энергии и выделяется тепло, то собственные колебания в контуре всегда будут затухающими. Иначе говоря, колебательный контур возвращается к электрическому «равновесию» в результате затухающего колебательного процесса.

Если сопротивление контура очень велико, то он представляет собой апериодический контур, в котором собственные колебания не возникают. Созданные в таком контуре начальные напряжения и токи затухают, не испытывая колебаний, а монотонно. Иначе говоря, такой контур при нарушении электрического «равновесия» апериодически (т. е. без колебаний) возвращается к положению «равновесия».

Источник

Электромагнитные колебания

теория по физике 🧲 колебания и волны

Заставить колебаться можно любую материю. Так, колебаться могут не только физические тела, состоящие из вещества, но и электромагнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными частицами. Когда происходят колебания в механической системе, говорят, что тело совершает периодически повторяющиеся движения — оно отклоняется от положения равновесия то в одну, то в другую сторону. Когда происходят электромагнитные колебания, говорят, что электромагнитное поле периодически изменяется во времени, то есть его характеристики, то уменьшаются, то увеличиваются относительного некоторого среднего значения, которое является для них «положением равновесия».

Электромагнитные колебания — периодическое изменение во времени напряженности и индукции электромагнитного поля.

Напомним, что напряженность E представляет собой количественную характеристику электромагнитного поля, а индукция B — силовую. Причем электромагнитное поле — это взаимосвязанные между собой электрическое и магнитные поля. Так, проводник с током создает вокруг себя магнитное поле. Оно тем сильнее, чем выше сила тока в этом проводнике, которая напрямую зависит от напряжения в нем (или количества заряда, прошедшего через него за единицу времени). Поэтому изменения напряжения и силы тока в проводнике вызывают изменения напряженности и индукции магнитного поля. Следовательно, можно сделать вывод, что:

Электромагнитные колебания — периодические или почти периодические изменения во времени заряда, силы тока или напряжения.

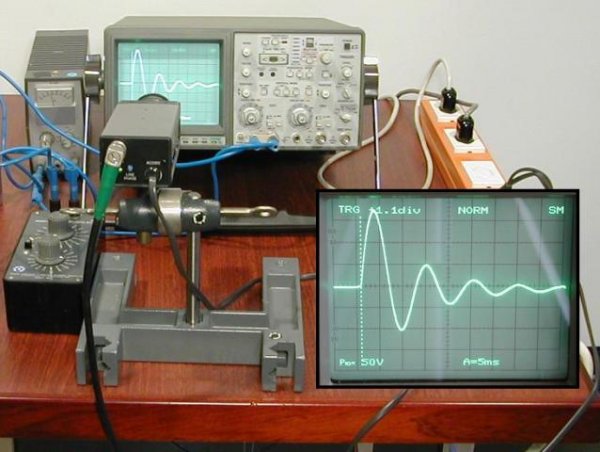
Осциллограф

Но если колебания физических тел наблюдать легко, то колебания электромагнитного поля обнаружить без специальных приборов нельзя. Ведь увидеть изменения заряда, силы тока или напряжения невозможно. Использовать для этого электроизмерительные приборы (гальванометры, вольтметры или амперметры) тоже неудобно, поскольку электромагнитные колебания происходят с гораздо большей частотой по сравнению с механическими. Поэтому специально для визуализации электромагнитных колебаний был создан прибор, который называется осциллографом.

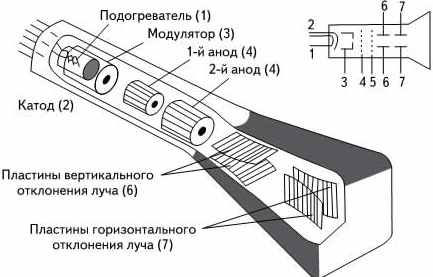
Осциллограф, схему которого вы видите ниже, представляет собой электронно-лучевую трубку. Через нее проходит узкий пучок электронов и попадает на экран, который начинает светиться при бомбардировке электронами.

На горизонтально отклоненные пластины трубки подается переменное напряжение развертки u_p пилообразной формы (см. рисунок ниже). Оно медленно нарастает и быстро падает. Поэтому электрическое поле между пластинами заставляет электронный луч пробегать экран в горизонтальном направлении с постоянной скоростью и затем почти мгновенно возвращаться назад. После этого весь процесс повторяется.

Если же присоединить вертикально отклоняющие пластины трубки к конденсатору, то колебания напряжения при его разрядке вызовут колебания луча в вертикальном направлении. В результате на экране осциллографа образуется временная развертка колебаний. Она напоминает синусоиду или косинусоиду подобно той, с помощью которой можно описать механические колебания.

С течением времени электромагнитные колебания затухают. Такие колебания являются свободными. Напомним, что свободными колебаниями называют такие колебания, которые возникают в колебательной системе после выведения ее из положения равновесия. В нашем случае система выводится из равновесия при сообщении конденсатору заряда. Зарядка конденсатора эквивалента отклонения математического маятника от положения равновесия.

В электрической цепи также можно получить вынужденные колебания, которые будут происходить до тех пор, пока на колебательную систему действует периодическая внешняя сила. Вынужденными электромагнитными колебаниями называют колебания в цепи под действием внешней периодической электродвижущей силы.

Колебательный контур

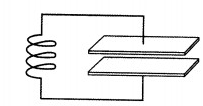
Колебательный контур — простейшая система, к которой могут происходить свободные электромагнитные колебания.

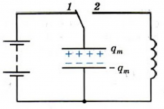
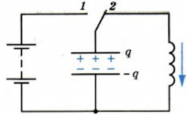
Колебательный контур состоит из конденсатора и катушки, присоединенной к его обкладкам (см. рисунок выше). Попробуем выяснить, почему в этом контуре возникают электромагнитные колебания. Для этого зарядим конденсатор, присоединив его на некоторое время к батарее с помощью переключателя (см. схему ниже).

При этом конденсатор получит энергию, равную:

Теперь переведем переключатель в положение 2 (см. схему ниже). После этого конденсатор начнет разряжаться, и в цепи появится электрический ток. Сила тока достигнет максимального значения не сразу, а будет увеличиваться постепенно. Это объясняется явлением самоиндукции. При появлении тока возникает переменное магнитное поле. Это переменное магнитное поле порождает вихревое электрическое поле в проводнике. Вихревое электрическое поле при возрастании магнитного поля действует против тока и препятствует его мгновенному увеличению.

По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля тока, которая определяется формулой:

где i — сила переменного тока, L — индуктивность катушки.

Полная энергия W электромагнитного контура равна сумме энергий магнитного и электрического полей:

В момент, когда конденсатор полностью разрядится (q = 0), энергия электрического поля станет равной нулю. Но согласно закону сохранения энергии, максимальное значение обретет энергия магнитного поля. Сила тока в этот момент примет максимальное значение I_max.

К этому моменту разность потенциалов на концах катушки становится равной нулю. Но, несмотря на это, электрический ток не может исчезнуть сразу. Этому снова препятствует явление самоиндукции. Как только сила тока и созданное им магнитное поле начнут уменьшаться, возникает вихревое электрическое поле, которое поддерживает ток.

Конденсатор будет перезаряжаться до тех пор, пока сила тока, постепенно уменьшаясь, не станет равной нулю. Энергия магнитного поля в этот момент тоже будет равна нулю, а энергия электрического поля конденсатора опять будет максимальной. После этого конденсатор снова начнет перезаряжаться, и система вернется в исходное состояние.

Из-за частичных потерь энергии электромагнитные колебания являются затухающими. Если бы потерь не было, полная энергия система была бы постоянной и была бы равной:

Пример №1. После того как конденсатору колебательного контура был сообщен заряд q = 10 –5 Кл, в контуре возникли затухающие колебания. Какое количество теплоты выделится в контуре к тому времени, когда колебания в нем полностью затухнут? Емкость конденсатора C = 0,01 мкФ.

Поскольку с каждым колебанием колебательный контур теряет часть энергии в виде выделения тепла, ко времени, когда колебания полностью затухнут, выделится полная электромагнитная энергия системы. Ее можно определить формулой:

Сходство электромагнитных колебаний в контуре со свободными механическими колебаниями

Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями (к примеру, колебаниями тела, закрепленного на пружине). Сходство относится не к природе самих величин, которые периодически изменяются, а к процессам периодического изменения различных величин.

Соответствие между механическими и электрическими величинами при колебательных процессах

Уравнение, описывающее процессы в колебательном контуре

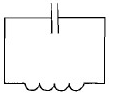
Рассмотрим колебательный контур, сопротивлением R которого можно пренебречь (см. схему ниже).

Полная электромагнитная энергия равна сумме энергий магнитного и электрического полей:

Если его сопротивление равно 0, то полная механическая энергия с течением времени не меняется. А производная константы равна нулю. Следовательно, сумма производных от каждой составляющей этой энергии также равна нулю.

Первая производная по времени характеризует скорость изменения физической величины. Следовательно, эта формула позволяет сделать вывод о том, что скорость изменения энергии магнитного поля равна скорости изменения электрического поля. Знак «минус» указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля уменьшается (и наоборот).

Вычислив обе производные, получим:

Но производная заряда по времени представляет собой силу тока в данный момент времени:

Поэтому мы можем записать уравнение иначе:

Производная силы тока по времени представляет собой вторую производную заряда по времени:

Подставив это равенство в уравнение, и преобразовав его путем деления на величину Li, получим основное уравнение, описывающее свободные электрические колебания в контуре:

Формула Томсона

Следовательно, период свободных колебаний в контуре равен:

Эта формула называется формулой Томсона.

Пример №2. Колебательный контур состоит из катушки индуктивностью L = 0,003 Гн и плоского конденсатора емкостью C = 13,4 пФ. Определите период свободных колебаний в контуре.

13,4 пФ = 13,4∙10 –12 Ф

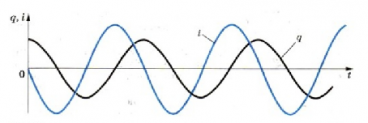
Гармонические колебания заряда и тока

Заряд конденсатора меняется с течением времени подобно тому, как координата при механических колебаниях изменяется со временем по гармоническому закону (в случае, когда в начальный момент времени отклонение от положения равновесия максимально):

где q m a x — амплитуда колебаний заряда.

Сила тока также совершает гармонические колебания:

где I m a x — амплитуда колебаний силы тока, равная произведению циклической частоты на амплитуду колебаний заряда:

I m a x = q m a x ω 0

Пример №3. В двух идеальных колебательных контурах с одинаковой индуктивностью происходят свободные электромагнитные колебания, причём период колебаний в первом контуре 9⋅10 −8 с, во втором 3⋅10 −8 с. Во сколько раз амплитудное значение силы тока во втором контуре больше, чем в первом, если максимальный заряд конденсаторов в обоих случаях одинаков?

Максимальная сила тока равна:

I m a x = q m a x ω 0

Так как максимальный заряд конденсаторов одинаков в обоих контурах, отношение силы тока во тором контуре к силе ток в первом контуре равно:

Циклическую частоту выразим из формулы Томсона:

Автоколебания

Незатухающие вынужденные колебания поддерживаются в цепи действием внешнего периодического напряжения. Но существует способ создания незатухающих колебаний, при котором колебательная система сама регулирует поступление энергии в колебательный контур для компенсации потерь энергии на резисторе.

Автоколебательные системы — системы, в которых генерируются незатухающие колебания за счет поступления энергии от источника тока внутри системы.

Автоколебания — незатухающие колебания, существующие в системе без воздействия на нее внешних периодических сил.

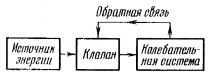
Самый простой пример автоколебательной системы — это генератор на транзисторе. Транзистор представляет собой полупроводниковое устройство, состоящее из эмиттера, базы и коллектора и имеющее 2 p–n перехода. Колебания тока в контуре вызывают колебания напряжения между эмиттером и базой, которые, в свою очередь, управляют силой тока в цепи колебательного контура (обратная связь). От источника напряжения в контур поступает энергия, компенсирующая потери энергии в контуре на транзисторе.

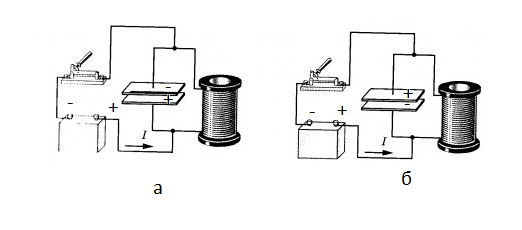
Схема автоколебательной системы представлена ниже.

Преимуществом такой схемы является то, что конденсатор при этом подключается к источнику тока только тогда, когда присоединенная к положительному источнику тока пластина конденсатора заряжена положительно (рис. а). Только в этом случае конденсатор восполняет потери энергии, выделенной на резисторе.

Если бы источник тока был включен всегда, восполнения потерь не происходило бы. Поскольку конденсатор разряжался бы в момент, когда он соединен с источником тока пластиной, заряженной отрицательно (рис. б).

В двух идеальных колебательных контурах происходят незатухающие электромагнитные колебания. Максимальное значение заряда конденсатора во втором контуре равно 6 мкКл. Амплитуда колебаний силы тока в первом контуре в 2 раза меньше, а период его колебаний в 3 раза меньше, чем во втором контуре. Определите максимальное значение заряда конденсатора в первом контуре.

Источник

Каган И.Е. О «фазе» и гармонических колебаниях

Каган И.Е. О «фазе» и гармонических колебаниях // Фiзiка: праблемы выкладання. – 2000. – № 3. – С. 57-60.

При изучении гармонических колебаний учащиеся обязательно сталкиваются с понятием «фаза колебаний». Автор приводит несколько определений этого понятия, объясняет физический смысл данной величины.

При изучении гармонических колебаний учащиеся обязательно сталкиваются с понятием «фаза колебаний». В IX классе это понятие не изучается, а в XI классе – часто очень бегло.

Надо заметить еще, что понять смысл гармонического колебания учащимся лучше всего удается в XI классе, потому что они уже знают основы тригонометрии и умеют дифференцировать простейшие функции.

В некоторых учебниках приводится дифференциальное уравнение второго порядка

(1)

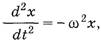
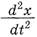
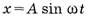
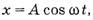
где х – смещение маятника, ω – циклическая частота, – вторая производная смещения по времени, т.е. ускорение. Решениями этого уравнения являются функции или

(2)

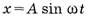
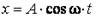
т.е. подчеркивается, что гармоническое колебание является синусоидальным или косинусоидальным. Однако в программе средней школы по математике не предусмотрено решение дифференциальных уравнений второго порядка. Как же быть? Думаю, что лучше всего в этом случае с самого начала использовать функцию или .

Если дважды каждую из них продифференцировать по времени, получим исходное дифференциальное уравнение (1).

Учащиеся IX класса не владеют понятием производной и еще не готовы к этой информации. Вот почему в альтернативной программе по физике для 12-летней средней школы раздел «Колебания и волны» вынесен в X класс. Величина

(3)

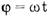
является фазой колебания. Проще всего ее определить с точки зрения математики. В некоторых учебниках математики фазой называют все, что стоит под знаком синуса или косинуса.

Однако у фазы имеется и физический смысл.

Тогда можно сказать о фазе, что это время, выраженное в угловой мере (радианах, градусах), а заодно и в долях периода. Ведь фаза может определять долю периода, прошедшую с момента начала колебания.

Здесь уместно привести пример, показывающий удобство использования понятия «фаза» вместо времени.

Например, никто не сможет сказать, какое смещение будет у маятника в какой-то момент времени, если не известен период колебания. Но всегда можно ответить, какое будет смещение маятника, если известна фаза колебания, не зная, каков по величине период колебания.

Все вышесказанное вполне подходит и для электромагнитных колебаний.

С понятием «фаза» мы сталкиваемся не только в таком упорядоченном периодическом процессе, как колебания. Это понятие применимо к любому процессу и не обязательно к периодическому как определенная часть процесса или определенный момент в развитии того или иного процесса. Все части, на которые разбит тот или иной процесс, можно считать фазами, причем чем мельче раз биение, чем мельче «фазы», тем точнее можно представить ход процесса.

Понятием «фаза» мы пользуемся и в случае «фазовых переходов», т.е. при изменении агрегатного состояния вещества. При этом фаза имеет другой смысл, но и здесь ее можно рассматривать как агрегатное состояние вещества из трех или четырех возможных состояний.

Источник

Фаза колебаний.

Фаза колебаний — это аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс. Для гармонических колебаний:

где φ = ωt + φ₀ — фаза колебания, А — амплитуда, ω — круговая частота, t — время, φ₀ — началь­ная (фиксированная) фаза колебания; в момент времени t = 0φ = φ₀. Фаза выражается в радианах.

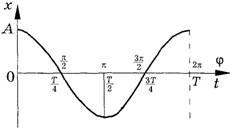
Фаза гармонического колебания при постоянной амплитуде определяет не только координату колеблющегося тела в любой момент времени, но и скорость и ускорение, которые тоже изменяются по гармоническому закону (скорость и ускорение гармонических колебаний — это первая и вторая производные по времени функции (см. рис. ниже), которые, как известно, снова дают синус и косинус). Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние ко­лебательной системы в любой момент времени.

Два колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами. Так как ω = 2π/Т, то

Отношение t/T показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выра­женному в долях периода, соответствует значение фазы, выраженной в радианах.

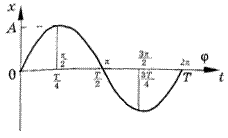
Сплошная кривая на рисунке — это зависимость координаты от времени и одновременно от фа­зы колебаний (верхние и нижние значения на оси абсцисс соответственно) для точки, совершающей гармонические колебания по закону:

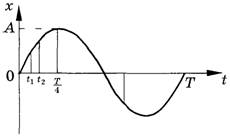
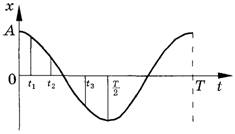
Здесь начальная фаза равна нулю φ₀ = 0. В начальный момент времени амплитуда максимальна. Это соответствует случаю колебаний тела, прикрепленного к пружине (или маятника), которое в начальный момент времени отвели от положения равновесия и отпустили. Описание колебаний, начинающихся из положения равновесия (например, при кратковременном толчке покоящегося шарика), удобнее вести с помощью функции синуса:

Как известно, cos φ = sin (φ + π/2), поэтому колебания, описываемые уравнениями x = x_m cos ω₀ t и x = x_m sin ω₀ t, отличаются друг от друга только фазами. Разность фаз, или сдвиг фаз, составляет π/2. Чтобы определить сдвиг фаз, нужно колеблющуюся величину выразить через одну и ту же три­гонометрическую функцию — косинус или синус. Пунктирная кривая на рисунке выше (это график уравнения x = x_m sin ω₀ t) сдвинута относительно сплошной на π/2.

Источник