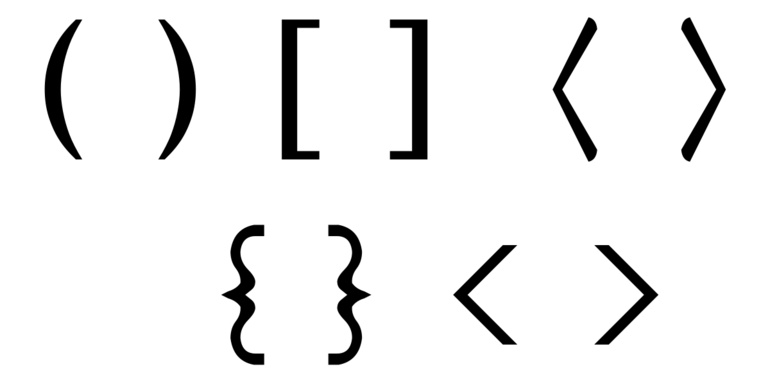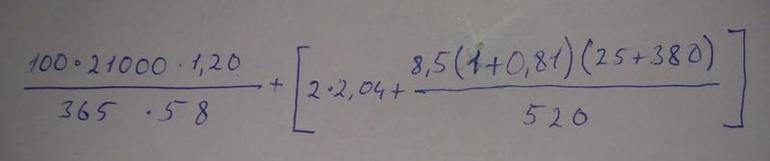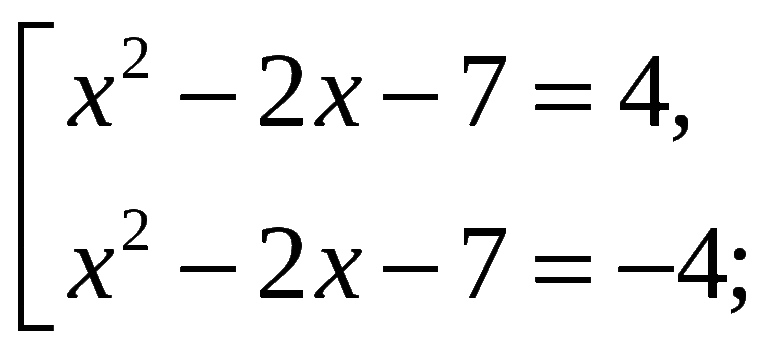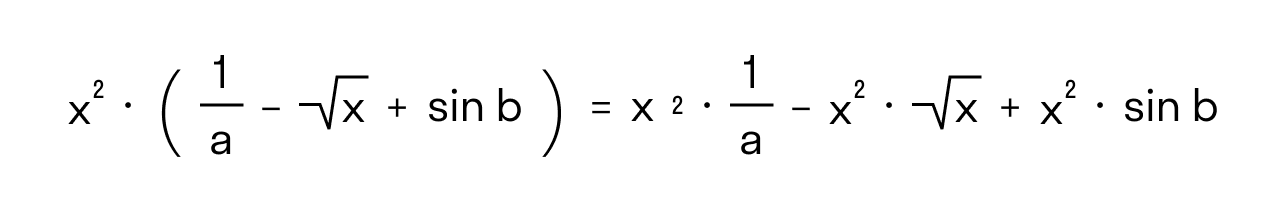что значат разные скобки в алгебре

Скобки в математике

Вы будете перенаправлены на Автор24

Скобки в математике играют очень важную роль: с помощью них задаётся порядок действий с выражением, обозначаются границы промежутков и необходимость выполнения какого-либо действия над выражением. Также с помощью скобок обозначаются вектора и матрицы и действия с множествами.

Использование круглых скобок в математике

Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.

Первое применение.

С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.

В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.

Второе применение.

Третье применение.

Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.

$(x+2)^2; \int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$

Четвёртое применение.

Пятое применение.

Готовые работы на аналогичную тему

Пятое применение.

Квадратные скобки в математике

Что же означают квадратные скобки в математике и для чего они используются?

Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.

Первое применение.

Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.

Второе применение.

Третье применение.

С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.

$\left [ \begin x +32=2y \\ y^2-12=0 \\ \end\right.$

Фигурная скобка в математике

Первое применение.

С помощью символа фигурной скобки обозначают систему уравнений, решением которой являются корни, подходящие для всех уравнений, включённых в систему.

Второе применение.

Третье применение.

Треугольные скобки

Источник

Общая характеристика

Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.

Значение и разновидности

Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.

В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.

Разновидности:

Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.

В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.

Основные цели квадратной скобки в математике:

Другие варианты расчета:

Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.

Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.

Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.

На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.

Одинарные или двойные выражения

Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.

В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.

Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.

По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.

В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.

В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).

Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0

Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.

Прочие знаки

Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.

Удобство записи системы уравнений

Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.

Источник

Как объяснить ребёнку, где и зачем нужны скобки?

Довольно легко объяснить, как раскрывать скобки в математических выражениях: это обязательный раздел в учебниках по математике/алгебре за 6-7 классы, и в интернете куча примеров и руководств.

Сейчас у меня другая проблема: ученик не понимает, зачем и когда нужно ставить скобки. То есть порядок действий расставляет хорошо (хотя из-за невнимательности может ошибиться в сложных случаях). Скобки в уравнениях раскрывает хорошо (хотя надо бы ещё повторить сложные случаи, но это не проблема). Но нет понимания того, какую проблему решают скобки, для чего они нужны, когда их нужно использовать.

Для прошлого занятия я нагенерировал лист словесных выражений вида:

Скобки вокруг отрицательных чисел ставить научились.

Помучались со степенью. Были такие варианты, квадрат числа −3 это:

Оторвали руку от лица и разобрались. Это не так сложно, достаточно один раз заучить, где скобки при степени у отрицательного числа.

Но объяснить то, что скобки «иногда» нужны вокруг действия, которое без них должно выполниться вторым, объяснить не получается. Эти выражения я пытался применить так.

Я: Давай выпишем алгебраическое выражение для первого примера

Он: Да, всё верно, даже скобки стоят

Я: Окей, прочитай то, что получилось

Он: Минус 5 умножить.

Я: Нет, нет, давай по всем правилам

Я: Отлично, вот только с чего мы начинали?

Я: *Тирада про приоритет операций*

Он: Понял! Надо, чтобы сумма шла раньше: (-5) + 2 * 4

Я: Ааааа! *Тирада про скобки*

Он: Ок, добавляю скобки: (-5) + (2 * 4)

И это только начало. Боюсь, что случится, когда дальше по программе будут перемножать дроби вроде:

2x/3 * (x+1)/5 = 2x(x+1) / 15

Тяжело тут это изобразить, но слева роль скобок играет дробь, а справа нужно явно поставить скобки. Обычно тут всё становится понятно после пары примеров, но в этом случае я не знаю, что будет.

Люди добрые, подскажите, что делать!

Edit: Примерно в половине примеров с распечатки ставит скобки не там. То есть всё равно что монетку подбрасывает.

В задачах всё это так проявляется: велосипедист за «2 часа, а потом 3 часа» проедет 2 + 3 * 15 километров. Всего хватает и сомнений выражение не вызывает.

Лига Педагогов

1.1K постов 4.7K подписчика

Правила сообщества

Писать все, что можно отнести к педагогам и педагогике.

3. Оскорблять участников сообщества;

4. Писать не по теме;

Вы перегрузили ребенку понятие скобок. Слишком много шелухи, и он путается.

Затем вводим скобки, как ограничитель части выражения и чётким безусловным требованием выполнить сначала все действия во всех скобках.

Отдайте его на курсы программирования на языке LISP.

Тогда он навсегда запомнит скобки.

Интересно, в других языках нашей группы такой конструкт, как я выше написал, возможен? 🙂

Кстати, запись вида (-5) я где-то видел. Но, скорее всего, в каком-то языке программирования так операнды записываются. Хм.

А, и да: я вот что-то не помню, чтобы нам приходилось текстовую форму задачи приводить в математический вид такой сложности записи.
Всегда поэтапно шли: разбили-вычленили из условия подзадачи. Прорешали каждую.
И уже в самом конце интегрировали в единое уравнение или пример.

Или я заблуждаюсь, что современная программа образования скорее призвана отуплять, нежели учить интегрировать информацию?

Добиваться понимания пока что уровень примеров позволяет. Что в итого выльется в *жопочасы*. Просто искра понимания на простейшие манипуляции вспыхивала через год-полтора спонтанно.

Хотя на моей памяти скобки не могут являться проблемой. Что там у нас из самых опасных вариантов? Четные степени и. Все?

В дробях действие с числителем подразумевается автоматически, в записи многочленов на слух? Там обычно прлизносится *скобка открывается, пять плюс два, закрывается*.

Ну логично же ответил

Олимпиада по математике 3 класс

Что такое вектор в математике?

Сегодня на занятии мы определим, что такое вектор, каких видов он бывает и разберёмся, как совершать действия с векторами.

Что и как у нас устроено внутри?

Поговорим про расположение внутренних органов, изучим систему органов и их анатомический состав, рассмотрим уровни организации структур в организме.

Подобные треугольники

Сегодня мы вспомним, что такое подобне треугольники и по каким признакам понять, что они подобны.

Ответ MefistiK в «Перемена мест слагаемых»

Ответ на пост «Перемена мест слагаемых»

Ответ orlik09 в «Школа, чтоб её. »

Ответ на пост «Школа, чтоб её. »

Ответ на пост «Школа, чтоб её. »

Тем не менее, после 9 класса школы пошел в техникум (поступил благодаря подготовительным курсам, где фактически разжевывались те же задачи, что потом были на экзамене).

На собрании цикловой комиссии, где составлялись списки на отчисление, в списки попал и я.

И тогда, из по-моему 40 человек с потока, которых собирались отчислять, пятерым, кото не был замечен в тяжких грехах, разрешили сдать математику в 6-й раз.

Преподаватель завел нас в кабинет, написал на доске три задачи (простых даже для меня, типа «а дважды два случайно не четыре?»), и вышел из кабинета на сорок минут. Потом пришел, собрал исписанные листочки, не глядя в них бросил в мусорное ведро, и поставил тройки в зачетки. В итоге я доучился: на сессиях больше проблем не было, несмотря на «гуманитарный» склад ума, т.к. у одного из немногих у меня дома компьютер (94-98 года), и по многим вещам у меня знаний было больше, чем у преподавателей.

Также из примерно 30 человек был в числе 15, кто после получения «компьютерной» специальности в техникуме пошел в университет (к сожалению, тоже технический), и даже получил высшее образование. И, насколько мне известно, из тех же двух групп выпуска 1998 года я единственный, кто успешно связал свою жизнь с ИТ-сферой.

Школа, чтоб её.

В 9й класс я пошла в новую школу.

При подаче документов, мамочка просила определить меня в простой класс. Уже всё было понятно: дочь гуманитарий глубоких глубин.. русский, литература, английский и вот это всё. Физика-химия-алгебра не ложится совсем. Два-три стабильно. При ретроградном Меркурии были иногда четвёрки. И, благодаря жертвоприношениям Старым Богам, я таки наскребла на четвёрку в году за 8й класс.

Мест в простом классе не нашлось, и завуч с гордостью предложила математический класс.

Классрук покивала, успокоила мамочку и заверила, что ежели детка не будет создавать дисциплинарных проблем, то пусть переписывает учебник, заодно и труды Макрса, Энгельса и Ленина. На том и порешили.

Первую неделю сентября я отходила отлично: новый класс, знакомства, новые учителя. Всё прекрасно. 1го числа курили с новой подружкой за школой..ээх..веселье.

Я не понимала такое поведение: ведь мамочка попросила её не трогать меня. Дисциплину я не нарушала, приходила вовремя, сидела молча. Что ещё надо?

Много позже я поняла всю глубину несчастья этой женщины: одинокая, живущая с мамой. живущая только работой и своим предметом. Она никак не могла понять и поверить, что кому-то алгебра на самом деле совсем не нужна.

В 11м классе на выпускном она мне сказала, что посмотрит куда я поступлю с таким аттестатом: алгебра 3, геометрия 3, физика 3. До ЕГЭ ещё жить и жить было, а иняз меня прекрасно принял на бюджет.

И вот в 2021м году я вспомнила, как стояла тогда перед доской, на которой было написано log (логарифм). И всё, что было в моей голове это то, что log по английски это бревно.

Источник

Раскрытие скобок

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:

Первое правило раскрытия скобок

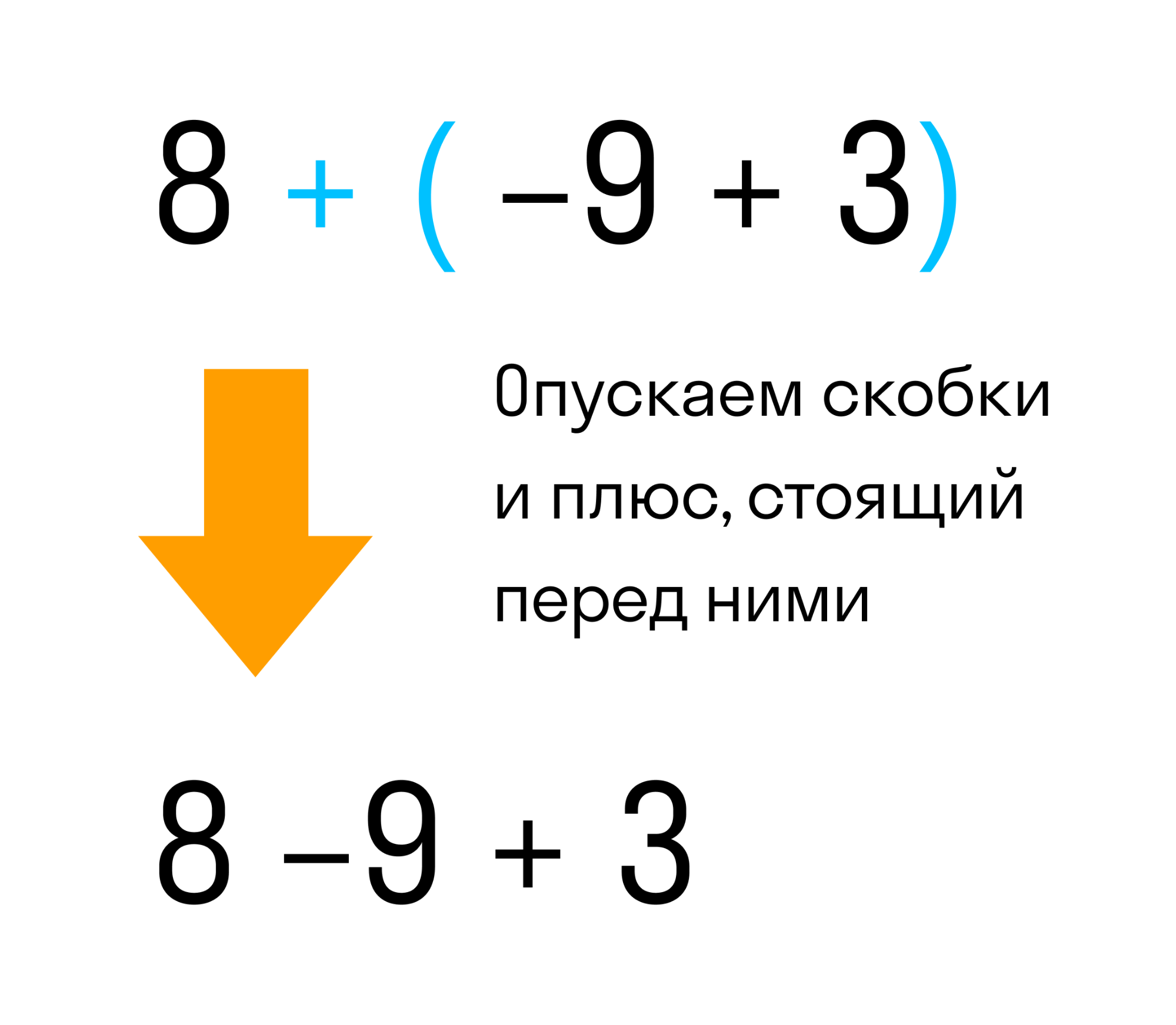
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок

Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.

Формула раскрытия скобок

Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Перед скобками стоит плюс, значит применим то же правило:

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

Пример 4. Раскрыть скобки в выражении (−7)

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок

Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.

Формула раскрытия скобок

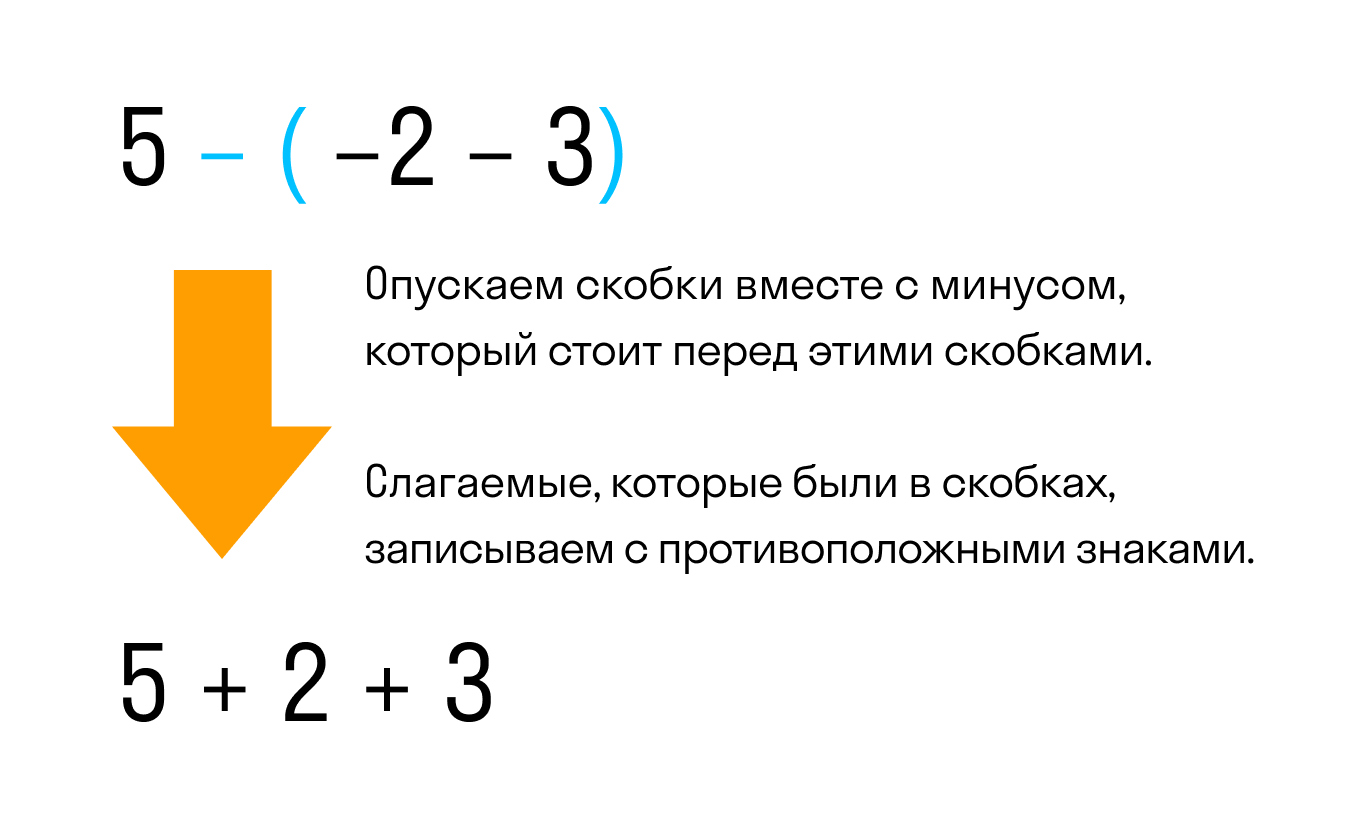
Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 2. Раскрыть скобки −(−6 + 7)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Другие правила раскрытия скобок

Правило раскрытия скобок при делении

Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.

Формула раскрытия скобок

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:

Далее умножим скобку на число:

Правило раскрытия скобок при умножении:

Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.

Формула раскрытия скобок

Пример 1. Раскрыть скобки 5(3 − x)

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Таблица с формулами раскрытия скобок

Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.

Правила раскрытия круглых скобок вида (-a), в которых находится одночлен

Правила раскрытия круглых скобок, в которых находится многочлен

Скобки убирают, знаки всех слагаемых в скобках не меняют, если:

Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:

Раскрытие круглых скобок при умножении одночлена на многочлен

Раскрытие круглых скобок при умножении многочлена на многочлен

Раскрытие круглых скобок при возведении многочлена в степень

(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2

Скобка в скобке

В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:

Чтобы успешно решать подобные задания, нужно:

При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.

Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))

Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.

Теперь раскроем вторую скобку, внешнюю:

Упростим получившееся выражение:

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

Пример 1. Раскрыть скобки и упростить выражение:

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Задачи для самостоятельного решения

На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.

Задание 6. Раскройте скобки:

Задание 7. Раскройте скобки:

Источник